Кинематика. Решение задач

1. КИНЕМАТИКА

Решение задач

2. УСЛОВИЕ ЗАДАЧИ

Движение точки М задано уравнениями:
,
х f1 t 2 t
y f2 t t 2
х и у выражены в сантиметрах, t – в секундах.
Найти уравнение траектории, скорость и
ускорение точки в момент времени

3. Движение точки, заданное координатным способом, происходит в плоскости Оху. Для определения уравнения траектории выразим время

t из
уравнения движения вдоль оси х.
x
t 0
2
и подставив в уравнение движения по оси у, получим
x2
y
4
Следовательно, траекторией точки является ветвь параболы
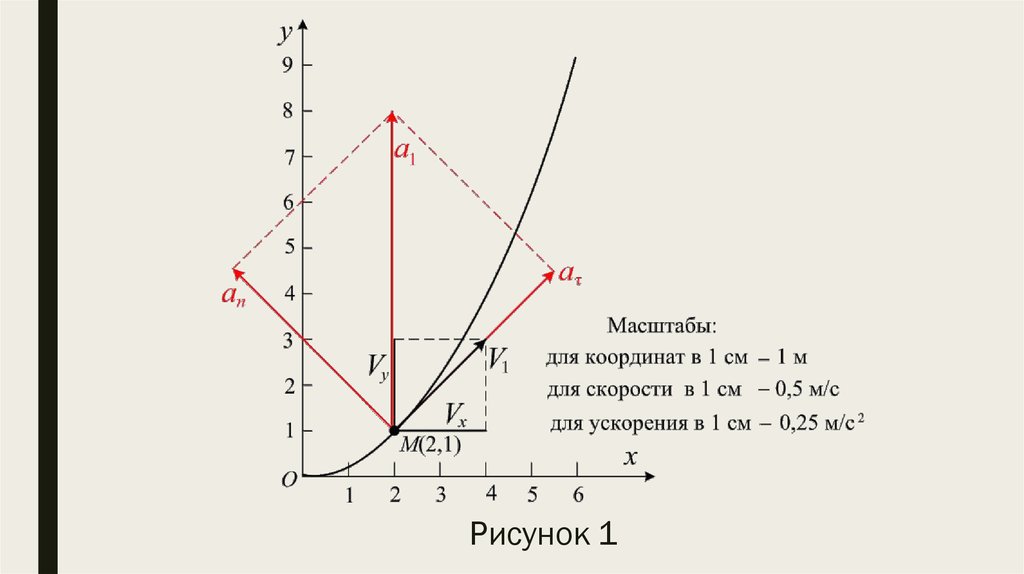
(рисунок 1) при x ≥ 0.
В момент времени t = 1 с точка находится в положении М(2,1)

4. Рисунок 1

5. Вычислим проекции скорости и ускорения точки на декартовые оси при t = 1 с

dx d 2 t
Vx
2м / с
dt
dt
2
dy d t
Vy
2 t 2 1 2 м / с
dt
dt
dVx d 2
2
ax
0м / с
dt
dt
dV y d 2 t
2
ay
2м / с
dt
dt

6. Тогда в декартовой системе координат векторы скорости и ускорения точки равны. Найдем их модули.

V1 Vx2 V y2 2 2 м / с
а1 a x2 a 2y 2 м 2 / с
Определим направления векторов по формулам
Vx
2
cos V 1 i
V1
2
ax
cos a1 i
0
a1
r
1
r
1
cos V
cos a
r
r
a
j
j
Vy
2
V1
2
ay
1
0

7. Следовательно, вектор скорости образует с осями Ох и Oу углы, равные 45°, а вектор ускорения точки М направлен вдоль оси Oу.

Поскольку точка М движется по кривой, то вектор её ускорения
разложим на касательное ускорение и нормальное ускорение.
Определим касательное ускорение точки в момент времени 1 c.
Vx a x V y a y 0 4
2
a
2м / с
V
2 2
Вычислим нормальное ускорение точки в этот момент
времени
aп а а 2
2
2
2
2
2
2 м / с2

8. Тогда в данном положении точки радиус кривизны траектории равен

2 2
V
ап
2
2
1
2
5,64 м / с
ЗАДАЧА РЕШЕНА
2

9. УСЛОВИЕ ЗАДАЧИ

Точка В движется в плоскости ху. Закон движения точки
задан уравнениями
,
t
х f1 t 6 cos
6
t
y f 2 t 4 sin
6
2
х и у выражены в сантиметрах, t – в секундах.
Найти уравнение траектории точки; для момента
времени t1 = 1 c определить скорость и ускорение точки,
а также ее касательное и нормальное ускорения и
радиус кривизны в соответствующей точке траектории.
.

10. Для определения уравнения траектории точки исключим из заданных уравнений движения времени t

t
х 8 cos
6
t
х 8 cos 6
t
x 2 cos2
6
2
t
y 4 sin
6
2
t
y 4 1 cos
6
t
y 4 4 cos2
6
2
t
x cos
6
2
2
y 4
2 t
cos
4
6
y 4
2
x
4
x2 4 y 4
4 x2 4 y

11. Скорость точки найдем по ее проекциям на координатные оси

dx
t
6
t
t
t
vх
6 cos
sin
6 sin
sin
dt
6
6
6 6
6
6
1
v х sin
1,57см / с
6
dy
t
t
t 4
t
2
vy
4 sin
sin
4 2 sin
cos
dt
6
6
6
6
6
3
4
1
vy
sin
1,81см / с
6
3
v v х v y 1,57 1,81 2,396 2, 4см / с
2
2
2
2

12. Аналогично находим ускорение точки

2
t
dv х
t
sin
aх
cos
6
dt
6
6
2
t
2
с
/
см
4
1,
1,396
a х cos
6
6
2 2
4
t
t
cos
sin
ay
9
dt 6
3
3
2 2
1
2
cos
ay
1,095см / с
9
3
dv y
a aх a y
2
2
1, 4
2
1,095 1,77см / с
2
2

13. Определяем касательное ускорение

1,57 1, 4 1,81 1,095
a
0,11см / с 2
2, 4
Определяем нормальное ускорение
an a a 1,77 0,11 1,766см / с 2
2
2
2
2
Определяем радиус кривизны траектории
v 2 2, 42
3, 262см
an 1,766

14. ЗАДАЧА РЕШЕНА