Кинематика материальной точки. (Тема 1)

1. ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ ИНЖЕНЕРНО-ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ, ТАГАНРОГ

ФИЗИКА
ОБЩИЙ КУРС

2. ЛИТЕРАТУРА

1. Савельев И.В. Курс общей физики.
2. Уколов А.С. Лекции по общему курсу
физики ч. 1-5. Заичкин Н.Н. ч. 6-7.
3. Трофимова Т.И. Курс физики.
4. Учебно-методическое пособие для
выполнения индивидуального задания
по дисциплине «Физика». №4956-1,2,3.
5. Сивухин Д.В.; Матвеев А.Н.;
Фейнман Р.Ф.

3.

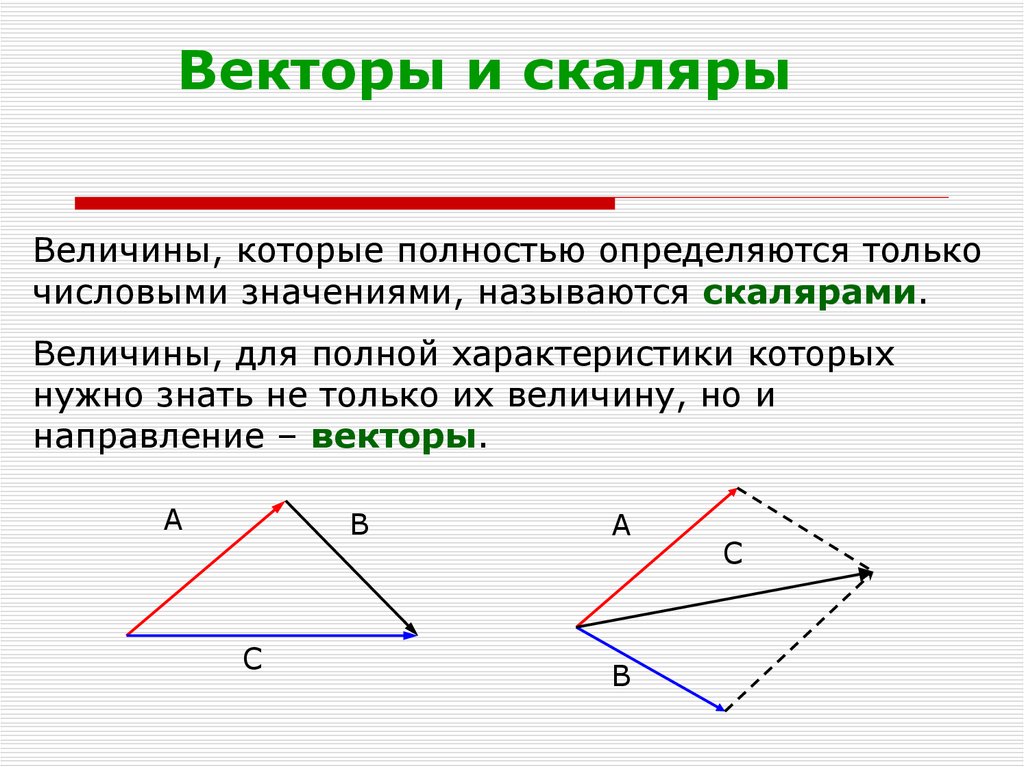
Векторы и скаляры
Величины, которые полностью определяются только
числовыми значениями, называются скалярами.
Величины, для полной характеристики которых
нужно знать не только их величину, но и
направление – векторы.
А
В
С
А
В
С

4.

Скалярное произведение векторов -скаляр
a
(a b ) | a | | b | cos
α
b
Векторное произведение векторов - вектор
[a b ] | a | | b | sin
a
b
[a b ]
[b a ]
b
a

5. ТЕМА I. КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ

§1. Основные понятия кинематики

6. 1.МЕХАНИЧЕСКАЯ СИСТЕМА

Механической системой называется любой
объект (набор объектов), механическим
движением которого мы интересуемся.

7. 2. МАТЕРИАЛЬНАЯ ТОЧКА

Тело, размерами которого в условиях данной
задачи можно пренебречь, называется
материальной точкой (частицей).

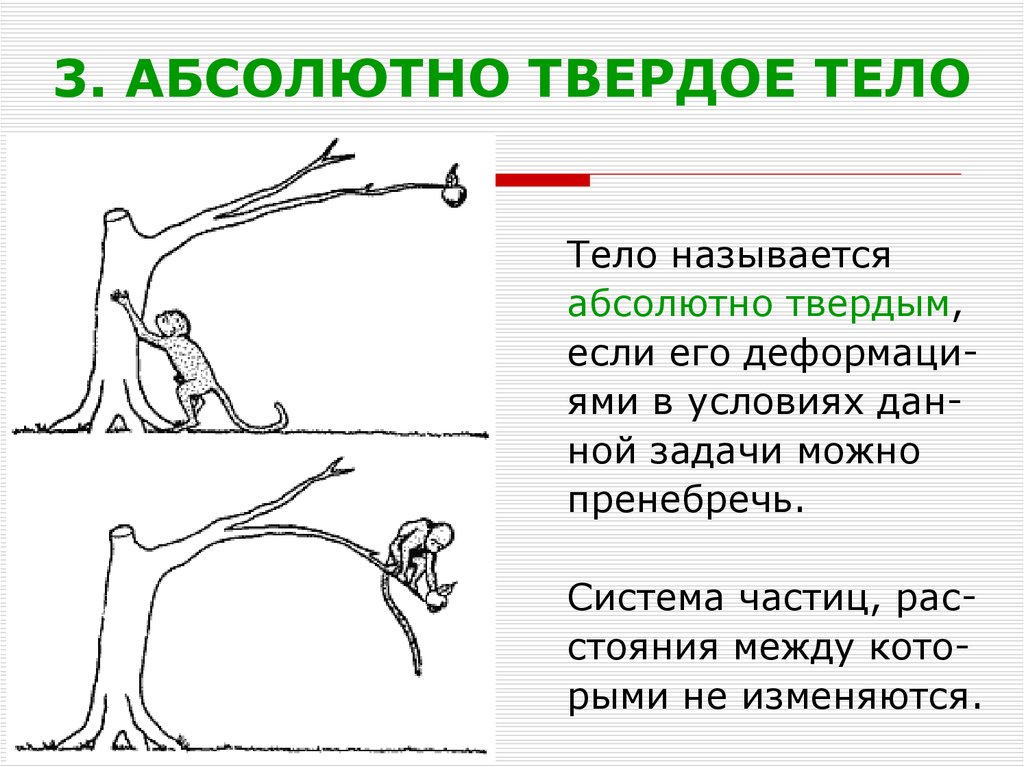
8. 3. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО

Тело называется
абсолютно твердым,
если его деформациями в условиях данной задачи можно
пренебречь.
Система частиц, расстояния между которыми не изменяются.

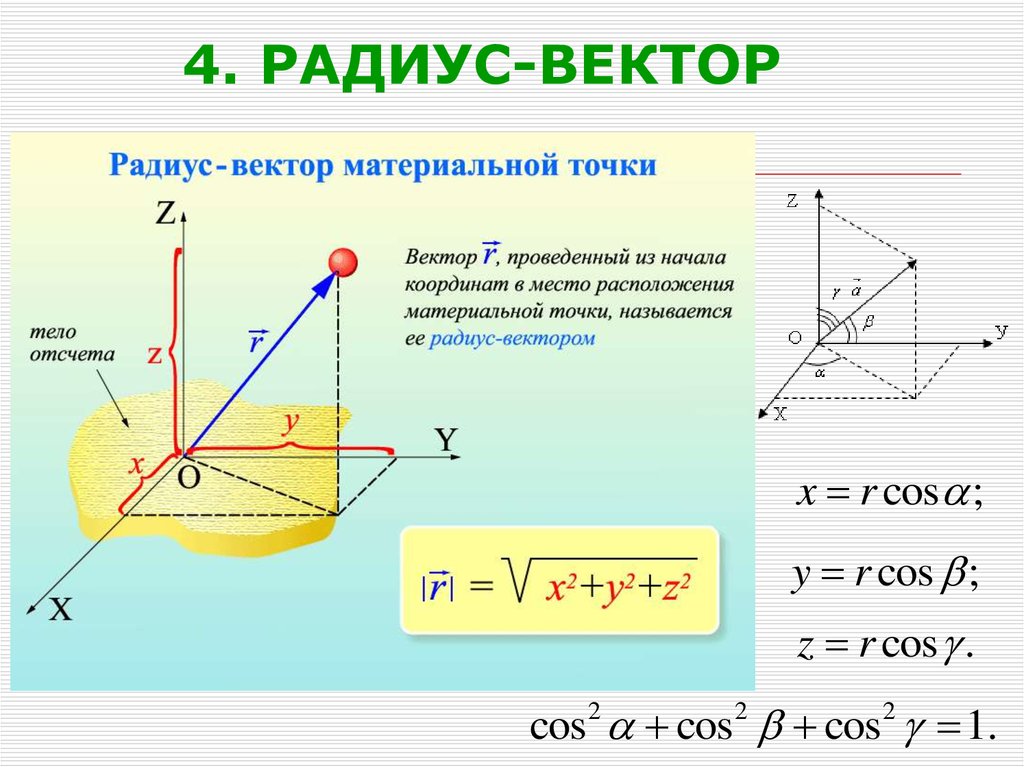
9. 4. РАДИУС-ВЕКТОР

x r cos ;
y r cos ;
z r cos .
cos2 cos2 cos2 1.

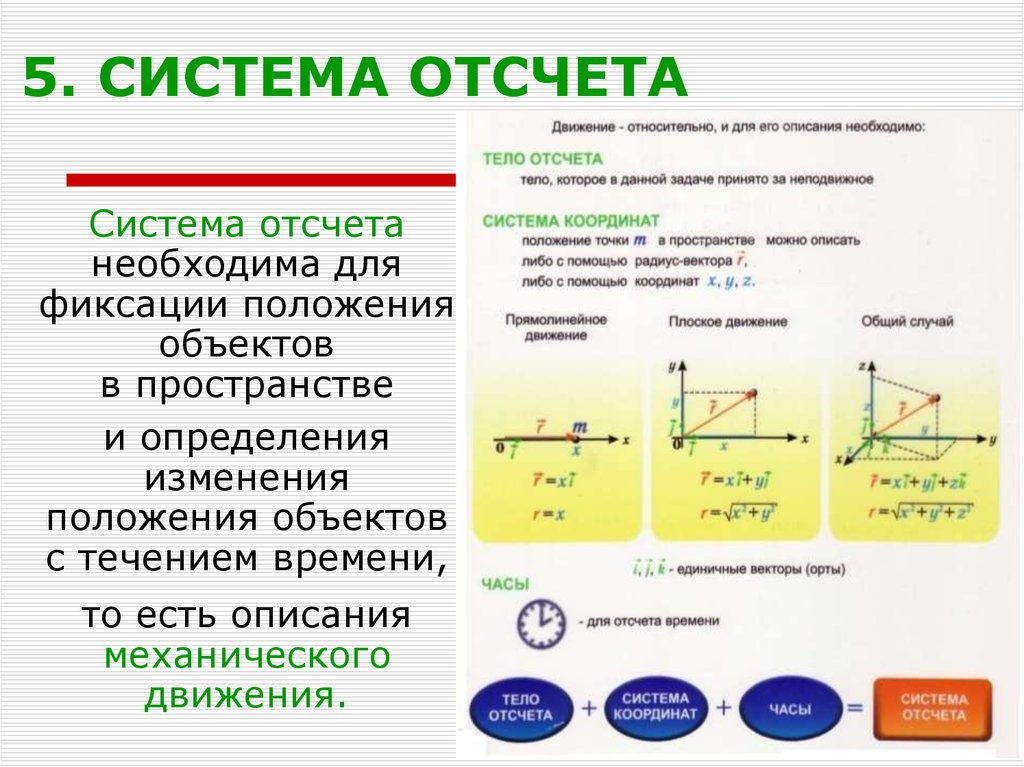
10. 5. СИСТЕМА ОТСЧЕТА

Система отсчета
необходима для
фиксации положения
объектов
в пространстве
и определения
изменения
положения объектов
с течением времени,
то есть описания
механического
движения.

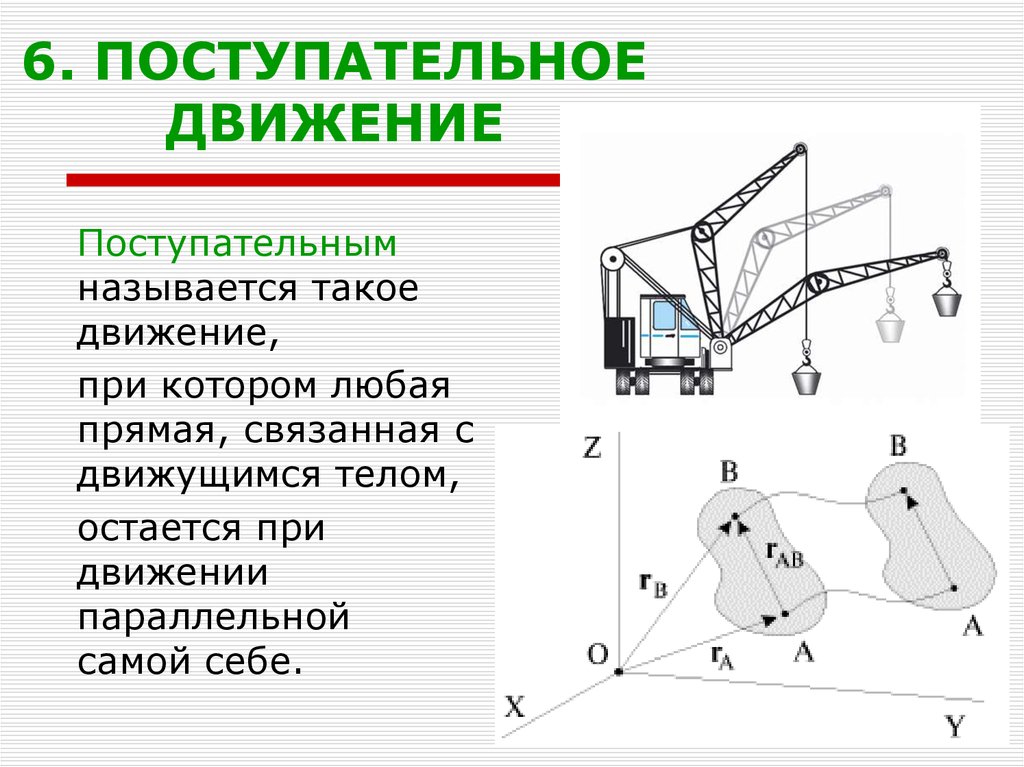
11. 6. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ

Поступательным
называется такое
движение,
при котором любая
прямая, связанная с
движущимся телом,
остается при
движении
параллельной
самой себе.

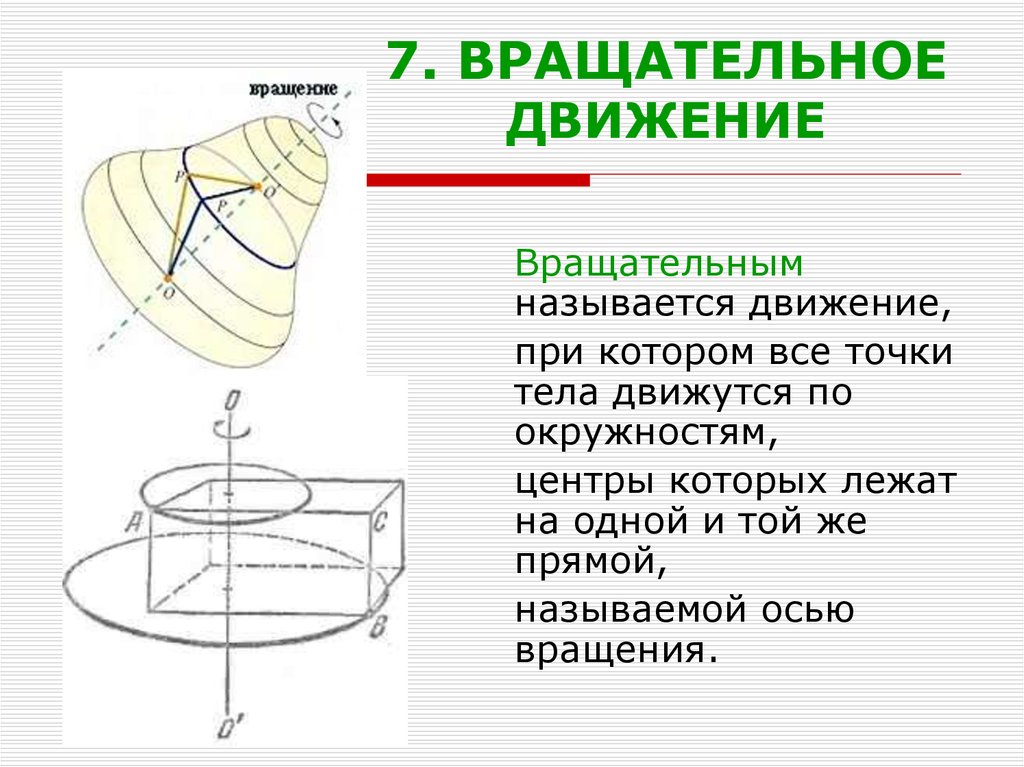
12. 7. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ

Вращательным
называется движение,
при котором все точки
тела движутся по
окружностям,
центры которых лежат
на одной и той же
прямой,
называемой осью
вращения.

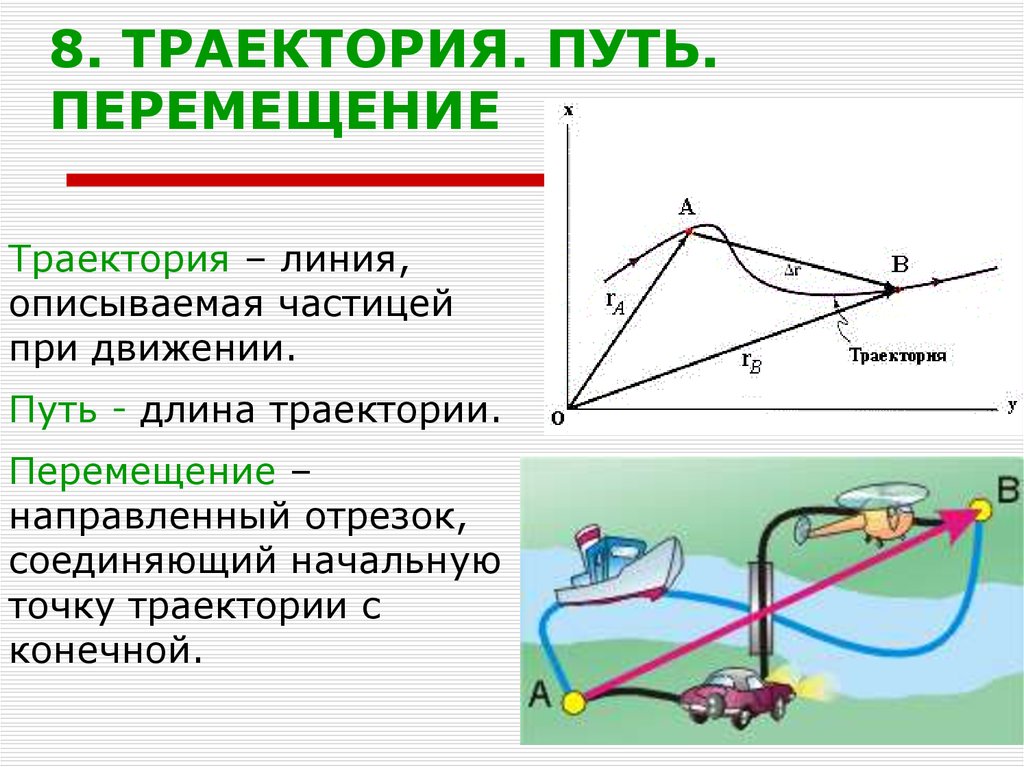
13. 8. ТРАЕКТОРИЯ. ПУТЬ. ПЕРЕМЕЩЕНИЕ

Траектория – линия,
описываемая частицей
при движении.
Путь - длина траектории.
Перемещение –
направленный отрезок,
соединяющий начальную
точку траектории с
конечной.

14. § 2. СКОРОСТЬ

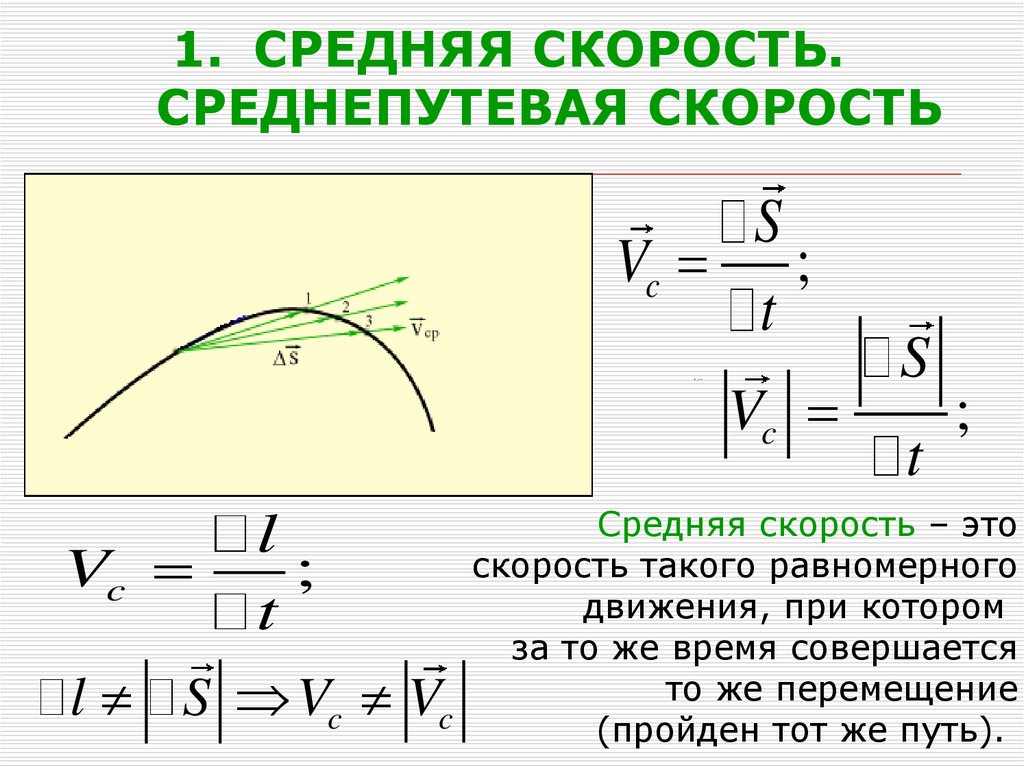
15. СРЕДНЯЯ СКОРОСТЬ. СРЕДНЕПУТЕВАЯ СКОРОСТЬ

1. СРЕДНЯЯ СКОРОСТЬ.
СРЕДНЕПУТЕВАЯ СКОРОСТЬ
S
Vc ;
t
Vc
Vc
l
;
t
l S Vc
Vc
S
t
;
Средняя скорость – это
скорость такого равномерного
движения, при котором
за то же время совершается
то же перемещение
Vc
(пройден тот же путь).

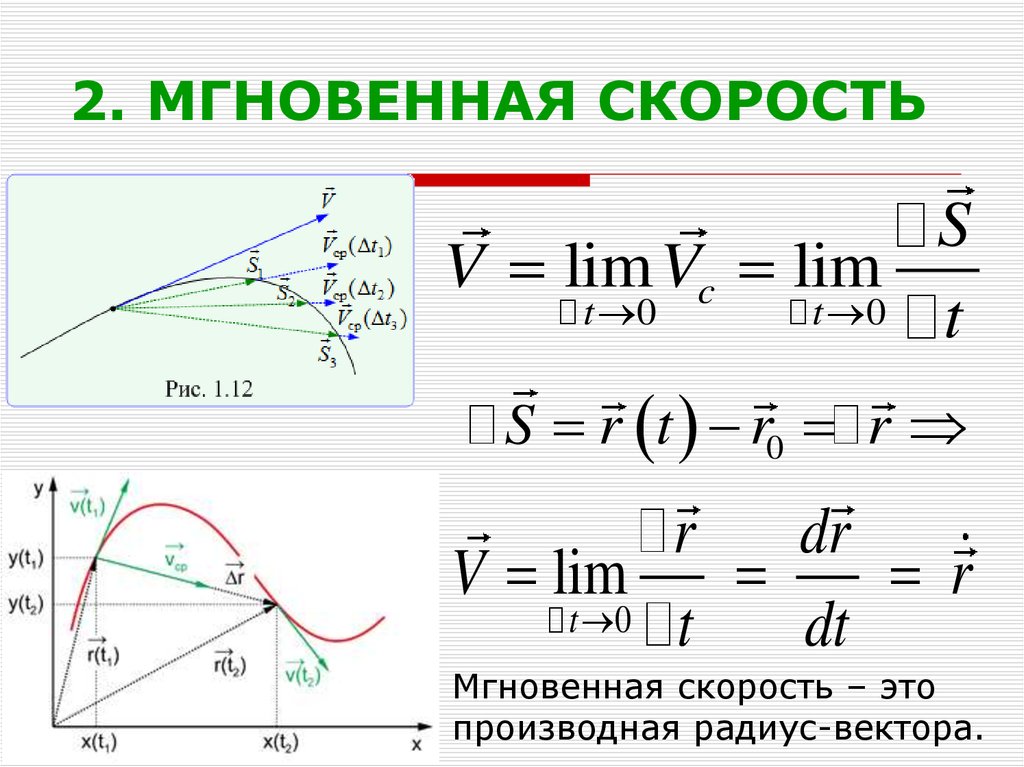
16. 2. МГНОВЕННАЯ СКОРОСТЬ

S
V lim Vc lim
t 0
t 0
t
S r t r0 r
r
dr
V lim
r
t 0 t
dt
Мгновенная скорость – это
производная радиус-вектора.

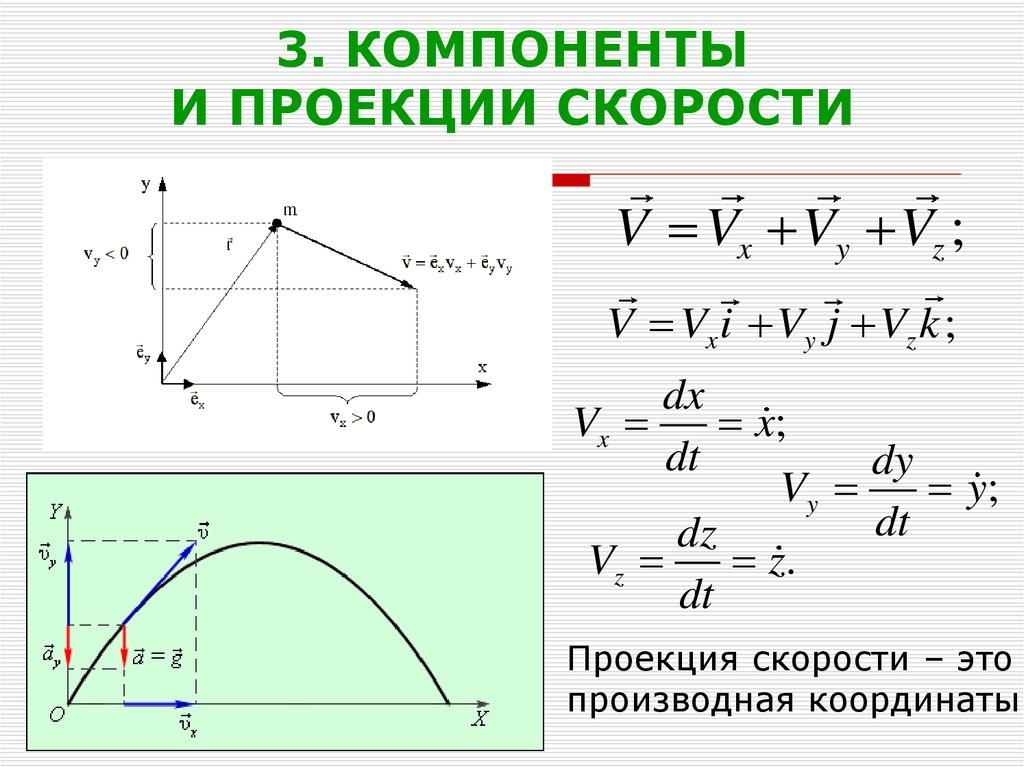
17. 3. КОМПОНЕНТЫ И ПРОЕКЦИИ СКОРОСТИ

V Vx Vy Vz ;
V Vx i Vy j Vz k ;
dx
Vx
x;
dt
dy
Vy
y;
dt
dz
Vz
z.
dt
Проекция скорости – это
производная координаты.

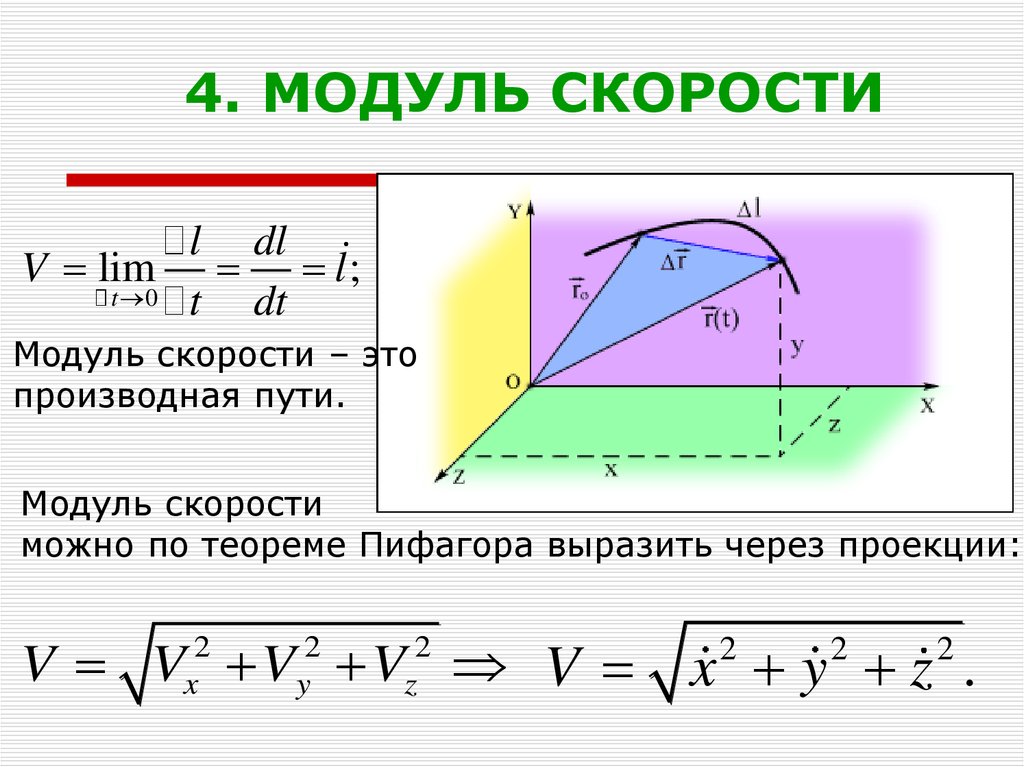
18. 4. МОДУЛЬ СКОРОСТИ

l dl
V lim l ;
t 0 t
dt
Модуль скорости – это
производная пути.
Модуль скорости
можно по теореме Пифагора выразить через проекции:
V V V V V
2
x
2
y
2
z
x y z .
2
2
2

19. 5. ЗАКОН ДВИЖЕНИЯ

Закон движения – это уравнение,
определяющее положение тела в
пространстве в любой момент времени.
r (t ) r0 S (t );
t
dS Vdt S Vdt.
0
x(t ) x0 S x (t ),
y (t ) y0 S y (t ),
z (t ) z0 S z (t ).
t
dS x Vx dt S x Vx dt...
0

20. 6. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ

Прямолинейное равномерное
движение – это такое движение,
при котором скорость тела
постоянна по величине
и направлению:
x
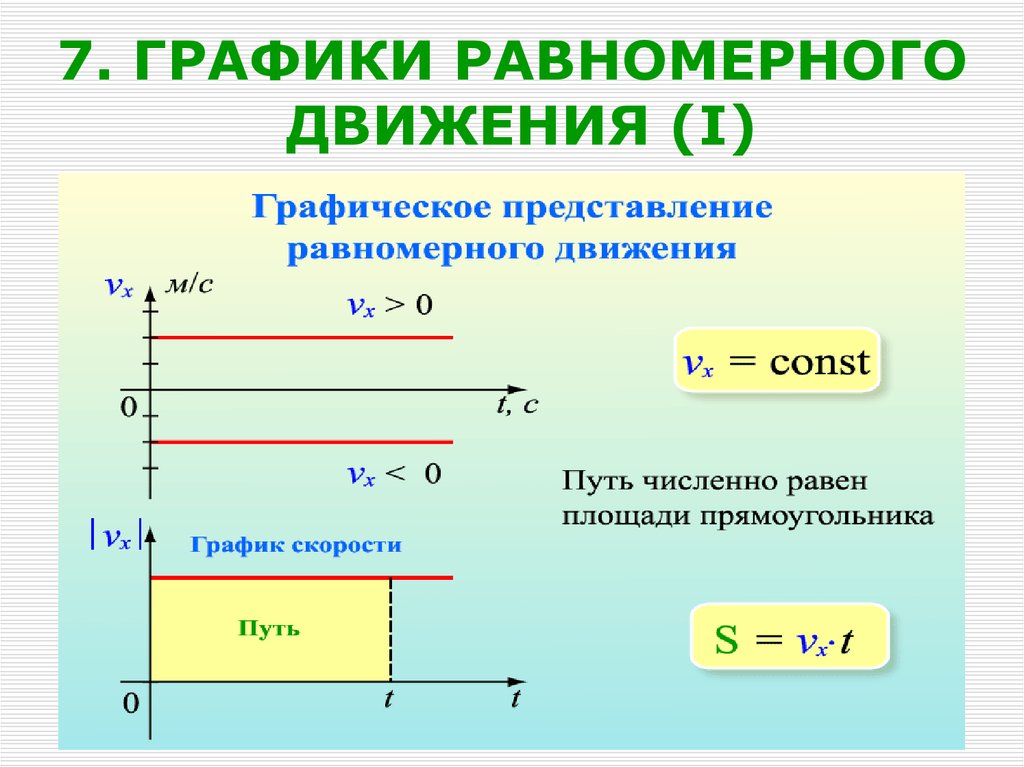
V const.
S x Vx t;
x(t ) x0 S x (t );
x(t ) x0 Vx t.

21. 7. ГРАФИКИ РАВНОМЕРНОГО ДВИЖЕНИЯ (I)

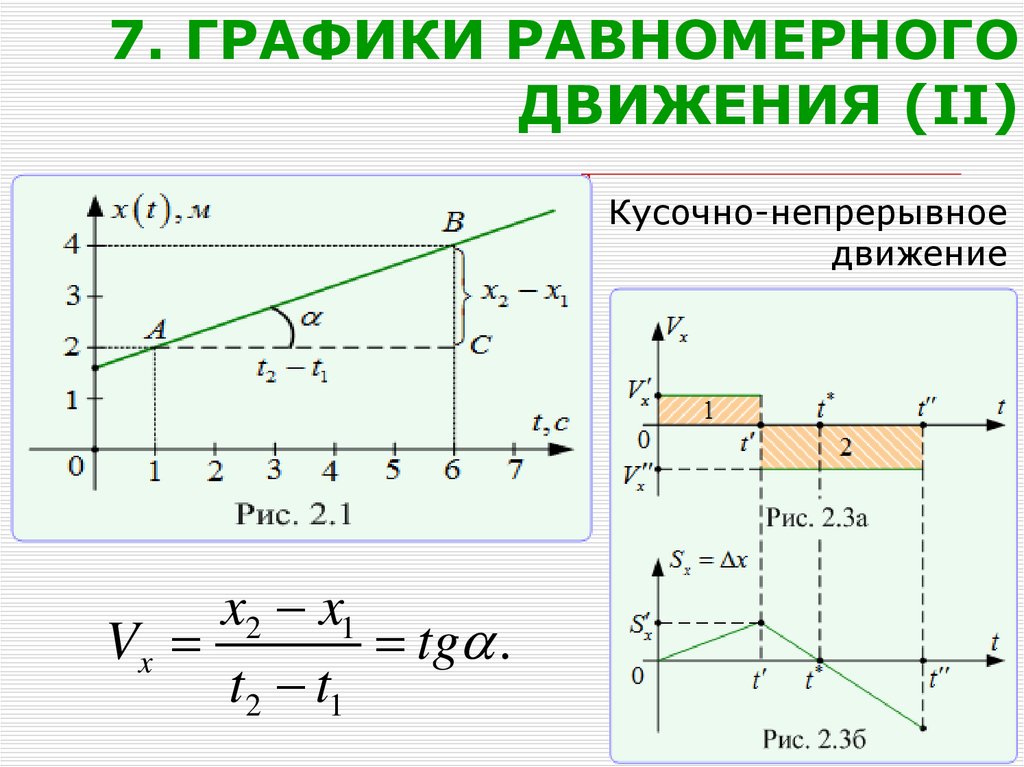
22. 7. ГРАФИКИ РАВНОМЕРНОГО ДВИЖЕНИЯ (II)

Кусочно-непрерывное
движение
x2 x1
Vx
tg .
t2 t1

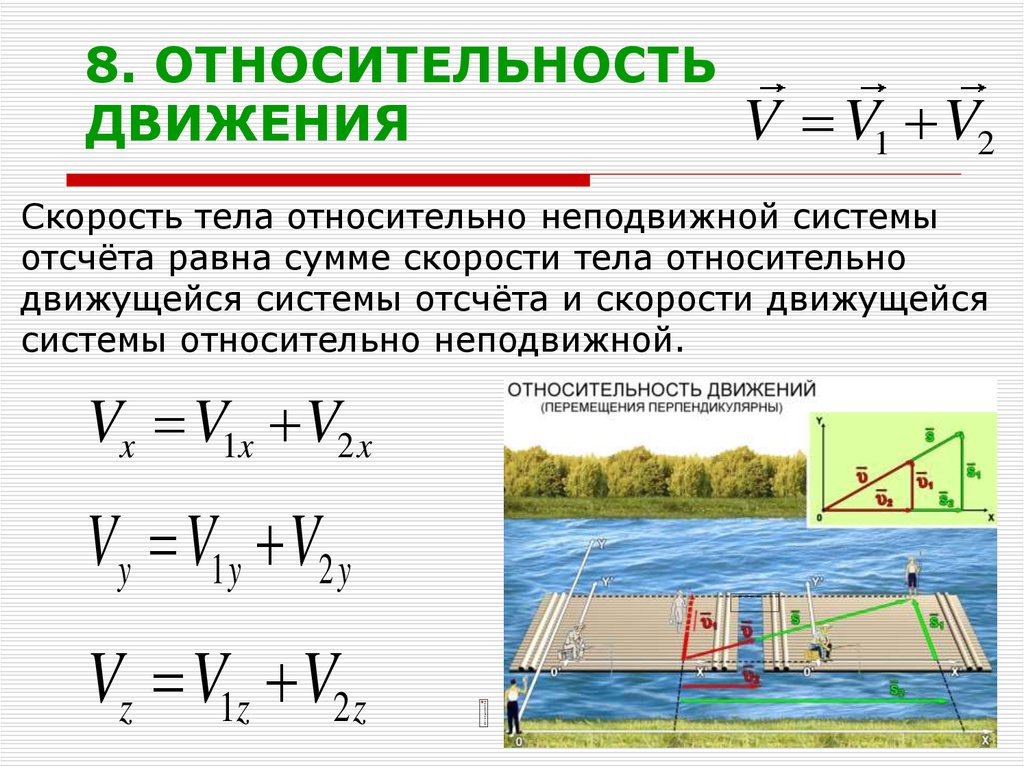
23. 8. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ

V V1 V2
Скорость тела относительно неподвижной системы
отсчёта равна сумме скорости тела относительно
движущейся системы отсчёта и скорости движущейся
системы относительно неподвижной.
Vx V1x V2 x
Vy V1 y V2 y
Vz V1z V2 z

24. §3. УСКОРЕНИЕ

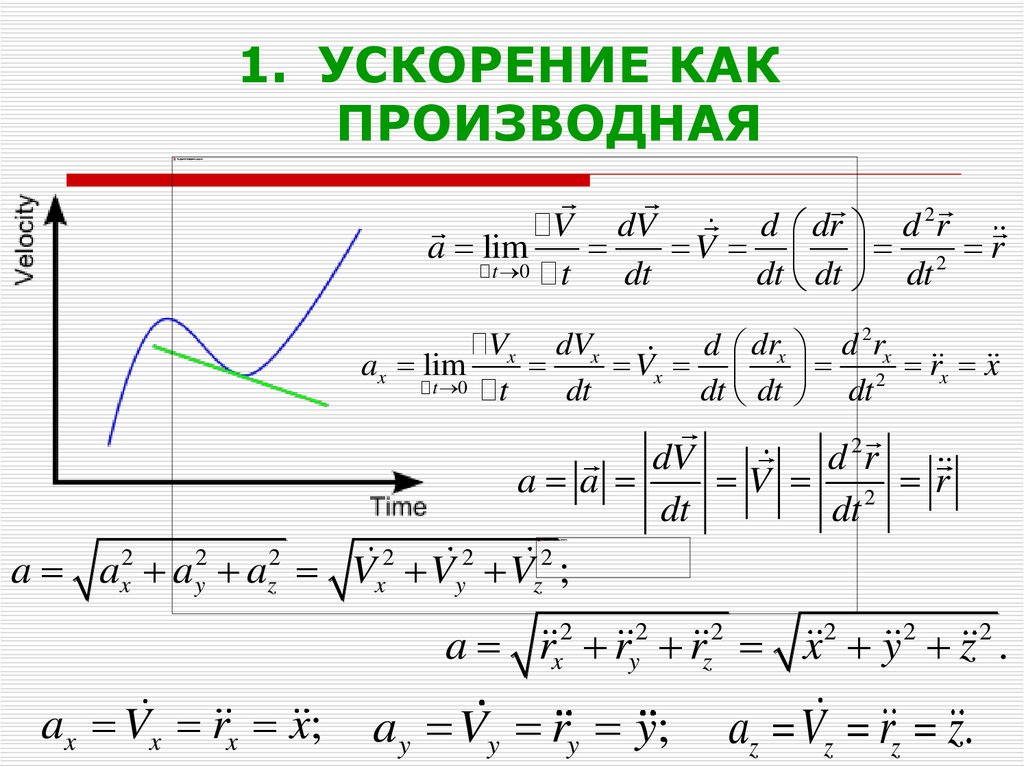
25. УСКОРЕНИЕ КАК ПРОИЗВОДНАЯ

1. УСКОРЕНИЕ КАК
ПРОИЗВОДНАЯ
V dV
d dr d 2 r
a lim
V 2 r
t 0
t
dt
dt dt dt
Vx dVx
d drx d 2 rx
ax lim
Vx
2 rx x
t 0
t
dt
dt dt dt
dV
d 2r
a a
V 2 r
dt
dt
a ax2 a y2 az2 Vx2 Vy2 Vz2 ;
a rx2 ry2 rz2 x 2 y 2 z 2 .
ax Vx rx x;
ay Vy ry y;
az Vz rz z.

26. 2. ЕСТЕСТВЕННЫЕ КОМПОНЕНТЫ УСКОРЕНИЯ

V V ;
n ;
n 1;
V V Vn ;
V V Vn n;
V
V
Vn
a lim
lim
lim
n
t 0
t 0
t
t t 0 t
V
Vn
a lim
n lim
a an ;
t 0
t 0
t
t
d
dV
d
a V
V
a an ;
dt
dt
dt

27. 3. ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ

Тангенциальное ускорение характеризует
изменение скорости по величине.
a 0;
a a ;
dV
a
V;
dt
a 0;
dV
a
V ;
dt

28. 4. НОРМАЛЬНОЕ УСКОРЕНИЕ

Нормальное ускорение характеризует
изменение скорости по направлению.
V const V 2V sin 2 ;
2V
an a lim sin
;
t 0
2
t
t 0 0 sin 2 2
an lim V
V lim
V ;
t 0
t 0
t
t
V V an V ;

29. 5. КРИВИЗНА ТРАЕКТОРИИ

Кривизна траектории
количественная характеристика
кривой линии.
1
d
C lim
lim
;
S 0 S
R S 0 S
dS
S
an lim V
V lim
t 0
t 0
t
S t
S V
an V lim
lim
.
S 0
S t 0 t R
2

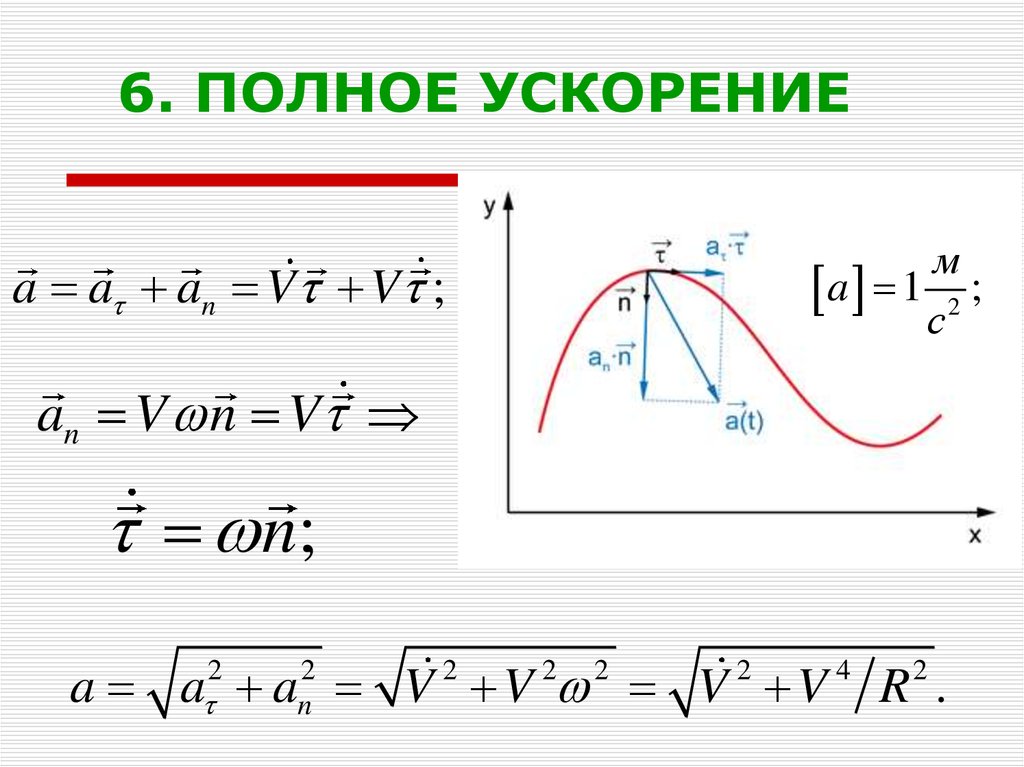
30. 6. ПОЛНОЕ УСКОРЕНИЕ

м
a 1 2 ;
с
a a an V V ;
an V n V
n;
a a a V V V V
2
2
n
2
2
2
2
4
2
R .

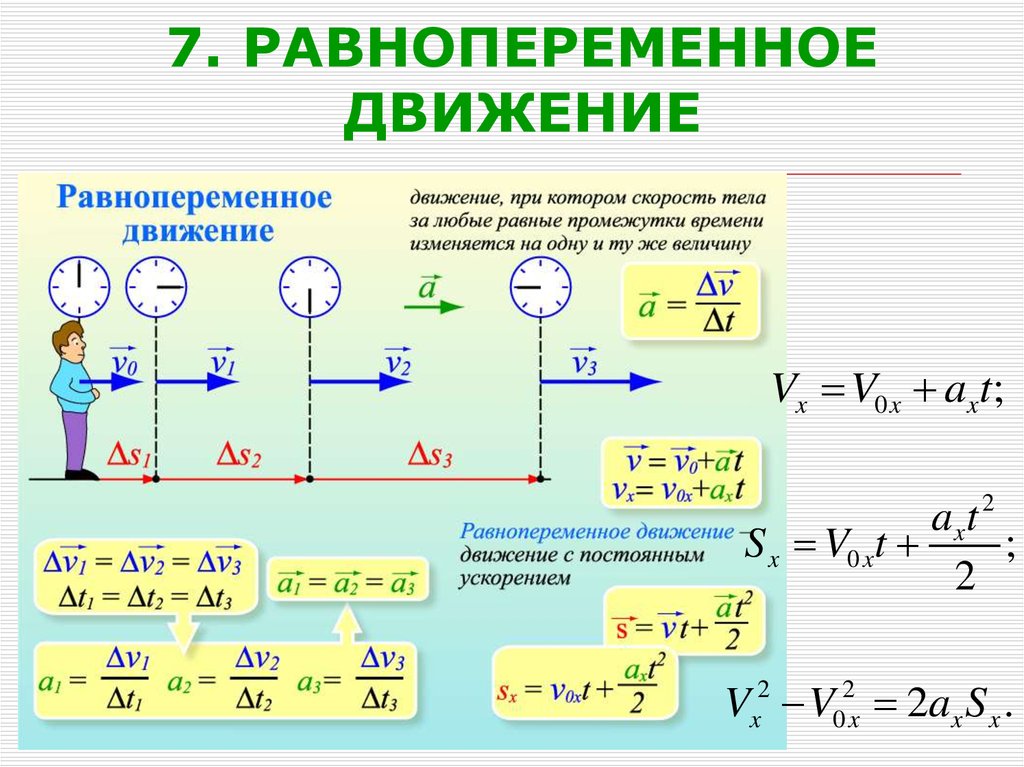
31. 7. РАВНОПЕРЕМЕННОЕ ДВИЖЕНИЕ

Vx V0 x axt;
2
axt
S x V0 xt
;
2
Vx2 V02x 2ax S x .

32. 8. ГРАФИКИ РАВНОПЕРЕМЕННОГО ДВИЖЕНИЯ

Vx V0 at;
axt 2
S x V0 xt
;
2
ax 2
V0 x
Sx t 2
t ;
2
ax
ax 2
V0 x V02x V02x
Sx t 2
t 2 2 ;
2
ax
ax ax
ax 2
V0 x V02x V02x
Sx t 2
t 2
;
2
ax
a x 2a x
2
ax V0 x V02x
Sx t
.
2
a x 2a x
Vx V0 at;

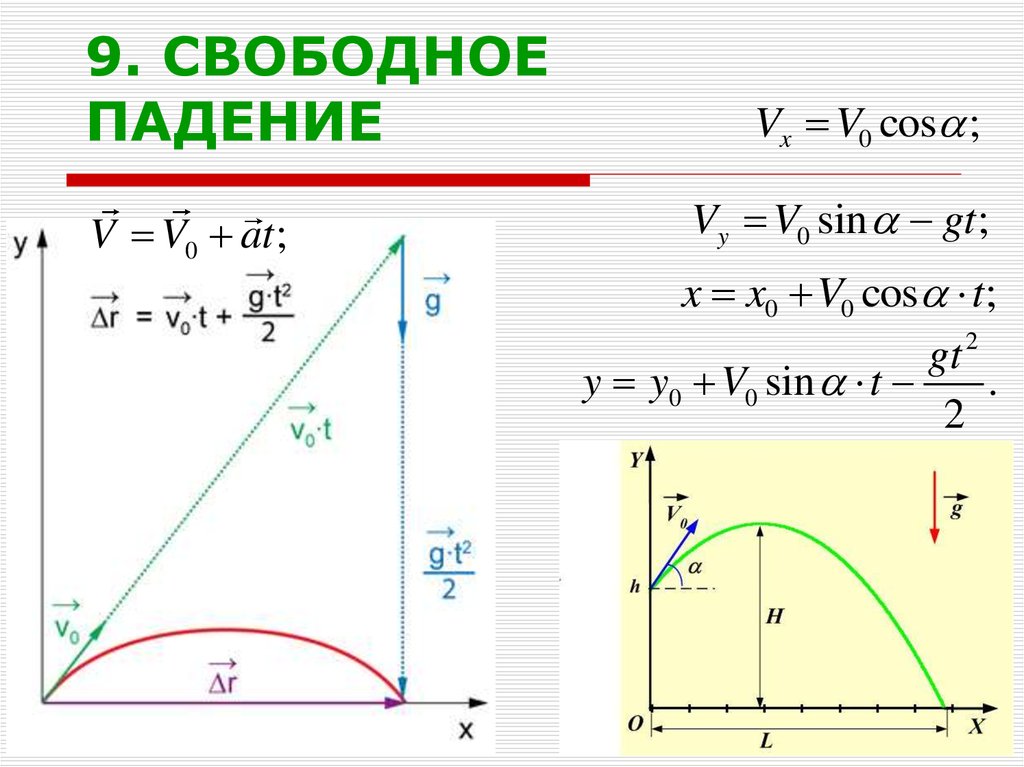
33. 9. СВОБОДНОЕ ПАДЕНИЕ

V V0 at ;
Vx V0 cos ;
Vy V0 sin gt ;
x x0 V0 cos t;
gt 2
y y0 V0 sin t
.
2

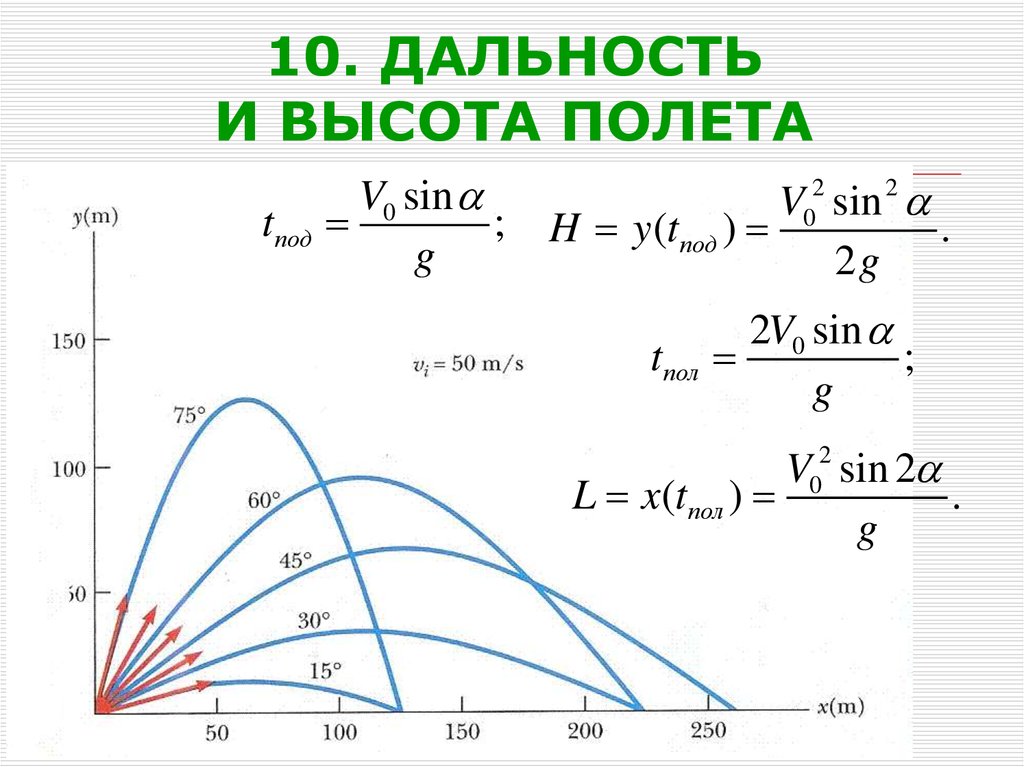
34. 10. ДАЛЬНОСТЬ И ВЫСОТА ПОЛЕТА

tпод
V0 sin
;
g
V02 sin 2
H y (tпод )
.
2g
tпол
2V0 sin
;
g
V02 sin 2
L x(tпол )
.
g

35. §4. КИНЕМАТИКА ДВИЖЕНИЯ ПО ОКРУЖНОСТИ

36. 1. ПЕРИОД И ЧАСТОТА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

dt
2 R
T
; T
;
dN
V
dN
1
;
dt
T
T 1c; 1c
1
1Гц;

37. 2. РАВНОМЕРНОЕ ВРАЩЕНИЕ

2
;
t
T
2 ;
рад
1 ;
с

38. 3. РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЕ

d
;
dt
d z
z z
;
dt
z ;
рад
1 2 .
с

39. 4. УГЛОВАЯ И ЛИНЕЙНАЯ СКОРОСТИ

dl d
V
;
dt
dt
r sin V r sin ;
r r sin ;
V r
V r ;

40. 5. УГЛОВОЕ И ЛИНЕЙНОЕ УСКОРЕНИЯ

an V R 2 R;
dV d
a
z R
dt dt
d z
a R
R z ;
dt
d
d
r
d
V
d
a
r a r r V ;
dt dt
dt dt
2
a r ;
an V r r r ;

41.

Классификация движения
в зависимости от тангенциальной и нормальной
составляющих ускорения
прямолинейное равномерное
движение
прямолинейное равноускоренное
движение
прямолинейное движение с
переменным ускорением;
равномерное движение по
окружности
равномерное криволинейное
движение
криволинейное равноускоренное
движение
криволинейное движение с
переменным ускорением

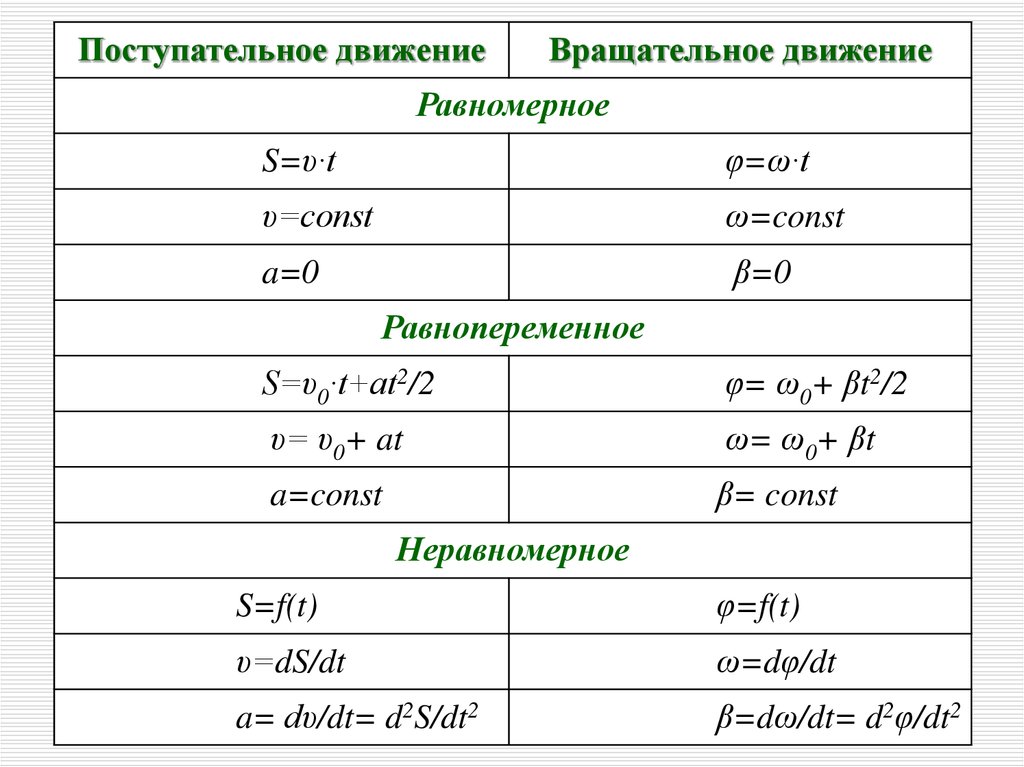
42.

Поступательное движение
Вращательное движение
Равномерное
S=υ·t
φ=ω·t
υ=const
ω=const
a=0
β=0
Равнопеременное
S=υ0·t+at2/2
φ= ω0+ βt2/2
υ= υ0+ at
ω= ω0+ βt
a=const
β= const
Неравномерное
S=f(t)
φ=f(t)
υ=dS/dt
ω=dφ/dt
a= dυ/dt= d2S/dt2
β=dω/dt= d2φ/dt2