Similar presentations:
Кинематика материальной точки. Тема №1
1. ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ ИНЖЕНЕРНО-ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ
ФИЗИКАдоцент И.Б. Доценко
кафедра физики ИНЭП
Email: ibdocenko@sfedu.ru
2. ЛИТЕРАТУРА
1. Савельев И.В. Курс общей физики.2. Уколов А.С. Лекции по общему курсу
физики ч. 1-5. Заичкин Н.Н. ч. 6-7.
3. Трофимова Т.И. Курс физики.
4. Учебно-методическое пособие для
выполнения индивидуального задания
по дисциплине «Физика». №4956-1,2,3.
5. Иродов И.Е.;
Матвеев А.Н.;
Сивухин Д.В.;
Фейнман Р.Ф.
3. ТЕМА I. КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ
§1. Основные понятия кинематики4. 1.МЕХАНИЧЕСКАЯ СИСТЕМА
Механической системой называется любойобъект (набор объектов), механическим
движением которого мы интересуемся.
5. 2. МАТЕРИАЛЬНАЯ ТОЧКА
Тело, размерами которого в условиях даннойзадачи можно пренебречь, называется
материальной точкой (частицей).
6. 3. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО
Тело называетсяабсолютно твердым,
если его деформациями
в условиях данной
задачи можно
пренебречь.
Абсолютно твёрдое
тело – это система
частиц, расстояния
между которыми не
изменяются.
7. 4. СИСТЕМА ОТСЧЕТА
Система отсчета определяет положение частиц в пространствеи изменение этого положения с течением времени (часы).
Тело отсчёта считается
условно неподвижным.
Система координат ”
привязана” к телу отсчёта.
Выбор системы координат зависит
от типа движения: прямолинейного, плоского,
объёмного; и от симметрии движения:
полярная,
цилиндрическая,
сферическая.
8. 5. РАДИУС-ВЕКТОР
Проекции радиус-вектора частицы на координатные осиопределяют положение этой частицы (её координаты):
x r cos ;
Теорема о направляющих косинусах:
cos2 cos2 cos2 1.
y r cos ;
z r cos .
9. 6. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
Поступательнымназывается такое движение,
при котором любая прямая,
связанная с движущимся телом,
остается при движении
параллельной самой себе.
При поступательном движении
все точки тела движутся одинаково:
1. Одинаковая траектория.
2. Одинаковая скорость.
3. Одинаковое ускорение.
10. 7. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
Вращательнымназывается такое движение,
при котором все точки твёрдого
тела движутся по окружностям,
находящимся в параллельных
плоскостях.
Центры этих окружностей лежат
на одной и той же прямой,
называемой осью вращения.
Если ось вращения находится
вне тела, то говорят что оно
совершает круговое движение.
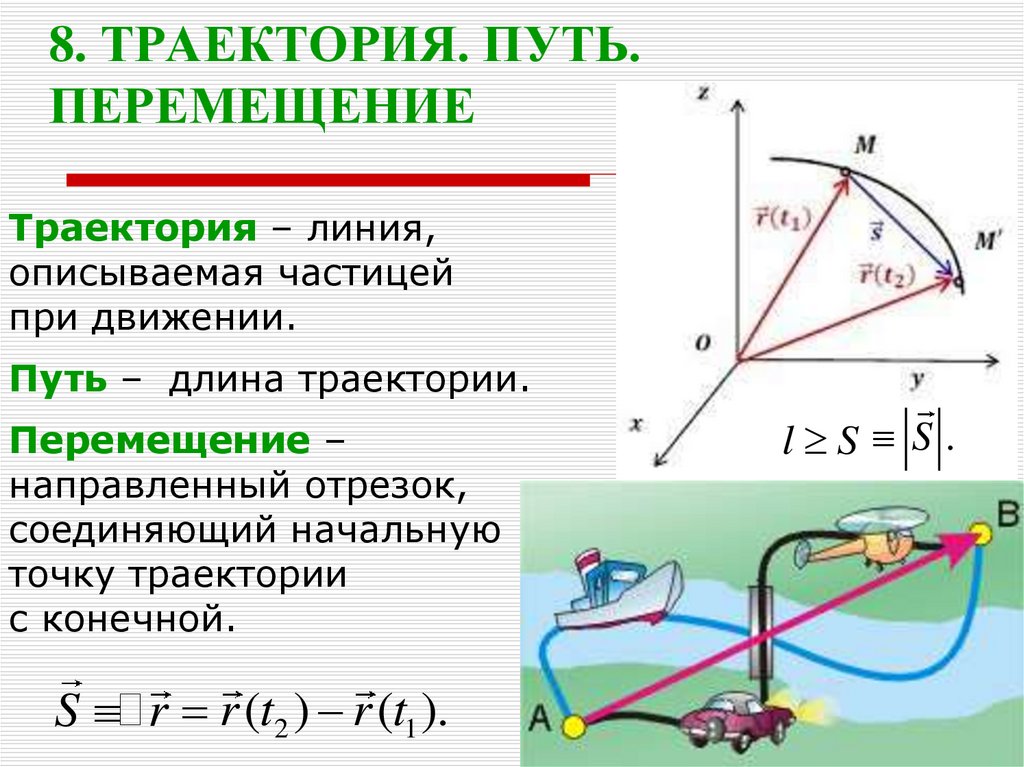
11. 8. ТРАЕКТОРИЯ. ПУТЬ. ПЕРЕМЕЩЕНИЕ
Траектория – линия,описываемая частицей
при движении.
Путь – длина траектории.
Перемещение –
направленный отрезок,
соединяющий начальную
точку траектории
с конечной.
S r r (t2 ) r (t1 ).
l S S .
12. § 2. СКОРОСТЬ
13. 1. СРЕДНЯЯ СКОРОСТЬ. СРЕДНЕПУТЕВАЯ СКОРОСТЬ
VcS
t
.
Средняя скорость – это
скорость такого равномерного
движения, при котором
за то же время совершается
то же перемещение
Vc
S
Vc ;
t
На замкнутой траектории
Vc 0.
На практике используется среднепутевая скорость
(среднее значение модуля скорости) – это скорость
l
такого равномерного движения, при котором
Vc
.
за то же время будет пройден тот же путь
t
Т. к. пройденный путь не равен модулю перемещения
l S , то величины этих скоростей не равны: Vc Vc .
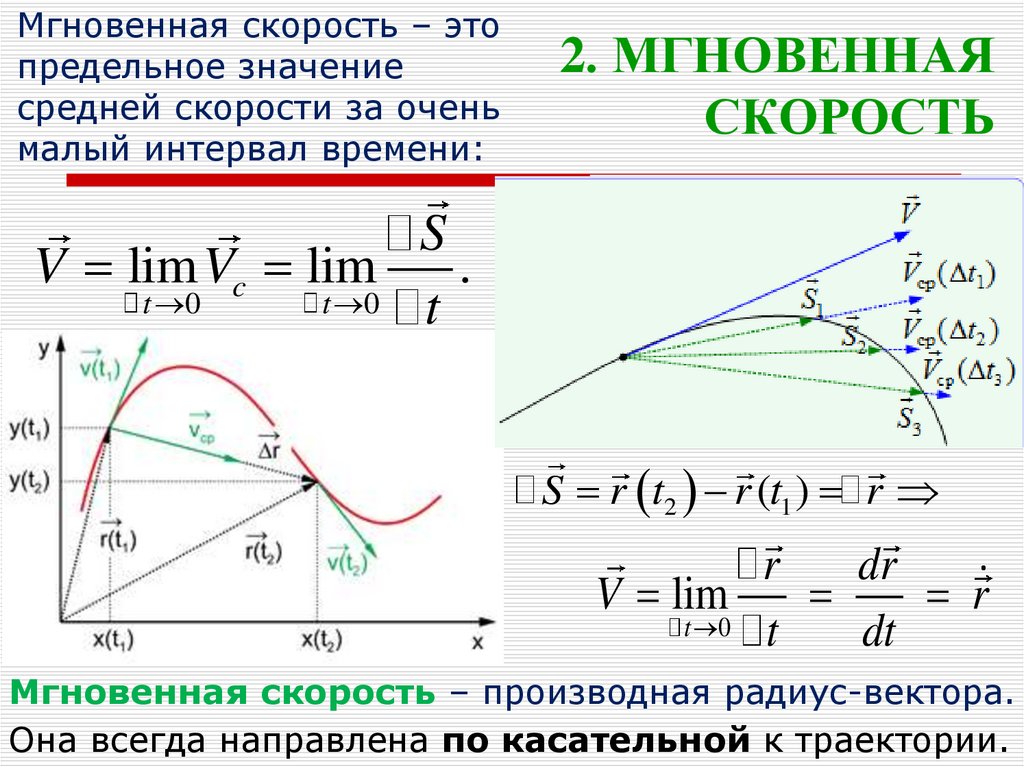
14. 2. МГНОВЕННАЯ СКОРОСТЬ
Мгновенная скорость – этопредельное значение
средней скорости за очень
малый интервал времени:
2. МГНОВЕННАЯ
СКОРОСТЬ
S
V lim Vc lim
.
t 0
t 0
t
S r t2 r (t1 ) r
r
dr
V lim
r
t 0 t
dt
Мгновенная скорость – производная радиус-вектора.
Она всегда направлена по касательной к траектории.
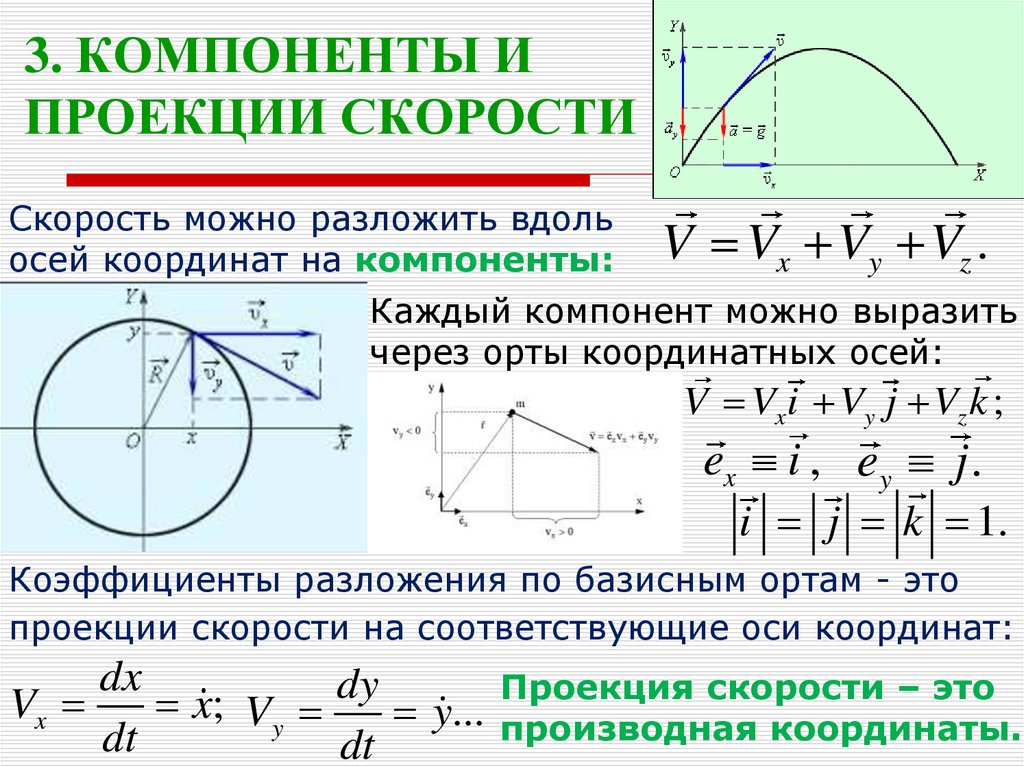
15. 3. КОМПОНЕНТЫ И ПРОЕКЦИИ СКОРОСТИ
Скорость можно разложить вдольосей координат на компоненты:
V Vx Vy Vz .
Каждый компонент можно выразить
через орты координатных осей:
V Vx i Vy j Vz k ;
ex i , ey j .
i j k 1.
Коэффициенты разложения по базисным ортам - это
проекции скорости на соответствующие оси координат:
dx
Vx
x; Vy dy y...
dt
dt
Проекция скорости – это
производная координаты.
16. 4. МОДУЛЬ СКОРОСТИ
l dlV lim l ;
t 0 t
dt
Модуль скорости – это
производная пути.
Модуль скорости
можно по теореме Пифагора выразить через проекции:
V V V V V
2
x
2
y
2
z
x y z .
2
2
2
17. 5. ЗАКОН ДВИЖЕНИЯ
Закон движения – это уравнение,определяющее положение тела в
пространстве в любой момент времени.
r (t ) r0 S (t );
t
dS Vdt S Vdt.
0
x(t ) x0 S x (t ),
y (t ) y0 S y (t ),
z (t ) z0 S z (t ).
t
dS x Vx dt S x Vx dt...
0
18. 6. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
Прямолинейное равномерноедвижение – это такое движение,
при котором скорость тела
постоянна по величине
и направлению:
x
V const.
S x Vx t;
x(t ) x0 S x (t );
x(t ) x0 Vx t.
19. 7. ГРАФИКИ РАВНОМЕРНОГО ДВИЖЕНИЯ (I)
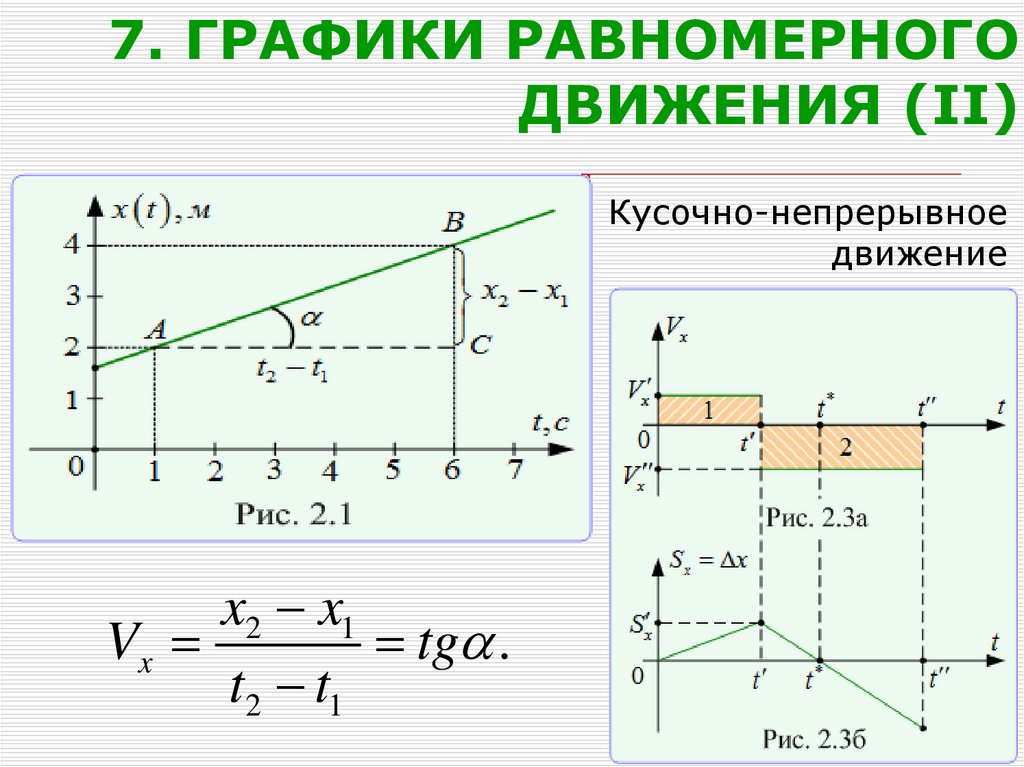
20. 7. ГРАФИКИ РАВНОМЕРНОГО ДВИЖЕНИЯ (II)
Кусочно-непрерывноедвижение
x2 x1
Vx
tg .
t2 t1
21. 8. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
V V1 V2Скорость тела относительно неподвижной системы
отсчёта равна сумме скорости тела относительно
движущейся системы отсчёта и скорости движущейся
системы относительно неподвижной.
Vx V1x V2 x
Vy V1 y V2 y
Vz V1z V2 z
22. §3. УСКОРЕНИЕ
23. УСКОРЕНИЕ КАК ПРОИЗВОДНАЯ
1. УСКОРЕНИЕ КАКПРОИЗВОДНАЯ
V dV
d dr d 2 r
a lim
V 2 r
t 0
t
dt
dt dt dt
Vx dVx
d drx d 2 rx
ax lim
Vx
2 rx x
t 0
t
dt
dt dt dt
dV
d 2r
a a
V 2 r
dt
dt
a ax2 a y2 az2 Vx2 Vy2 Vz2 ;
a rx2 ry2 rz2 x 2 y 2 z 2 .
ax Vx rx x;
ay Vy ry y;
az Vz rz z.
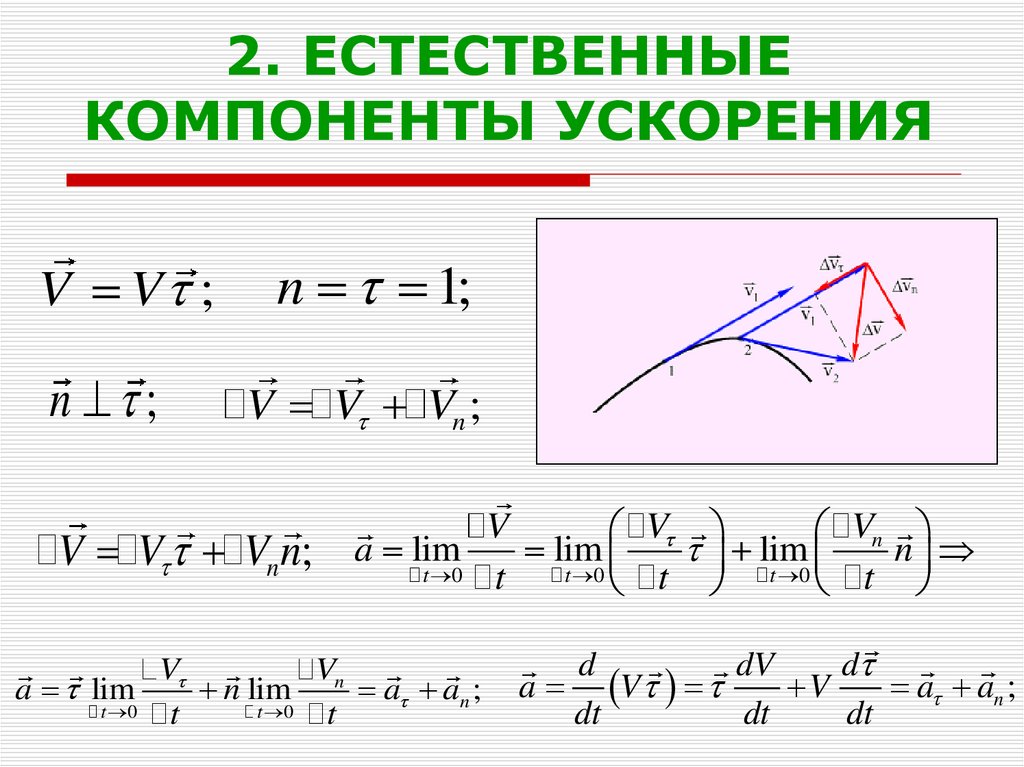
24. 2. ЕСТЕСТВЕННЫЕ КОМПОНЕНТЫ УСКОРЕНИЯ
V V ;n ;
n 1;
V V Vn ;
V V Vn n;
V
V
Vn
a lim
lim
lim
n
t 0
t 0
t
t t 0 t
V
V
a lim n lim n a an ;
t 0
t 0
t
t
d
dV
d
a V
V
a an ;
dt
dt
dt
25. 3. ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ
Тангенциальное ускорение характеризуетизменение скорости по величине.
a 0;
a a ;
dV
a
V;
dt
a 0;
dV
a
V ;
dt
26. 4. НОРМАЛЬНОЕ УСКОРЕНИЕ
Нормальное ускорение характеризуетизменение скорости по направлению.
V const V 2V sin 2 ;
2V
an a lim sin
;
t 0
2
t
t 0 0 sin 2 2
an lim V
V lim
V ;
t 0
t 0
t
t
V V an V ;
27. 5. КРИВИЗНА ТРАЕКТОРИИ
Кривизна траекторииколичественная характеристика
кривой линии.
1
d
C lim
lim
;
S 0 S
R S 0 S
dS
S
an lim V
V lim
t 0
t 0
t
S t
S V
an V lim
lim
.
S 0
S t 0 t R
2
28. 6. ПОЛНОЕ УСКОРЕНИЕ
мa 1 2 ;
с
a a an V V ;
an V n V
n;
a a a V V V V
2
2
n
2
2
2
2
4
2
R .
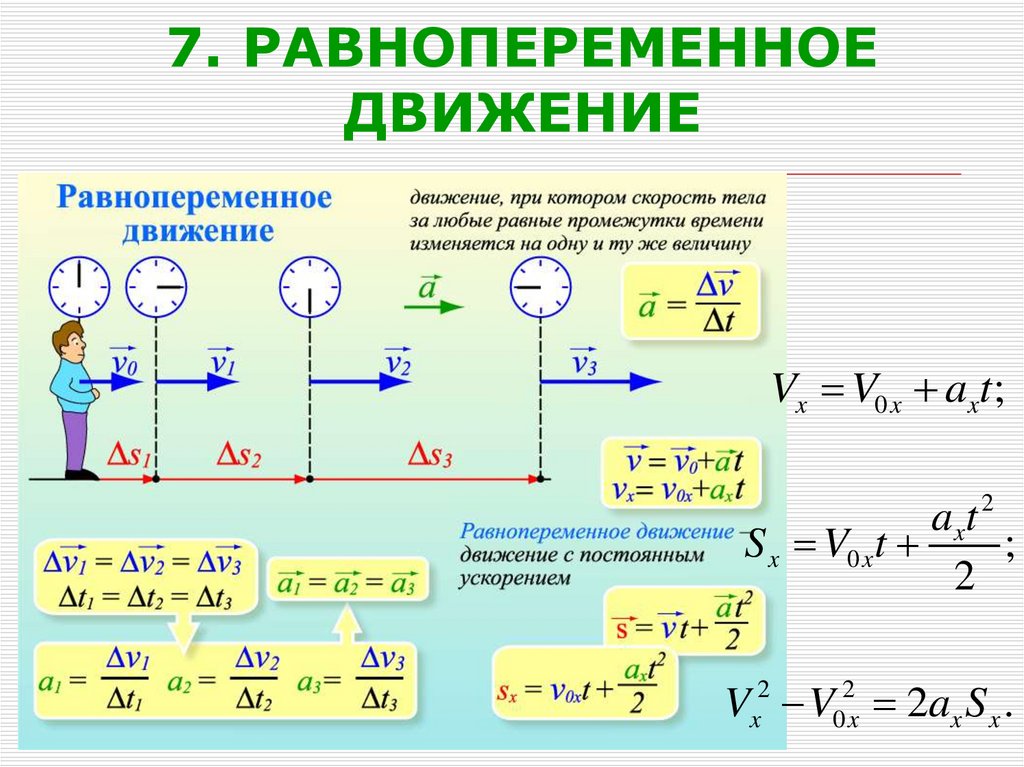
29. 7. РАВНОПЕРЕМЕННОЕ ДВИЖЕНИЕ
Vx V0 x axt;2
axt
S x V0 xt
;
2
Vx2 V02x 2ax S x .
30. 8. ГРАФИКИ РАВНОПЕРЕМЕННОГО ДВИЖЕНИЯ
Vx V0 at;axt 2
S x V0 xt
;
2
ax 2
V0 x
Sx t 2
t ;
2
ax
ax 2
V0 x V02x V02x
Sx t 2
t 2 2 ;
2
ax
ax ax
ax 2
V0 x V02x V02x
Sx t 2
t 2
;
2
ax
a x 2a x
2
ax V0 x V02x
Sx t
.
2
a x 2a x
Vx V0 at;
31. 9. СВОБОДНОЕ ПАДЕНИЕ
V V0 at ;Vx V0 cos ;
Vy V0 sin gt ;
x x0 V0 cos t;
gt 2
y y0 V0 sin t
.
2
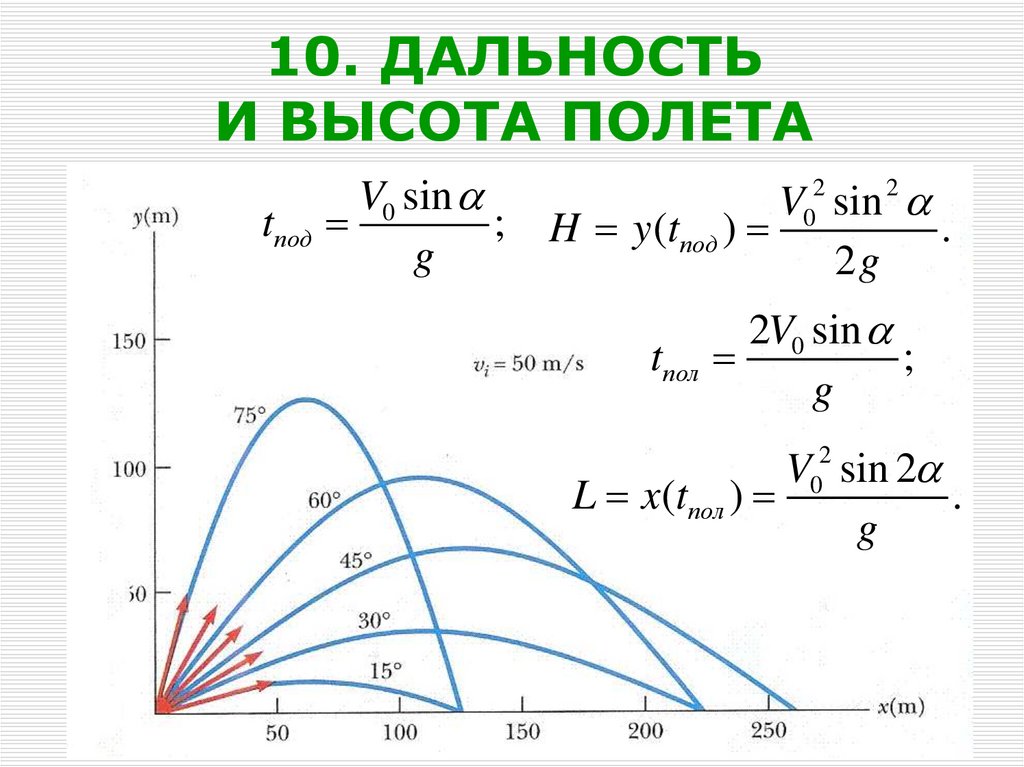
32. 10. ДАЛЬНОСТЬ И ВЫСОТА ПОЛЕТА
tподV0 sin
;
g
V02 sin 2
H y (tпод )
.
2g
tпол
2V0 sin
;
g
V02 sin 2
L x(tпол )
.
g
33. §4. КИНЕМАТИКА ДВИЖЕНИЯ ПО ОКРУЖНОСТИ
34. 1. ПЕРИОД И ЧАСТОТА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
dt2 R
T
; T
;
dN
V
dN
1
;
dt
T
T 1c; 1c
1
1Гц;
35. 2. РАВНОМЕРНОЕ ВРАЩЕНИЕ
2;
t
T
2 ;
рад
1 ;
с
36. 3. РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЕ
d;
dt
d z
z z
;
dt
z ;
рад
1 2 .
с
37. 4. УГЛОВАЯ И ЛИНЕЙНАЯ СКОРОСТИ
dl dV
;
dt
dt
r sin V r sin ;
r r sin ;
V r
V r ;
38. 5. УГЛОВОЕ И ЛИНЕЙНОЕ УСКОРЕНИЯ
a V R R;2
n
dV d
a
z R
dt dt
d z
a R
R z ;
dt
d
d
r
d
V
d
a
r a r r V ;
dt dt
dt dt
2
a r ;
an V r r r ;































 physics
physics








