Similar presentations:
Кинематика. Траектория точки
1. КИНЕМАТИКА –
раздел механики,изучающий
геометрические свойства
движения тел
без учета их масс
и действующих на них сил.
2. ТРАЕКТОРИЯ ТОЧКИ –
геометрическоеместо
последовательных
положений
движущейся точки
в рассматриваемой
системе отсчета
По виду траектории
все движения точки
делятся
на прямолинейные
и криволинейные
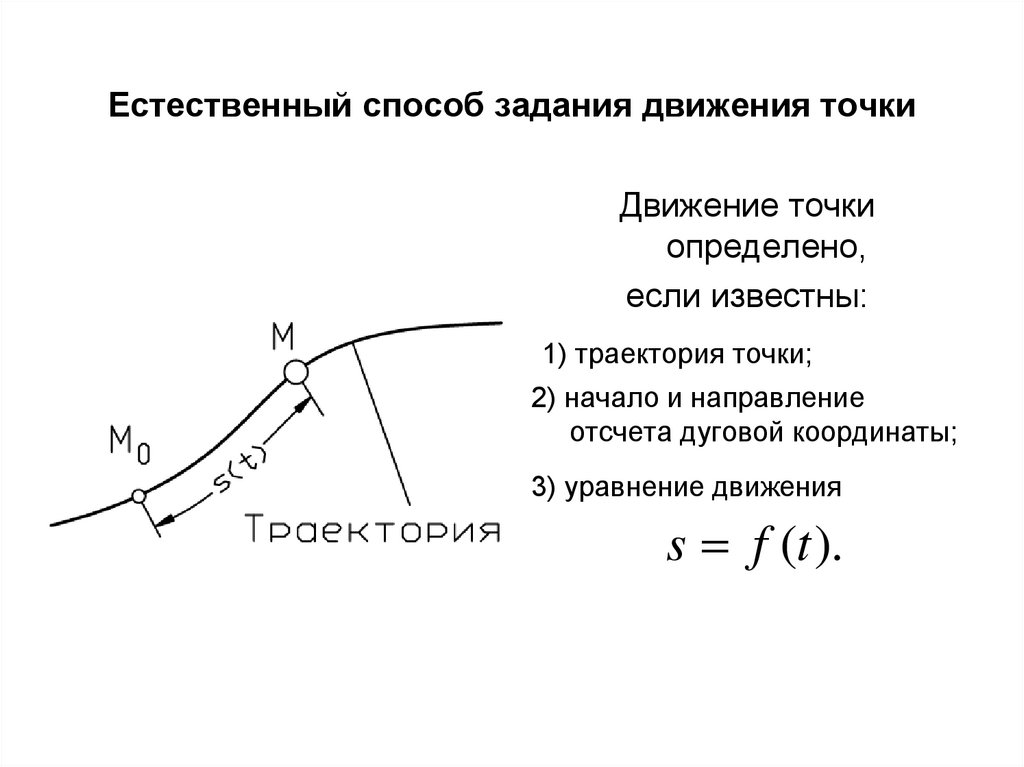
3. Естественный способ задания движения точки
Движение точкиопределено,
если известны:
1) траектория точки;
2) начало и направление
отсчета дуговой координаты;
3) уравнение движения
s f (t ).
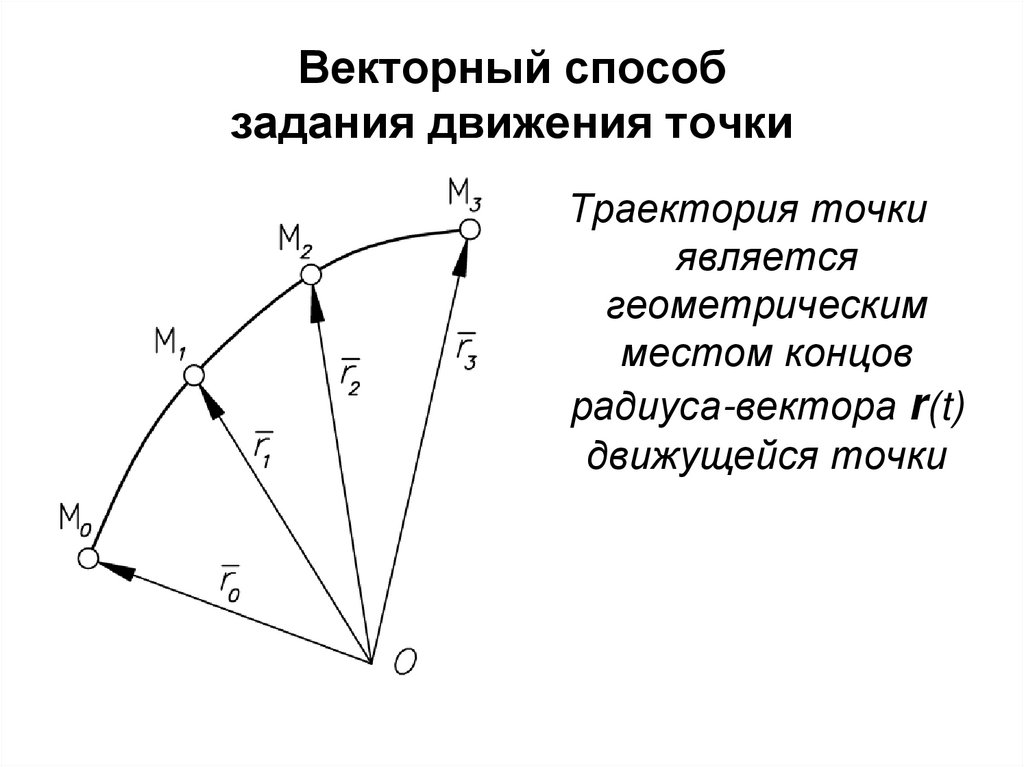
4. Векторный способ задания движения точки
Траектория точкиявляется
геометрическим
местом концов
радиуса-вектора r(t)
движущейся точки
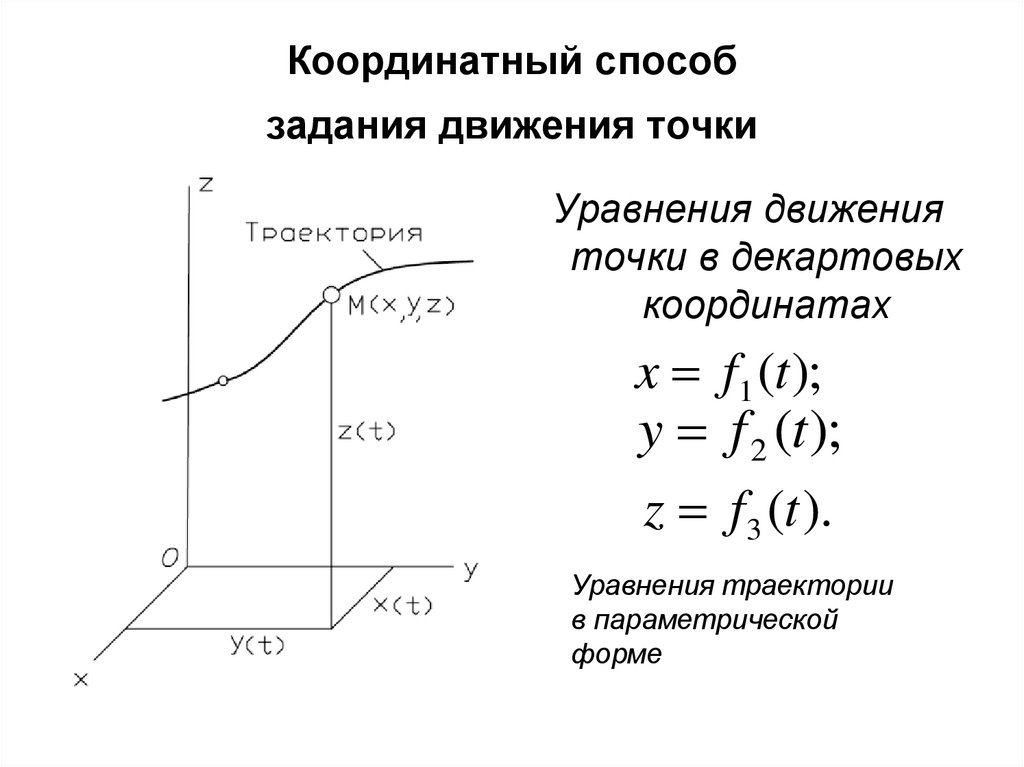
5. Координатный способ задания движения точки
Уравнения движенияточки в декартовых
координатах
x f1 (t );
y f 2 (t );
z f3 (t ).
Уравнения траектории
в параметрической
форме
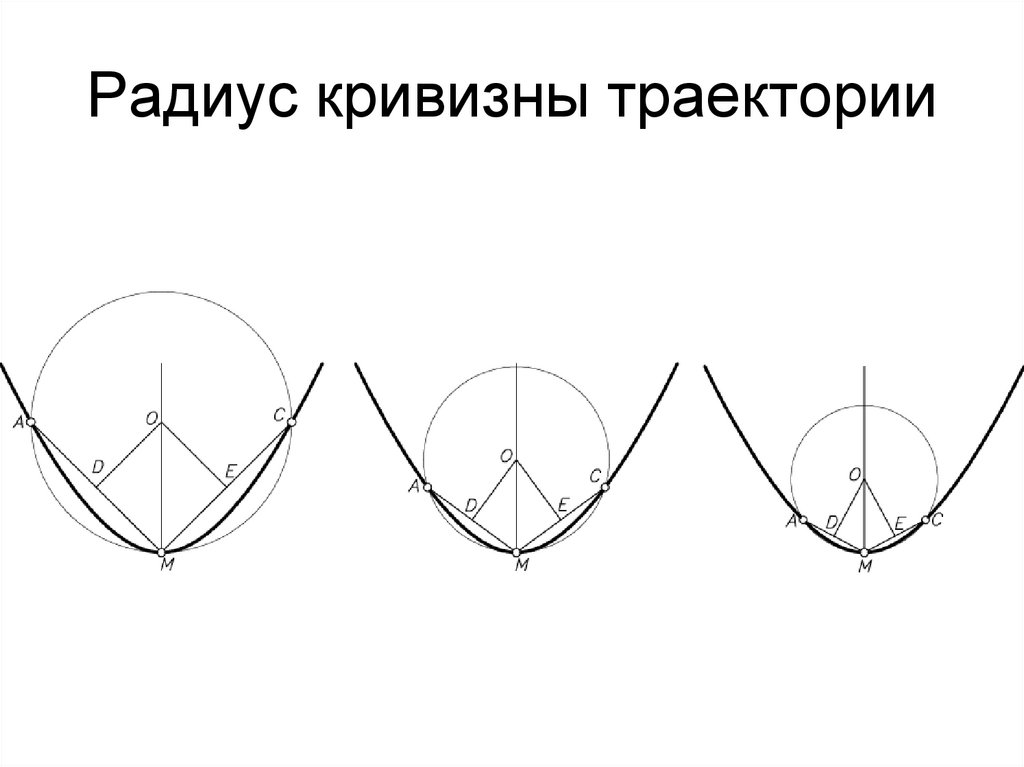
6. Радиус кривизны траектории
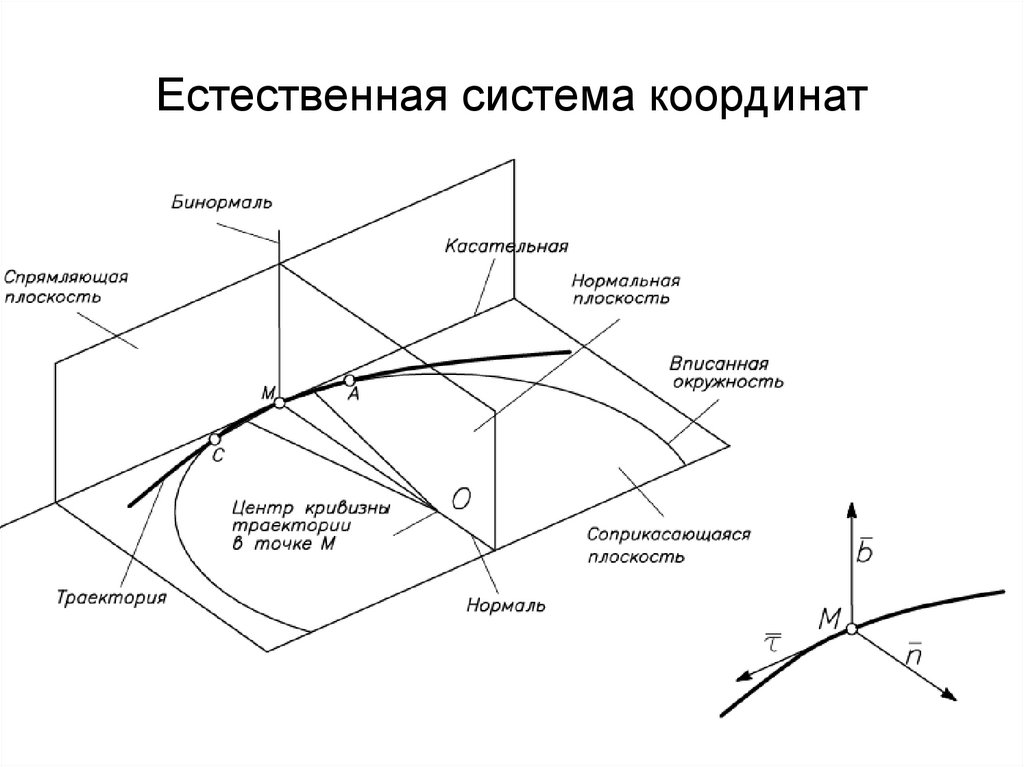
7. Естественная система координат
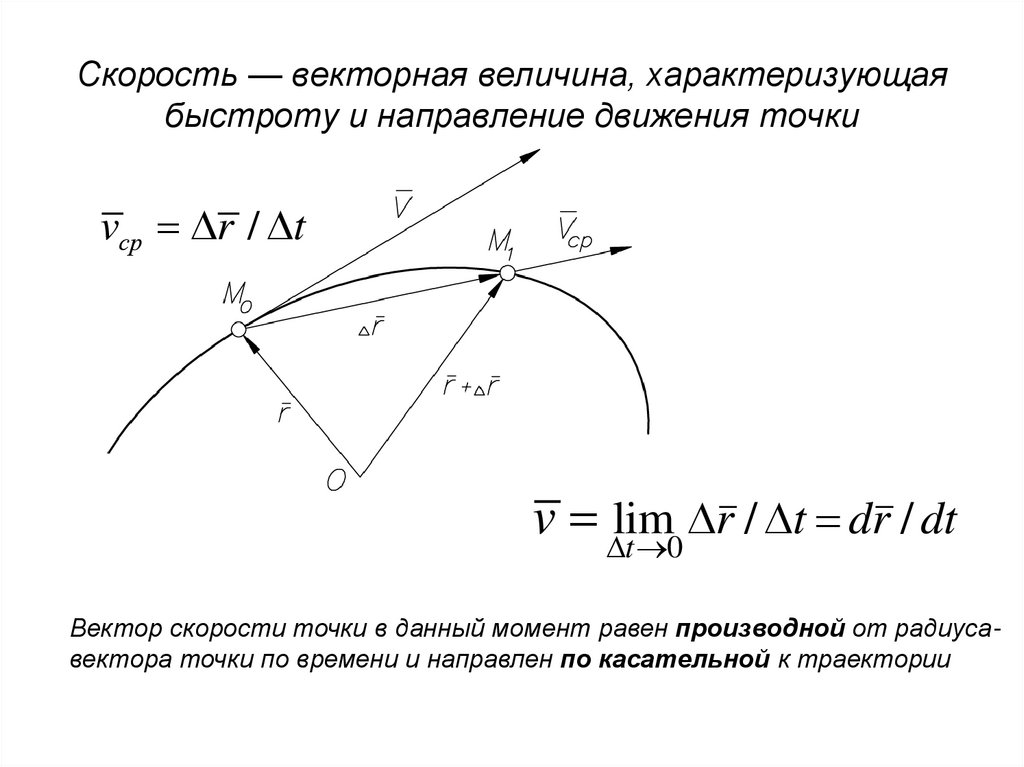
8. Скорость — векторная величина, характеризующая быстроту и направление движения точки
vср r / tv lim
r / t dr / dt
t 0
Вектор скорости точки в данный момент равен производной от радиусавектора точки по времени и направлен по касательной к траектории
9. Определение скорости точки при задании ее движения естественным способом. Проекции скорости на касательную к траектории
v dr (s,t )/ dt (dr / ds)(ds / dt );dr / ds lim r / s dr / dt;
s 0
r
1;
s
lim
s 0
dr / ds;
v ds / dt
Модуль скорости равен
абсолютному значению производной
от дуговой координаты точки по времени
10. Определение скорости точки при задании ее движения координатным cпособом. Проекции скорости точки на неподвижные оси декартовых
координатПусть заданы уравнения движения точки
x f1 (t );
y f 2 (t );
z f 3 (t )
r ix jy kz
v dr / dt i dx / dt j dy / dt k dz / dt
v i vx j vy k vz
11. Проекции скорости точки на неподвижные оси декартовых координат равны первым производным от соответствующих координат точки по
времениvx dx / dt ;
v y dy / dt ;
vz dz / dt.
v v v v
2
x
2
y
2
z
12. УСКОРЕНИЕ ТОЧКИ
При неравномерном криволинейномдвижении точки изменяются модуль и
направление ее скорости.
Ускорение точки характеризует
быстроту изменения модуля и
направления скорости точки.
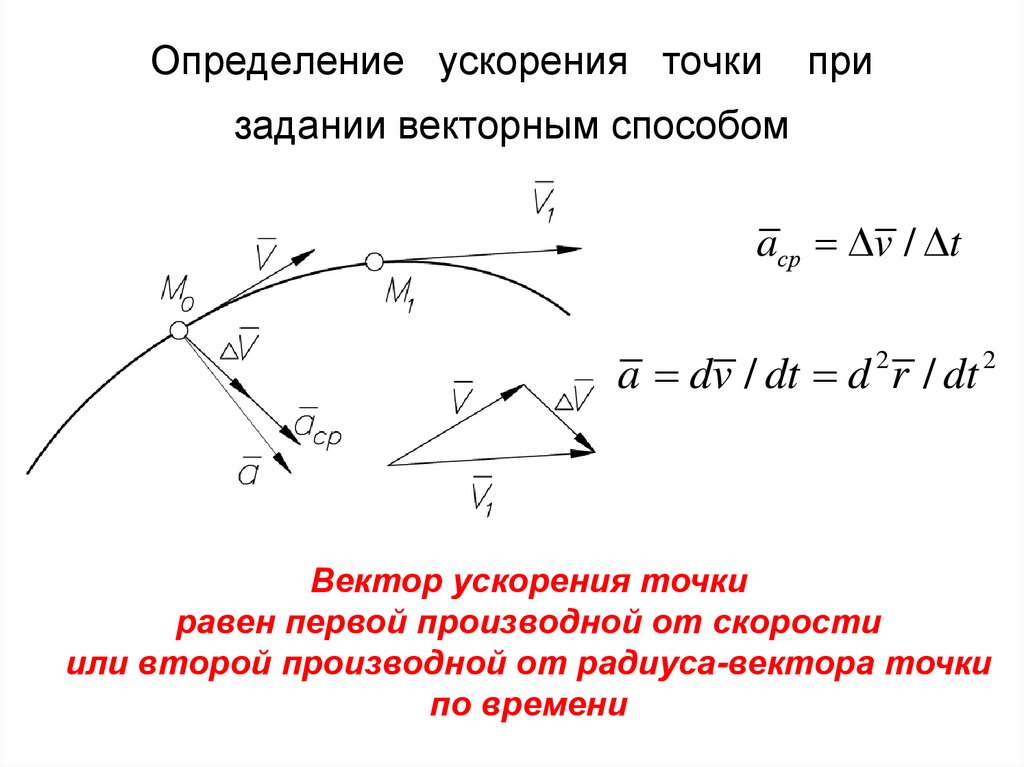
13. Определение ускорения точки при задании векторным способом
aср v / ta dv / dt d r / dt
2
2
Вектор ускорения точки
равен первой производной от скорости
или второй производной от радиуса-вектора точки
по времени
14. Определение ускорения точки при задании ее движения координатным способом
r i x jy kz(1)
2
2
2
2
2
2
2
a d r / dt i d x / dt j d y / dt k d z / dt 2
a i ax j a y k az
(3)
ax d x / dt ; ay d y / dt ; az d z / dt
2
2
2
a x dv x / dt ; a y dv y / dt ;
2
2
a z dv z / dt
a ax2 a y2 az2
2
(4)
(5)
(2)
15. Определение ускорения точки при задании ее движения естественным способом. Касательное и нормальное ускорения точки
v ds / dt(1)
dv d ds
d 2s
a
2
dt dt dt
dt
2
d ds ds
d s
2
ds dt dt
dt
d 2
d 2s
v 2
ds
dt
(2)
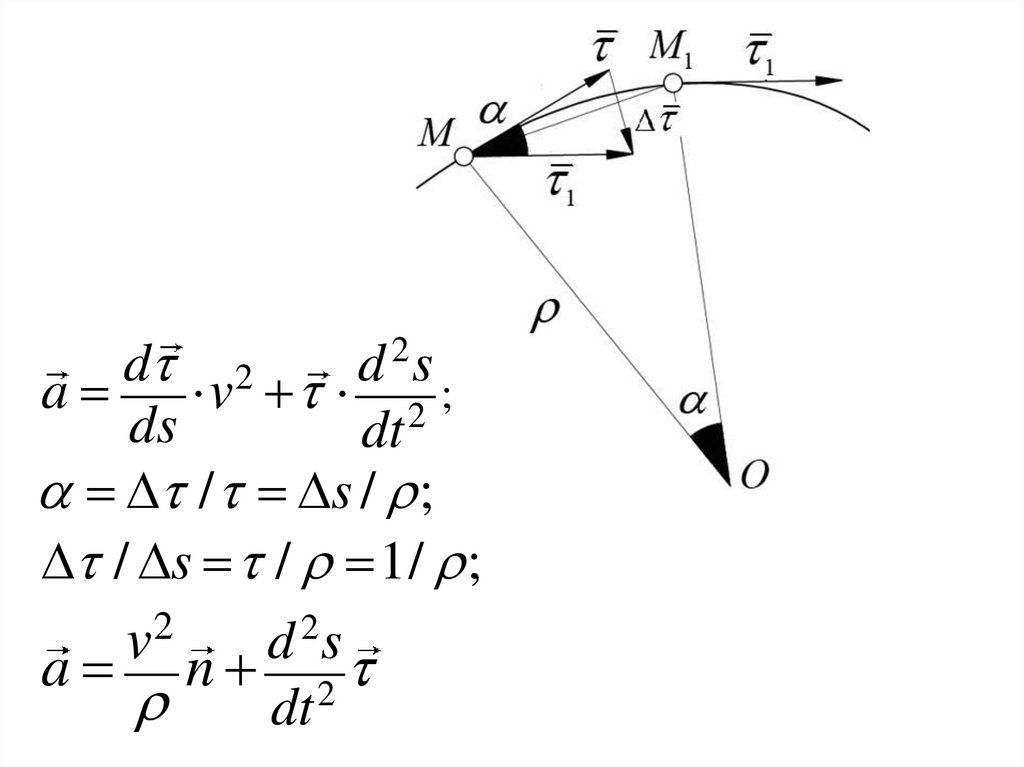
16.
d 2d 2s
a
v 2 ;
ds
dt
/ s / ;
/ s / 1/ ;
2
v
d 2s
a n 2
dt
17.
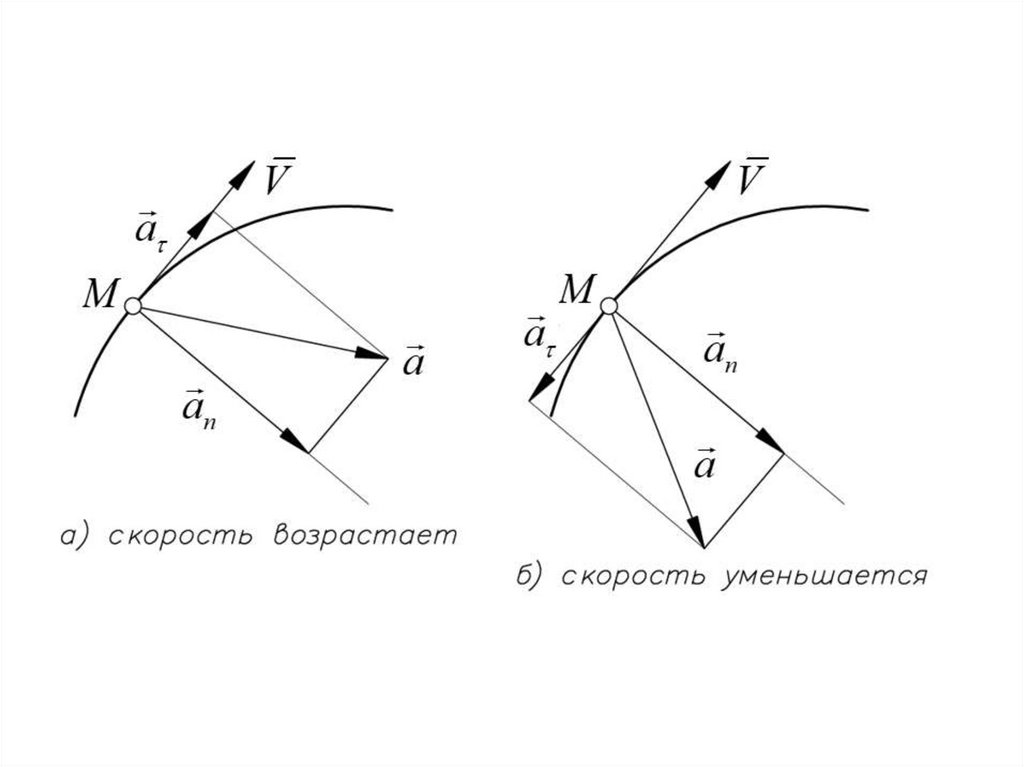
Ускорение точки равногеометрической сумме двух векторов, один из которых направлен
по главной нормали и называется
нормальным ускорением,
а другой направлен по касательной и называется
касательным ускорением точки
a an a
где нормальное ускорение точки
а касательное ускорение
an n v / ,
2
a d s / dt
2
2
Нормальное ускорение существует лишь при криволинейном
движении точки и характеризует изменение направления скорости.
Касательное ускорение точки существует лишь при неравномерном
движении точки и характеризует изменение модуля скорости
18.
19. Определение касательного и нормального ускорения точки, движение которой задано координатным способом
v vx2 v y2 vz2 ;dv
d
a
v x2 v y2 v z2
dt
dt
или
a
a ax2 a y2 az2
dv y
dv x
dv z
vx
vy
vz
dt
dt
dt
v x2 v y2 v z2
vx a x v y a y v z a z
v
.
Радиус кривизны траектории находим по формуле
an a a
2
v / an
2
2
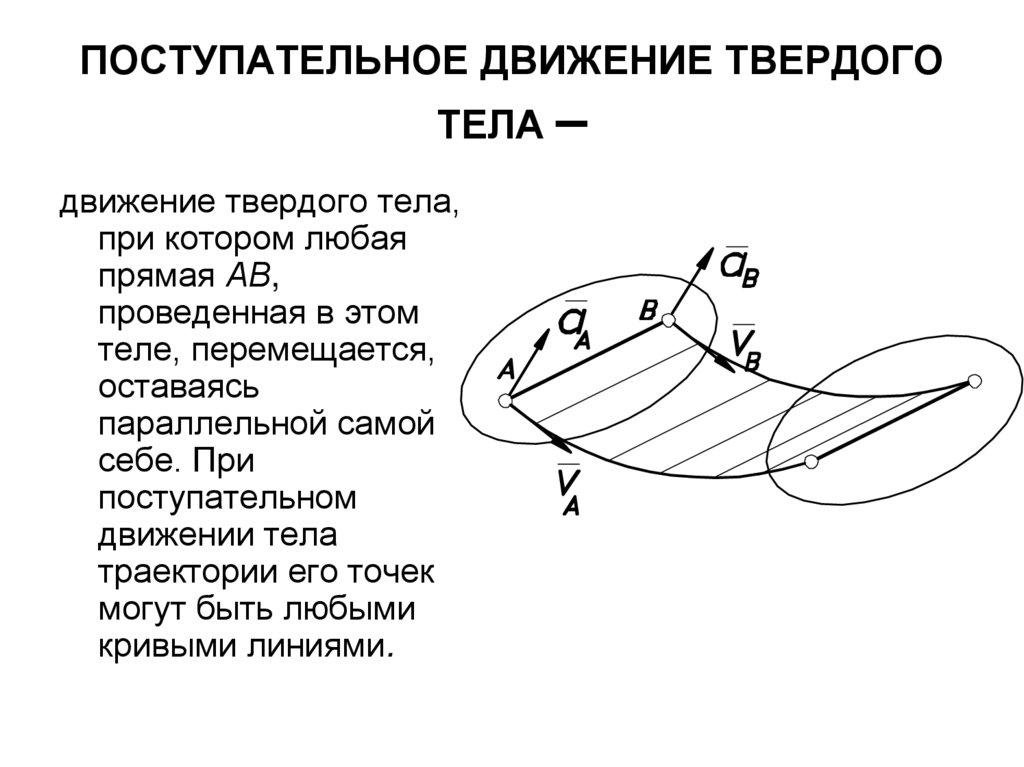
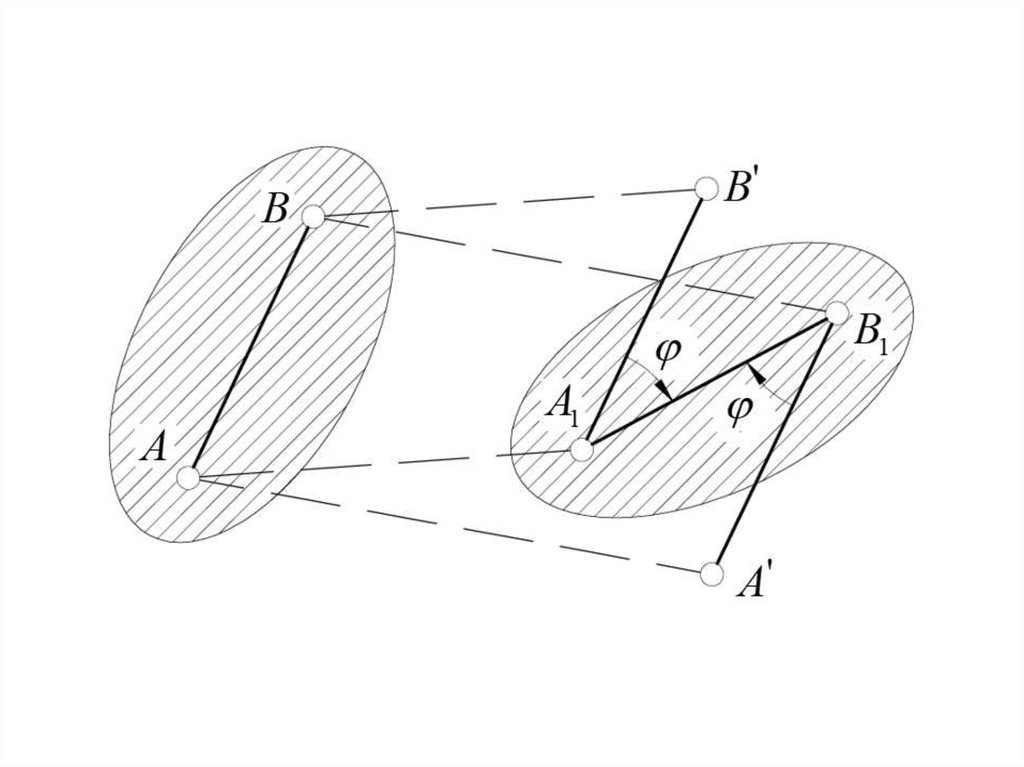
20. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА –
движение твердого тела,при котором любая
прямая АВ,
проведенная в этом
теле, перемещается,
оставаясь
параллельной самой
себе. При
поступательном
движении тела
траектории его точек
могут быть любыми
кривыми линиями.
21.
При поступательном движениивсе точки тела описывают
одинаковые (при наложении
совпадающие) траектории
и имеют в каждый момент времени
одинаковые
по модулю и направлению
скорости
и ускорения
22.
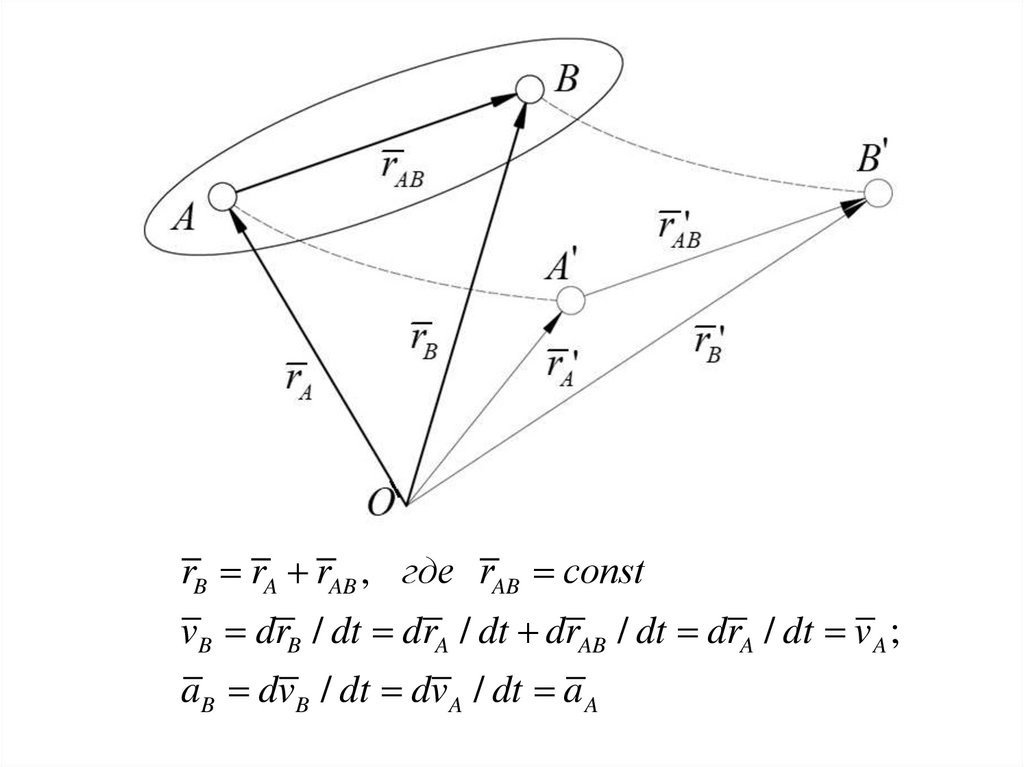
rB rA rAB , где rAB constvB drB / dt drA / dt drAB / dt drA / dt v A ;
aB dvB / dt dv A / dt a A
23. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА –
движение твердого тела, при которомкакие-нибудь две точки,
принадлежащие телу (или неизменно с
ним связанные), остаются во все время
движения неподвижными
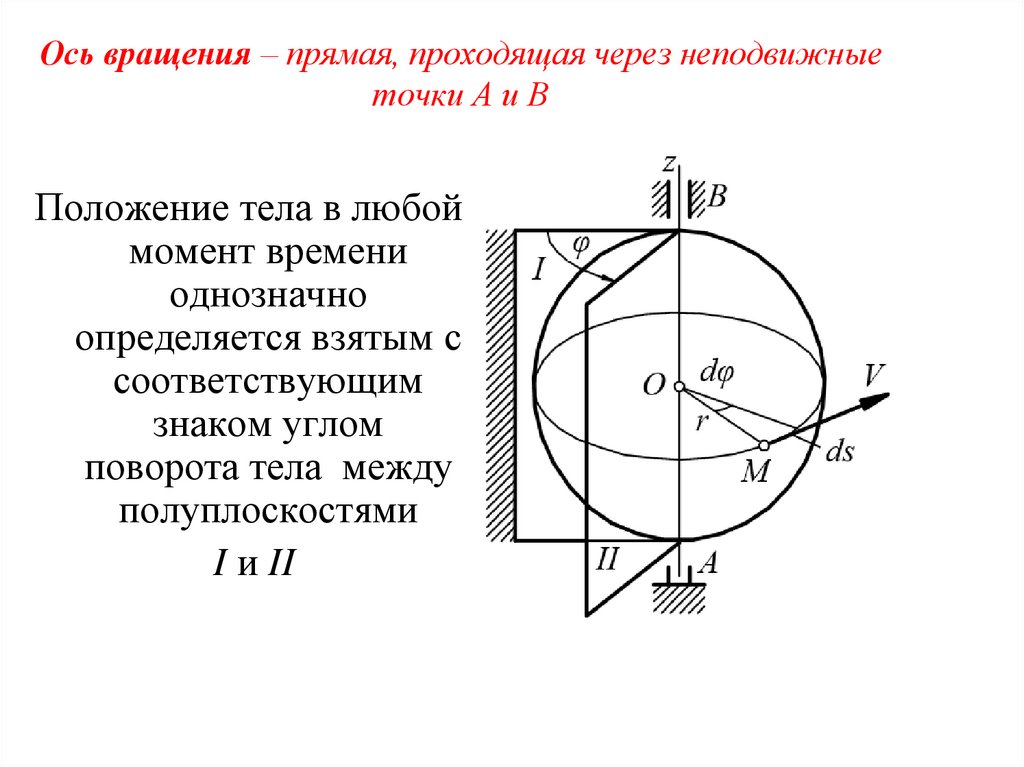
24. Ось вращения – прямая, проходящая через неподвижные точки А и В
Положение тела в любоймомент времени
однозначно
определяется взятым с
соответствующим
знаком углом
поворота тела между
полуплоскостями
I и II
25. Измеряется угол в радианах
Угловая скорость - быстрота изменения углаповорота:
d
lim
t 0
t
dt
[сек 1 ]
Угловое ускорение - быстрота изменения угловой скорости :
d d 2
lim
2 [сек 2 ]
t 0 t
dt dt
26.
v ds r d r ;Линейная скорость точки
dt
v2
an 2 r;
r
Нормальное ускорение
Тангенциальное ускорение
a
dv
d
a r
r
dt
dt
2
a an
2
dt
r
2
4
27. Вращение равномерное – вращение тела с постоянной угловой скоростью.
dconst
dt
d dt;
t
0
0
d
dt
;
откуда
t 0
28. Вращение равнопеременное – вращение тела с постоянным угловым ускорением
dconst;
dt
d dt;
t
d
dt
;
0
0
d / dt t 0 ; d ( t 0 )dt;
t
t
d 0 t dt 0 0 dt;
0
0 0t
2
t
2
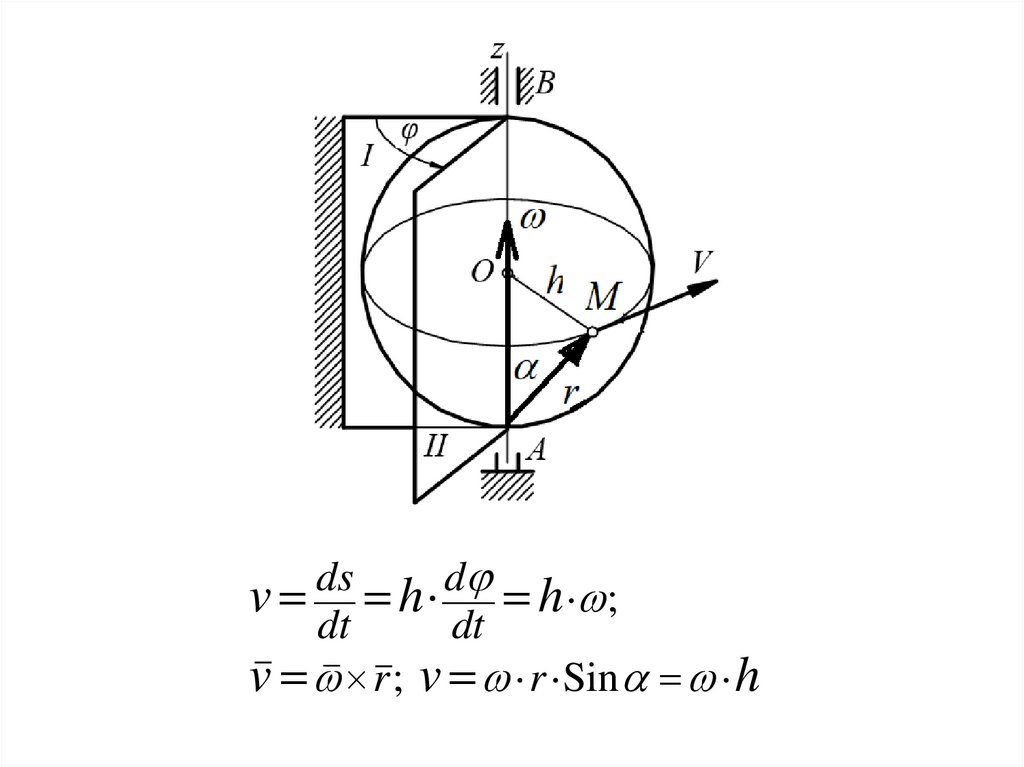
29.
dsd
v h h ;
dt
dt
v r ; v r Sin h
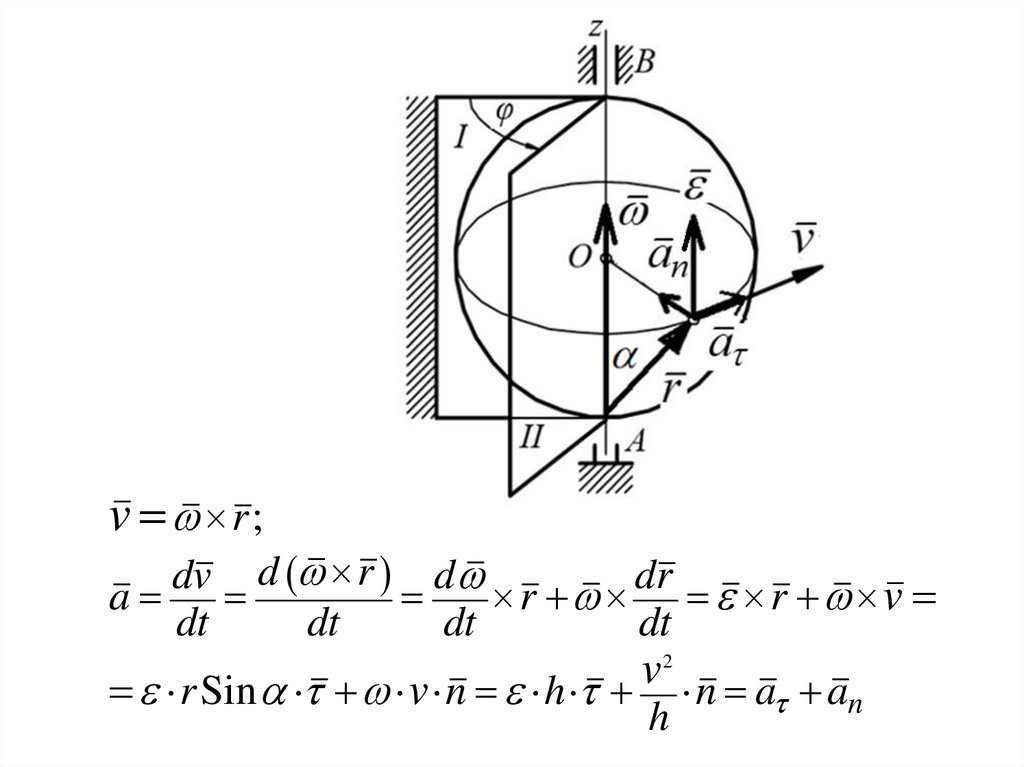
30.
v r;dv d r d
dr
a
r r v
dt
dt
dt
dt
2
v
r Sin v n h n a an
h
31.
Плоскопараллельное (плоское)движение твердого тела –
движение, при котором все его точки
перемещаются параллельно некоторой
неподвижной плоскости
32.
33.
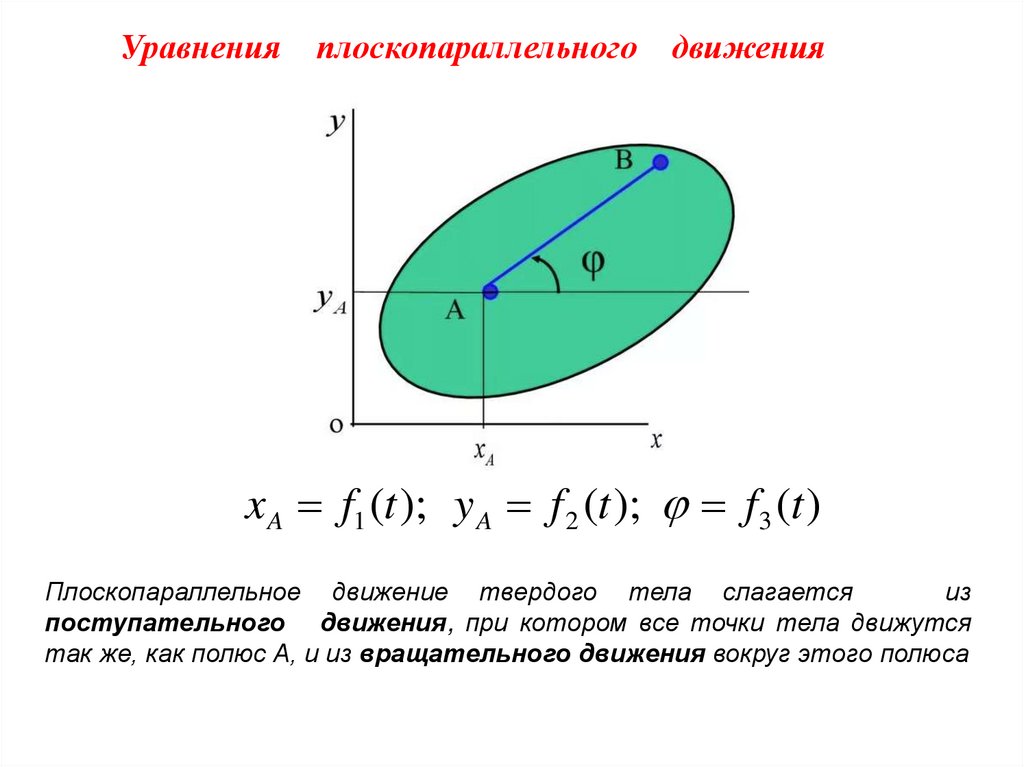
Уравненияплоскопараллельного
движения
xA f1 (t ); y A f 2 (t ); f 3 (t )
Плоскопараллельное движение твердого тела слагается
из
поступательного движения, при котором все точки тела движутся
так же, как полюс А, и из вращательного движения вокруг этого полюса
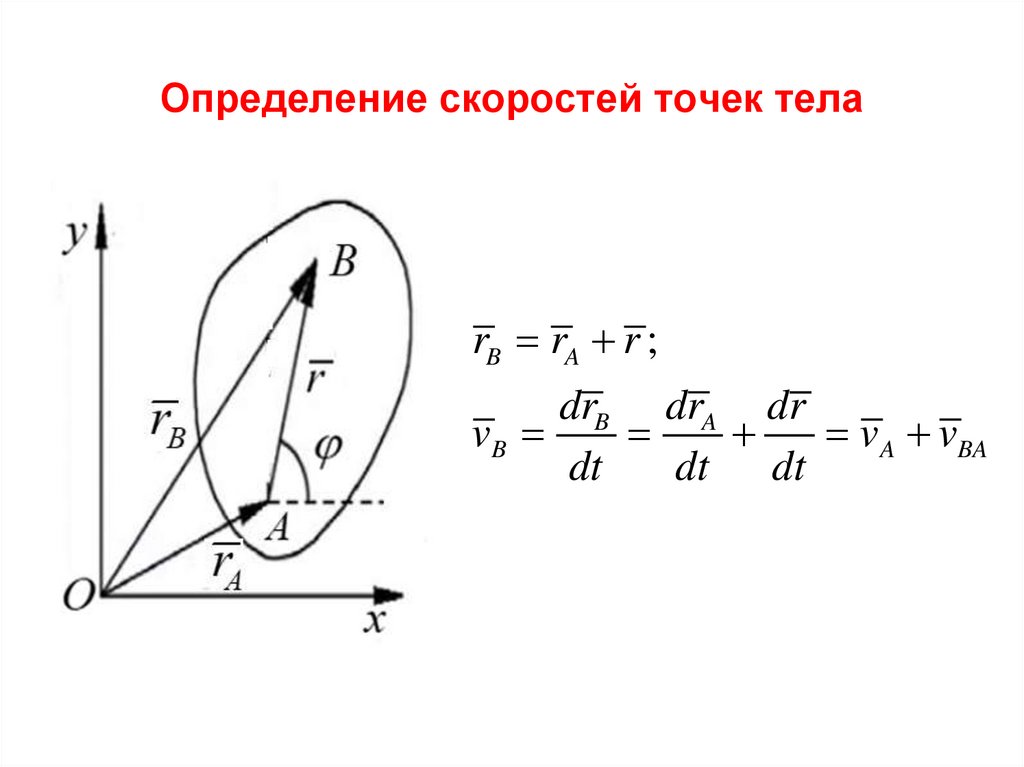
34. Определение скоростей точек тела
rB rA r ;drB drA dr
vB
v A vBA
dt
dt dt
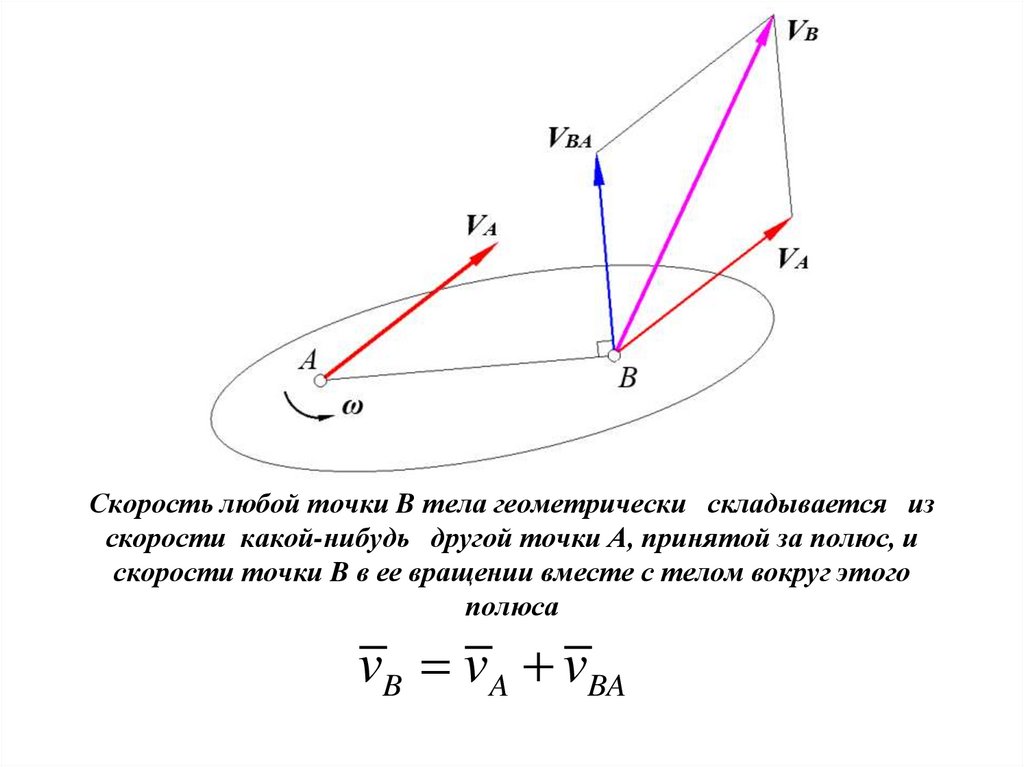
35. Скорость любой точки B тела геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости
точки B в ее вращении вместе с телом вокруг этогополюса
vB vA vBA
36. Теорема о проекциях скоростей двух точек тела
vB vA vBAvBA перпендикулярен
ПрABvB ПрABvA
Так как
то
AB,
37.
Мгновенным центромскоростей
называется точка P сечения S
тела,
скорость которой в данный
момент времени равна нулю
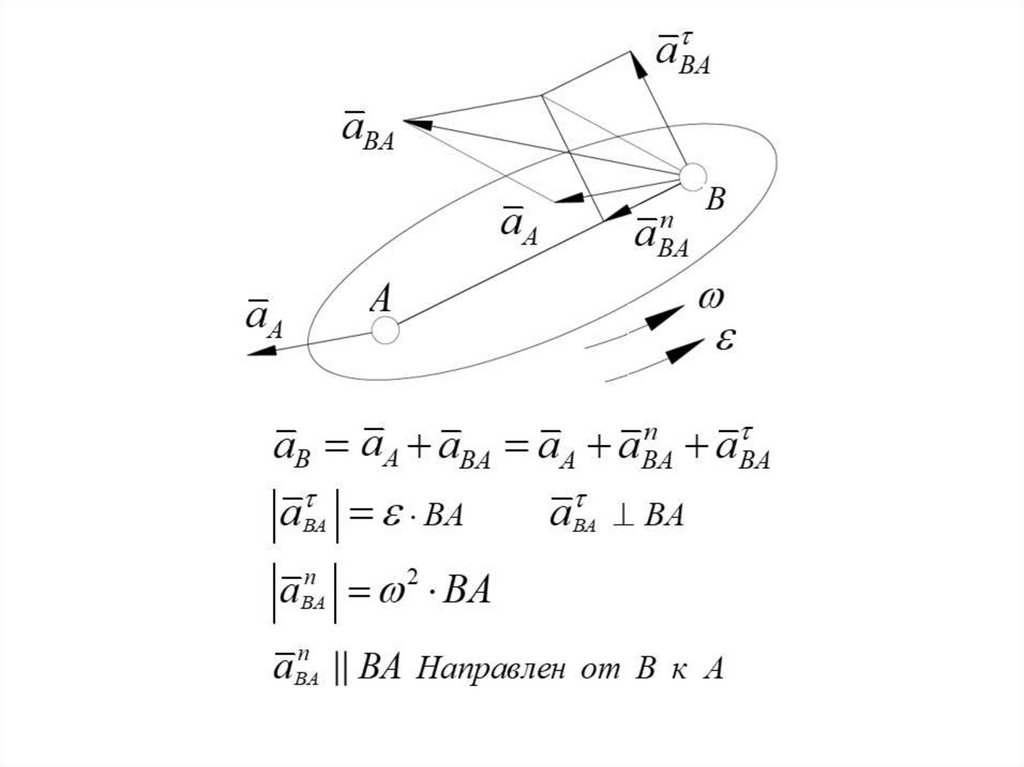
38. Определение ускорений точек тела
vB vA vBA ;aB
dvB
dt
dvA
dt
dvBA
dt
39.
40.
Сферическим называют движениетела относительно
некоторой неподвижной точки
41.
Сложное движение –движение материальной точки
относительно какой-либо системы
отсчёта,
а та, в свою очередь,
движется относительно другой системы
отсчёта (СО)
42.
Одну из СО принимают за базовую(«абсолютную», «лабораторную», «неподвижную»,
«СО неподвижного наблюдателя»),
другую называют «подвижной»
(«СО подвижного наблюдателя»,«второй»)
43.
Абсолютное движение движение материальной точки/телав базовой системе отсчёта
44.
Относительное движение движение материальной точки/телаотносительно подвижной системы
отсчёта
45.
Переносное движение движение подвижной системы отсчета ивсех постоянно связанных с нею
точек пространства
относительно базовой системы отсчета
46.
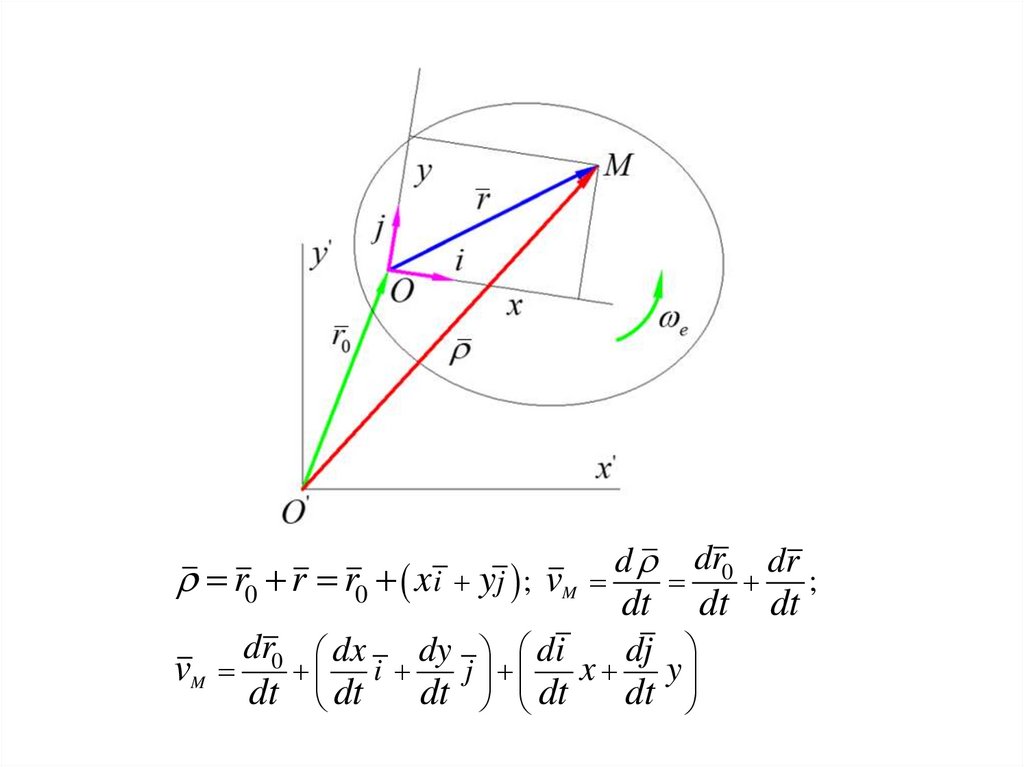
r0 r r0 x i yj ; vMvM
dr0 dx
dy di
dt
dt
i
dt
j
dt
d
dt
dr0 dr
dt
dj
x y
dt
dt
;
47.
didj
x y
dt
dt
vM
e i x e j y e ix jy e r ;
dr0 dx
dy
dt
dt
i
dt
j e r vO vr ve
48.
e i x e j y e ix jy e r ;di
dj
y
x
dt
dt
vM
dr0
aM
dvM
dt
dt
vx i vy j e x i yj ;
d 2 r0 dvx
dt
2
di
dj
v
v
x
y
dt
dt
e
d xi yj
aM
dt
dt
di
dt
dt
j vx
vy
dj d e
dt
dt
v i v j v i v
x
e
y
e
e
x
y
r e
dv y
j v r e e r e vr
i
dt e r e
dt 2 dt
2
dt
i
dv y
dt
j e r e e r 2 e vr ;
d xi yj
j e vr
e vr e e r ;
d 2 r0 dvx
d 2 r0 dvx
dt
i
dv y
dt
;
49.
aM aОтн aПер aКор ;aОтн
dvx
i
dv y
j ax i a y j ;
dt
dt
aПер e r e e r ;
aКор 2 e vr



























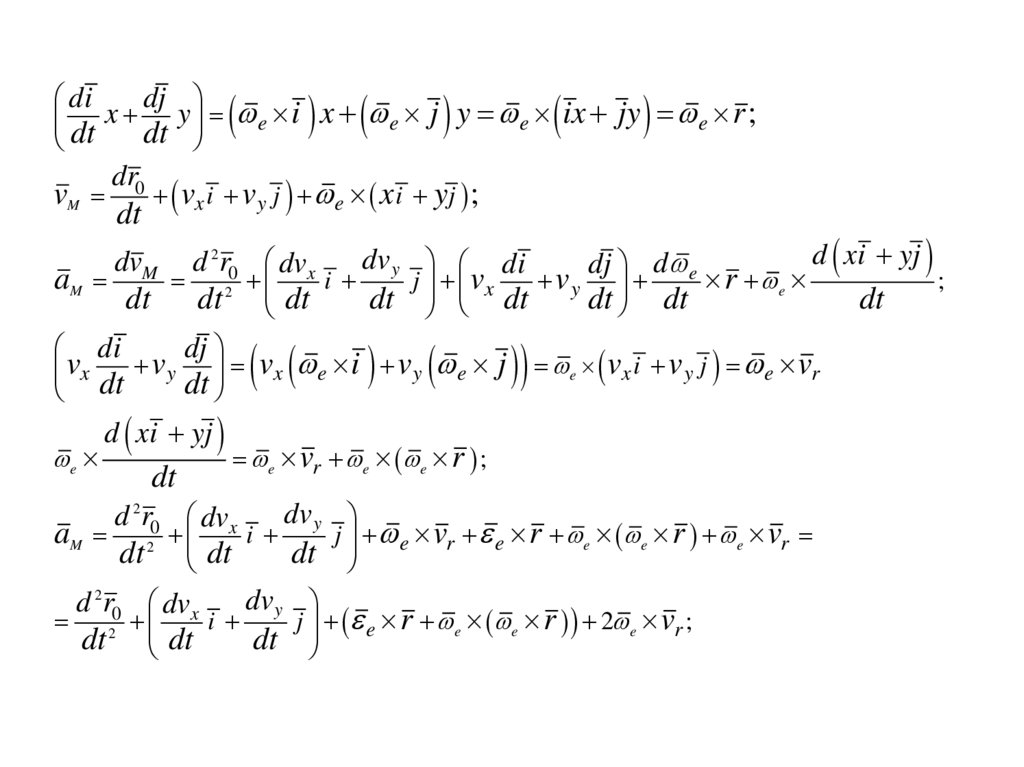
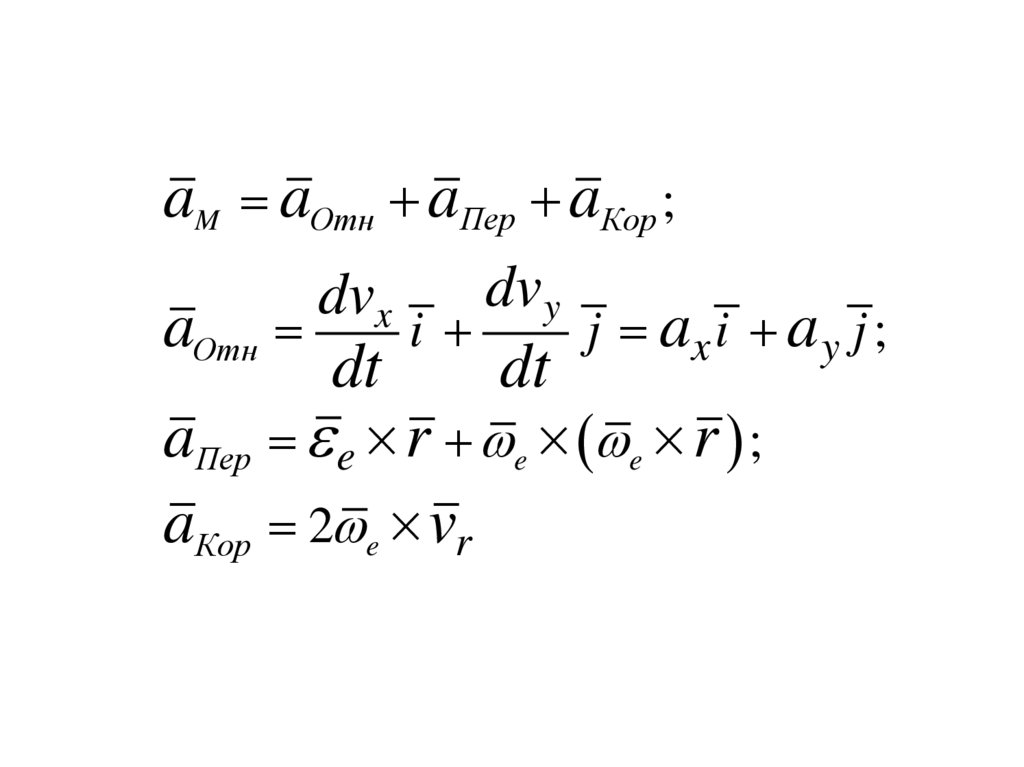
 physics
physics








