Кинематика движения материальной точки

1. Лекция 1. КИНЕМАТИКА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ

• 1. Понятие механики, модели в механике
• 2. Система отсчета, тело отсчета
• 3. Кинематика материальной точки
– 3.1. Траектория, путь, перемещение
– 3.2. Скорость
– 3.3. Проекция вектора скорости на оси координат
– 3.4. Ускорение. Нормальное и тангенциальное
ускорение
• 4. Кинематика вращательного движения твердого тела
– 4.1. Поступательное движение твердого тела
– 4.2. Вращательное движение вокруг неподвижной
оси
– 4.3. Связь между линейными и угловыми величинами
при вращательном движении
Лектор: Мухамедгалиева Майра Айсагалиевна
E-mail: [email protected]
1

2.

1. Понятие механики, разделы в
механике
Механика - часть физики, которая изучает
закономерности механического движения и причины,
вызывающие или изменяющие это движение.
Механическое движение - изменение взаимного
положения тел или их частей в пространстве со
временем.
Механика
Классическая
(механика ГалилеяНьютона)
Изучает законы движения
макроскопических тел,
скорости которых малы
по сравнению со скоростью
света в вакууме с.
v/c <<1
Релятивистская –
Квантовая –
изучает законы движения
макроскопических тел со
скоростями, сравнимыми с с.
Основана на СТО.
Изучает законы движения
микроскопических тел
(отдельных атомов и
элементарных частиц)

3.

Предметом классической механики является механическое
движение взаимодействующих между собой макротел при
скоростях, много меньше скорости света и в условиях, когда
переходом механической энергии в другие ее формы можно
пренебречь.
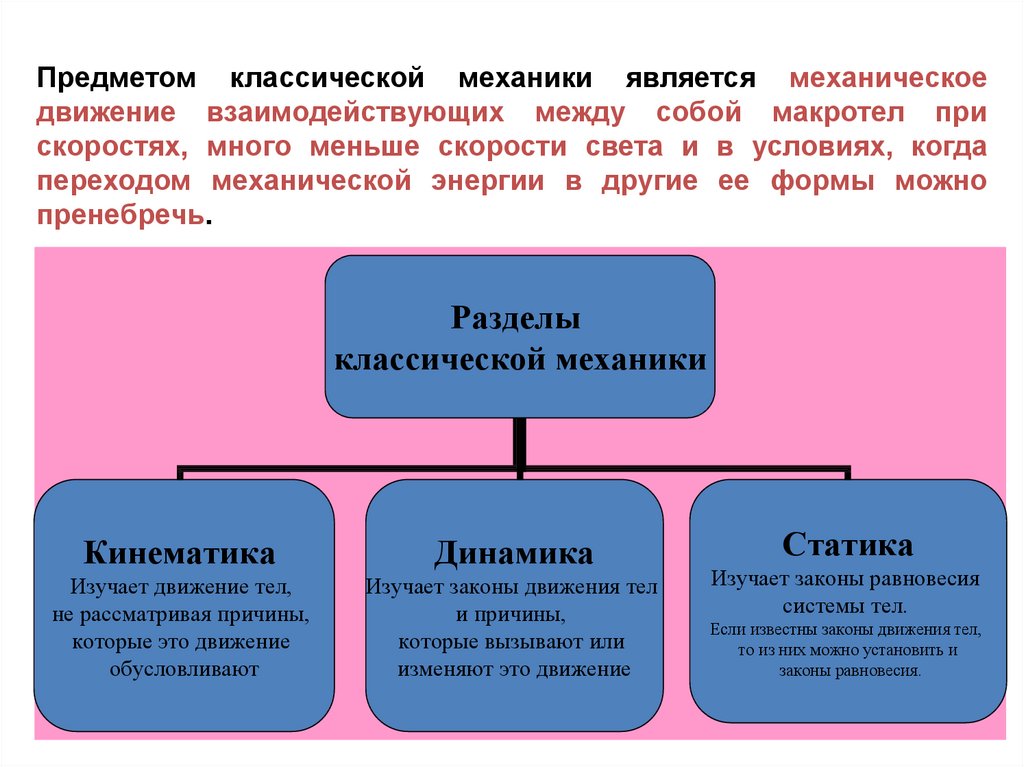
Разделы
классической механики
Кинематика
Динамика
Изучает движение тел,
не рассматривая причины,
которые это движение
обусловливают
Изучает законы движения тел
и причины,
которые вызывают или
изменяют это движение
Статика
Изучает законы равновесия
системы тел.
Если известны законы движения тел,
то из них можно установить и
законы равновесия.

4. Модели в механике

• МАТЕРИАЛЬНАЯ
ТОЧКА
- тело, размерами и формой
которого можно пренебречь в данной задаче.
• АБСОЛЮТНО ТВЕРДОЕ ТЕЛО – тело, деформацией которого
можно пренебречь и считать, что расстояние между любыми
двумя его точками остается неизменным.
• АБСОЛЮТНО УПРУГОЕ ТЕЛО - тело, деформация которого
подчиняется закону Гука, а после прекращения действия
внешних сил оно полностью
восстанавливает
свои
первоначальные размеры и форму.

5. 2.2. Система отсчета, тело отсчета

Всякое движение относительно, поэтому для
описания
движения
необходимо
условиться,
относительно какого другого тела будет отсчитываться
перемещение данного тела. Выбранное для этой цели
тело называют телом отсчета.
Система отсчета – совокупность системы координат и
часов, связанных с телом по отношению к которому
изучается движение.
Движения тела, как и материи, вообще не может
быть
вне
времени
и
пространства.
Материя,
пространство и время неразрывно связаны между
собой (нет пространства без материи и времени и
наоборот).
5

6.

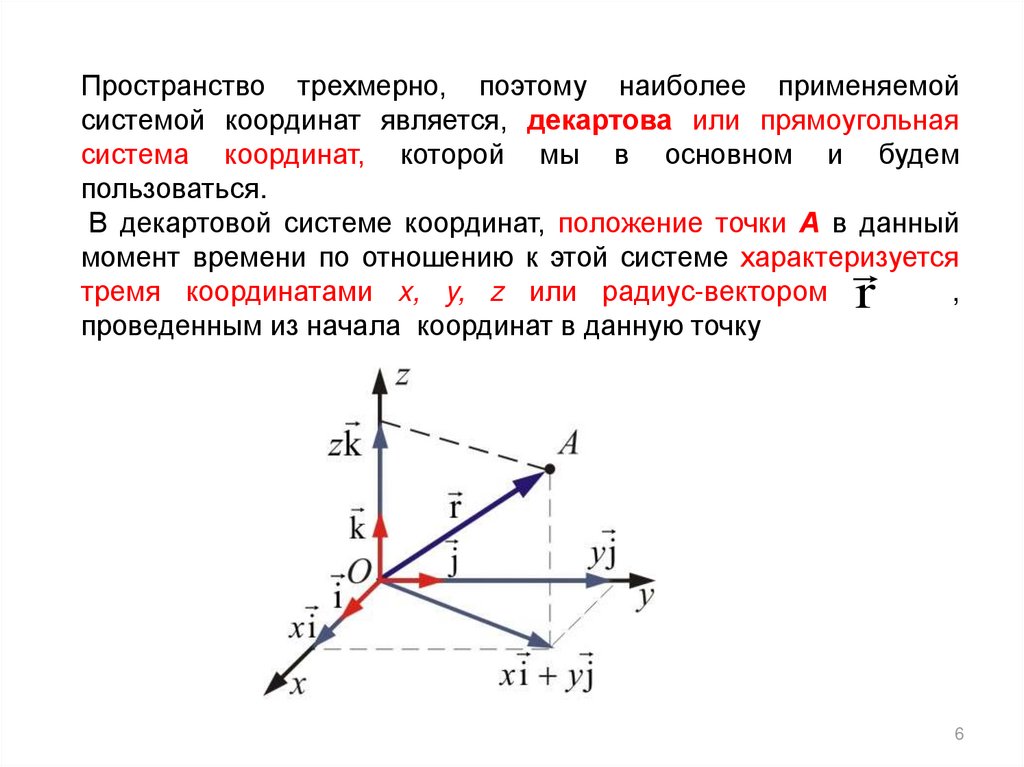
Пространство трехмерно, поэтому наиболее применяемой
системой координат является, декартова или прямоугольная
система координат, которой мы в основном и будем
пользоваться.
В декартовой системе координат, положение точки А в данный
момент времени по отношению к этой системе характеризуется
тремя координатами x, y, z или радиус-вектором
,
проведенным из начала координат в данную точку
r
6

7.

Кинематические уравнения движения
материальной точки:
x x(t ),
y y (t ),
z z (t ).
Эти уравнения эквивалентны векторному уравнению
r x i y j zk
где х, у, z – проекции
r r (t )
радиус-вектора r
на оси координат, а i, j, k – единичные
векторы
(орты),
направленные
по
соответствующим осям.
77

8.

Число
независимых
координат,
полностью определяющих положение точки
в
пространстве,
называется
числом
степеней свободы i
Если материальная точка движется в
пространстве, то она имеет три степени
свободы i=3 (координаты х, у, z). Если она
движется на плоскости – две степени
свободы i=2. Если вдоль линии – одна
степень свободы i=1.
8

9. 2.3. Кинематика материальной точки

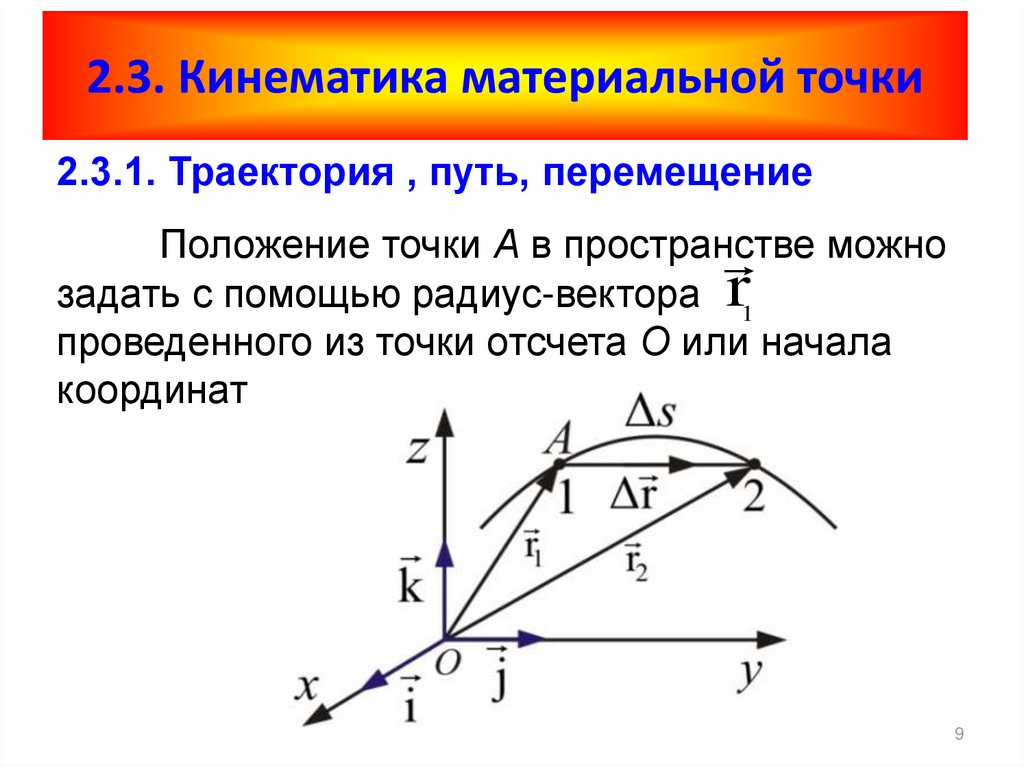
2.3.1. Траектория , путь, перемещение
Положение точки А в пространстве
можно
задать с помощью радиус-вектора r1
проведенного из точки отсчета О или начала
координат
9

10.

r
При движении точки А из точки 1 в точку 2 её радиус-вектор
изменяется и по величине, и по направлению, т.е. зависит
от времени t.
Линия, описываемая движущейся материальной точкой
относительно выбранной системы отсчёта, называется
траекторией её движения.
Длина траектории есть путь Δs. Если точка движется
по прямой, то приращение r равно пути s.
r S

11.

Пусть
за
время
t
точка
переместилась из точки 1 в точку 2.
r
Вектор перемещения
приращение r1 за время t
есть
r r2 r1 x x0 i y y0 j z z0 k;
Δ r Δx i Δy j Δzk
Модуль вектора:
2
2
2
r x y z
А

12. 2.3.2 Скорость

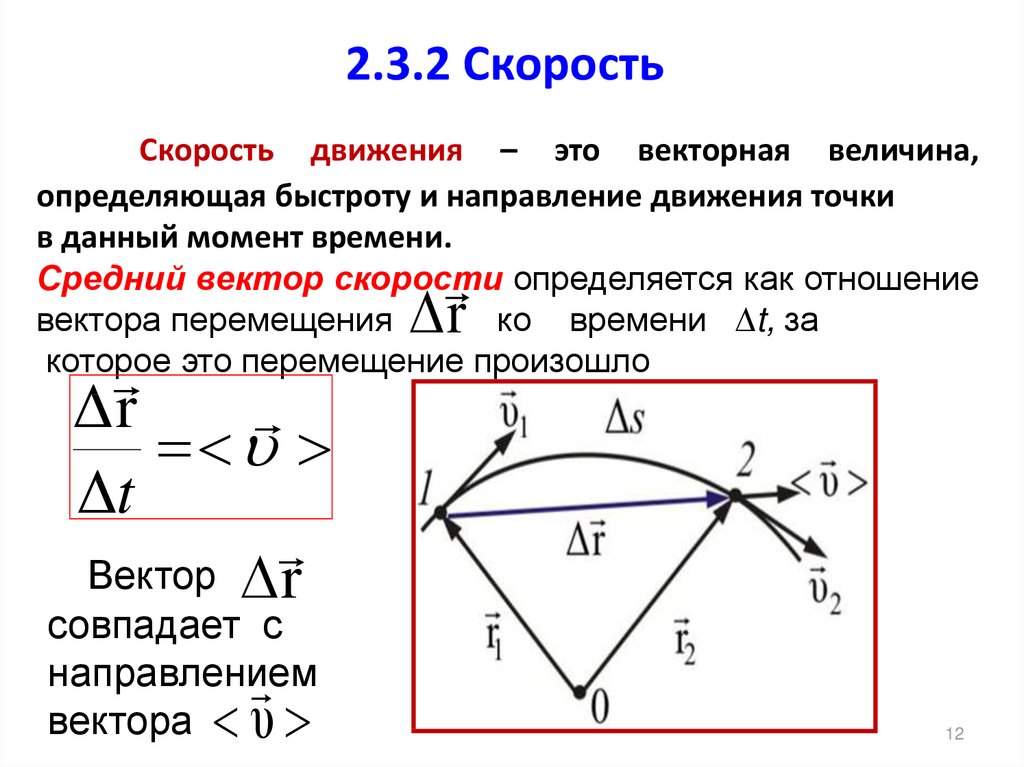
Скорость движения – это векторная величина,
определяющая быстроту и направление движения точки
в данный момент времени.
Средний вектор скорости определяется как отношение
вектора перемещения
ко времени t, за
которое это перемещение произошло
Δr
Δt
Вектор r
совпадает с
направлением
вектора υ
r
12

13.

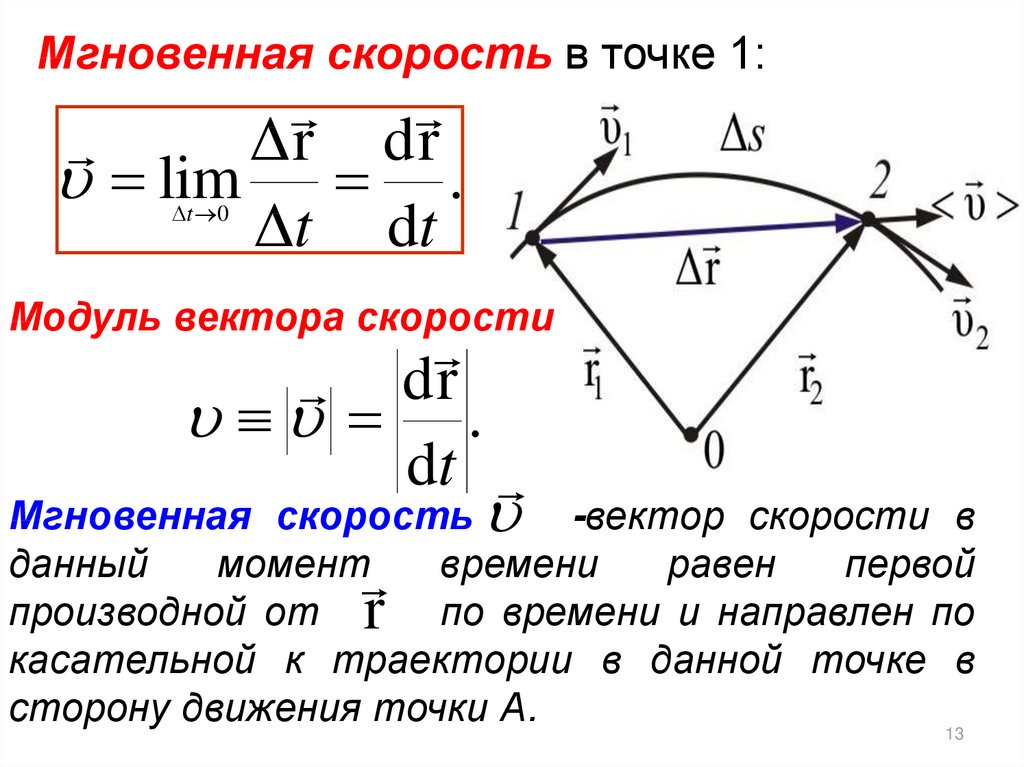
Мгновенная скорость в точке 1:
Δr dr
lim .
Δt dt
Δt 0
Модуль вектора скорости
dr
.
dt
Мгновенная скорость -вектор скорости в
данный
момент времени
равен
первой
производной от r по времени и направлен по
касательной к траектории в данной точке в
сторону движения точки А.
13

14.

При t 0 т.е. на бесконечно малом
участке траектории (перемещение совпадает
с траекторией) r S .
В этом случае мгновенную скорость можно
выразить через скалярную величину – путь:
Δs ds
υ lim
;
Δt 0
Δt dt
ds
или υ .
dt
14

15.

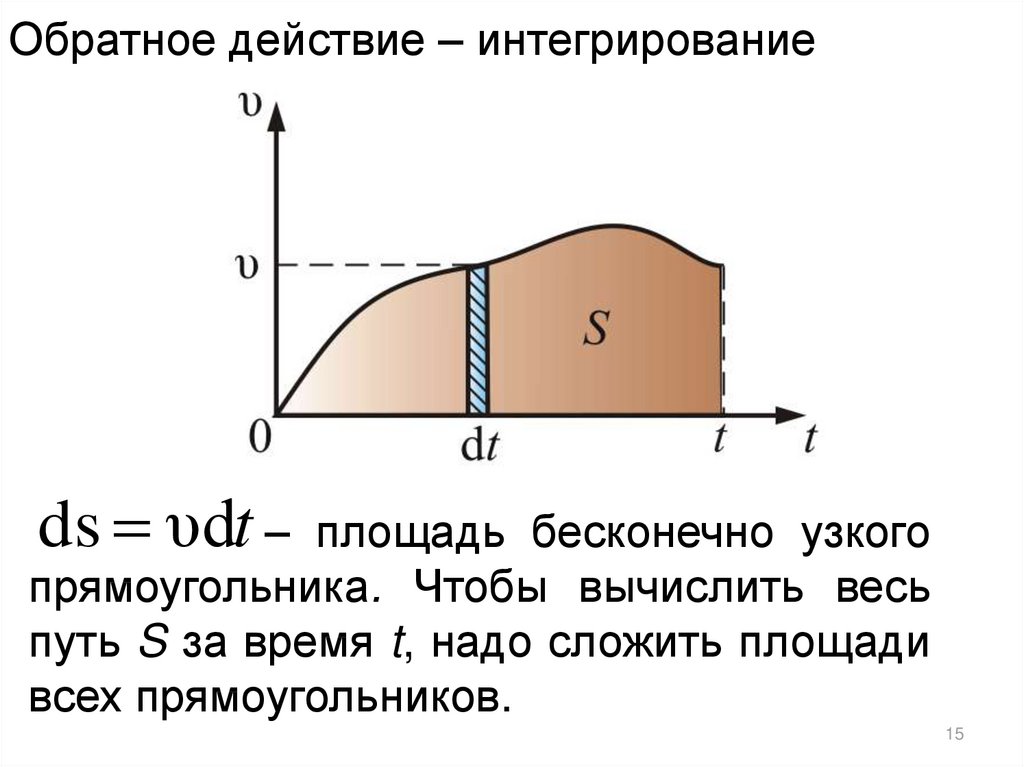
Обратное действие – интегрирование
ds υdt –
площадь бесконечно узкого
прямоугольника. Чтобы вычислить весь
путь S за время t, надо сложить площади
всех прямоугольников.
15

16.

t
S υdt.
0
Геометрический смысл этого интеграла в
том, что площадь под кривой (t ) есть
путь тела за время t.
const
При равномерном движении (
) формула пути имеет вид
S t
16

17.

Принцип
независимости
движения
(действия сил)
dr
Если материальная точка участвует в нескольких
движениях, то ее результирующее перемещение
равно векторной сумме перемещений, обусловленных
каждым из этих движений в отдельности:
d r d r d r ... d r d r d r ,
n
1
2
i
n
i 1
i
17

18.

Так как
Тогда
dr
dt
...
1
2
i
n
.
n
i 1
i
Таким
образом,
скорость
тоже
подчиняется
принципу
независимости
движения.
18

19. 2.3.3. Проекция вектора скорости на оси координат

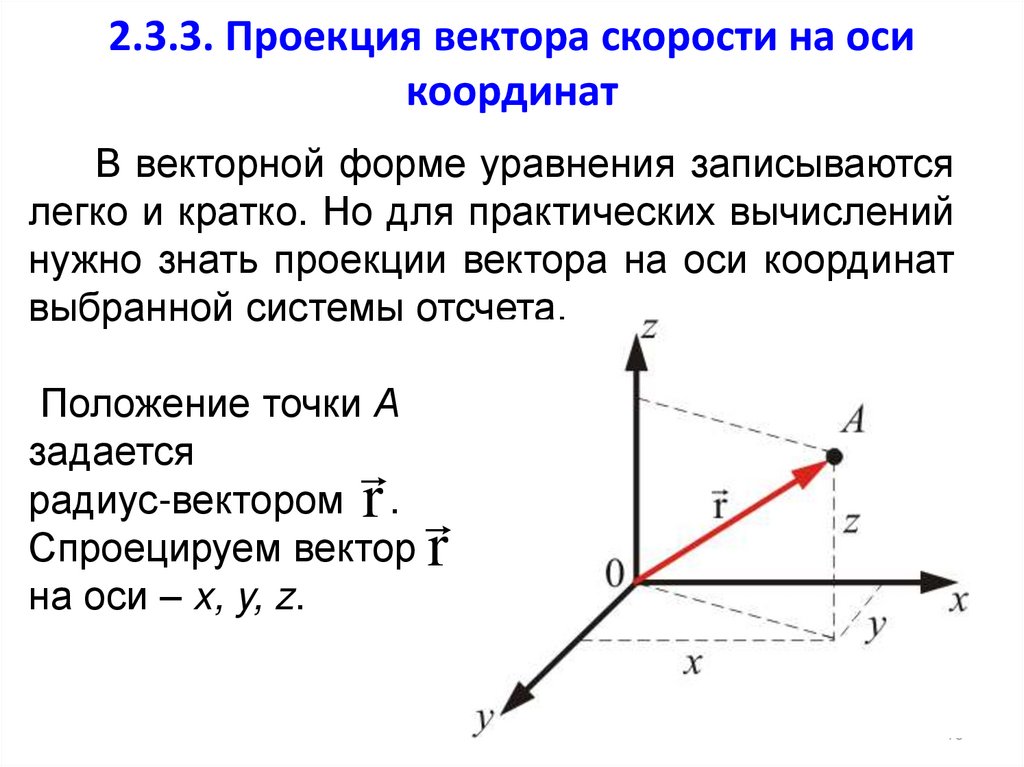
В векторной форме уравнения записываются
легко и кратко. Но для практических вычислений
нужно знать проекции вектора на оси координат
выбранной системы отсчета.
Положение точки А
задается
радиус-вектором r .
Спроецируем вектор r
на оси – x, y, z.
19

20.

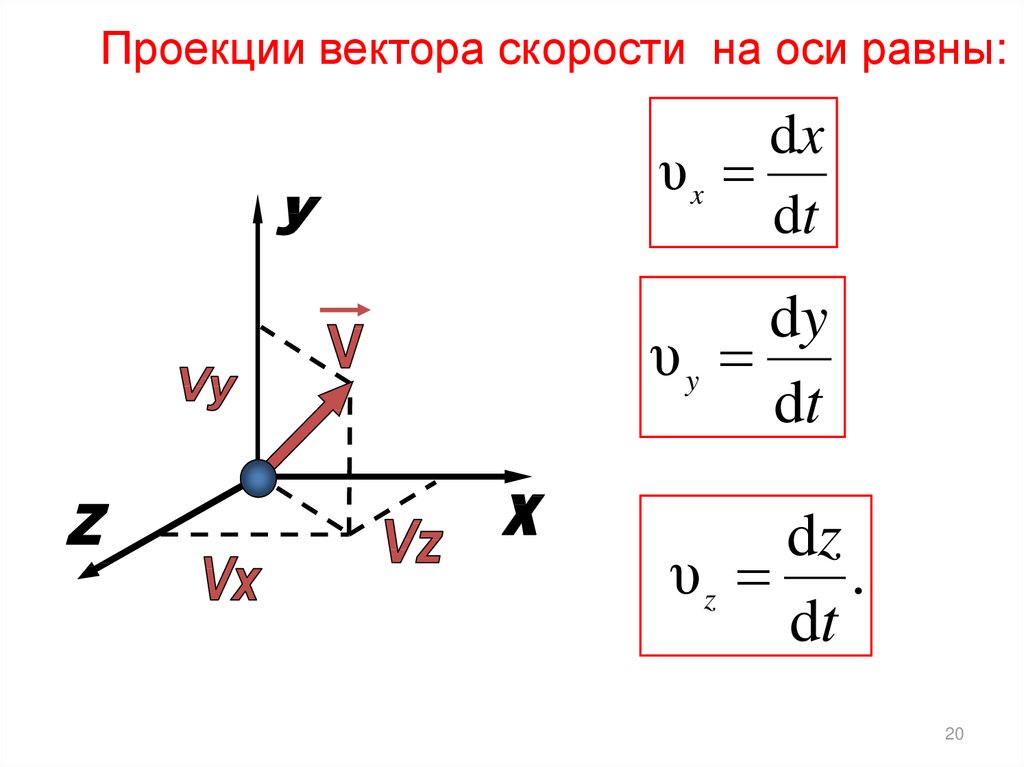
Проекции вектора скорости на оси равны:
dx
υx
dt
dy
υy
dt
dz
υz .
dt
20

21.

Так как
вектор, то
dx dy dz
υ υ x i υ y j υz k
i
j k,
dt
dt
dt
где i, j, k единичные векторы – орты.
υ x i y j z k
Модуль вектора скорости:
2
2
x
y
2
z
21

22. 2.3.4. Ускорение. Нормальное и тангенциальное ускорения

Ускорение это векторная величина, характеризующая
быстроту изменения скорости по модулю и направлению.
Единица измерения ускорения - м/с2.
Среднее
ускорение :
а
t
Мгновенное
ускорение :
d
a im
t 0 t
dt
Ускорение - векторная величина, равная первой производной по
времени от скорости рассматриваемой точки (второй производной по
времени от радиуса-вектора этой же точки).
d d r
a lim
2
t 0 t
dt
dt
Модуль ускорения равен
2
d 2S
a
dt 2
22

23.

Введем единичный вектор τ , связанный с точкой 1 и
направленный по касательной к траектории движения точки 1
и в точке 1
τ
(векторы
совпадают).
Тогда можно записать:
τ,
Где
скорости.
– модуль вектора
23

24.

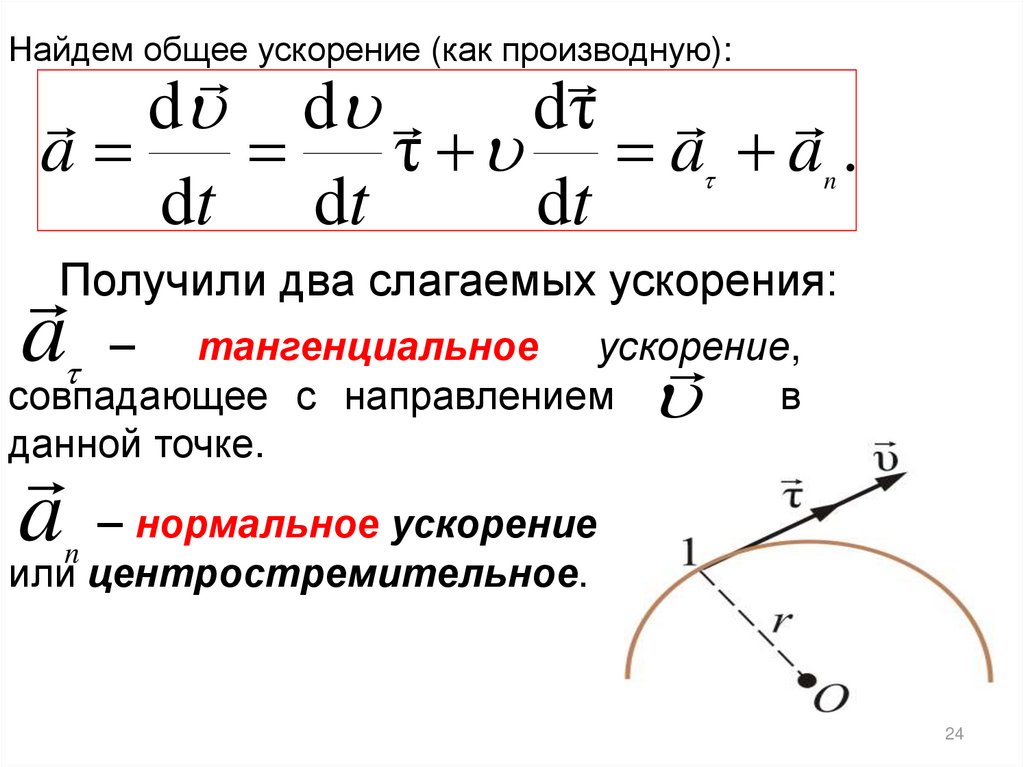
Найдем общее ускорение (как производную):
dτ
d d
a
τ a a .
dt dt
dt
n
Получили два слагаемых ускорения:
a – тангенциальное ускорение,
совпадающее с направлением
в
данной точке.
a – нормальное ускорение
n
или центростремительное.
24

25.

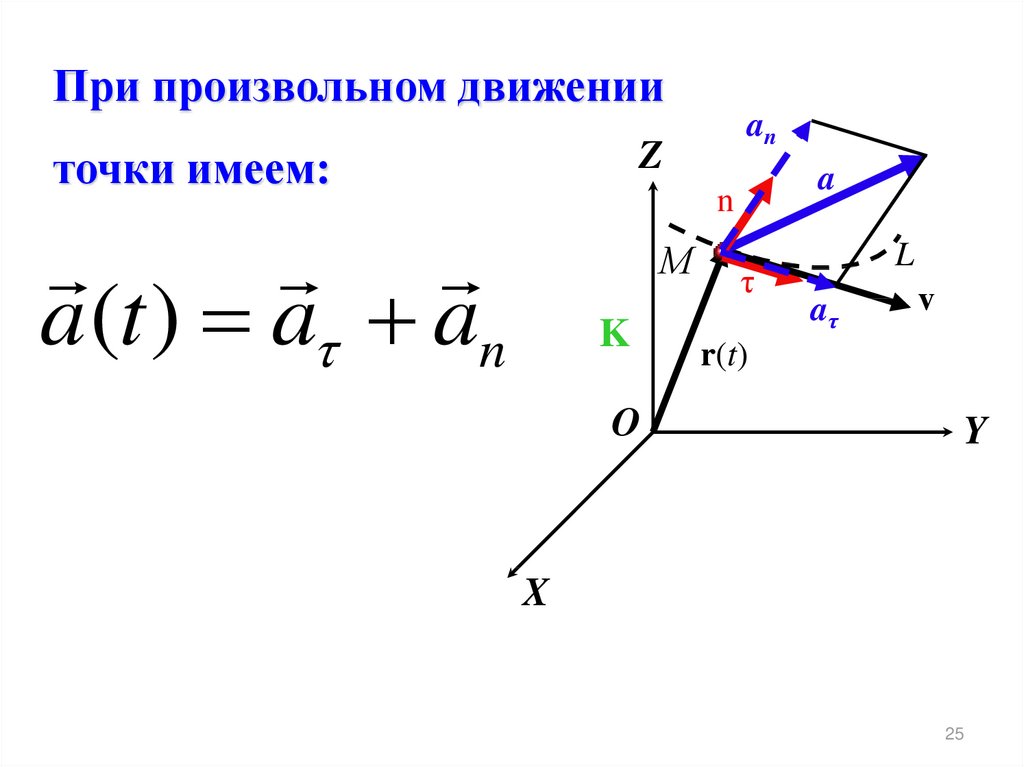
При произвольном движении
an
Z
точки имеем:
a
n
a (t ) a an
М
K
O
τ
L
aτ
v
r(t)
Y
X
25

26.

aτ
d
a
τ
dt
τ
dυ
aτ
dt
-показывает изменение вектора скорости по
d
0
- если
dt
- если
- при
или по модулю
величине:
то a направлено
в ту же сторону, что и
вектор т.е. ускоренное движение;
d
в противоположную
0 то a направлено
dt
d
0
dt
сторону , т.е. замедленное движение;
то aτ 0, const – движение
постоянной по модулю скоростью.
26

27.

Ускорение при произвольном движении
При произвольном движении материальной точки
величина r будет равна радиусу некоторой моментальной (т.е.
соответствующей данному моменту времени) окружности
в
любой
точке
траектории
движение
материальной
точки
можно
рассматривать
как
вращательное движение по окружности,
(с касательным aτ и нормальным an
ускорениями)
r
an
a
a
r an
r
aτ
aτ
Саму величину r называют радиусом кривизны
траектории в данной точке
27

28.

υ
показывает быстроту
a
n
,
изменения направления
r
вектора скорости
Модуль нормального ускорения: a a
.
r
Нормальное ускорение
2
n
2
n
n
Центростремительным называют ускорение –
когда движение происходит по окружности. А
когда движение происходит по произвольной
кривой
–
говорят,
нормальное
ускорение,
перпендикулярное к касательной в любой точке
траектории.
28

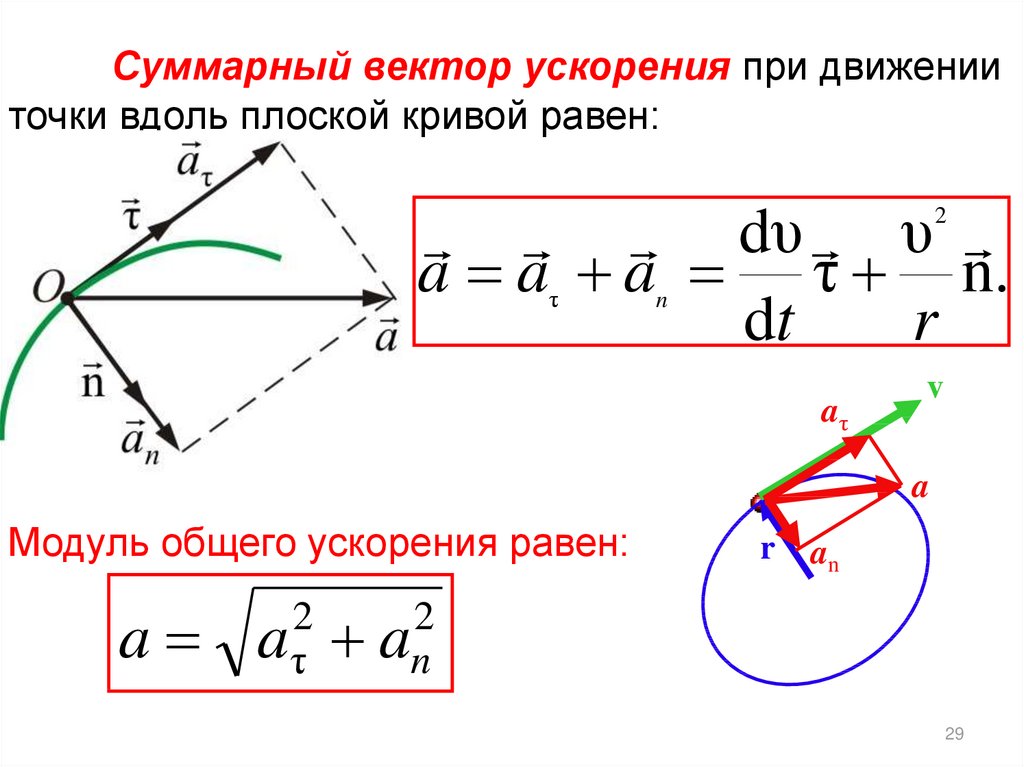
29.

Суммарный вектор ускорения при движении
точки вдоль плоской кривой равен:
dυ υ
a a a τ n.
dt
r
2
τ
n
aτ
v
a
Модуль общего ускорения равен:
a
2
aτ
r
an
2
an
29

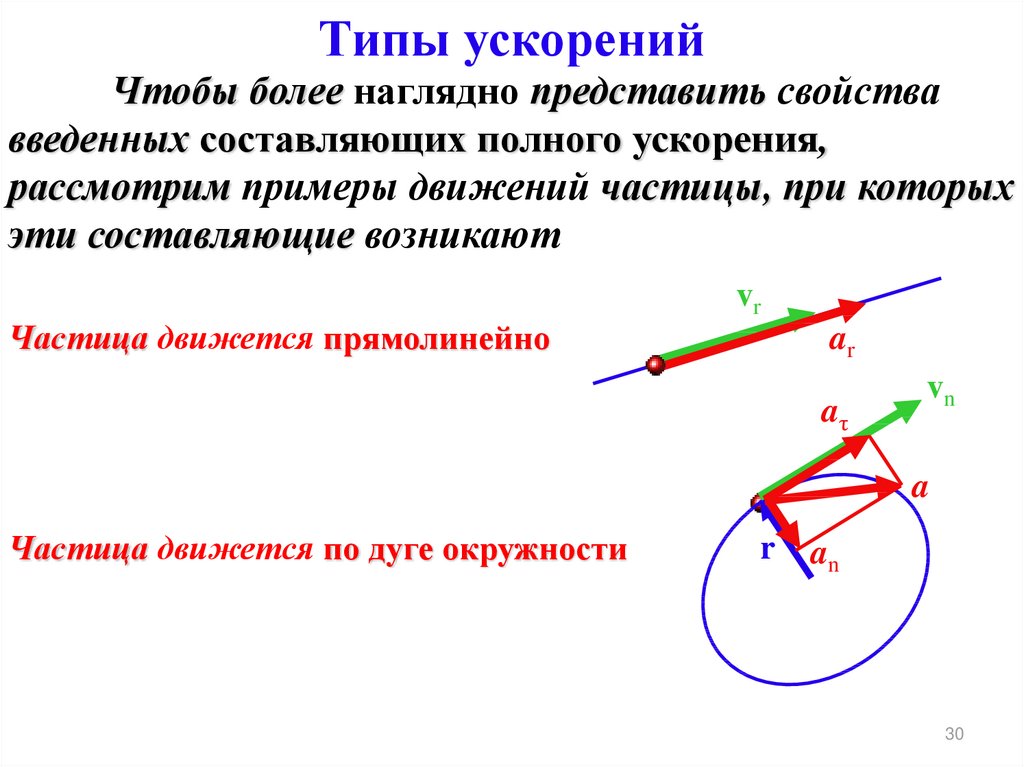
30. Типы ускорений

Чтобы более наглядно представить свойства
введенных составляющих полного ускорения,
рассмотрим примеры движений частицы, при которых
эти составляющие возникают
Частица движется прямолинейно
vr
ar
aτ
vn
a
Частица движется по дуге окружности
r
an
30

31.

При равномерном движении
t
s υdt υt
0
При движении с постоянным ускорением
2
at
S υ 0t
.
2
υ υ0 at
31

32. 2.4. Кинематика твердого тела

Различают пять видов движения твердого
тела:
- поступательное;
- вращательное вокруг неподвижной оси;
- плоское;
- вокруг неподвижной точки;
- свободное.
Поступательное
движение
и
вращательное движение вокруг оси –
основные виды движения твердого тела.
Остальные виды движения твердого тела можно
свести к одному их этих основных видов или к их
32
совокупности.

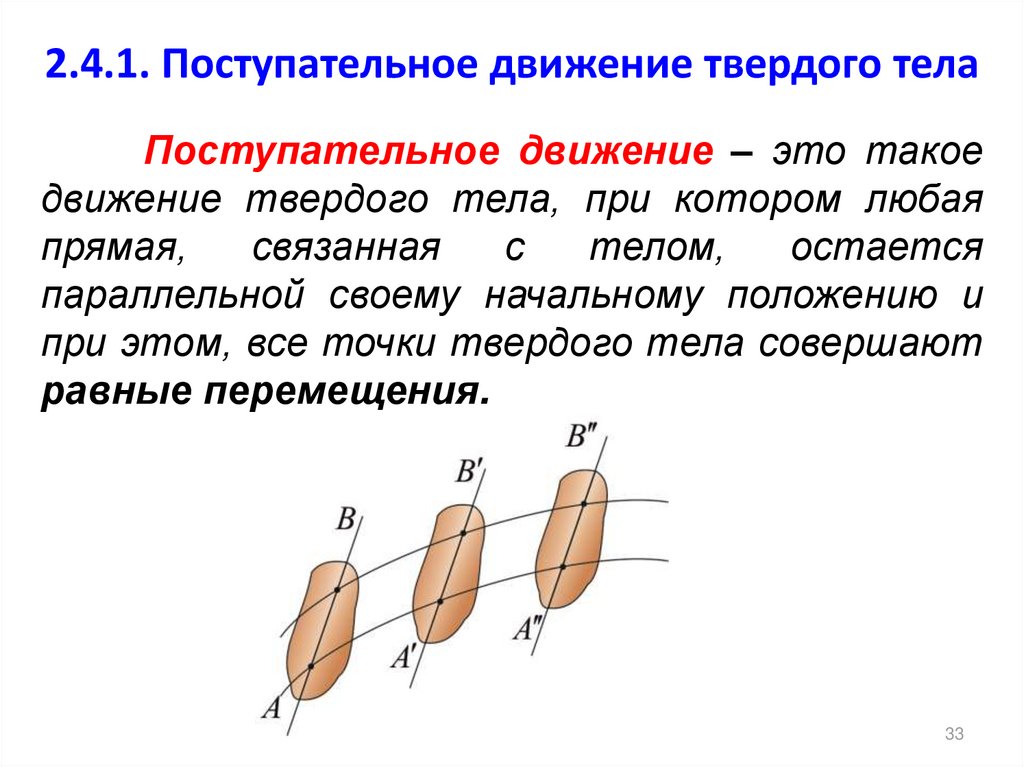
33. 2.4.1. Поступательное движение твердого тела

Поступательное движение – это такое
движение твердого тела, при котором любая
прямая,
связанная
с
телом,
остается
параллельной своему начальному положению и
при этом, все точки твердого тела совершают
равные перемещения.
33

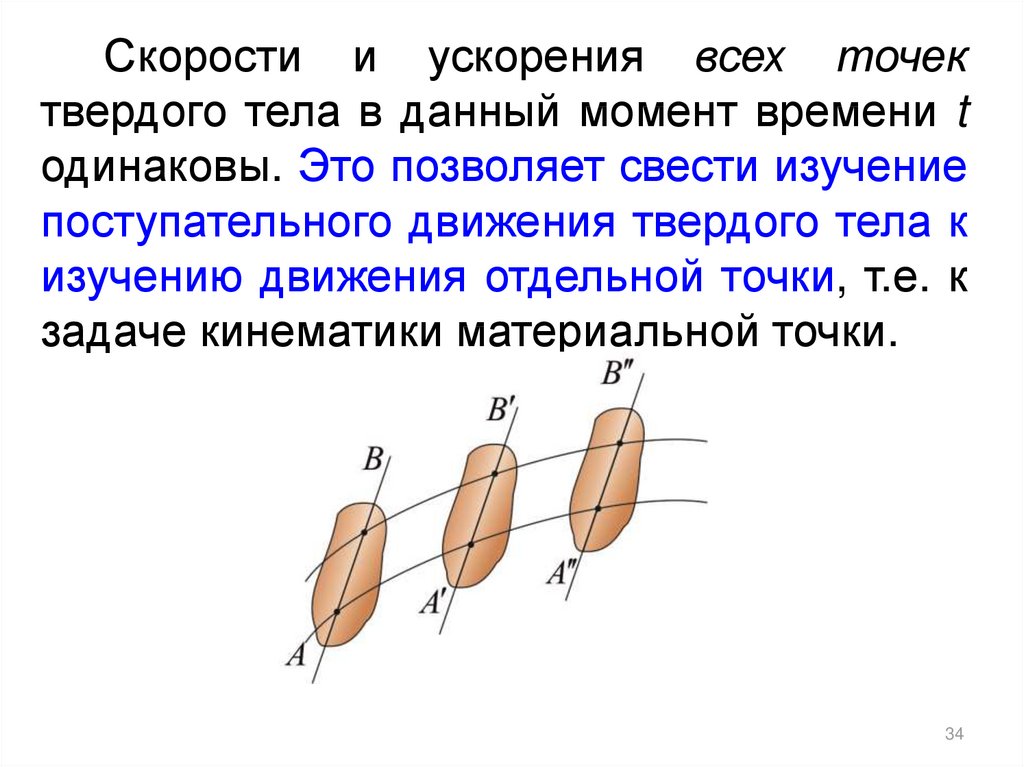
34.

Скорости и ускорения всех точек
твердого тела в данный момент времени t
одинаковы. Это позволяет свести изучение
поступательного движения твердого тела к
изучению движения отдельной точки, т.е. к
задаче кинематики материальной точки.
34

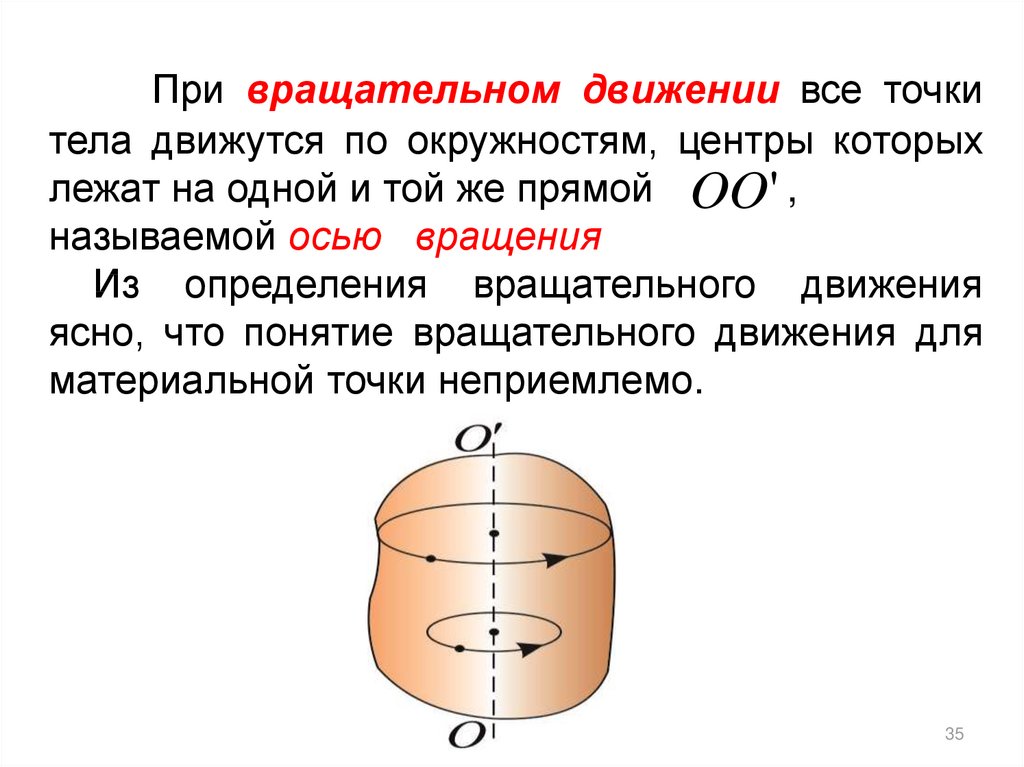
35.

При вращательном движении все точки
тела движутся по окружностям, центры которых
лежат на одной и той же прямой OO' ,
называемой осью вращения
Из определения вращательного движения
ясно, что понятие вращательного движения для
материальной точки неприемлемо.
35

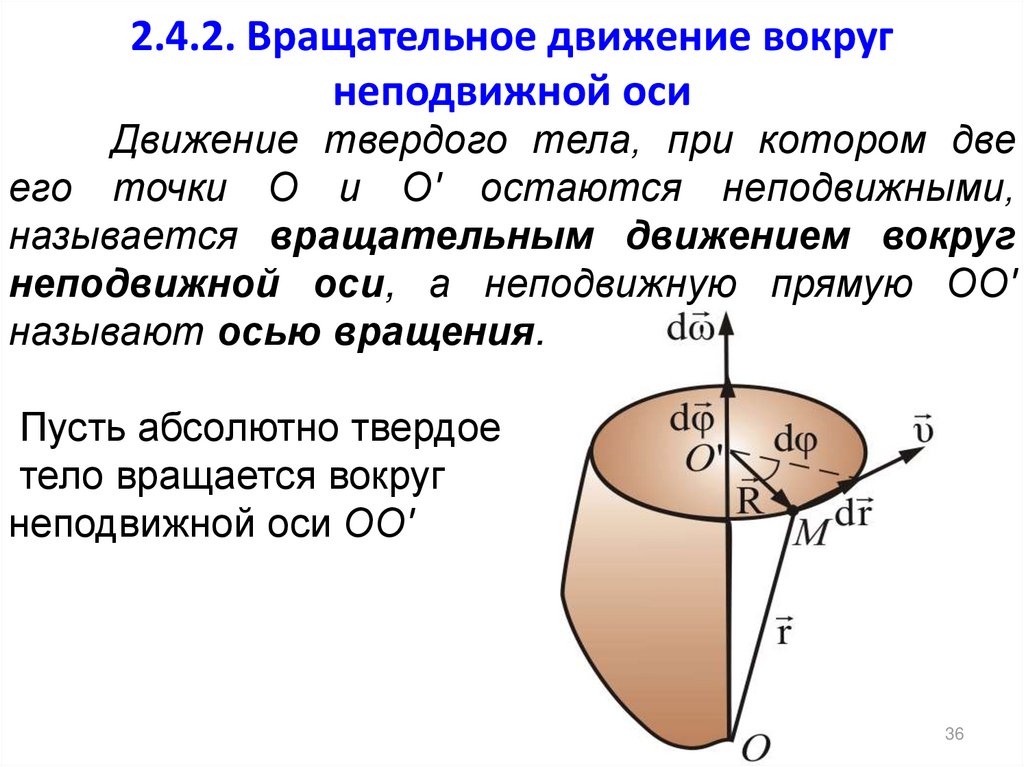
36. 2.4.2. Вращательное движение вокруг неподвижной оси

Движение твердого тела, при котором две
его точки О и О' остаются неподвижными,
называется вращательным движением вокруг
неподвижной оси, а неподвижную прямую ОО'
называют осью вращения.
Пусть абсолютно твердое
тело вращается вокруг
неподвижной оси ОО'
36

37.

Угол поворота dφ характеризует
перемещения всего тела за время dt (угловой путь)
Удобно ввести dφ
численно равный
dφ
– вектор элементарного поворота тела,
и направленный вдоль оси вращения ОО'
dφ
так, чтобы глядя вдоль вектора
мы видели вращение по
часовой стрелке
Направление вектора
и направление вращения связаны правилом буравчика.
dφ
37

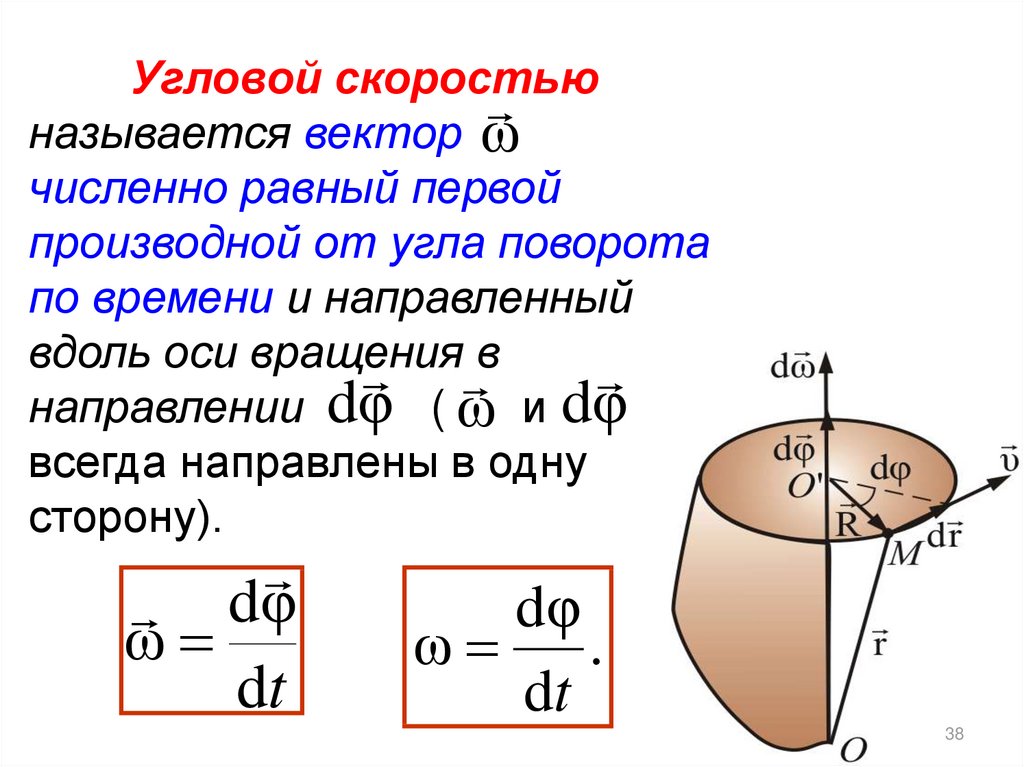
38.

Угловой скоростью
называется вектор ω
численно равный первой
производной от угла поворота
по времени и направленный
вдоль оси вращения
в
направлении dφ ( ω и dφ
всегда направлены в одну
сторону).
dφ
ω
dt
dφ
ω .
dt
38

39.

Связь линейной и угловой скорости
Пусть – линейная скорость точки М.
За промежуток времени dt точка М проходит
путь dr dt.
В
то
же
время
dr Rdφ (центральный угол). Тогда,
dr Rdφ
υ
dt
dt
ωR
υ ωR
υ [ω, R ]
39

40.

Период Т – промежуток времени, в
течение которого тело совершает полный
оборот (т.е. поворот на угол φ 2π )
Частота
2π
Т ;
ω
n – число оборотов тела за 1 сек.
1
n .
Т
Угловая скорость
2π
ω 2πn;
Т
40

41.

ε
Введем вектор углового ускорения
для характеристики неравномерного вращения
тела:
dω
ε
dt
ε направлен в ту же
Вектор
сторону, что и ω при ускоренном
вращении
dω
ε
0
dt
а
направлен
в противопо
ложную сторону при замедленном
вращении
dω
0
dt
41

42.

Выразим
нормальное
и
тангенциальное
ускорения точки М через угловую скорость и угловое
ускорение:
dυ d
dω
aτ
(ωR) R
Rε;
dt dt
dt
a R ;
υ
2
an
ω R.
R
2
42

43.

Формулы простейших случаев вращения тела
вокруг неподвижной оси:
ω const;
- равномерное вращение ε 0;
φ φ0 ωt ;
- равнопеременное
вращение
ε const ;
ω ω 0 εt
εt
φ ω 0t
2
2
43

44.

Связь между линейными и угловыми
величинами при вращательном движении:
s Rφ
υ R ω
a a τ an
a
2
aτ
2
an
an υ R ω R
2
2
aτ R ε.

45.

45

46.

Базовая литература
[1] Трофимова Т.И. Курс физики: Учеб.
пособие для вузов. М.: Академия, 2004.- 560с.
Дополнительная литература
[7] Сулеева Л.Б. Электронный учебник.
Физика, часть 1” Механика. Молекулярная
физика и термодинамика” Изд. КазНТУ, 2006.
[2] Трофимова Т.И., Павлова З.Г. Сборник
[8] Трофимова Т.И. Физика: 500 основных
задач по курсу физики с решениями: Учебное
законов и формул: Справочник для студентов
пособие для вузов. Изд. 2– е, испр./ 3– е – 591с. М:
вузов. Изд. 3– е – 63 с. М: Высшая Школа, 1999.
Высшая Школа, 2002.
[3] Савельев И.В. Курс общей физики: Учеб.
пособие для втузов: В 5 кн.: Кн.1:
Механика. Молекулярная физика. М.:
Астрель, 2005. – 312 с.
[9]Волькенштейн В.С. Сборник задач по общему
курсу физики для студентов
технических вузов Изд. доп., перераб. - 327 с.
{Специалист} СПб: СпецЛит, 2002.
[4] Грабовский Р.И. Курс физики: Учебник
для вузов. Изд. 6-е - 608 с. {Учебники для вузов:
Специальная литература}, СПб: Лань, 2002.
[10] Чертов А., Воробьев А. Задачник по
физике. – М.: Высшая школа, 1981.
[5] Детлаф А.А., Яворский Б.М. Курс
физики: Учебное пособие для втузов. Изд. 6-е,
испр. - 607 с. М: Высшая Школа, 2003.
[6] Савельев И.В. Курс общей физики: Учеб.
пособие для втузов: В 5 кн.: Кн. 2: Электричество
и магнетизм. М.: АСТ: Астрель, 2005. – 336 с.
46