Теоретическая механика

1. Теоретическая механика

2. КИНЕМАТИКА ТОЧКИ И ТВЁРДОГО ТЕЛА

2.

Тема 9.
КИНЕМАТИКА ТОЧКИ
9.1. ВВЕДЕНИЕ В КИНЕМАТИКУ.
Кинематикой называется раздел
механики, в котором изучаются
геометрические свойства движения тел без
учёта их инертности (массы) и действующих
на них сил.
Под движением мы понимаем в механике
изменение с течением времени положения
данного тела в пространстве по отношению к
другим телам.
2

3.

9.1. ВВЕДЕНИЕ В КИНЕМАТИКУ.
Движение тел совершается в пространстве с течением
времени.
Пространство в механике мы рассматриваем как
трёхмерное евклидово пространство.
За единицу длины при измерении расстояний
принимается 1 м.
Время в механике считается универсальным, т. е.
протекающим одинаково во всех рассматриваемых
системах отсчёта. За единицу времени принимается 1 с.
Время является скалярной, непрерывно изменяющейся величиной. В задачах
кинематики время t принимают за независимое переменное. Все другие
переменные величины (расстояния, скорости и т. д;) рассматриваются как
изменяющиеся стечением времени, т. е. как функции времени t. Отсчёт времени
ведётся от некоторого начального момента (t = 0). Всякий данный момент
времени t определяется числом секунд, прошедших от начального момента до
данного. Разность между какими-нибудь двумя последовательными моментами
времени называется промежутком времени.
3

4.

9.1. ВВЕДЕНИЕ В КИНЕМАТИКУ.
Кинематически задать движение или закон
движения тела (точки) — значит задать положение
этого тела (точки) относительно данной системы
отсчёта в любой момент времени.
Основная задача кинематики точки и твёрдого тела
состоит в том, чтобы, зная закон движения точки
(тела), установить методы определения всех
кинематических величин, характеризующих данное
движение.
Непрерывная линия, которую описывает движущаяся
точка относительно данной системы отсчёта,
называется траекторией точки. Если траекторией
является прямая линия, движение точки называется
прямолинейным, а если кривая — криволинейным.
4

5.

9.2. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ.
Для задания движения точки можно применять один из
следующих трёх способов:
1) векторный,
2) координатный,
3) естественный.
1. Векторный способ задания движения точки.
Положение этой точки в любой момент
времени можно определить, задав её
радиус-вектор r, проведённый из начала
координат О в точку М.
Зависимость r = r(t) – это закон
движения точки в векторной форме.
Аналитически вектор задаётся его
r r t ,
проекциями на координатные оси. В
прямоугольных декартовых координатах
r xi yj zk .
для вектора r будет:

6.

9.2. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ.
2. Координатный способ задания движения точки
Положение точки можно непосредственно определять её
декартовыми координатами х, у, z, которые при движении
точки будут с течением времени изменяться.
Чтобы знать закон движения точки, т. е. её положение в
пространстве в любой момент времени, надо знать значения
координат точки для каждого момента времени.
x f1 t , y f 2 t , z f 3 t .
Эти уравнения представляют собой уравнения движения
точки в прямоугольных декартовых координатах.
Если движение точки
происходит все время в одной и
той же плоскости, то получим
два уравнения движения:
x f1 t , y f 2 t .
При прямолинейном движении
точки, если вдоль её траектории
направить координатную ось Ох,
движение будет определяться
одним уравнением :
x f1 t .
6
6

7.

9.2. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ.
3. Естественный способ задания движения точки
Естественным (или траекторным) способом
задания движения удобно пользоваться в
тех случаях, когда траектория движущейся
точки известна заранее.
Пусть кривая АВ является траекторией
точки М при её движении относительно
системы отсчёта Охуz. Тогда положение
точки М на траектории будет однозначно определяться
криволинейной координатой s, которая равна расстоянию от
точки О’ до точки М, измеренному вдоль дуги траектории и
взятому с соответствующим знаком.
Чтобы задать положение точки М на траектории в любой
момент времени, надо знать зависимость,
которая называется закон движения точки М
вдоль траектории.
7
s f t .
7

8.

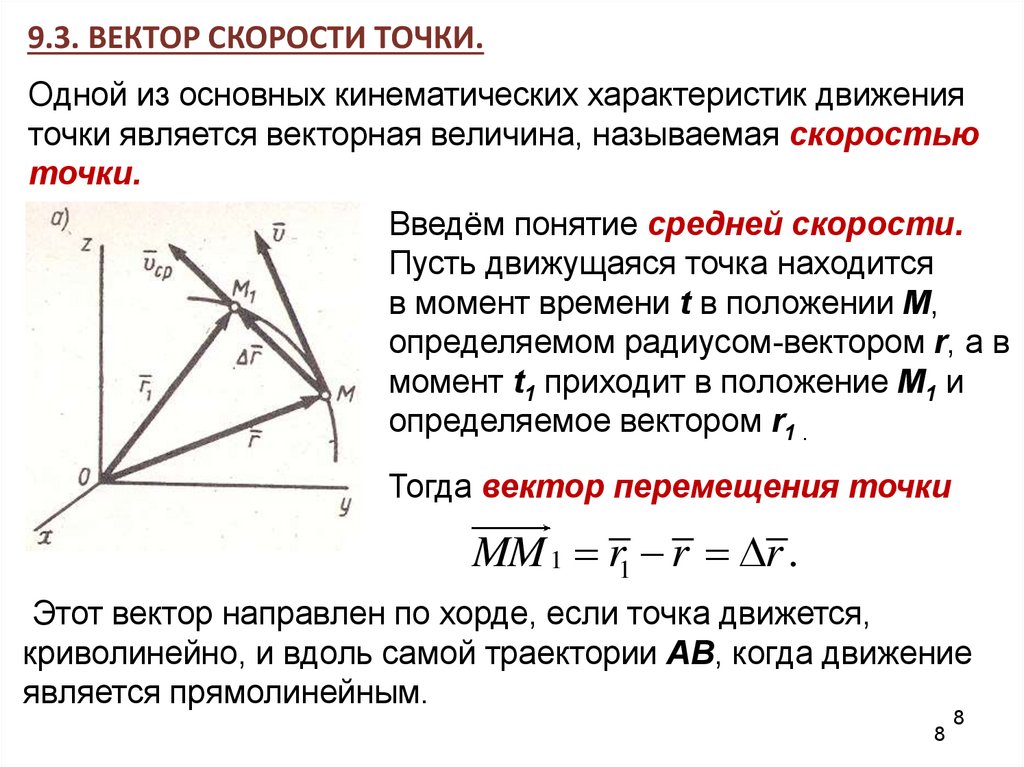
9.3. ВЕКТОР СКОРОСТИ ТОЧКИ.
Одной из основных кинематических характеристик движения
точки является векторная величина, называемая скоростью
точки.
Введём понятие средней скорости.
Пусть движущаяся точка находится
в момент времени t в положении М,
определяемом радиусом-вектором r, а в
момент t1 приходит в положение М1 и
определяемое вектором r1 .
Тогда вектор перемещения точки
MM 1 r1 r r .
Этот вектор направлен по хорде, если точка движется,
криволинейно, и вдоль самой траектории АВ, когда движение
является прямолинейным.
8
8

9.

9.3. ВЕКТОР СКОРОСТИ ТОЧКИ.
Отношение вектора перемещения точки к
соответствующему промежутку времени даёт
векторную величину, называемую средней по
модулю и направлению скоростью точки за
промежуток времени t:
MM 1 r
vср
.
t
t
Направлен вектор ср так же, как и вектор MM1, т. е. при
криволинейном движении вдоль хорды в сторону движения
точки, а при прямолинейном движении — вдоль самой
траектории.
9

10.

9.3. ВЕКТОР СКОРОСТИ ТОЧКИ.
Чтобы получить точную характеристику движения, вводят
понятие о скорости точки данный момент времени.
Скоростью точки в данный момент времени t
называется векторная величина , к которой
стремится средняя скорость ср при стремлении
промежутка времени t к нулю:
r
dr
v lim vср lim
или v
.
t 0
t 0 t
dt
Вектор скорости точки в данный момент времени
равен первой производной от радиуса-вектора
точки по времени.
Вектор скорости точки в данный момент времени
направлен по касательной к траектории точки в
сторону движения.
10

11.

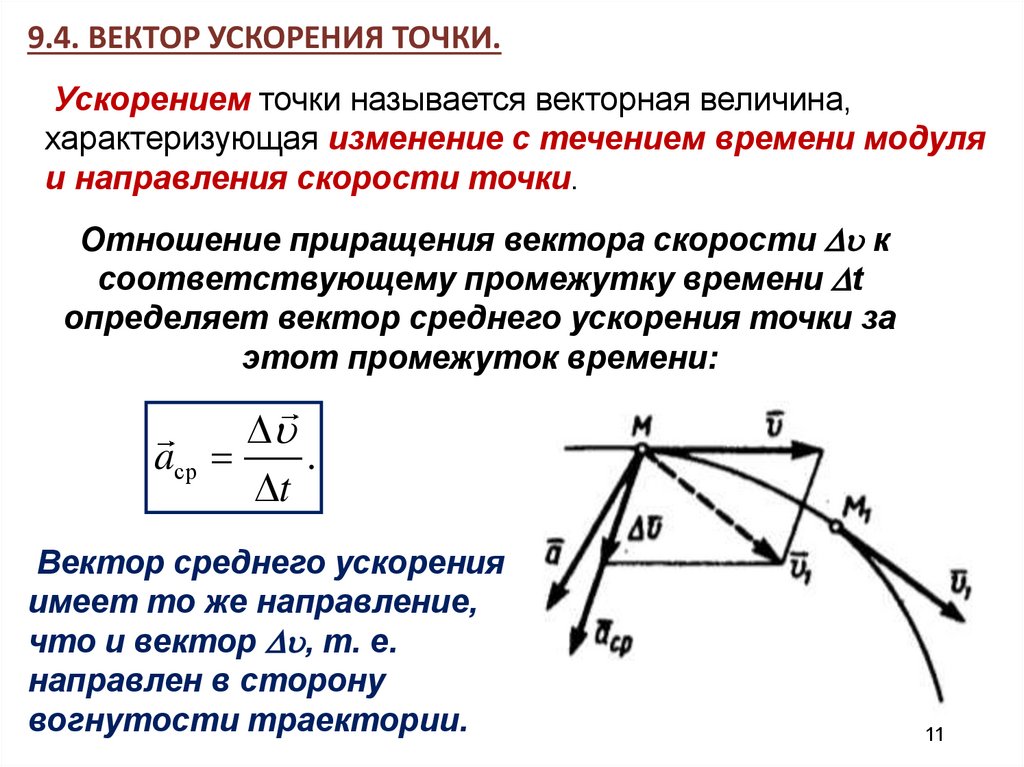
9.4. ВЕКТОР УСКОРЕНИЯ ТОЧКИ.
Ускорением точки называется векторная величина,
характеризующая изменение с течением времени модуля
и направления скорости точки.
Отношение приращения вектора скорости к
соответствующему промежутку времени t
определяет вектор среднего ускорения точки за
этот промежуток времени:
aср
.
t
Вектор среднего ускорения
имеет то же направление,
что и вектор , т. е.
направлен в сторону
вогнутости траектории.
11

12.

9.4. ВЕКТОР УСКОРЕНИЯ ТОЧКИ.
Ускорением точки в данный момент времени t
называется векторная величина, к которой стремится
среднее ускорение, при стремлении промежутка
времени t к нулю:
v dv
a lim
.
t 0 t
dt
dv d 2 r
a
2.
dt dt
Следовательно, вектор ускорения точки в данный
момент времени равен первой производной от вектора
скорости или второй производной от радиуса-вектора
точки по времени.
При прямолинейном движении вектор а направлен вдоль прямой, по
которой движется точка.
Если траекторией точки является плоская кривая, то вектор ускорения
а, так же как и вектор аср, лежит в плоскости этой кривой и направлен в
12
12
сторону её вогнутости.

13.

9.5. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ
КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ.
9.5.1. Определение скорости точки
Проекции скорости точки на координатные оси равны
первым производным от соответствующих координат
точки по времени.
dx
dy
dz
vx , v y , vz
или vx x, v y y, vz z.
dt
dt
dt
Зная проекции скорости, найдём её модуль и
направление (т. е. углы , , , которые вектор а
образует с координатными осями) по формулам
vy
vx
vz
cos , cos , cos .
v
v
v
v vx2 v 2y vz2 ;
13
13

14.

9.5. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ
КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ.
9.5.2. Определение ускорения точки
Проекции ускорения точки на координатные оси равны
первым производным от проекций скорости или
вторым производным от соответствующих
координат точки по времени.
dv y d 2 y
dvx d 2 x
dvz d 2 z
ax
2 , ay
2 , az
2 или
dt
dt
dt
dt
dt
dt
a x v x x, a y v y y , a z v z z .
14
14

15.

9.5. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ
КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ.
9.5.2. Определение ускорения точки
Модуль и направление ускорения найдутся из формул
где 1, 1, 1 - углы, образуемые вектором ускорения с
координатными осями.
ay
ax
az
cos 1 , cos 1 , cos 1 .
a
a
a
a ax2 a 2y az2 ;
В случае прямолинейного движения, которое задаётся
одним уравнением x = f(t), будет
d x d 2 x
dx
x , ax
2
dt
dt
dt
15

16.

9.6. КАСАТЕЛЬНОЕ И НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ.
Проекция ускорения точки а на касательную равна
первой производной от числового значения скорости
или второй производной от расстояния по времени.
2
dv d s
a
2
dt dt
А проекция ускорения аn на главную нормаль равна
квадрату скорости, делённому на радиус кривизны
траектории в данной точке кривой.
an .
2
Величины а и аn называют касательным и нормальным
ускорениями точки.
16
16

17.

9.6. КАСАТЕЛЬНОЕ И НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ.
Отложим вдоль касательной М и главной нормали Мn
векторы а , и аn, т. е. касательную и нормальную
составляющие ускорения.
- Cоставляющая аn
будет всегда
направлена в. сторону
вогнутости кривой.
Вектор ускорения точки а
изображается диагональю
параллелограмма- построенного на
составляющих а и аn.
a
a
2
2
an a ; tg .
an
- составляющая а ,
может быть
направлена или в
положительном, или в
отрицательном
направлении оси М в
зависимости от знака
проекции а .
17

18. Задача 1. Движение точки задано уравнениями: x = 8t - 4t2, y = 6t - 3t2. Определить траекторию, скорость и ускорение точки.

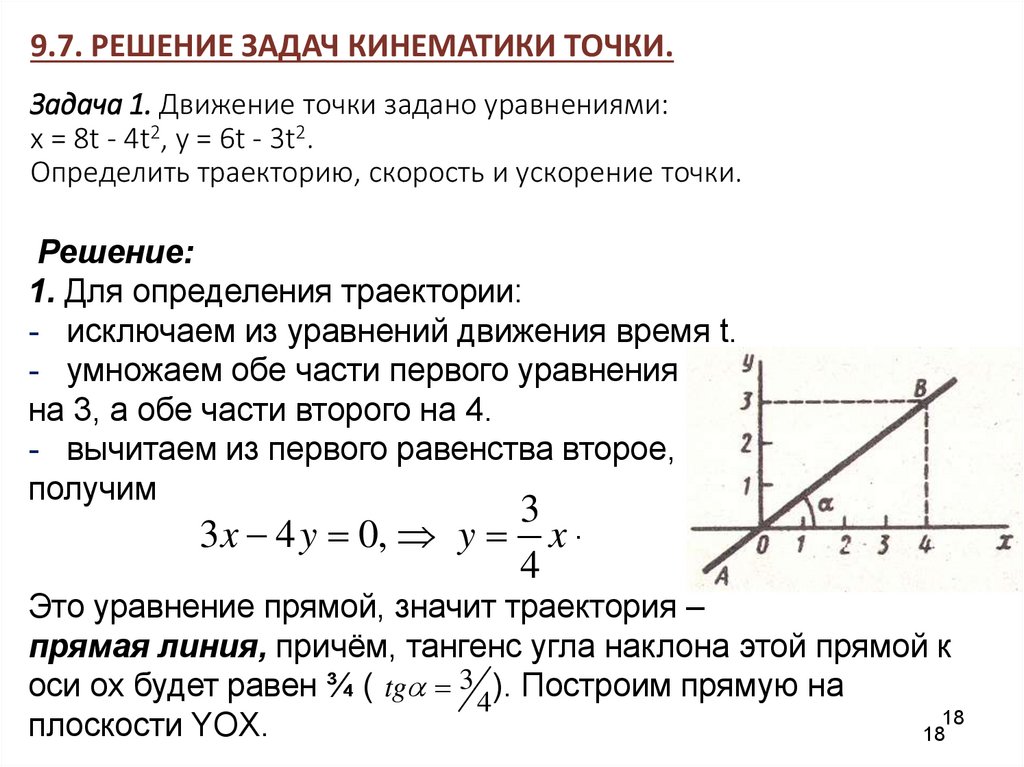
9.7. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ.
Задача 1. Движение точки задано уравнениями:
x = 8t - 4t2, y = 6t - 3t2.
Определить траекторию, скорость и ускорение точки.
Решение:
1. Для определения траектории:
- исключаем из уравнений движения время t.
- умножаем обе части первого уравнения
на 3, а обе части второго на 4.
- вычитаем из первого равенства второе,
получим
3 .
3 x 4 y 0, y x
4
Это уравнение прямой, значит траектория –
прямая линия, причём, тангенс угла наклона этой прямой к
оси ох будет равен ¾ ( tg 3 4). Построим прямую на
18
плоскости YOX.
18

19.

9.6. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ.
Решение:
2. Пользуясь определением величины, найдём скорость точки:
vx x 8(1 t ), v y y 6(1 t );
v vx2 v 2y 10 1 t .
3. Теперь найдём ускорение точки (тоже пользуясь
определением физической величины):
ax x 8, a y y 6, a 10м/с2 .
Направлены векторы и а вдоль
траектории, т. е. вдоль прямой АВ.
Проекции ускорения на координатные
оси все время отрицательны,
следовательно, ускорение имеет
постоянное направление от В к А.
19

20. Задача 2. Движение точки задано уравнениями: Определить траекторию, скорость и ускорение точки.

Задача 2. Движение точки задано уравнениями:
x R sin t , y R cos t , z ut
Определить траекторию, скорость и ускорение точки.
Решение:
1. Возведём первые два уравнения в квадрат
и складывая, получаем
2
2
2 .
x y R
Следовательно, траектория лежит на
круглом цилиндре радиусом R, ось которого
направлена вдоль оси ОZ.
2. Определяя из последнего уравнения t и
подставляя в первое
x R sin z / u
Таким образом, траекторией точки будет
винтовой линией.
20
20

21.

Решение:
3. Из уравнений движения видно, что один виток винтовой
линии точка проходит за время
t1
2
.
При этом вдоль оси z точка за это время перемещается на
величину равную шагу винтовой линии
h ut1
2 u
.
4. Найдём скорость точки. Дифференцируя уравнения
движения по времени, получаем:
vx x R cos t , v y y R sin t ;
v R 2 2 cos 2 t sin 2 t u 2 R 2 2 u 2
Движение происходит с постоянной по модулю скоростью,
направленной по касательной к траектории.
21

22.

Решение:
5. Найдём ускорение точки. Дифференцируя уравнения
изменения скорости по времени, получаем:
ax vx R 2 sin t ,
a y v y R cos t ,
2
az vz 0,
a
2
2
2
ax a y R .
Движение происходит с постоянным по модулю ускорением.
22