Similar presentations:
Статика, кинематика. Экзамен по теоретической механике
1. Новосибирский Государственный Архитектурно- Строительный Университет (Сибстрин)
Новосибирский Государственный АрхитектурноСтроительный Университет (Сибстрин)ПРОГРАММА
по теоретической механике для
бакалавров (направление строительство)
(2-й семестр) на 2013 г.
Составитель:
докт. физ.-мат. наук, профессор
Рудяк Валерий Яковлевич
Кафедра теоретической механики
2
2. Экзамен по теоретической механике
На экзамен выносится два раздела:• статика
• кинематика
1.1. ВВЕДЕНИЕ
2
3. I. Статика
I.1. Аксиомы статики3
4. 1.1. Аксиомы статики
Задачи статики
Основные модели в механике: материальная точка, ТТ,ДТ
Сила
Система сил
Равные силы
Эквивалентные системы сил
Уравновешенная система сил
Аксиомы статики
Определение связи
Сила реакции связи
Типы связей
Аксиома связей
I. СТАТИКА
4
5. 1.1.1. Основные задачи статики
• Первая задача состоит в замене данной системысил, приложенных к твердому телу,
эквивалентной системой сил
• Вторая задача заключается в формулировании
условий равновесия тела под действием данной
системы сил
• Есть и другие: (i) определение условий
устойчивости движения или равновесия;
(ii) определение возможных положений равновесия;
и т.д.
1.1. АКСИОМЫ СТАТИКИ
5
6. 1.2. Основные модели механики
• Любой объект (тело) можно моделироватьматериальной точкой, если его внутренней
структурой можно пренебречь, а расстояние L до
него много больше его размеров R: L >> R
• Любое тело можно моделировать системой
взаимодействующих материальных точек
j
i
• Твердое тело – система взаимодействующих материальных
точек, расстояние между
которыми не меняется
со временем: rij (t) = const
1.2.
1.2. АКСИМЫ
ОСНОВНЫЕ СТАТИКИ
ПОНЯТИЯ И МОДЕЛИ
6
7. 1.1.2. Основные модели механики
• Деформируемое тело – система взаимодействующихматериальных точек, расстояние между которыми
с течением времени меняется
• Деформируемое тело можно моделировать твердым
на временах t << T, где Т – время деформации
• Механическая система – совокупность
взаимодействующих или свободных материальных
точек или тел
1.1.
СТАТИКИ
1.2. АКСИОМЫ
ОСНОВНЫЕ ПОНЯТИЯ
И МОДЕЛИ
7
8. 1.1.3. Сила
Сила – величина, характеризующая меру взаимодействияматериальных объектов (тел)
Силы возникают
• при непосредственном контакте тел (точечные и
распределенные силы)
• при наличии силовых полей (действуют в каждой точке
пространства)
• Сила – векторная величина. Ее
действие характеризуется
F
модулем, точкой приложения
M
А
и направлением
• Прямая, вдоль которой направL
лена сила (LM), называется
линией действия силы
1.2.
СТАТИКИ
1.2. АКСИОМЫ
ОСНОВНЫЕ ПОНЯТИЯ
И МОДЕЛИ
8
9. 1.1.4. Система сил
• Совокупность нескольких сил, (F1, F2 ,..., Fn ) , называетсясистемой сил
• Если действие на тело системы сил (F1, F2 ,..., Fn ) можно
заменить действием другой системы (P1, P1,..., Pk ) , то такие
системы сил называются эквивалентными
• Если система сил эквивалентна одной силе (F1, F2 ,..., Fn ) ~ R,
то последняя называется равнодействующей
• Две одинаково направленные силы, приложенные к
одной точке и равные по модулю, называются равными
• Система сил называется уравновешенной (эквивалент
ной нулю) ( F1, F2 ,..., Fn ) ~ 0, если под ее действием тело
покоится или равномерно и прямолинейно двигается
1.1.
СТАТИКИ
1.2. АКСИОМЫ
ОСНОВНЫЕ ПОНЯТИЯ
И МОДЕЛИ
9
10. Аксиома 1. Равновесие тела под действием двух сил
Твердое тело находится в равновесии под действиемдвух сил тогда и только тогда, когда эти силы равны по
модулю и противоположно направлены (линии действия
при этом совпадают)
F2
В
F1
M
А
L
Эта аксиома определяет простейшую уравновешенную
систему сил, т.е. систему сил, эквивалентную нулю
( F1; F2 ) ~ 0
1.3.АКСИОМЫ
СТАТИКИ
1.1.
СТАТИКИ
1.2. АКСИОМЫ
ОСНОВНЫЕ
ПОНЯТИЯ
И МОДЕЛИ
10
11.
Аксиома 2. О добавлении уравновешенной системы силДействие данной системы сил на твердое тело не
изменится, если к ней прибавить или отнять
уравновешенную систему сил
Следствие из 1-й и 2-й аксиом
Точку приложения силы можно переносить
вдоль линии ее действия
Доказательство
• Приложим систему сил ( F1 , F2 ) ~ 0
• Пусть F1 F2 F и их линии
действия совпадают
А2
F2
В
F1
F
M
А
L
А2
F ~ ( F ,0) ~ ( F , ( F1 , F2 )) ~ (( F , F2 ), F1 ) ~ (0, F1 ) ~ F1
1.3.
АКСИОМЫ СТАТИКИ
1.1.
СТАТИКИ
1.2. АКСИОМЫ
ОСНОВНЫЕ
ПОНЯТИЯ
И МОДЕЛИ
А1
11
12.
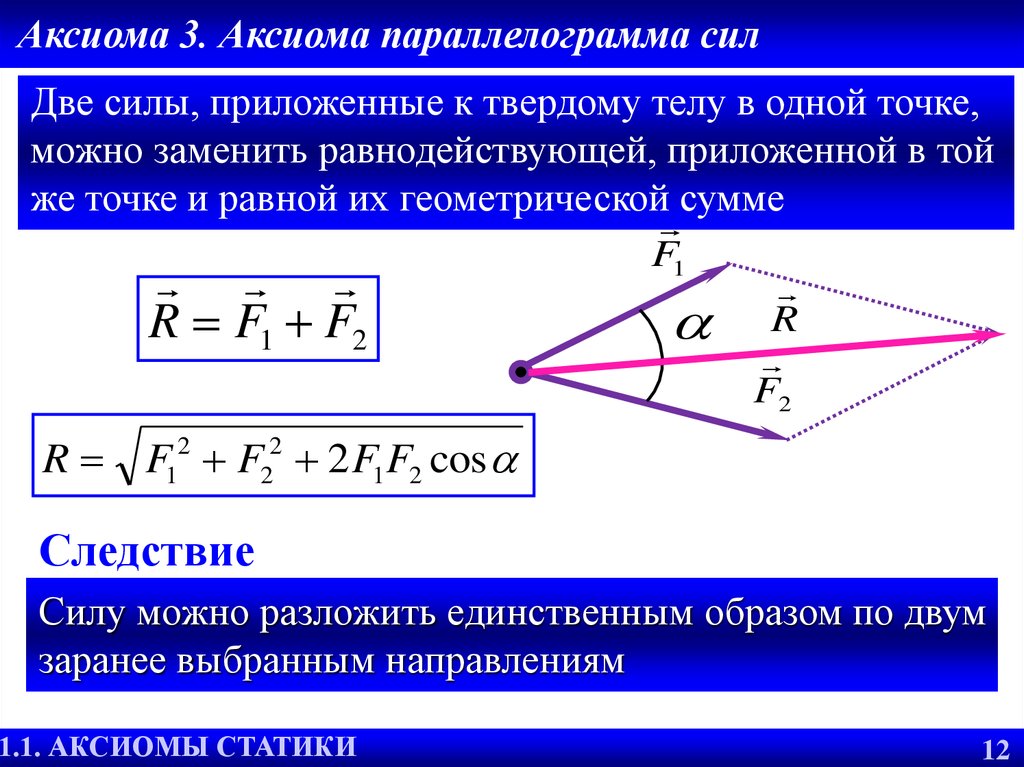
Аксиома 3. Аксиома параллелограмма силДве силы, приложенные к твердому телу в одной точке,
можно заменить равнодействующей, приложенной в той
же точке и равной их геометрической сумме
R F1 F2
F1
R
F2
R F F 2 F1F2 cos
2
1
2
2
Следствие
Силу можно разложить единственным образом по двум
заранее выбранным направлениям
1.3.
АКСИОМЫ СТАТИКИ
1.1.
СТАТИКИ
1.2. АКСИОМЫ
ОСНОВНЫЕ
ПОНЯТИЯ
И МОДЕЛИ
12
13. Аксиома 4. Третий закон Ньютона
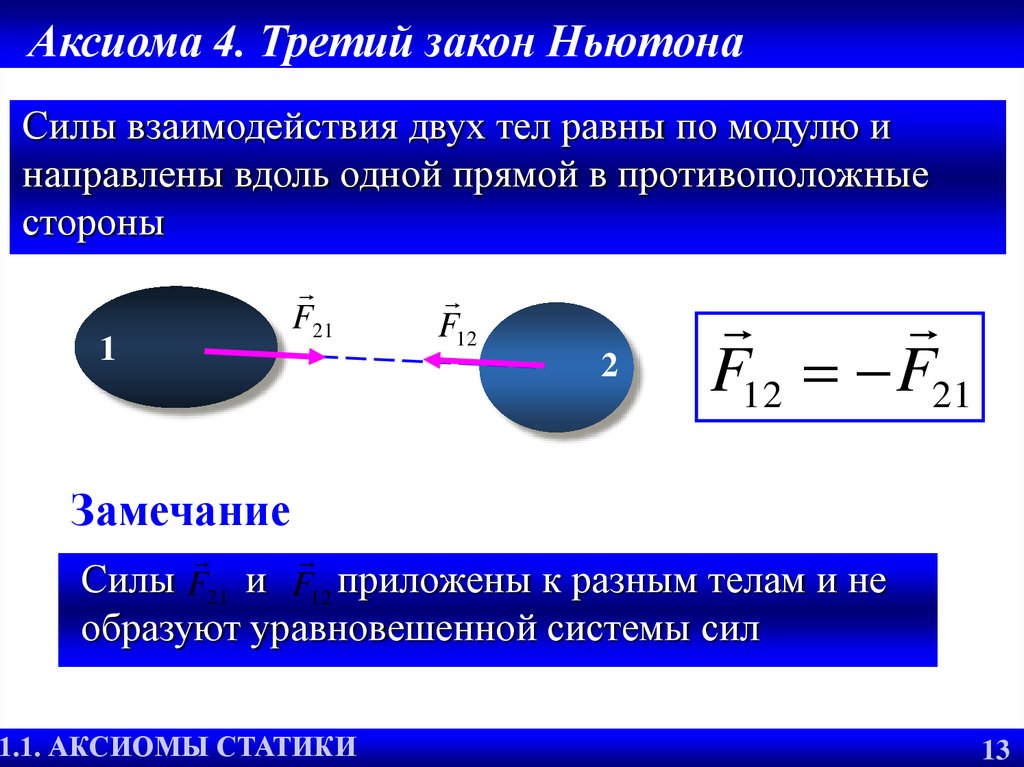
Силы взаимодействия двух тел равны по модулю инаправлены вдоль одной прямой в противоположные
стороны
1
F21
F12
2
F12 F21
Замечание
Силы F21 и F12 приложены к разным телам и не
образуют уравновешенной системы сил
1.3.
АКСИОМЫ СТАТИКИ
1.1.
СТАТИКИ
1.2. АКСИОМЫ
ОСНОВНЫЕ
ПОНЯТИЯ
И МОДЕЛИ
13
14. Аксиома 5. Аксиома отвердевания
Равновесие деформированного тела не нарушится,если его заменить абсолютно твердым
Замечание
Эта аксиома дает необходимое, но не достаточное
условие равновесия деформируемых тел
Пример. Равновесие гибкой нити
F1
F1
1.3.
АКСИОМЫ
1.1.
СТАТИКИ
1.2. АКСИОМЫ
ОСНОВНЫЕСТАТИКИ
ПОНЯТИЯ
И МОДЕЛИ
• Необходимо, чтобы силы
были равны по величине и
противоположно направлены
• Эти силы должны быть
растягивающими
14
15. 1.1.6. Связи
• Механическая система называется свободной,если ее перемещения (положения и/или скорости)
ничем не ограничены
• Механическая система, перемещения (положения
и/или скорости) которой ограничены называется
несвободной
• Ограничения, налагаемые на положения и/или
скорости механической системы, называются
связями
1.3.
АКСИОМЫ
1.1.
СТАТИКИ
1.2. АКСИОМЫ
ОСНОВНЫЕСТАТИКИ
ПОНЯТИЯ
И МОДЕЛИ
15
16. Аксиома 6. Аксиома связей
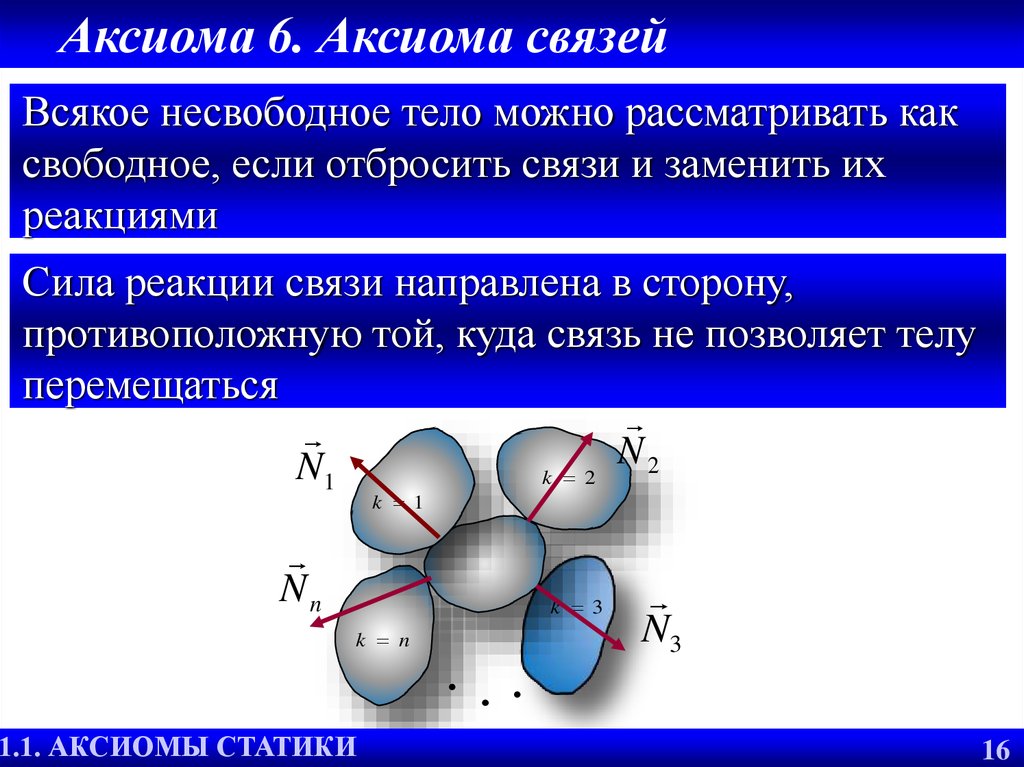
Всякое несвободное тело можно рассматривать каксвободное, если отбросить связи и заменить их
реакциями
Сила реакции связи направлена в сторону,
противоположную той, куда связь не позволяет телу
перемещаться
N1
k 2
N2
k 1
Nn
k 3
k n
...
1.1.
СТАТИКИ
1.4.
СВЯЗИ И РЕАКЦИИ
СВЯЗЕЙ
1.2. АКСИОМЫ
ОСНОВНЫЕ
ПОНЯТИЯ
И МОДЕЛИ
N3
16
17. 1.1.7. Типы связей
• Идеальная нить• Невесомый стержень
• Стержневая опора
• Подвижная шарнирная опора
• Неподвижная шарнирная опора
• Жесткая заделка
• Подпятник
1.4.
СВЯЗИ И РЕАКЦИИ
СВЯЗЕЙ
1.1.
СТАТИКИ
1.2. АКСИОМЫ
ОСНОВНЫЕ
ПОНЯТИЯ
И МОДЕЛИ
17
18. I. Статика
I.2. Система сходящихся сил18
19. 1.2. Система сходящихся сил
• Система сходящихся сил (ССС)• Теорема о равнодействующей ССС
• Условия равновесия произвольной ССС
• Геометрическая интерпретация условий равновесия
• Уравнения равновесия произвольной ССС
• Статически определимые и статически неопределимые
системы
1.4.
СВЯЗИ И РЕАКЦИИ
СВЯЗЕЙ
I. СТАТИКА
1.2.
ОСНОВНЫЕ
ПОНЯТИЯ
И МОДЕЛИ
19
20. 1.2.1. Определение
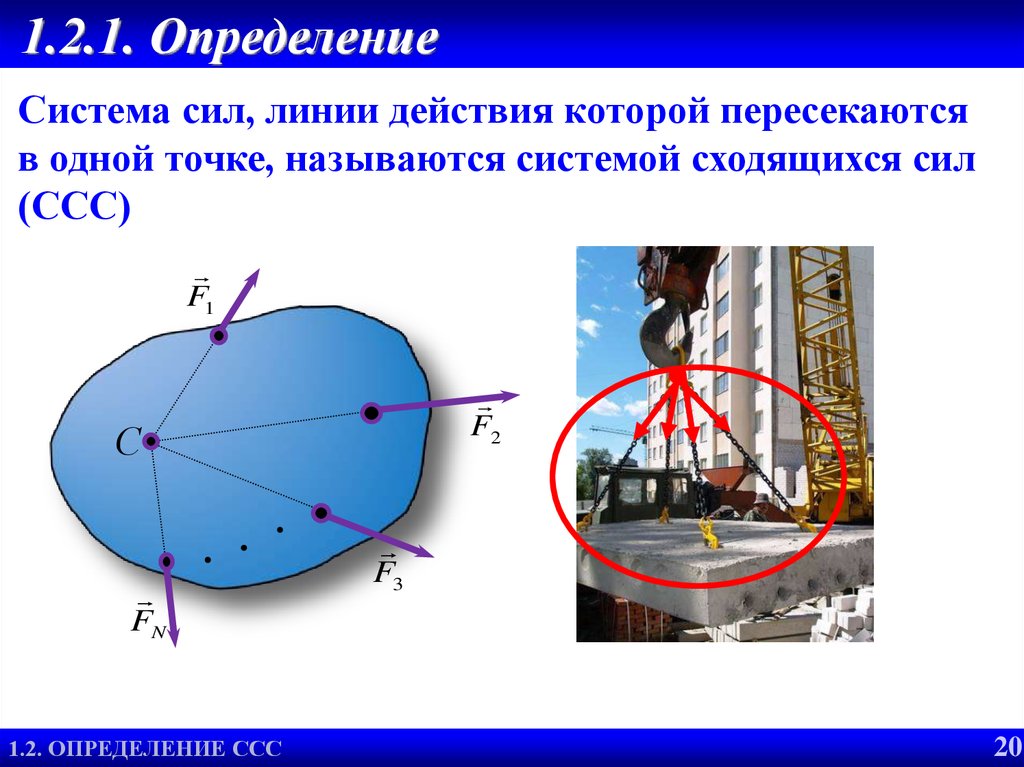
Система сил, линии действия которой пересекаютсяв одной точке, называются системой сходящихся сил
(ССС)
F1
F2
С
FN
2.1. ОПРЕДЕЛЕНИЕ ССС
1.2.
F3
20
21. 1.2.2. Теорема о равнодействующей CCC
Система сходящихся сил имеет равнодействующую,равную геометрической сумме этих сил и проходящую
F1
через точку пересечения их линий действия
F1
R12 F
2
Доказательство
• Перенесем силы в точку
пересечения линий действия
• Складывая затем силы попарно
по правилу параллелограмма
R12 F1 F2 ,
FN
R 123 R 12 F3 F1 F2 F3 ,
……..
N
R Fi
i 1
1.2. УСЛОВИЯ
СИСТЕМАРАВНОВЕСИЯ
СХОДЯЩИХСЯ СИЛ
2.2.
С
R123
F3
R
Теорема доказана
21
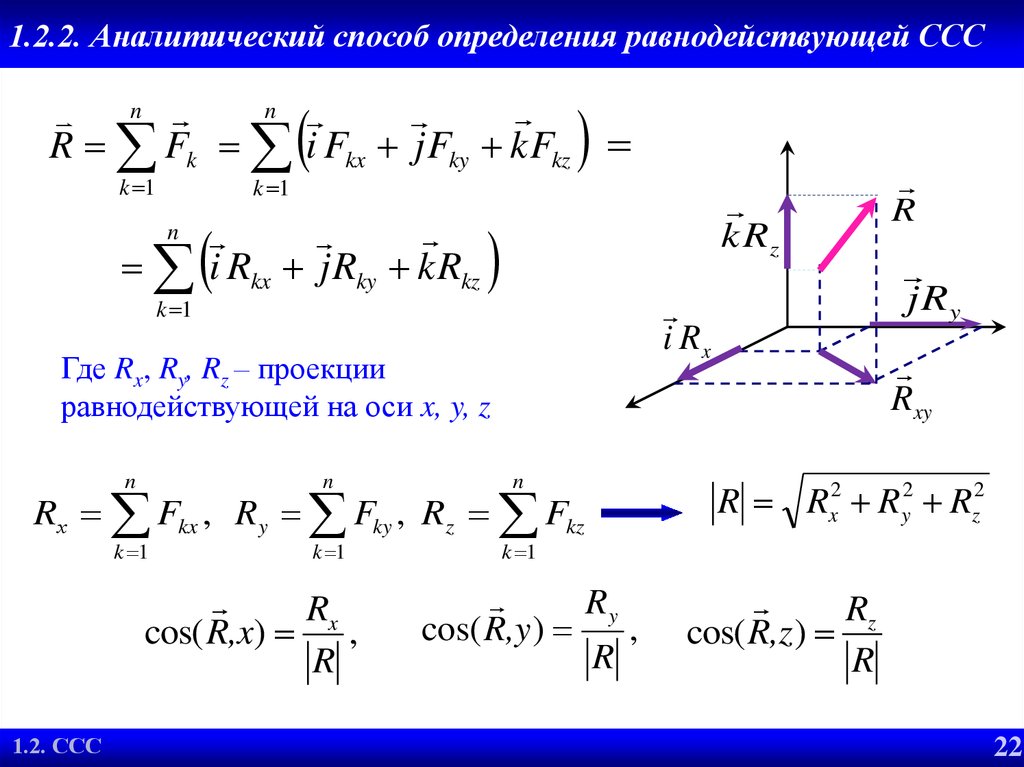
22. 1.2.2. Аналитический способ определения равнодействующей ССС
nn
R Fk i Fkx j Fky k Fkz
k 1
k 1
n
k 1
i Rkx j Rky k Rkz
k Rz
i Rx
Где Rx, Ry, Rz – проекции
равнодействующей на оси x, y, z
n
n
n
k 1
k 1
k 1
Rх Fkx , R y Fky , Rz Fkz
Rx
cos( R,x) ,
R
1.2. УСЛОВИЯ
ССС
2.2.
РАВНОВЕСИЯ
Ry
cos( R,y )
,
R
R
j Ry
Rxy
R Rx2 Ry2 Rz2
Rz
cos( R,z )
R
22
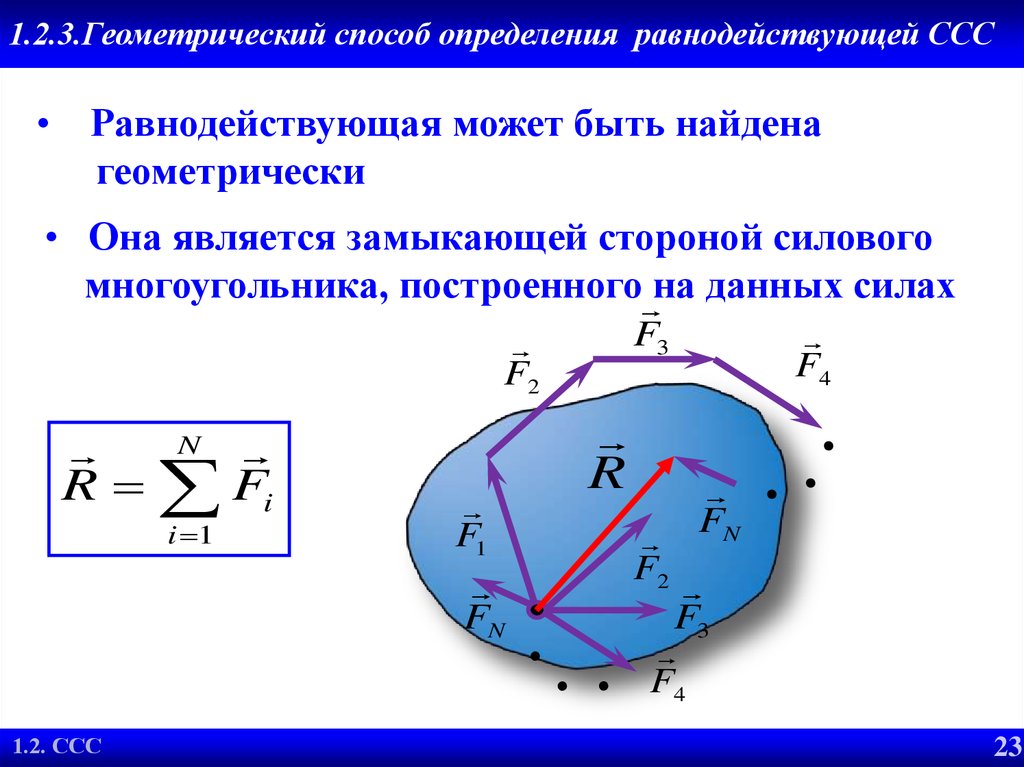
23. 1.2.3.Геометрический способ определения равнодействующей ССС
• Равнодействующая может быть найденагеометрически
• Она является замыкающей стороной силового
многоугольника, построенного на данных силах
N
R Fi
i 1
1.2. УСЛОВИЯ
ССС
2.2.
РАВНОВЕСИЯ
F1
FN
F4
F3
F2
R
F2
FN
F3
F4
23
24. 1.2.4. Условия равновесия тела под действием ССС
Действие на тело произвольной ССС эквивалентнодействию одной силы, равнодействующей
N
{F1 , F2 , , F1} ~ R Fi
i 1
Но если тело находится в равновесии под действием
одной силы, то эта сила равна нулю
N
R Fi 0
i 1
Геометрически это условие означает
замкнутость
силового многоугольника сил {F1 , F2 , , F1}
1.2. УСЛОВИЯ
ССС
2.2.
РАВНОВЕСИЯ
24
25. 1.2.5. Уравнения равновесия CCC
Тело под действием ССС находится в равновесии, еслиR i Rx j Ry k Rz 0
Это векторное уравнение содержит сумму трех взаимно
перпендикулярных векторов. Поэтому оно удовлетворяется
,
только, если нулю равен каждый
из слагаемых
n
n
n
i 1
i 1
i 1
Rx Fix 0, R y Fiy 0, Rz Fiz 0
Если на тело действует плоская ССС, скажем, в плоскости
xy, то данная система уравнений сводится к следующей
n
n
i 1
i 1
Rx Fix 0, R y Fiy 0
1.2. УСЛОВИЯ
ССС
2.2.
2.3.
УРАВНЕНИЯ
РАВНОВЕСИЯ
РАВНОВЕСИЯ
25
26.
F11.2.6. Теорема о трех силах
Если твердое тело находится в равновесии под
действием трех сил, причем линии действия двух
из них пересекаются, то эти силы образуют ССС
Доказательство
Пусть линии действия двух первых
сил пересекаются
F1
R12
( F 1,F 2 ,F 3 ) ~ ( R12 ,F 3 )
Но согласно А1 эти силы
должны быть равны по
величине и противоположно
направлены
С
F2
F3
Линия действия силы проходит через С. Теорема доказана
1.2. УСЛОВИЯ
ССС
2.4.
ТЕОРЕМА РАВНОВЕСИЯ
О ТРЕХ СИЛАХ
2.2.
26
27. 1.2.7. Алгоритм решения задач статики
1. Установить, исследование равновесия какого тела(точки, системы тел) следует рассмотреть
2. Освободить тело от связей и изобразить действующие
на него активные силы и силы реакций отброшенных
связей
3. Установить, какая система сил действует на тело, и
сформулировать условия равновесия этой системы
4. Составить уравнения равновесия
5. Решить уравнения равновесия и определить искомые
неизвестные
Замечание
Если число неизвестных не превышает числа уравнений
равновесия, то система называется статически определенной,
в противном случае – статически неопределенной
1.2. РЕШЕНИЯ
ССС
2.5.
ЗАДАЧ СТАТИКИ
2.2.
УСЛОВИЯ
РАВНОВЕСИЯ
27
28. I. Статика
I.3. Момент силы28
29. 1.3. Момент силы
• Момент силы относительно точки• Момент силы относительно оси
• Теорема Вариньона для ССС
• Теорема о связи момента силы относительно
точки и относительно оси
• Алгебраическое понятие момента силы для ПСС
• Плечо силы
1.4.
СВЯЗИ
И РЕАКЦИИ
СВЯЗЕЙ
I.
СТАТИКА
1.2.
ОСНОВНЫЕ
ПОНЯТИЯ
И МОДЕЛИ
29
30. 1.3.1. Момент силы относительно точки
FMo
O
h
r
b
A
Моментом силы F относительно
точки
О называется вектор
, равный
M
o (F )
векторному произведению
радиус
вектора точкиrприложения
силы
и
силы:
M (F ) r F
o
Момент силы
перпендикулярно плоскости
направлен
векторов r и F и в ту сторону, откуда вращение тела
происходит против часовой стрелки
| M o ( F ) | | r || F | sin b
h | r | sin b
| M o ( F ) | Fh
Плечо силы h – это кратчайшее расстояние от точки, относительно которой вычисляется момент до линии ее действия
1.3. УСЛОВИЯ
МОМЕНТ СИЛЫ
2.2.
РАВНОВЕСИЯ
22
31. 1.3.1. Момент силы относительно точки
M o (F ) r Fi j k
M O ( F ) x y z ( yFz zFy )i ( zFx xFz ) j ( xFy yFx )k
Fx Fy Fz
где x, y, z – координаты точки приложения силы, а Fx , Fy , Fz–
проекции силы на оси координат
M o ( F ) i M ox j M oy k M oz
M Ox ( F ) yFz zFy , M Oy zFx xFz , M Oz ( F ) xFy yFx
1.4.
МОМЕНТ СИЛЫ
1.3. УСЛОВИЯ
МОМЕНТ
СИЛЫ
2.2.
РАВНОВЕСИЯ
31
18
32. 1.3.2. Момент силы на плоскости
i j kM o (F ) r F
Y
F
y
Fx
O
Fy
r
A
X
x
M O (F )
Z
M O ( F ) x y 0 ( xFy yFx )k
Fx Fy 0
F OXY
Fhk
M O ( F ) || k
• Вектор момента силы имеет одну
составляющую и направлен перпендикулярно плоскости, в которой лежит
сила и центр
mO ( F ) M O ( F ) F h
• Алгебраический момент силы mO (F ) имеет знак плюс, если
под действием силы тело поворачивается против часовой
стрелки, и минус – в противном случае
1.3. УСЛОВИЯ
МОМЕНТ
СИЛЫ
2.2.
РАВНОВЕСИЯ
1.4.
МОМЕНТ СИЛЫ
32
20
33. 1.3.3. Теорема Вариньона
Момент равнодействующей системы сходящихся силотносительно произвольной точки O равен векторной
сумме моментов слагаемых сил относительно той же
точки
Доказательство
Векторное произведение удовлетворяет закону дистрибутивности
r ( F1 F2 Fn ) r F1 r F2 r Fn
R F1 F2 Fn
M O (R) rО ( F1 F2 Fn ) M O ( Fk )
Теорема доказана
1.3. УСЛОВИЯ
МОМЕНТ
СИЛЫ
2.2.
РАВНОВЕСИЯ
1.4.
МОМЕНТ СИЛЫ
33
34. 1.3.4. Момент силы относительно оси
F1.3.4. Момент силы относительно оси
• Тело под действием данной
силы будет вращаться
относительно оси Oz
z
F
( xy )
O
h F xy
Fz
A
• Это вращение характеризуется скалярной величиной,
называемой моментом силы
относительно оси Oz
• За вращательное движение
отвечает сила
Моментом силы F относительно оси OZ называется скалярная
величина, равная алгебраическому моменту проекции этой
силы на плоскость, перпендикулярную оси относительно точки
пересечения данной оси с этой плоскостью
M z ( F ) M z ( Fxy ) Fxy h
1.3. УСЛОВИЯ
МОМЕНТ СИЛЫ
2.2.
РАВНОВЕСИЯ
34
35. 1.3.5. Теорема о связи момент силы относительно точки и оси
ZA
O
Y
y
Fy
x
X
Чтобы найти момент силы F относительно
оси Oz, воспользуемся теоремой Вариньона
F
Fx
Fxy
M z ( F ) M z ( Fxy ) xFy yFy M Oz (F )
Аналогично
M x ( F ) M Ox ( F ) yFz zFy , M y ( F ) M Oy ( F ) zFx xFz
Теорема
Моменты сил относительно осей в системе координат
ОXYZ равны проекциям момента силы относительно
начала координат О
1.3. УСЛОВИЯ
МОМЕНТ
СИЛЫ
2.2.
РАВНОВЕСИЯ
1.4.
МОМЕНТ СИЛЫ
35
24
36. I. Статика
I.4. Система параллельных сил (СПС)36
37. 1.4. Система параллельных сил
Теорема о сложении двух параллельных сил,
направленных в одну сторону
Разложение данной системы на две ей параллельные
Центр СПС
Центр тяжести
Методы определения центров тяжести
• Распределенные силы
1.4.
СВЯЗИ
И РЕАКЦИИ
СВЯЗЕЙ
I.
СТАТИКА
1.2.
ОСНОВНЫЕ
ПОНЯТИЯ
И МОДЕЛИ
37
38.
1.4.1. Теорема о равнодействующей двух силСистема двух параллельных сил,
направленных в одну сторону, имеет
равнодействующую, равную по модулю
сумме их модулей, параллельна им и
направлена в ту же сторону.
Линия действия равнодействующей делит
отрезок между точками приложения данных
сил обратно пропорционально их величине
2.1.
ССС В ОДНУ СТОРОНУ
1.4. ОПРЕДЕЛЕНИЕ
СПС, НАПРАВЛЕННЫЕ
38
39. Равнодействующая СПС
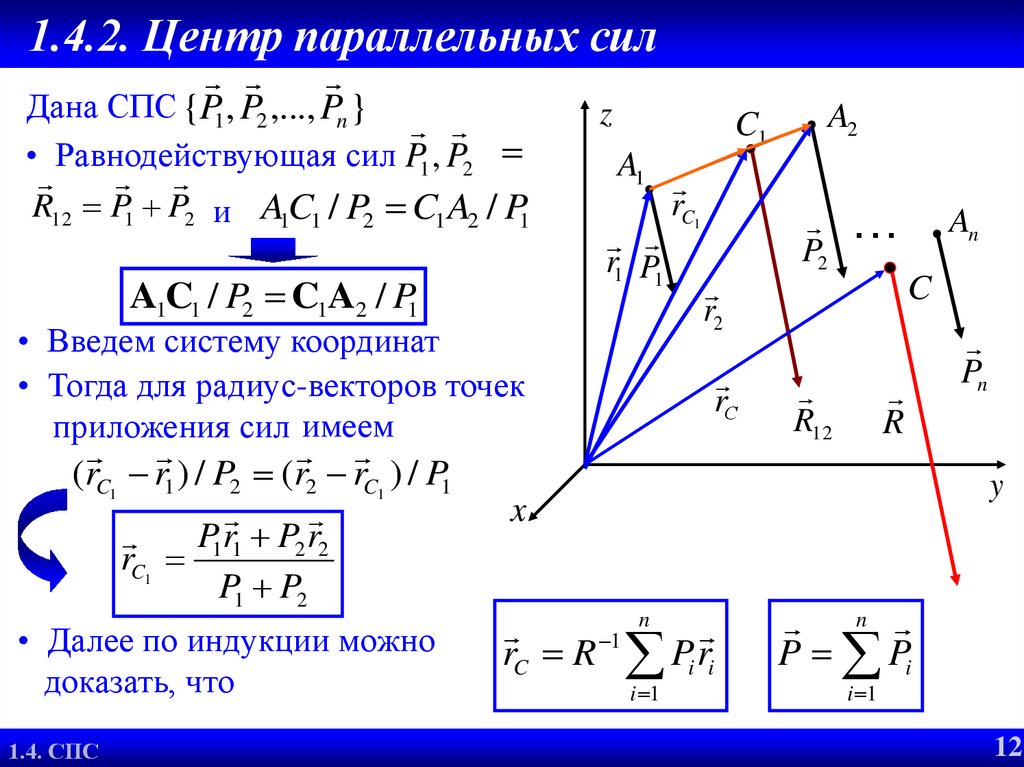
1.4.2.Центр параллельных
Равнодействующая
СПСсил
Дана СПС {P1 , P2 ,..., Pn }
• Равнодействующая сил P1 , P2
R12 P1 P2 и A1C1 / P2 C1 A2 / P1
A1C1 / P2 C1A2 / P1
z
A1
r1 P1
• Введем систему координат
• Тогда для радиус-векторов точек
приложения сил имеем
(rC1 r1 ) / P2 (r2 rC1 ) / P1
P1r1 P2 r2
rC1
P1 P2
• Далее по индукции можно
доказать, что
A2
C1
rC1
r2
rС
P2
...
An
C
R
R12
y
x
n
1
rC R Pi ri
2.1.
ССС
3.3. ОПРЕДЕЛЕНИЕ
1.4.
СПС
ЦЕНТР СИСТЕМЫ
ПАРАЛЛЕЛЬНЫХ СИЛ
Pn
i 1
n
P Pi
i 1
12
11
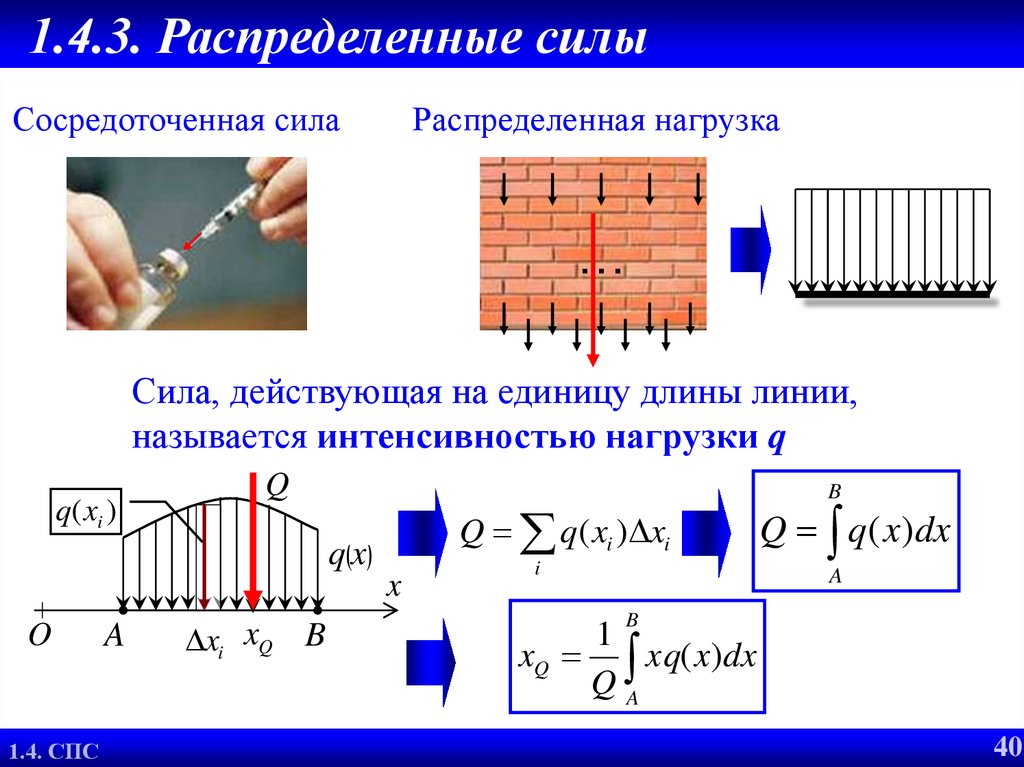
40. Распределенные силы
1.4.3.Распределенные
Распределенные
силы силы
Сосредоточенная сила
Распределенная нагрузка
…
Сила, действующая на единицу длины линии,
называется интенсивностью нагрузки q
q( xi )
Q
Q q( xi ) xi
q x
x
O
A
xi xQ B
2.1.
ССС
3.3. ОПРЕДЕЛЕНИЕ
1.4.
СПС
ЦЕНТР СИСТЕМЫ
ПАРАЛЛЕЛЬНЫХ СИЛ
i
B
Q q( x)dx
A
B
1
xQ xq( x)dx
QA
40
13
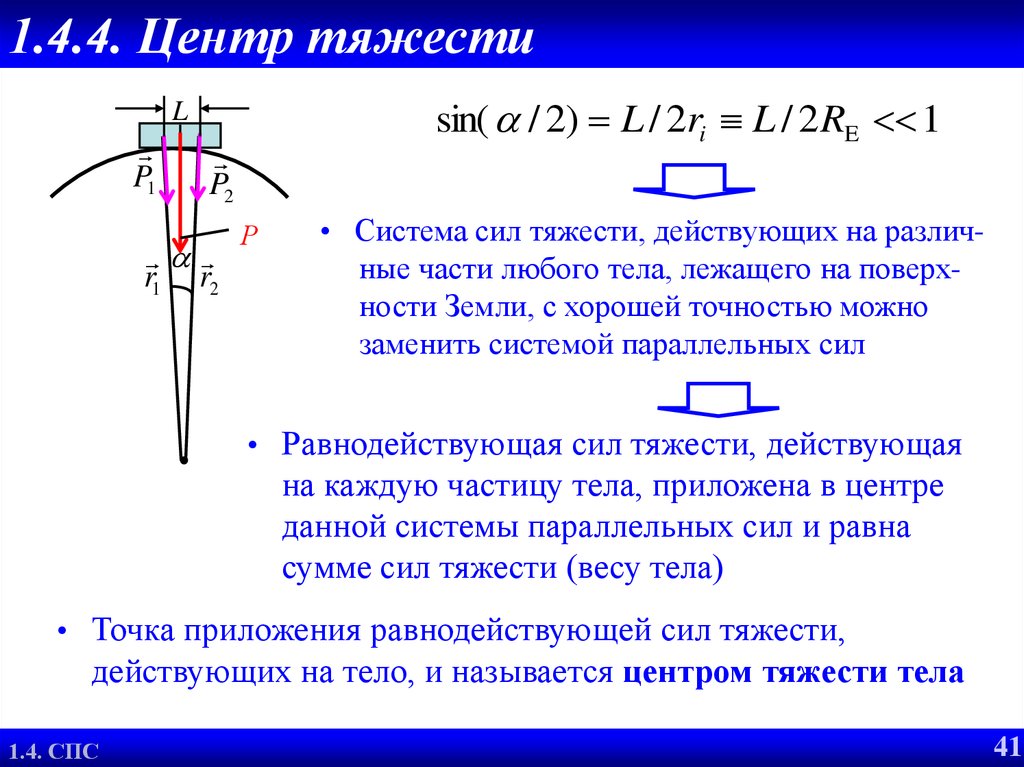
41. 1.4.4. Центр тяжести
sin( / 2) L / 2ri L / 2RE 1L
P1
P2
r1 r2
• Система сил тяжести, действующих на различные части любого тела, лежащего на поверхности Земли, с хорошей точностью можно
заменить системой параллельных сил
Р
• Равнодействующая сил тяжести, действующая
на каждую частицу тела, приложена в центре
данной системы параллельных сил и равна
сумме сил тяжести (весу тела)
• Точка приложения равнодействующей сил тяжести,
действующих на тело, и называется центром тяжести тела
2.1.
ССС
1.4. ОПРЕДЕЛЕНИЕ
СПС
41
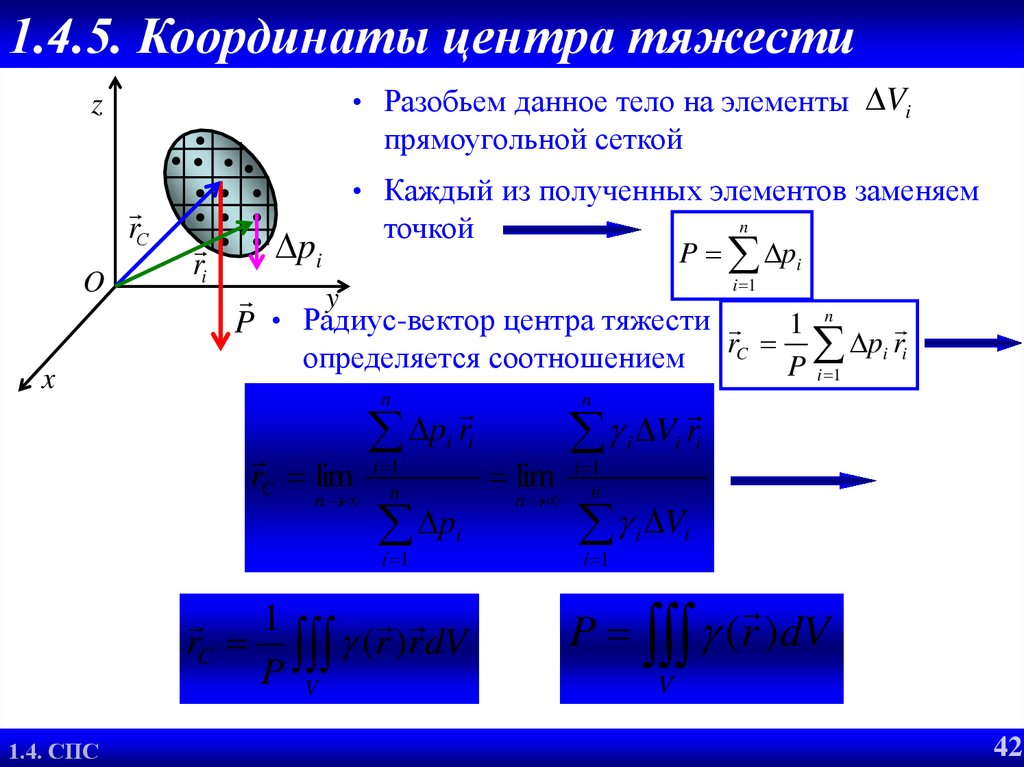
42. 1.4.5. Координаты центра тяжести
• Разобьем данное тело на элементы Viz
прямоугольной сеткой
rС
O
x
• Каждый из полученных элементов заменяем
ri
p i
точкой
n
P pi
i 1
y
P • Радиус-вектор центра тяжести 1 n
rC pi ri
определяется соотношением
P i 1
pi ri
n
rC lim
i 1
n
n
p
i 1
i
1
rC (r )r dV
P V
2.1.
ССС
1.4. ОПРЕДЕЛЕНИЕ
СПС
i Vi ri
n
lim
i 1
n
n
V
i 1
i
i
P (r )dV
V
42
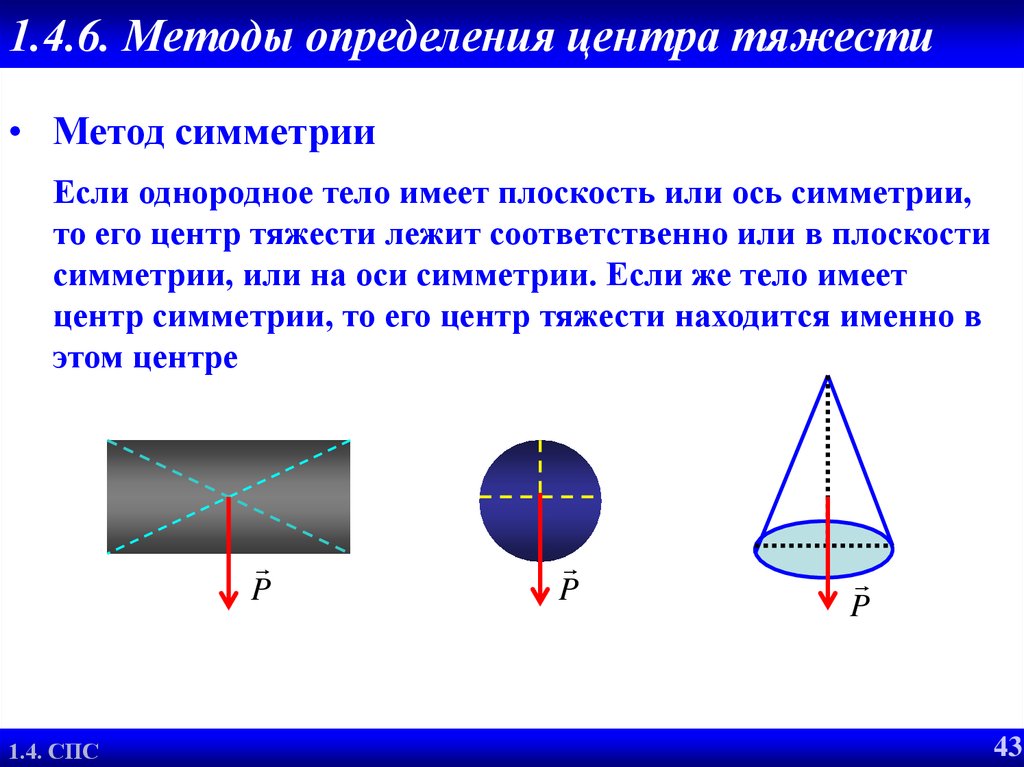
43. 1.4.6. Методы определения центра тяжести
• Метод симметрииЕсли однородное тело имеет плоскость или ось симметрии,
то его центр тяжести лежит соответственно или в плоскости
симметрии, или на оси симметрии. Если же тело имеет
центр симметрии, то его центр тяжести находится именно в
этом центре
P
2.1.
ССС
1.4. ОПРЕДЕЛЕНИЕ
СПС
P
P
43
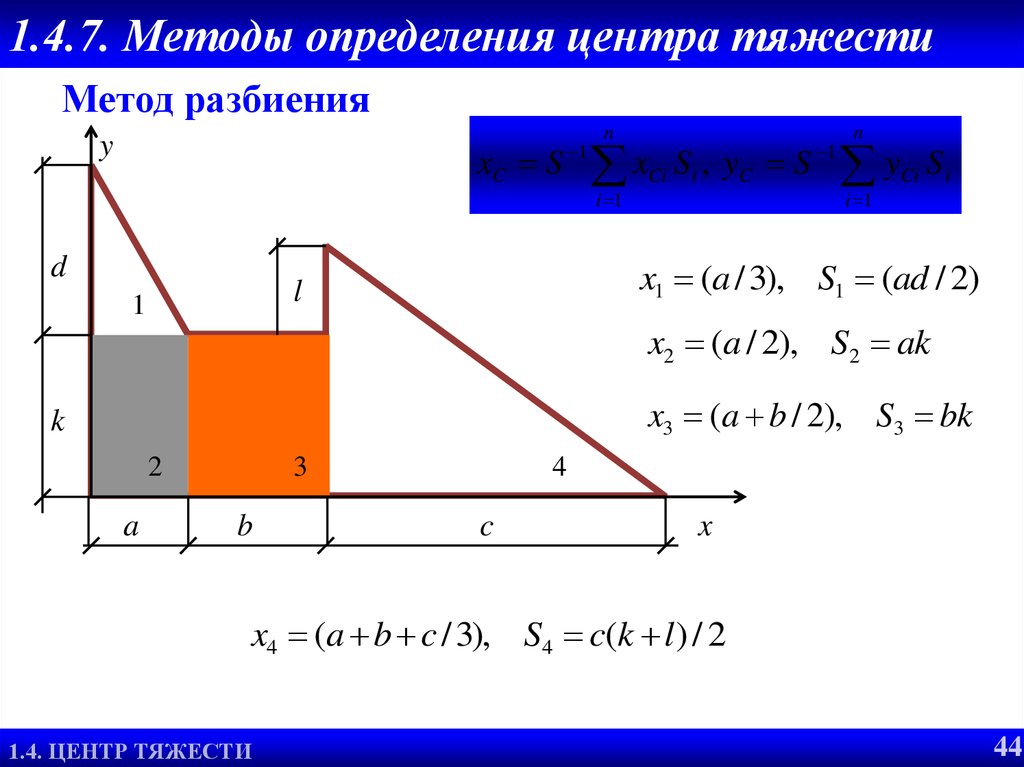
44. 1.4.7. Методы определения центра тяжести
Метод разбиенияn
n
i 1
i 1
xC S 1 xCi Si , yC S 1 yCi S i
y
d
x1 (a / 3), S1 (ad / 2)
l
1
x2 (a / 2), S2 ak
x3 (a b / 2), S3 bk
k
2
a
3
b
4
c
x
x4 (a b c / 3), S4 c(k l ) / 2
2.1.
ССС
1.4. ОПРЕДЕЛЕНИЕ
ЦЕНТР ТЯЖЕСТИ
44
45. 1.4.8. Методы определения центра тяжести
Метод дополнений (отрицательных весов)• Пусть тело, вес которого P, имеет полость заданного объема V. Если бы тело
не имело полости, то его вес был бы равен P’ = P+PV, где PV – вес объема V.
• Радиус-вектор тела без полости тогда равен
'
rc rC P rCV PV / P'
y
для тела с полостью
'
rC rС P' rCV PV / P
Задача 8
2
1
a/2
x
xC
x1S1 x2 S 2 a(16 )
S1 S 2
4(8 )
yC
y1S1 y2 S 2 a
S1 S 2
4
a
2.1.
ССС
1.4. ОПРЕДЕЛЕНИЕ
СПС
45
46. I. Статика
I.5. Теория пар сил46
47. 1.5. Теория пар сил
• Теорема о равнодействующей двухпараллельных сил, направленных
в противоположные стороны
• Пара сил
• Момент пары сил
• Момент пары как вектор
• Теорема об эквивалентных парах
• Теорема о сложении пар
• Условия равновесия пар
• Жесткая заделка
1.4.
И РЕАКЦИИ
СВЯЗЕЙ
1.5.СВЯЗИ
СТАТИКА
1.2.
ОСНОВНЫЕ
ПОНЯТИЯ
И МОДЕЛИ
47
48.
1.5.1. Теорема о равнодействующей двух силСистема двух не равных по модулю сил, линии
действия которых параллельны, но силы
направлены противоположно, имеет
равнодействующую, которая равна по модулю
разности модулей этих сил, им параллельна и
направлена в сторону большей силы.
Линия действия равнодействующей проходит через
точку, которая лежит на продолжении отрезка АВ
и делит этот отрезок внешним образом на части,
обратно пропорциональные силам.
2.1.
ССС
1.5. ОПРЕДЕЛЕНИЕ
ТЕОРИЯ ПАР СИЛ
48
49.
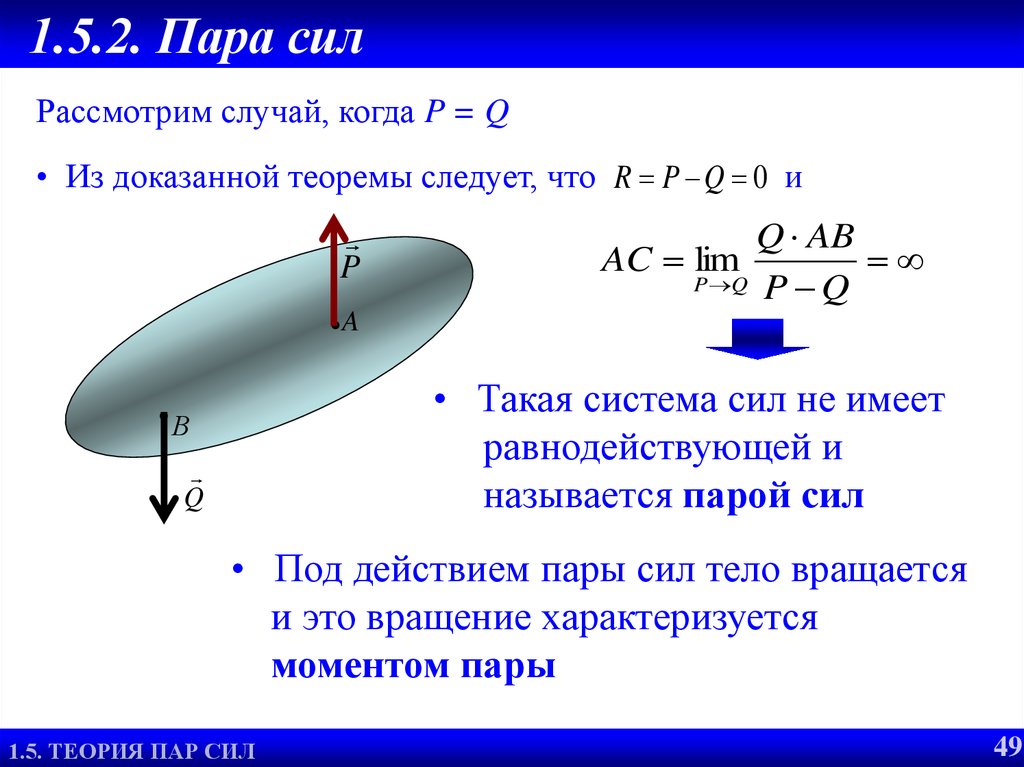
1.5.2. Пара силРассмотрим случай, когда P = Q
• Из доказанной теоремы следует, что R P Q 0 и
P
Q AB
AC lim
P Q P Q
A
• Такая система сил не имеет
равнодействующей и
называется парой сил
В
Q
• Под действием пары сил тело вращается
и это вращение характеризуется
моментом пары
2.1.
ССС
ПАРА
СИЛ ПАР СИЛ
1.5. ОПРЕДЕЛЕНИЕ
ТЕОРИЯ
49
50.
1.5.3. Момент парыПусть дана пара сил ( F , F1 )
M
• Плоскость, проходящая через
F1
линии действия сил, называется
А
плоскостью действия пары
B
• Расстояние между линиями действия
F
сил называется плечом пары
Моментом пары сил называется вектор , модуль которого равен
произведению модуля одной из сил пары на плечо пары: M=Fd.
Направлен этот вектор перпендикулярно плоскости действия пары
в сторону, откуда вращение пары видно происходящим против
часовой стрелки.
Для пар сил, расположенных в одной плоскости можно
использовать понятие алгебраического момента пары: M = ±Fd.
Знак "плюс" берется, если пара стремится повернуть тело против
хода часовой стрелки, "минус" – по ходу.
2.1.
ССС
ПАРА
СИЛ ПАР СИЛ
1.5. ОПРЕДЕЛЕНИЕ
ТЕОРИЯ
50
51.
1.5.4. Момент пары как векторz
F1
А
F2
O
x
B
y
Момент пары сил ( F , F1 ) равен
M M A ( F2 ) M B ( F1 ) AB F2
• Введем систему координат Оxyz
M AB F2 (OB OA) F2
OB F2 OA F2 OB F2 OA F1
M M O ( F1 ) M O ( F2 )
Сумма моментов сил пары относительно любой точки О равна
моменту пары этих сил. Поскольку момент пары сил перпенди-
кулярен плоскости пары, а его модуль равен M AB F1 sin( AB, F1 ),
то момент пары не зависит от точек приложения сил пары.
Он определяется лишь плечом пары.
2.1.
ССС
ПАРА
СИЛ ПАР СИЛ
1.5. ОПРЕДЕЛЕНИЕ
ТЕОРИЯ
52
52. Доказательство
1.5.5.Теорема
об
эквивалентности
пар
сил
Доказательство
Все пары сил, имеющие один и тот же момент,
эквивалентны.
Доказательство Дана пара сил ( F , F ) с моментом m = Fh
Q
A
d
f
F
C
h
Q
• Разложим каждую из них по двум
{ f , Q }
направлениям на силы { f , Q},
( F , F ) ~ ( f , Q, f , Q ) но ( f , f ) ~ 0
F
B
f
( F , F ) ~ (Q, Q )
• Момент пары (Q, Q ) равен m Qd
Так как ABC ~ FQf то d hF Q
m Qd (Qh ) F / Q Fh m
Теорема доказана для пар, лежащих в одной плоскости
2.1.
ССС
ТЕОРЕМА
ОБ
ЭКВИВАЛЕНТНОСТИ
ПАР СИЛ
1.5. ОПРЕДЕЛЕНИЕ
ТЕОРИЯ
ПАР
СИЛ
52
53. Доказательство
1.5.6.Теорема
об
сложении
пар
сил
Доказательство
M1 , M 2 ,..., M N
Действие на тело системы пар с моментами
Эквивалентно действию одной пары с моментом
Q1
R1
A
F1
B
R1
N
M Mk
Q1
k 1
• Докажем сначала теорему для двух пар сил
• Из теоремы об эквивалентности пар следует, что
F1
для доказательства достаточно рассмотреть две
пары, точки приложения сил которых A и B
совпадают
• Рассмотри две пары сил ( F1 , F1 ) и (Q1 , Q1 )
• Действие рассматриваемых
двух пар эквивалентно
действию одной пары ( R1 , R1 ) с моментом
M AB R1 AB ( F1 Q1 ) AB F1 AB Q1 M1 M 2
Для N пар можно доказательство получается по индукции.
ТЕОРЕМА
О ПАР
СЛОЖЕНИИ
2.1.
ССС ПАР СИЛ
1.5. ОПРЕДЕЛЕНИЕ
ТЕОРИЯ
СИЛ
53
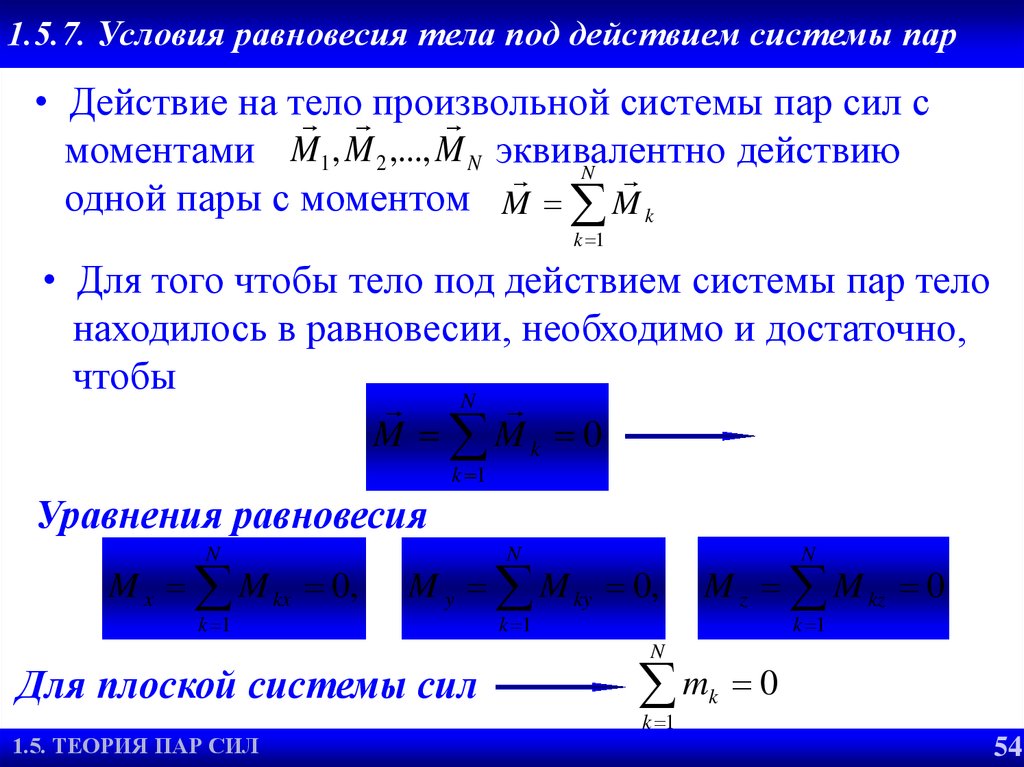
54. 1.5.7. Условия равновесия тела под действием системы пар
• Действие на телосистемы пар сил с
произвольной
моментами M1 , M 2 ,..., M N эквивалентно
действию
N
одной пары с моментом M M k
k 1
• Для того чтобы тело под действием системы пар тело
находилось в равновесии, необходимо и достаточно,
чтобы
N
M Mk 0
k 1
Уравнения равновесия
N
M x M kx 0,
k 1
M y M ky 0,
Для плоской системы сил
1.5. УСЛОВИЯ
ТЕОРИЯ ПАР
СИЛ
2.2.
РАВНОВЕСИЯ
N
k 1
N
M z M kz 0
k 1
N
m
k 1
k
0
54
55. 1.5.8. Жесткая заделка
• Жесткая заделка – это вид связи, полностью запрещающейдвижение тела
• Пример – балка, один конец которой защемлен
• Реакция жёсткой заделки представляет собой совокупность
силы и пары сил, которые образуют плоскую или
пространственную систему сил в зависимости от того,
какими являются активные силы.
Графическое представление
Реакция жесткой заделки
y
YA
А
mA
1.5. РЕШЕНИЯ
ТЕОРИЯ ПАР
СИЛСТАТИКИ
2.5.
ЗАДАЧ
2.2.
УСЛОВИЯ
РАВНОВЕСИЯ
XA
x
55
56. I. Статика
I.6. Основная теорема статики56
57. 1.6. Основная теорема статики
• Теорема о параллельном переносе силы• Главный вектор и главный момент системы
• Основная теорема статики (теорема Пуансо)
• Условия равновесия произвольной системы сил
• Уравнения равновесия
• Три формы уравнений равновесия ПСС
• Приведение пространственной системы сил к
простейшему виду
• Статические инварианты
1.4.
И РЕАКЦИИ
СВЯЗЕЙ
1.6.СВЯЗИ
СТАТИКА
1.2.
ОСНОВНЫЕ
ПОНЯТИЯ
И МОДЕЛИ
57
58. 1.6.1. Лемма о параллельном переносе силы
Действие на твердое тело силы F , приложенной в точкеA, эквивалентно действию силы F ' , равной исходной по
модулю, параллельной ей и приложенной в точке В, и
паре сил с моментом равным моменту данной силы
относительно точки В
F
F'
F'
В
A
Доказательство
• Добавим к силе
F уравновешенную
систему сил {F ' , F '} ~ 0 в точке В
F ~ {F , F ' , F '}
• Но силы F , F ' образуют пару сил с
моментом
M ( F , F ' ) BA F M B ( F )
Теорема доказана
2.1.
ССС СТАТИКИ
1.6. ОПРЕДЕЛЕНИЕ
ОСНОВНАЯ ТЕОРЕМА
58
59.
1.6.2. Главный векторГлавным
*вектором данной системы сил называется
вектор R , равный сумме всех сил системы
* n
R Fi
i 1
Замечание
• Главный вектор определен для любой системы, а равнодействующая в ряде случаев просто не существует
• Главный вектор системы сил не зависит от центра
приведения
2.1.
ССС СТАТИКИ
1.6. ОПРЕДЕЛЕНИЕ
ОСНОВНАЯ ТЕОРЕМА
59
60.
1.6.3. Главный моментГлавным моментом данной системы сил относительно
*
точки А называется вектор M A , равный сумме моментов
всех сил системы относительно той же точки
n
n
*
M A M Ai M A ( Fi )
i 1
i 1
Замечание
• Главный момент
центра
меняется
при смене
приведения
Действительно, M Ai rAK Fi , а M Bi rBK Fi
n
n
**
Fi
M
MAA M A ( Fi ) rAK Fi
rAK
i 1
i 1
n
n
n
К
А
(rAB rBK ) Fi rAB Fi rBK Fi
rВK
rАВ
i 1
i 1
i 1
B
rAB R* M B*
2.1.
ССС СТАТИКИ
1.6. ОПРЕДЕЛЕНИЕ
ОСНОВНАЯ ТЕОРЕМА
60
61. Теорема о равнодействующей двух сил
Теорема1.6.4. Теорема
о равнодействующей
Пуансо (1804 г.) двух сил
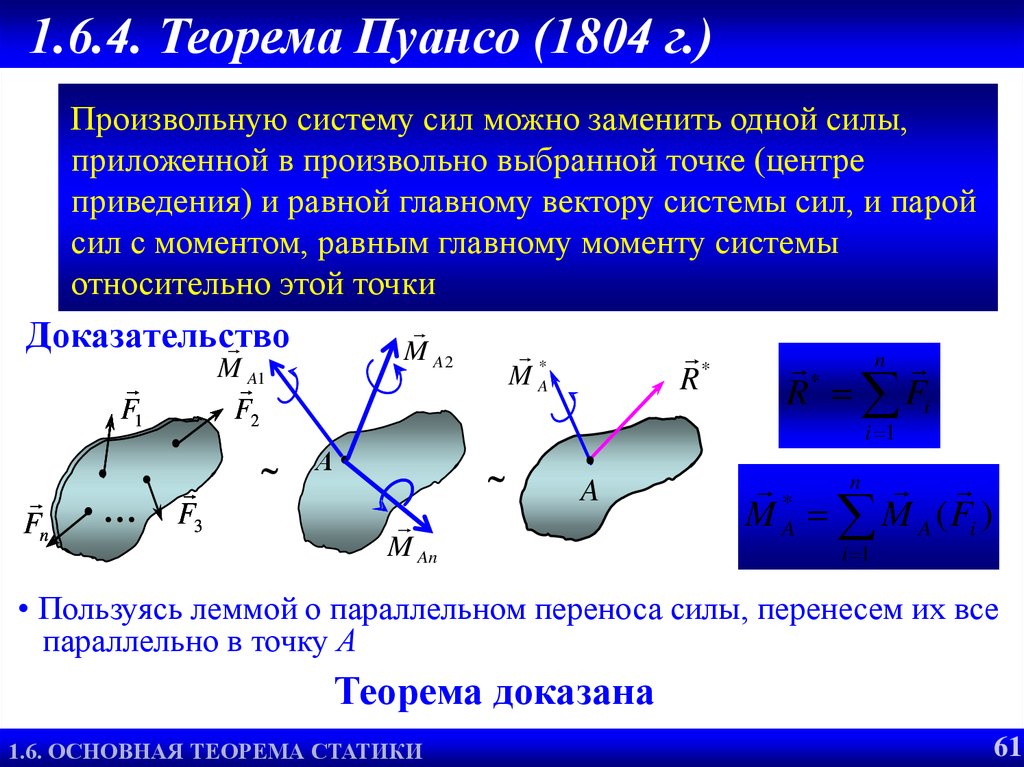
Произвольную систему сил можно заменить одной силы,
приложенной в произвольно выбранной точке (центре
приведения) и равной главному вектору системы сил, и парой
сил с моментом, равным главному моменту системы
относительно этой точки
M A2
Доказательство
M A1
F1
Fn
…
F2
F3
*
R
*
MA
* n
R Fi
i 1
~
А
~
M An
A
n
*
M A M A ( Fi )
i 1
• Пользуясь леммой о параллельном переноса силы, перенесем их все
параллельно в точку А
Теорема доказана
2.1.
ССС СТАТИКИ
3.2. ОПРЕДЕЛЕНИЕ
РАВНОДЕЙСТВУЮЩАЯ
ДВУХ СИЛ
1.6.
ОСНОВНАЯ
ТЕОРЕМА
61
8
62. Равнодействующая СПС
1.6.5.Уравнения равновесия
Равнодействующая
СПС
Пусть дана произвольная система сил {F1, F2 ,..., Fn }. Тело под
действием этой системы
в равновесии, если она
сил находится
эквивалента нулю {F1 , F2 ,..., Fn } ~ 0
Но
{F1, F2 ,..., Fn } ~ {R* , M O* )} ~ 0
n
* n
*
R Fi 0,
M O M Oi 0
i 1
i 1
В координатной форме эти уравнения равновесия имеют вид
n
F
i 1
ix
i 1
F
0,
M x ( Fi ) 0,
n
n
i 1
iy
0,
M y ( Fi ) 0,
n
i 1
2.1.
ССС
3.3. ОПРЕДЕЛЕНИЕ
1.6.
ОСНОВНАЯ
ЦЕНТР СИСТЕМЫ
ТЕОРЕМА
ПАРАЛЛЕЛЬНЫХ
СТАТИКИ
СИЛ
n
F
iz
i 1
0
M z ( Fi ) 0
n
i 1
62
11
63. Равнодействующая СПС
1.6.6.Уравнения равновесия
Равнодействующая
СПС ПСС
Пусть все силы находятся в плоскости Oxy. В этом случае проекция
главного вектора на ось Oz равна нулю, а главный момент направлен
параллельно этой оси. Т.о., имеем три уравнения равновесия.
Основная форма уравнений равновесия ПСС
n
n
n
Fix 0, Fiy 0, M А ( Fi ) 0
i 1
i 1
i 1
Вторая форма уравнений равновесия ПСС (АВ Ox)
n
n
n
M А ( Fi ) 0, M В ( Fi ) 0, Fix 0
i 1
i 1
i 1
Третья форма уравнений равновесия ПСС (точки А, В, С не
должны лежать на одной прямой)
n
n
n
M А ( Fi ) 0, M В ( Fi ) 0, M С ( Fi ) 0
i 1
i 1
2.1.
ССС
3.3. ОПРЕДЕЛЕНИЕ
1.6.
ОСНОВНАЯ
ЦЕНТР СИСТЕМЫ
ТЕОРЕМА
ПАРАЛЛЕЛЬНЫХ
СТАТИКИ
СИЛ
i 1
63
11
64.
1.6.7. Статические инвариантыИнварианты – величины, неизменные при некотором
преобразовании. Статические инварианты – величины,
не зависящие от выбора центра приведения.
• I статический инвариант – главный вектор системы сил
* n
R Fi inv
i 1
• II статический инвариант – скалярное произведение
главного вектора и главного момента системы
* *
M A R inv
* * * *
* * * *
Действительно, M A R M B R (rAB R ) R M B R ,
*
*
поскольку (rAB R ) R
2.1.
ССС СТАТИКИ
1.6. ОПРЕДЕЛЕНИЕ
ОСНОВНАЯ ТЕОРЕМА
64
65.
1.6.8. Частные случаи приведения*
• R 0, M A 0 – уравновешенная система сил
*
*
• R 0, M A 0 – система сил приводится к равнодействую*
щей, проходящей через точку А
*
*
• R 0, M А 0 – система сил приводится к паре с моментом,
равным M А* . Главные моменты относительно всех точек в
* * * *
* * * *
этом случае равны: M A R M B R (rAB R ) R M B R
*
*
поскольку (rAB R ) R
*
*
*
• R 0, M А 0 , но M A R* – в этом случае система сил
* *
приводится к равнодействующей. Действительно, M A R 0
*
MA
F'
А
*
R
F
R
2.1.
ССС СТАТИКИ
1.6. ОПРЕДЕЛЕНИЕ
ОСНОВНАЯ ТЕОРЕМА
65
66.
1.6.8. Частные случаи приведения*
*
*
• R 0, M А 0 , но M A || R * – в этом
* случае система
сил
приводится к приводится к силе R и паре сил ( P1 , P2 ) ,
*
лежащей в плоскости, перпендикулярной к R . Такая
совокупность силы и пары сил называется динамой, а
прямая, вдоль которой направлен главный вектор, – осью
динамы.
*
MА
*
R
А
2.1.
ССС СТАТИКИ
1.6. ОПРЕДЕЛЕНИЕ
ОСНОВНАЯ ТЕОРЕМА
*
R
~
P1
P2
66
67. I. Статика
I.7. Трение67
68. 1.7. Трение
• Законы трения покоя• Законы трения скольжения
• Реакции связей при учете трения
• Угол трения
• Конус трения, заклинивание
• Измерение коэффициента трения
• Трение качения
• Равновесие при наличии трения
1.4.
И РЕАКЦИИ
СВЯЗЕЙ
1.7.СВЯЗИ
СТАТИКА
1.2.
ОСНОВНЫЕ
ПОНЯТИЯ
И МОДЕЛИ
68
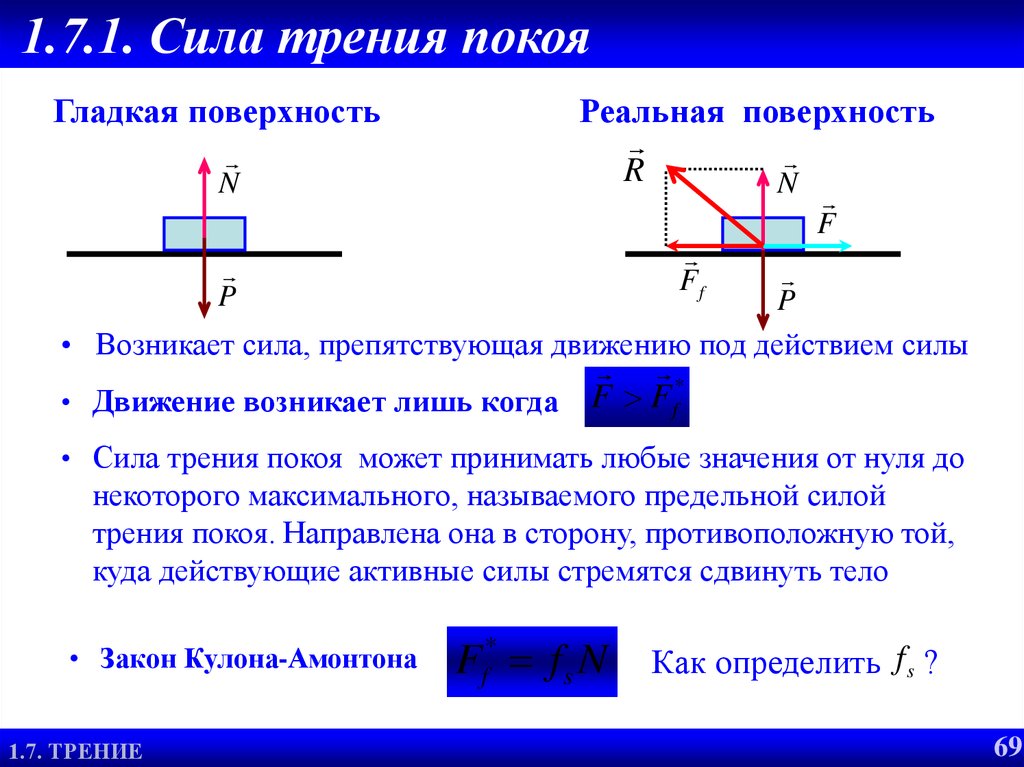
69. 1.7.1. Сила трения покоя
Гладкая поверхностьРеальная поверхность
R
N
N
Ff
P
F
P
• Возникает сила, препятствующая движению под действием силы
*
• Движение возникает лишь когда F Ff
• Сила трения покоя может принимать любые значения от нуля до
некоторого максимального, называемого предельной силой
трения покоя. Направлена она в сторону, противоположную той,
куда действующие активные силы стремятся сдвинуть тело
• Закон Кулона-Амонтона
2.1.
ССС
1.7. ОПРЕДЕЛЕНИЕ
ТРЕНИЕ
F fs N
*
f
Как определить f s ?
69
70. 1.7.2. Определение коэффициента трения
NF
fs F / P
Ff
*
f
P
A
• Коэффициент трения покоя (статический коэффициент трения)
определяется лишь свойствами материалов соприкасающихся тел и не
зависит от площади контакта этих тел
Материал
Медно-свинцовый сплав по стали (без смазки)
Тщательно очищенные металлы по металлу
Стекло по стеклу, очищенные
Дерево по металлу, сухое и очищенное
Кожа по металлу, очищенная сухая
2.1.
ССС
1.7. ОПРЕДЕЛЕНИЕ
ТРЕНИЕ
fs
0.2
100
1
0.2–0.6
0.6
70
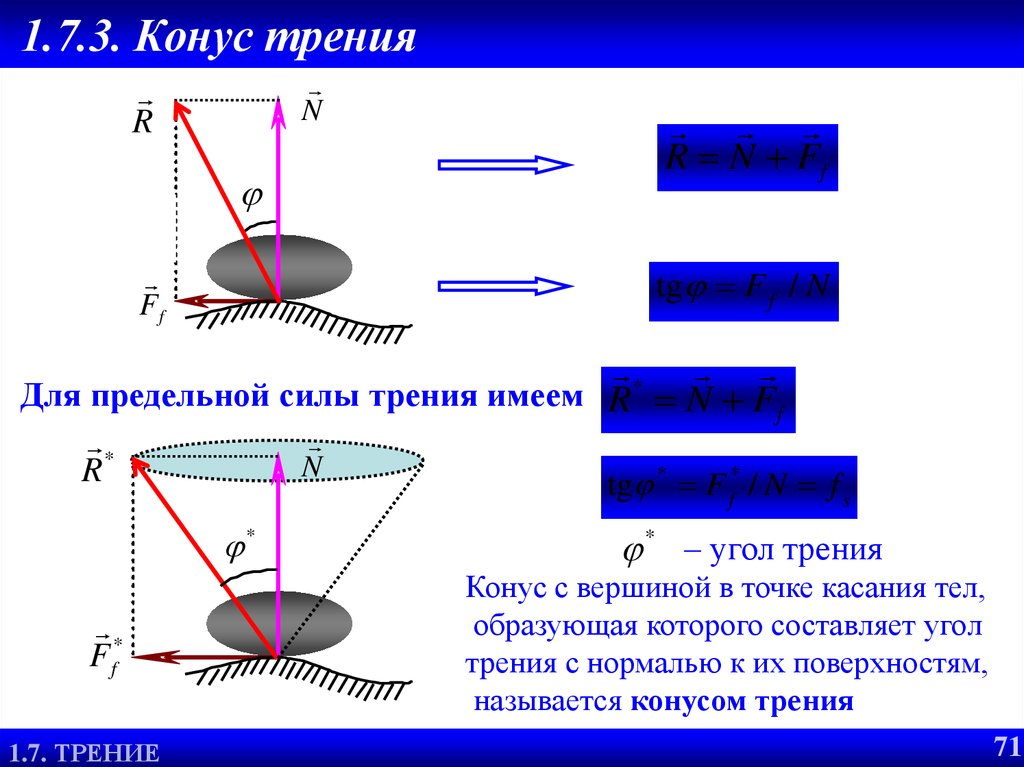
71. 1.7.3. Конус трения
NR
R N Ff
tg F f / N
Ff
*
Для предельной силы трения имеем R N Ff
*
R
N
*
*
Ff
2.1.
ССС
1.7. ОПРЕДЕЛЕНИЕ
ТРЕНИЕ
tg * F f* / N f s
* – угол трения
Конус с вершиной в точке касания тел,
образующая которого составляет угол
трения с нормалью к их поверхностям,
называется конусом трения
71
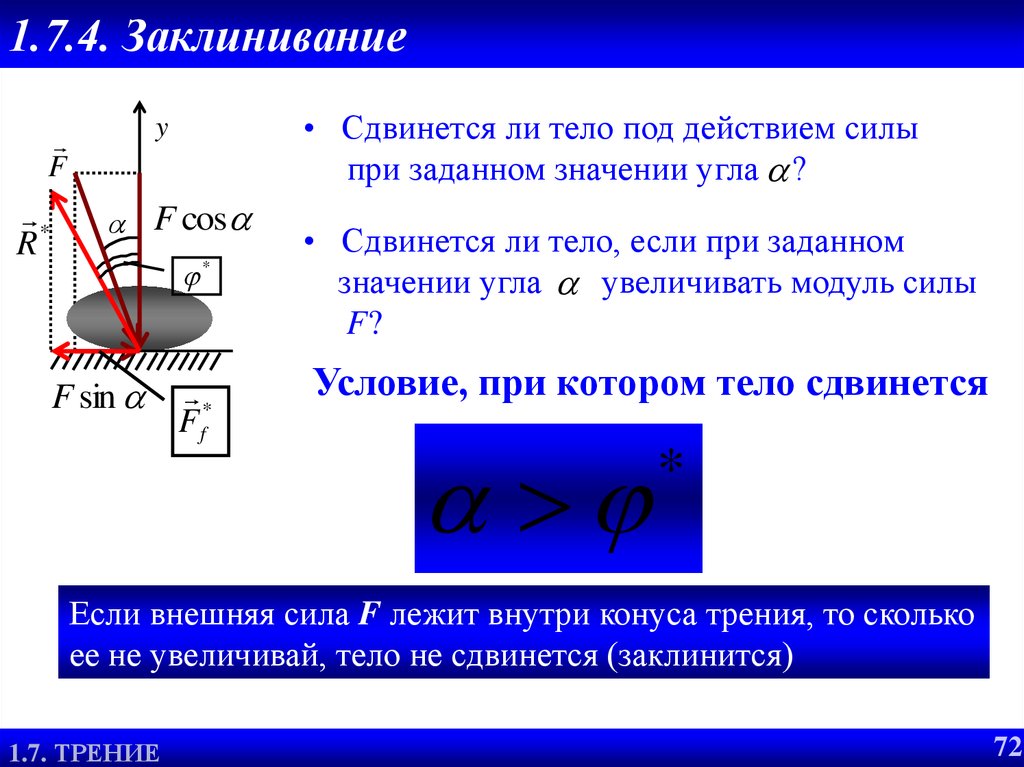
72. 1.7.4. Заклинивание
*R
• Сдвинется ли тело под действием силы
при заданном значении угла ?
y
F
F cos
*
F sin
*
Ff
• Сдвинется ли тело, если при заданном
значении угла увеличивать модуль силы
F?
Условие, при котором тело сдвинется
*
Если внешняя сила F лежит внутри конуса трения, то сколько
ее не увеличивай, тело не сдвинется (заклинится)
2.1.
ССС
1.7. ОПРЕДЕЛЕНИЕ
ТРЕНИЕ
72
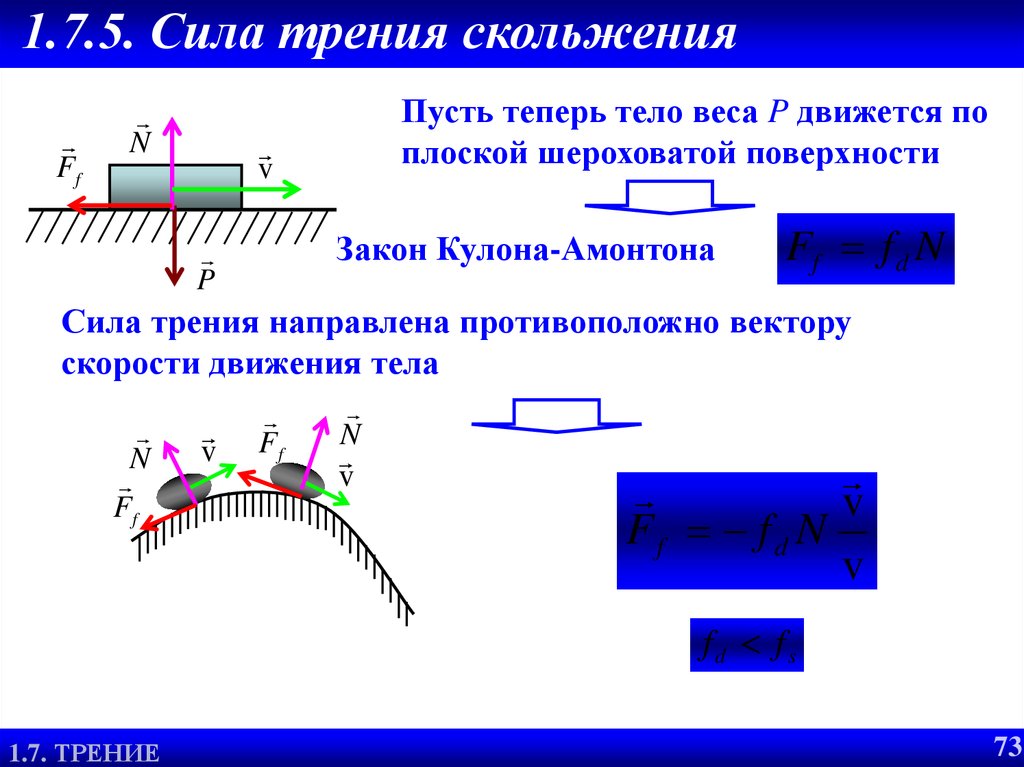
73. 1.7.5. Сила трения скольжения
FfN
Пусть теперь тело веса P движется по
плоской шероховатой поверхности
v
Закон Кулона-Амонтона
P
Ff f d N
Сила трения направлена противоположно вектору
скорости движения тела
N
Ff
v
Ff
N
v
v
Ff fd N
v
fd fs
ТРЕНИЕ
2.1.
СКОЛЬЖЕНИЯ
ССС
1.7. ОПРЕДЕЛЕНИЕ
ТРЕНИЕ
73
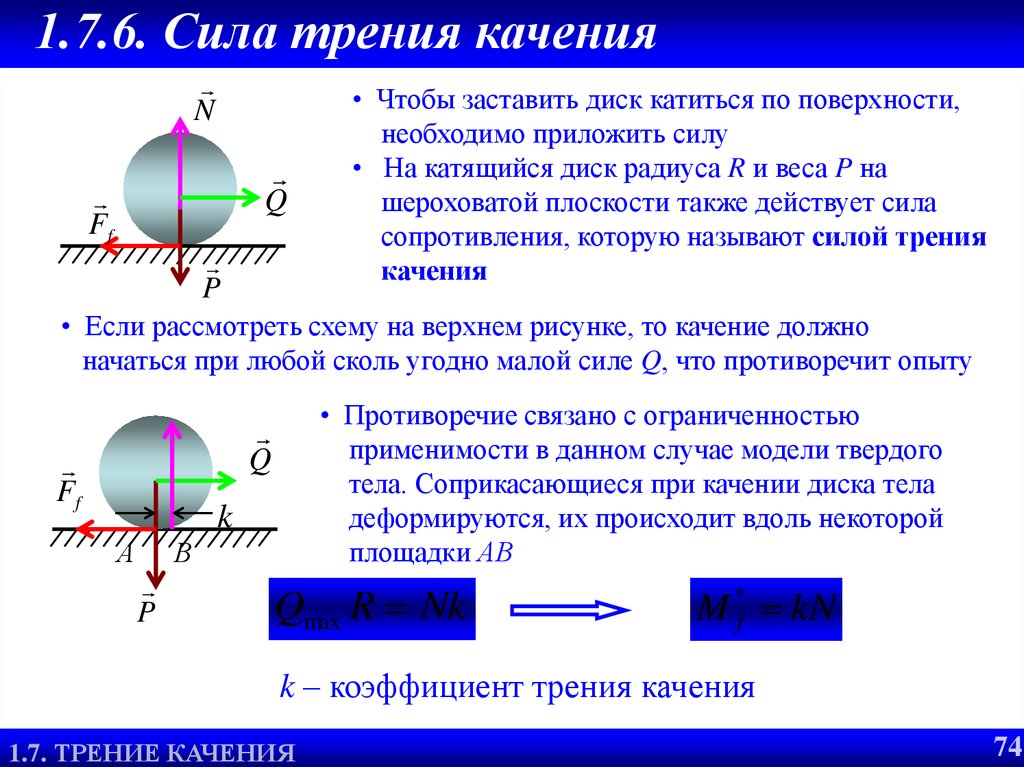
74. 1.7.6. Сила трения качения
NQ
Ff
P
• Чтобы заставить диск катиться по поверхности,
необходимо приложить силу
• На катящийся диск радиуса R и веса P на
шероховатой плоскости также действует сила
сопротивления, которую называют силой трения
качения
• Если рассмотреть схему на верхнем рисунке, то качение должно
начаться при любой сколь угодно малой силе Q, что противоречит опыту
• Противоречие связано с ограниченностью
применимости в данном случае модели твердого
тела. Соприкасающиеся при качении диска тела
деформируются, их происходит вдоль некоторой
площадки АВ
Q
Ff
k
А
В
P
Qmax R Nk
M *f kN
k – коэффициент трения качения
ТРЕНИЕ
2.1.
СКОЛЬЖЕНИЯ
ССС
1.7. ОПРЕДЕЛЕНИЕ
ТРЕНИЕ
КАЧЕНИЯ
74
75. I. Статика
I.8. Расчет плоской фермыи составных тел
75
76. 1.8. Расчет конструкций
• Понятие о ферме• Статически определимые простые плоские
фермы
• Аналитический расчет плоской фермы
• Метод вырезания узлов
• Метод Риттера (сечений)
• Расчет двухсоставной рамы
• Расчет двухсоставных конструкций из балок
1.4.
И РЕАКЦИИ
СВЯЗЕЙ
1.7.СВЯЗИ
СТАТИКА
1.2.
ОСНОВНЫЕ
ПОНЯТИЯ
И МОДЕЛИ
76
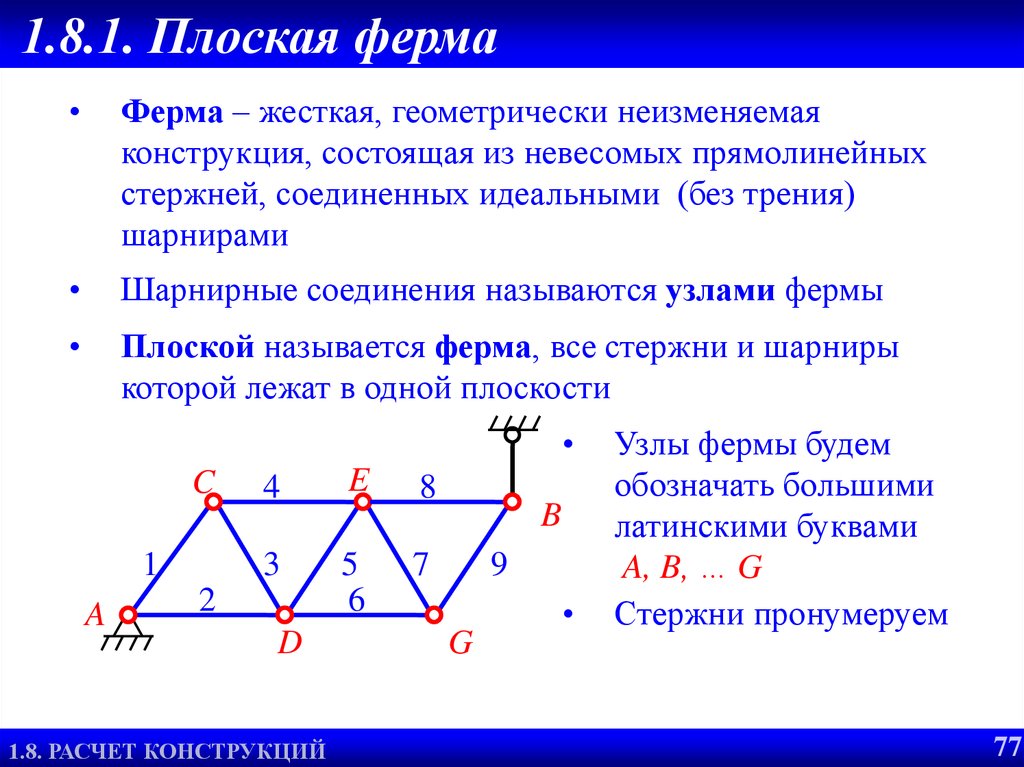
77. 1.8.1. Плоская ферма
Ферма – жесткая, геометрически неизменяемая
конструкция, состоящая из невесомых прямолинейных
стержней, соединенных идеальными (без трения)
шарнирами
Шарнирные соединения называются узлами фермы
Плоской называется ферма, все стержни и шарниры
которой лежат в одной плоскости
C
1
A
4
E
3
5
6
2
D
2.1.
ССС
1.8. ОПРЕДЕЛЕНИЕ
РАСЧЕТ КОНСТРУКЦИЙ
8
B
7
9
G
Узлы фермы будем
обозначать большими
латинскими буквами
A, B, … G
Стержни пронумеруем
77
78. 1.8.2. Расчет плоской фермы
Расчет плоской фермы сводится кнахождению сил реакции опор;
определению усилий в стержнях
фермы методом вырезания узлов
и/или методом сечений ( Риттера)
2.1.
ССС
1.8. ОПРЕДЕЛЕНИЕ
РАСЧЕТ КОНСТРУКЦИЙ
78
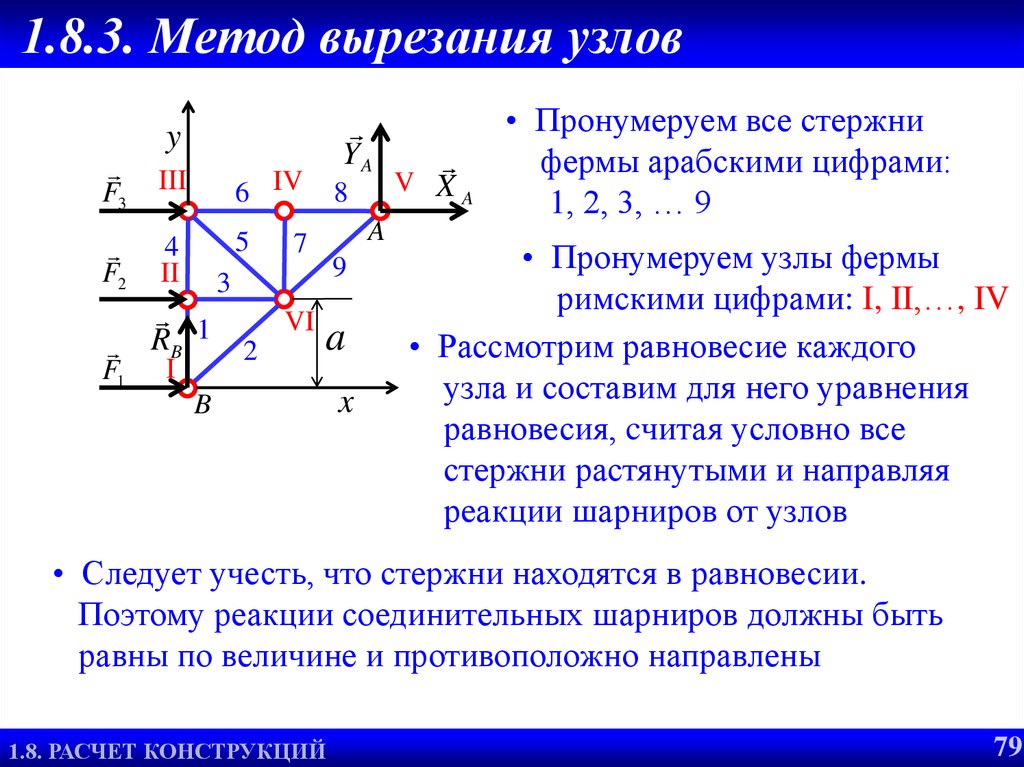
79. Метод вырезания узлов
1.8.3. Методвырезания
узлов
Метод
вырезания
узлов
YA
y
F3
III
6 IV
F2
4
II
5
A
7
9
3
1
VI
R
B
2
F1
8
I
a
B
x
V XA
• Пронумеруем все стержни
фермы арабскими цифрами:
1, 2, 3, … 9
• Пронумеруем узлы фермы
римскими цифрами: I, II,…, IV
• Рассмотрим равновесие каждого
узла и составим для него уравнения
равновесия, cчитая условно все
стержни растянутыми и направляя
реакции шарниров от узлов
• Следует учесть, что стержни находятся в равновесии.
Поэтому реакции соединительных шарниров должны быть
равны по величине и противоположно направлены
2.1.
ССС
ПРИМЕР
РАСЧЕТА
ФЕРМЫ
1.8. ОПРЕДЕЛЕНИЕ
РАСЧЕТ
КОНСТРУКЦИЙ
79
80.
1.8.4. Методсечений
(Риттера)
Метод
сечений
(Риттера)
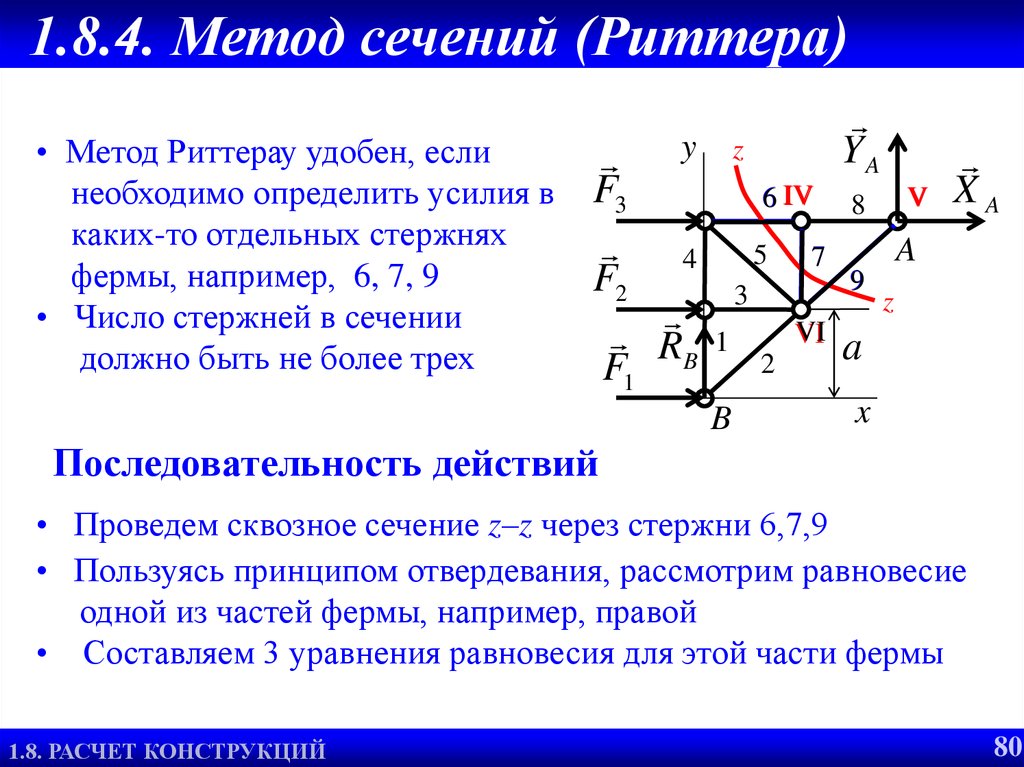
• Метод Риттерау удобен, если
необходимо определить усилия в
каких-то отдельных стержнях
фермы, например, 6, 7, 9
• Число стержней в сечении
должно быть не более трех
y
F3
4
F2
R
F1 B
YA
z
6 IV
5
7
3
1
B
VI
2
V
8
XA
A
9
z
a
x
Последовательность действий
• Проведем сквозное сечение z–z через стержни 6,7,9
• Пользуясь принципом отвердевания, рассмотрим равновесие
одной из частей фермы, например, правой
• Составляем 3 уравнения равновесия для этой части фермы
2.1.
ССС
ПРИМЕР
РАСЧЕТА
ФЕРМЫ
1.8. ОПРЕДЕЛЕНИЕ
РАСЧЕТ
КОНСТРУКЦИЙ
80
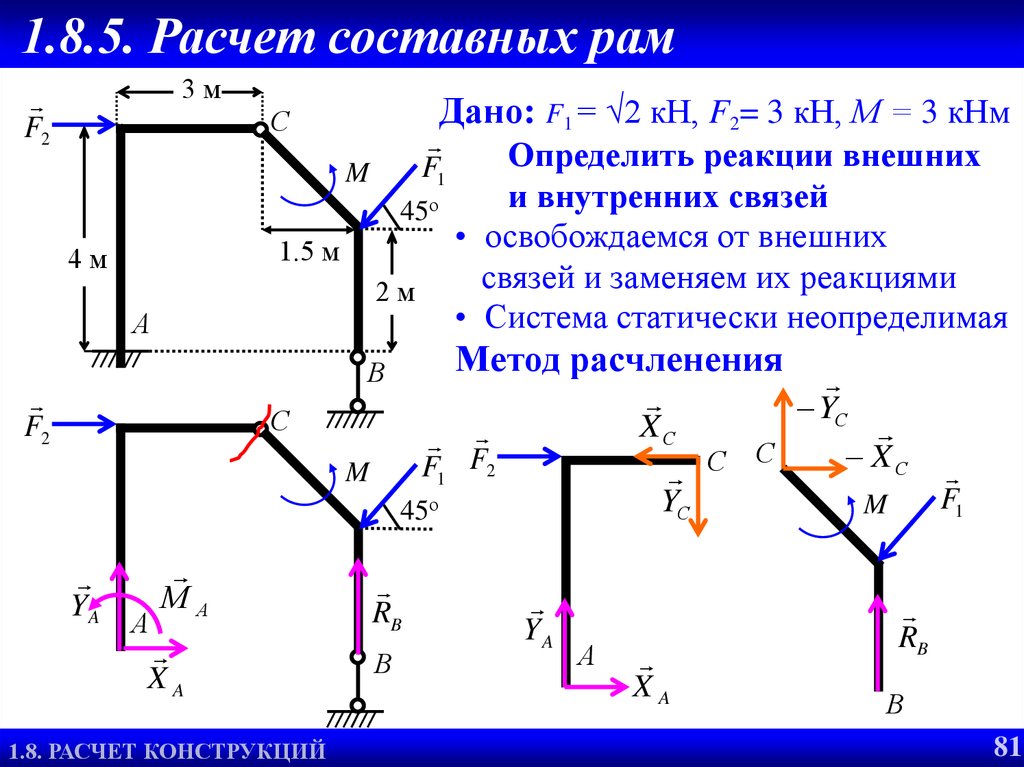
81. 1.8.5. Расчет составных рам
3мF2
Дано: F1 = √2 кН, F2= 3 кН, М = 3 кНм
С
M
1.5 м
4м
А
F1
Определить реакции внешних
и внутренних связей
45о
• освобождаемся от внешних
связей и заменяем их реакциями
2м
• Система статически неопределимая
Метод расчленения
В
F2
С
YС
XС
С
XС
С
F1
YС
M
F1 F2
M
45о
YA
А
МА
XA
2.1.
ССС
1.8. ОПРЕДЕЛЕНИЕ
РАСЧЕТ КОНСТРУКЦИЙ
RB
В
YA
А
XA
RB
В
81
82.
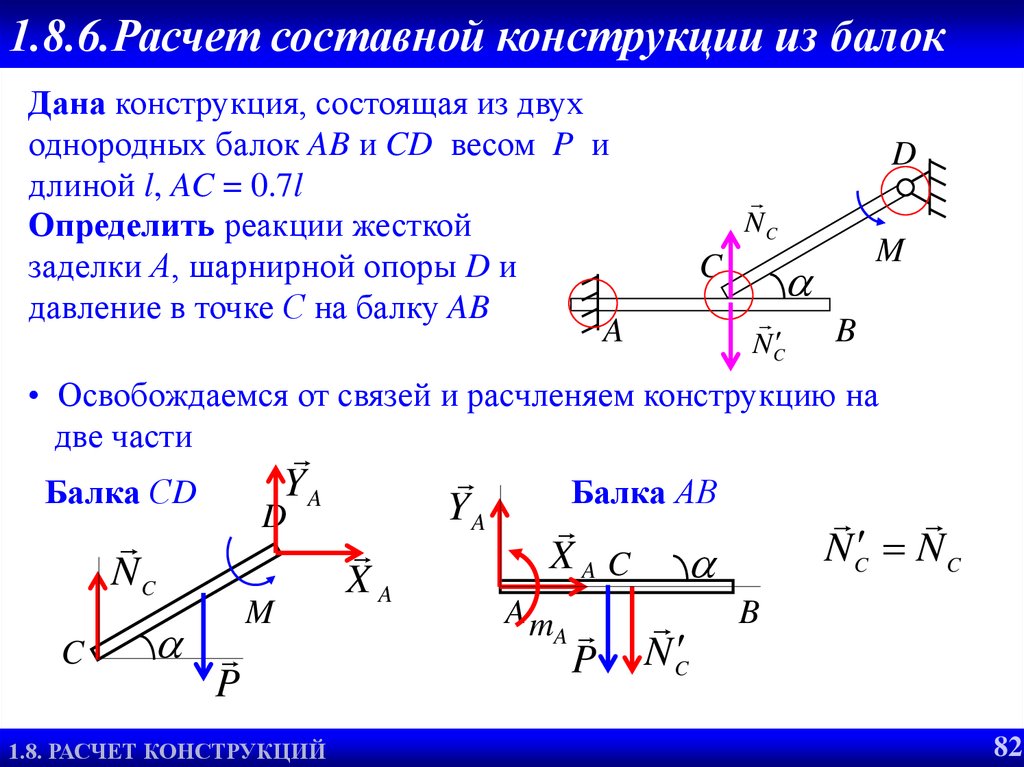
1.8.6.Расчет составной конструкции из балокДана конструкция, состоящая из двух
однородных балок AB и CD весом P и
длиной l, AC = 0.7l
Определить реакции жесткой
заделки А, шарнирной опоры D и
давление в точке С на балку AB
A
D
NC
M
C
N C
B
• Освобождаемся от связей и расчленяем конструкцию на
две части
YA
Балка СD
D
NC
C
M
XA
YA
P
2.1.
ССС КОНСТРУКЦИЙ
РАСЧЕТ
СОСТАВНЫХ
1.8. ОПРЕДЕЛЕНИЕ
РАСЧЕТ
КОНСТРУКЦИЙ
Балка АВ
XA C
Am
A
P
N C N C
N C
B
82
83. II. Кинематика
2.1. Кинематика точки83
84. 2.1. Кинематика точки
• Основные понятия• Задачи кинематики
• Способы задания движения точки
• Траектория точки
• Скорость точки и годограф скорости
• Ускорение точки
• Частные случаи движения точки: прямолинейное
и криволинейное движения.
1.4.
СВЯЗИ
И РЕАКЦИИ
СВЯЗЕЙ
2. КИНЕМАТИКА
1.2.
ОСНОВНЫЕ
ПОНЯТИЯ
И МОДЕЛИ
84
85. 2.1.1. Задачи кинематики
Кинематика – это раздел теоретической механики, вкотором изучается движение тела с геометрической точки
зрения, т.е. без учета сил, действующих на тело
Движение материальной точки – это изменение ее положения
относительно какого-либо другого тела (тела отсчета) с
течением времени
Положение объекта задается расстоянием до некоторого
другого объекта и является относительным. Относительным
является и само движение
Задачи кинематики
1. Определение математических способов задания
движения тела
2. Определение для заданного способа задания движения
тела его кинематических характеристик
2.1. ОПРЕДЕЛЕНИЕ
ССС
КИНЕМАТИКА ТОЧКИ
85
86. 2.1.2. Пространство и время
• Постулируется существование не связанных между собойабсолютного пространства и абсолютного времени
Свойства пространства и времени не зависят и от того, как
движутся тела
Пространство является трехмерным евклидовым пространством,
оно однородное и изотропное
Время также однородное и одинаково во всех точках пространства
Время изменяется непрерывно, а наблюдатель измеряет
"расстояние" между различными моментами времени часами
Часы универсальны и их показания не зависят от того,
расположены они в покоящихся или движущихся объектах
Однородность времени означает отсутствие выделенных моментов
времени. Выбор начала отсчета времени поэтому диктуется лишь
конкретной решаемой задачей
2.1. ОПРЕДЕЛЕНИЕ
ССС
КИНЕМАТИКА ТОЧКИ
86
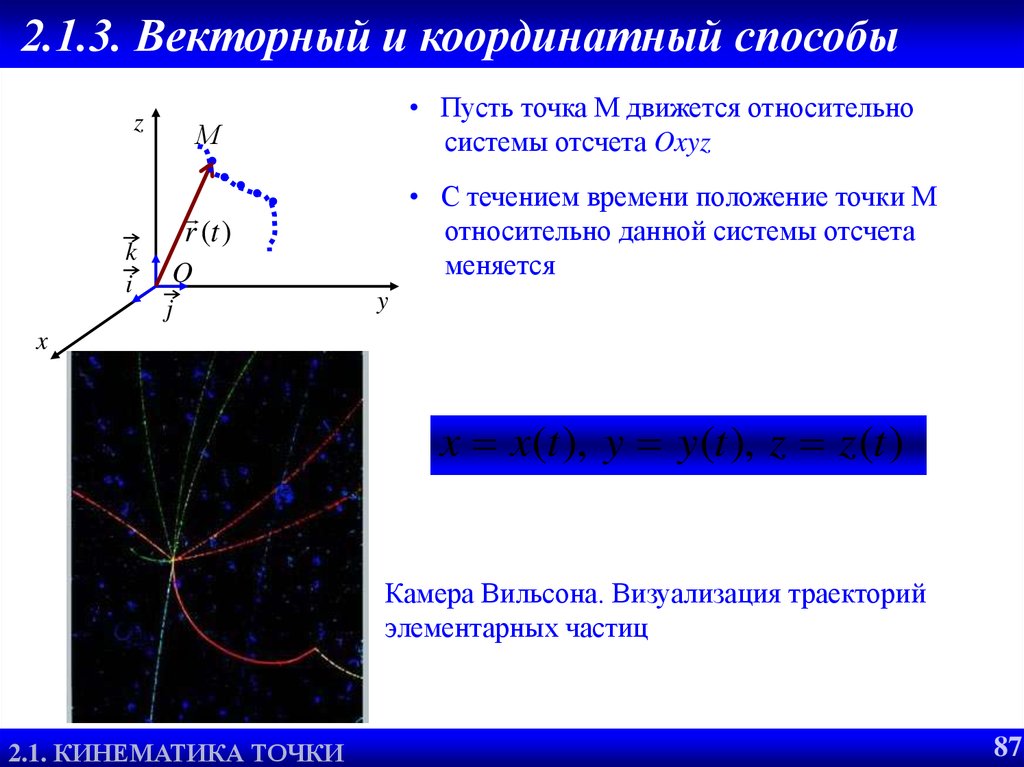
87. 2.1.3. Векторный и координатный способы
zk
i
• Пусть точка М движется относительно
системы отсчета Oxyz
М
• С течением времени положение точки М
относительно данной системы отсчета
меняется
r (t )
O
y
j
x
r r t
x x(t ), y y (t ), z z (t )
Камера Вильсона. Визуализация траекторий
элементарных частиц
2.1.
ССС
ВЕКТОРНЫЙ
СПОСОБ
ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ.
2.1. ОПРЕДЕЛЕНИЕ
КИНЕМАТИКА
ТОЧКИ
87
88.
2.1.4. Естественный способ заданияА
– О
+
s
M
B
s = s(t)
Пусть точка М движется вдоль траектории АВ
Выберем на этой траектории какую-нибудь
точку О, которую примем за начало отсчета
. Будем считать траекторию криволинейной
координатной осью и установим на ней
положительное и отрицательное направления
Введем криволинейную координату s, длину
криволинейного отрезка ОМ, взятую с
соответствующим знаком
Закон движения точки вдоль траектории
M
• Стоит заметить, что уравнение s = s(t)
– +
О
определяет положение точки на
M
s
траектории, а не путь, пройденный ею
M1
Пройденный путь равен
OM1 MM1
2.1.
ССС
ЕСТЕСТВЕННЫЙ
СПОСОБ
ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ.
2.1. ОПРЕДЕЛЕНИЕ
КИНЕМАТИКА
ТОЧКИ
88
89.
2.1.5. Связь естественного и координатного способовz
• Пусть точка M движется вдоль траектории АВ
A
– O
• Приращение траектории s за время t равно
Δs
+ М
Δx
Δz
О
s ( x) 2 ( y ) 2 ( z ) 2
Δy
При t 0
B
s 0, x 0, y 0, z 0
y
x
ds (dx) 2 (dy ) 2 (dz ) 2
• Координаты s, x, y, z – функции времени
dx
dy
dz
dx xdt , dy ydt , dz zdt , где x , y , z
dt
ds
x 2 y 2 z 2
dt
2.1.
• Коэффициент
2.1. ОПРЕДЕЛЕНИЕ
КИНЕМАТИКАССС
ТОЧКИ
dt
dt
t
s(t ) s(0) x 2 y 2 z 2 dt
0
трения покоя
89
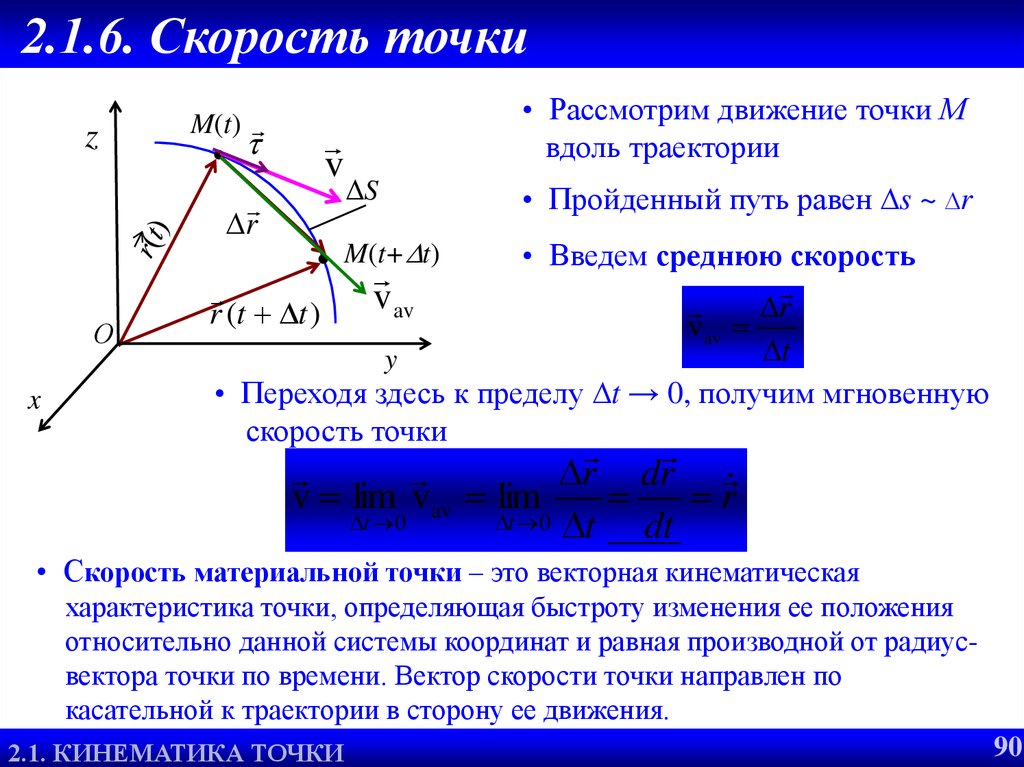
90. 2.1.6. Скорость точки
zM(t)
v
r
О
x
• Рассмотрим движение точки М
вдоль траектории
ΔS
• Пройденный путь равен s ~ r
M(t+ t)
• Введем среднюю скорость
v
r
av
r (t t )
vav
t
y
• Переходя здесь к пределу t → 0, получим мгновенную
скорость точки
r dr
v lim vav lim
r
t 0
t 0 t
dt
• Скорость материальной точки – это векторная кинематическая
характеристика точки, определяющая быстроту изменения ее положения
относительно данной системы координат и равная производной от радиусвектора точки по времени. Вектор скорости точки направлен по
касательной к траектории в сторону ее движения.
2.1.
2.1. ОПРЕДЕЛЕНИЕ
КИНЕМАТИКАССС
ТОЧКИ
90
91. 2.1.7. Ускорение точки
M(t)v(t t )
v
• Как определить быстроту изменения
скорости точки?
• Пусть материальная точка М движется
вдоль траектории
v(t )
M(t+ t)
• Определим приращение скорости за
время t
v
v(t t ) • Определим среднее ускорение aav
t
• Переходя здесь к пределу t → 0, получим мгновенное ускорение
точки
v dv
a lim aav lim
v r
t 0
t 0 t
dt
• Таким образом, ускорение точки – это векторная кинематическая
величина, характеризующая быстроту изменения ее скорости и
равная первой производной от скорости или второй производной от
радиус-вектора по времени
2.1.
2.1. ОПРЕДЕЛЕНИЕ
КИНЕМАТИКАССС
ТОЧКИ
91
92. 2.1.8. Тангенциальное и нормальное ускорение
Т.о.,2
s v
2
a a an s n v n v n ,
2
где ω = v/ρ
a – тангенциальное ускорение, характеризующее изменение
скорости по величине
a n – нормальное ускорение, характеризующее изменение
скорости по направлению
a a 2 an2 v 2 v4 / 2 v 2 4 2
2.1.
2.1. ОПРЕДЕЛЕНИЕ
КИНЕМАТИКАССС
ТОЧКИ
92
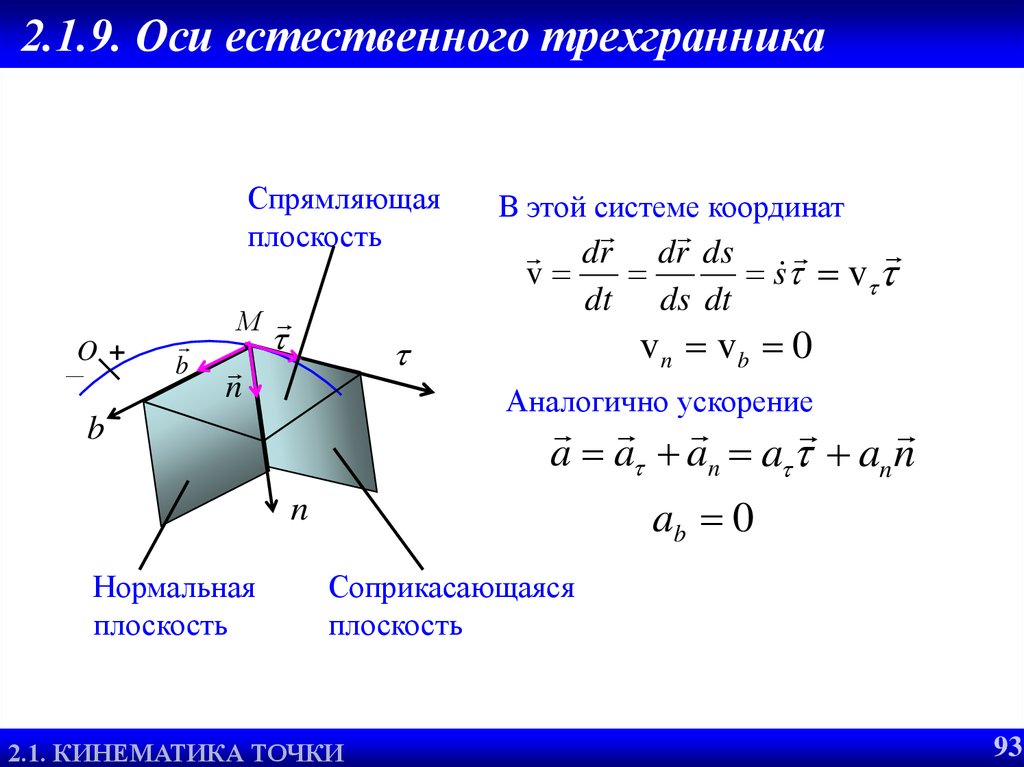
93. 2.1.9. Оси естественного трехгранника
Спрямляющаяплоскость
O +
–
b
М
n
В этой системе координат
dr dr ds
v
s v
dt ds dt
v n vb 0
Аналогично ускорение
a a an a an n
b
ab 0
n
Нормальная
плоскость
Соприкасающаяся
плоскость
2.1.
2.1. ОПРЕДЕЛЕНИЕ
КИНЕМАТИКАССС
ТОЧКИ
93
94. II. Кинематика
2.2. Кинематика ТТ94
95. 2.8. Кинематика ТТ
Задание движения твердого тел
Степени свободы
Поступательное движение твердого тела
Вращение твердого тела вокруг неподвижной оси
Угловая скорость и угловое ускорение
Скорость и ускорение точек твердого тела,
вращающегося вокруг оси
Вращательное и центростремительное ускорения
Равномерное и равноускоренное вращение твердого тела
вокруг оси
Движение твердого тела с одной неподвижной точкой
Сферическое движение
Произвольное движение твердого тела
1.4.
СВЯЗИ
И РЕАКЦИИ
СВЯЗЕЙ
2. КИНЕМАТИКА
1.2.
ОСНОВНЫЕ
ПОНЯТИЯ
И МОДЕЛИ
95
96. 2.2.1. Задание движения ТТ
zr1
rk 1
rk
O
y
x
• Пусть дано твердое тело (ТТ)
• По определению это совокупность
материальных точек, расстояние между
которыми фиксированы и не меняются
со временем
• Закон движения скольки точек нужно
задать, чтобы определить движение ТТ?
• Пусть задан закон движения r1 r1 (t )
• Радиус-вектор произвольной точки k твердого тела равен
rk (t ) r1 (t ) rk1 (t )
• Модуль вектора rk 1 постоянен, но относительная скорость rk1 0
• Таким образом, знание кинематических характеристик одной точки твердого
тела не позволяет определить кинематические характеристики любой другой
его точки
2.1.
ССС
2.2. ОПРЕДЕЛЕНИЕ
КИНЕМАТИКА ТТ
96
97. 2.2.2. Степени свободы
• Положение трех точек твердого тела в произвольный моментвремени характеризуется девятью координатами
xi xi (t ), yi yi (t ), zi zi (t ),
i = 1, 2, 3
Поскольку, однако, в твердом теле расстояния между любыми двумя
его точками постоянны, то эти координаты связаны тремя условиями
( x2 x1 ) 2 ( y 2 y1 ) 2 ( z 2 z1 ) 2 r21
( x3 x1 ) 2 ( y 3 y1 ) 2 ( z 3 z1 ) 2 r31
( x3 x 2 ) 2 ( y3 y 2 ) 2 ( z 3 z 2 ) 2 r32
Число независимых параметров (или координат),
определяющих положение системы в пространстве,
называется числом степеней свободы
2.1.
ССС
2.2. ОПРЕДЕЛЕНИЕ
КИНЕМАТИКА ТТ
97
98. 2.2.3. Поступательное движение ТТ
Поступательным называется такое движение тела, прикотором прямая, соединяющая две любые точки тела, остается
в процессе движения параллельной самой себе
• Очевидно, любое прямолинейное движение твердого тела является
поступательным
А
В
• Однако есть примеры поступательных движений, когда траектории
С вовсе не являютсяDпрямыми линиями
отдельных его точек
• Cпарник АВ при вращении кривошипов АС и BD также
движется поступательно, он остается параллельным самому
себе
2.1.
ССС
2.2. ОПРЕДЕЛЕНИЕ
КИНЕМАТИКА ТТ
98
99. 2.2.4. Теорема о кинематических характеристиках
При поступательном движении твердого тела все его точкиописывают конгруэнтные траектории и имеют в каждый
момент времени одинаковые скорости и ускорения
z
А
rА
rАВ
Доказательство
• Для любых двух точек А и В
В
rВ
O
y
x
rB (t ) rA (t ) rАВ (t )
drB drA drAB drA или
dt
dt
dt
dt
aB (t ) aA (t )
vB (t ) v A (t )
• Таким образом, траектория точки В получается из
траектории точки А простым сдвигом на постоянный
вектор rАВ , это и означает, что траектории конгруэнтны
(при наложении совпадают)
2.1.
ССС
2.2. ОПРЕДЕЛЕНИЕ
КИНЕМАТИКА ТТ
99
100. 2.2.5. Вращательное движение ТТ
z z1A
K
B(t)
φ
• Положение твердого тела полностью определится углом поворота φ этого тела вокруг оси
• Введем подвижную систему координат Ox1 y1 z1 ,
связанную с телом
B(0)
y1
O
φ
x
x1
φ
• Угол поворота φ тогда можно определить как
угол, образуемый между осями в плоскости ху
• При повороте тела на угол φ точка В
y поворачивается вокруг оси также на этот угол
• Закон движения произвольной точки тела определяется
тогда уравнением
(t )
Это уравнение называется законом вращательного
движения твердого тела
2.1.
ССС
ВЕКТОРНЫЙ
СПОСОБ
ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ.
2.2. ОПРЕДЕЛЕНИЕ
КИНЕМАТИКА
ТТ
100
101. 2.2.6. Угловая скорость
z z1A
• Закон движения имеет вид:
B(t)
φ
K
O
• За промежуток времени t тело повернется на
угол φ
B(0)
k
cp
y1
φ
y
φ
x
x1
(t )
t
• Переходя к пределу, получим мгновенную
угловую скорость
d
lim cp lim
t 0
t 0 t
dt
• Угловая скорость измеряется в радианах в секунду или числом
оборотов в минуту
2 n n
60
30
• Вектор угловой скорости ω направлен вдоль оси вращения в сторону,
откуда это вращение видно происходящим против часовой стрелки
k
2.1.
ССС
ВЕКТОРНЫЙ
СПОСОБ
ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ.
2.2. ОПРЕДЕЛЕНИЕ
КИНЕМАТИКА
ТТ
101
102. 2.2.9. Угловое ускорение
• Если за промежуток времени t угловая скорость тела изменяется на ω,то можно ввести среднее угловое ускорение тела за время t
cp
t
• Переходя к пределу, получим мгновенное угловое ускорение
k
d d 2
lim cp lim
2
t 0 t
dt
dt
t 0
• Размерность угловой скорости и углового ускорения: [ ] 1 / c, [ ] 1 / c
z A
z A
O
y
x
2
• Замедленное вращение x
2.1.
ССС
ВЕКТОРНЫЙ
СПОСОБ
ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ.
2.2. ОПРЕДЕЛЕНИЕ
КИНЕМАТИКА
ТТ
O
y
• Ускоренное вращение
102
103. 2.2.10. Скорость и ускорение точек ТТ
Действительно,i
j
rB 0 0
xB
yB
v B RB rB
k
i
j
k
RB 0
0
j xB i y B
zB
yB
0
xB
v B RB
• Определим теперь ускорение точки В
d
d
d
r
B
aBa B rB
rB rB vB rB ( rB )
dt
dt
dt
aBr rB
z A
r
aB
aB
K
Bс
a rB sin( , rB ) RB
– центростремительное
с
aB v B ( rB )
r
B
r aB
ускорение
B
O
x
– вращательное ускорение
y
aBc v B 2 RB
2.1.
ССС
ВЕКТОРНЫЙ
СПОСОБ
ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ.
2.2. ОПРЕДЕЛЕНИЕ
КИНЕМАТИКА
ТТ
103
104. 2.2.11. Вращение относительно произвольной оси
• В общем случае твердое тело может вращаться относительно оси , не совпадающей по направлению ни с одной из осей данной системы координат• Угловая скорость вращения тела вокруг оси l
z
снова можно определить соотношением
A
l ,
l l i l j l k
но
O
x
y
z
x i y j z k , где
x lx , y l y , z lz
l
• Если lx=ly=0, то тело вращается вокруг оси Oz и,
как мы установили, z , где φ – угол поворота
x
тела вокруг этой оси
• Аналогично, если ввести углы поворота тела φx, φy и относительно двух
других осей, то x l x x , y l y y , z l z z
y
Т.о., вращение тела относительно произвольной оси можно представить
как суперпозицию вращений относительно трех осей неподвижной
декартовой системы отсчета
2.1.
ССС
ВЕКТОРНЫЙ
СПОСОБ
ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ.
2.2. ОПРЕДЕЛЕНИЕ
КИНЕМАТИКА
ТТ
104
105. 2.2.12. Передаточные механизмы
14
I
II
A
B
Вал I вращается с угловой скоростью ω1.
Подбирая
можно,
таким
Определитьрадиусы
угловуюколес,
скорость
вращения
образом,
по заданной
угловой
скорости
вала II, если
радиусы колес
(шестерней)
I вала I получить
механизма
равны r1, любую
r2, r3, r4.наперед
заданную скорость II вала II
Решение
2
3
• Колесо 1 жестко скреплено с валом I, поэтому
I = 1
• Аналогично 4 = II
• Приравнивая скорости в точках A и B контакта колес, получим
v A 1r1 2 r2 ,
v B 3 r3 4 r4 .
• Учитывая, что колеса 2 и 3 жестко скреплены, получаем 2 = 3
r1 r3
4
1
r2 r4
7.3. СКОРОСТЬ ТОЧКИ
2.2. КИНЕМАТИКА ТТ
или
II
r1r3
r2 r4
I
105
106. II. Кинематика
2.3. Плоскоедвижение ТТ
106
107. 2.3. Плоское движение ТТ
• Задание движения• Скорости точек тела при плоском движении
• Теорема о проекциях скоростей двух точек тела
• Мгновенный центр скоростей
• Ускорение точек при плоском движении
1.4.
СВЯЗИ
И РЕАКЦИИ
СВЯЗЕЙ
2. КИНЕМАТИКА
1.2.
ОСНОВНЫЕ
ПОНЯТИЯ
И МОДЕЛИ
107
108. 2.3.1. Определение и мотивация
Движение твердого тела называется плоским (плоскопараллельным), если все точки тела движутся в плоскостях,параллельных некоторой неподвижной плоскости
Иллюстрация работы кривошипно-шатунного механизма.
Передача движения колесу
2.1.
ССС ТВЕРДОГО ТЕЛА
2.3. ОПРЕДЕЛЕНИЕ
ПЛОСКОЕ ДВИЖЕНИЕ
108
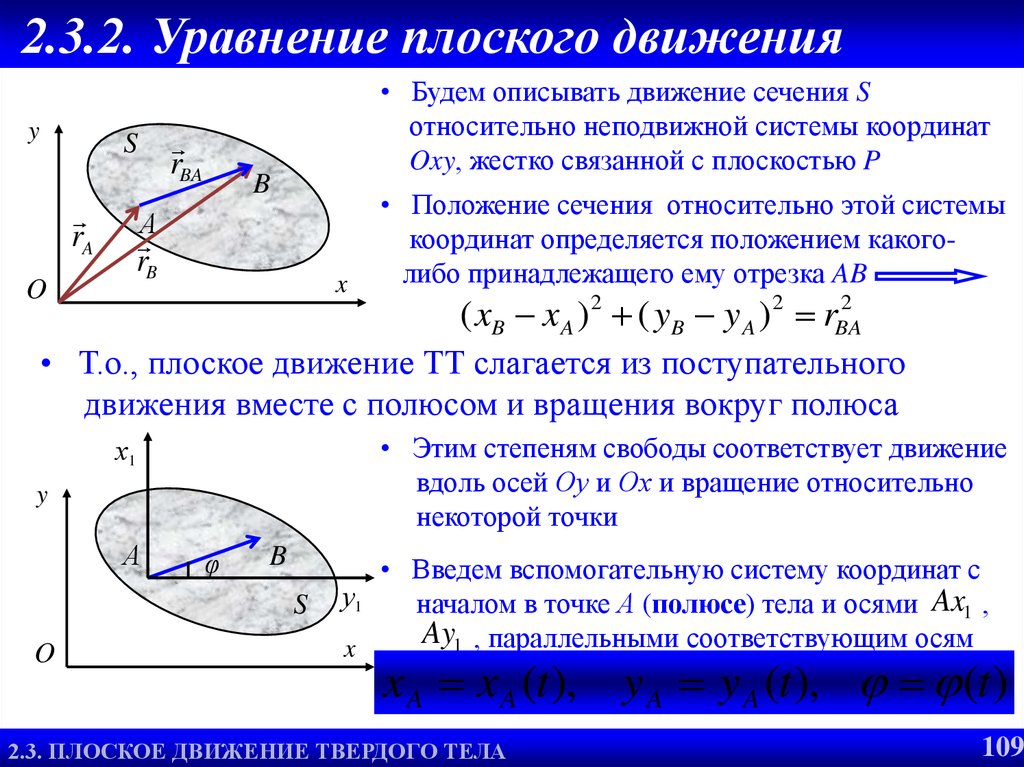
109. 2.3.2. Уравнение плоского движения
yrBA
S
rA
• Будем описывать движение сечения S
относительно неподвижной системы координат
Oxy, жестко связанной с плоскостью P
B
А
rB
O
x
• Положение сечения относительно этой системы
координат определяется положением какоголибо принадлежащего ему отрезка AB
2
( xB x A ) 2 ( yB y A ) 2 rBA
• Т.о., плоское движение ТТ слагается из поступательного
движения вместе с полюсом и вращения вокруг полюса
• Этим степеням свободы соответствует движение
вдоль осей Оу и Ох и вращение относительно
некоторой точки
х1
y
А
φ
B
S
O
• Введем вспомогательную систему координат с
у1
началом в точке А (полюсе) тела и осями Ax1 ,
Ay1 , параллельными соответствующим осям
x
неподвижной системы координат
x A x A (t ), y A y A (t ), (t )
2.3. ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
109
110. 2.3.3. Теорема о скоростях точек ТТ
х1М
y
rM
O
• Скорость произвольной точки М находится
дифференцированием закона движения
φ
rA
А
rM (t ) rA (t ) (t )
у1
x
drA d
v M rM
dt
dt
vM v A vMA
где введена скорость движения точки М относительно полюса А
d
v MA v B
dt
vM v A B
Скорость произвольной точки М ТТ, совершающего плоское
движение, геометрически складывается из скорости какой-нибудь
другой точки А, принятой за полюс, и скорости этой точки в ее
вращении вместе с телом вокруг полюса
2.3. ПЛОСКОЕ ДВИЖЕНИЕ ТТ
110
111. 2.3.4. Теорема о скоростях 2-х точек
vM v A vMAСкорости произвольных двух точек связаны между собой
Следствие 1
Проекции скоростей двух точек сечения S на прямую, их
соединяющую, равны
vМ
• Для доказательства достаточно спроециv МА
vА
ровать уравнение скоростей на прямую
vА
АМ и учесть, что v АМ
MА
М
А
Следствие 2
• Если точки А, В и С сечения S лежат на одной прямой, то концы
векторов скоростей этих точек, тоже лежат на одной прямой,
причем
2.3. КИНЕМАТИКА ПЛОСКОГО ДВИЖЕНИЯ ТТ
111
112. 2.3.5. Теорема о МЦС
Мгновенным центром скоростей (МЦС) сечения тела (или плоскойфигуры) называется точка, скорость которой в данный момент времени
равна нулю
Теорема
Если угловая скорость рассматриваемого сечения S в данный момент
времени отлична от нуля, то мгновенный центр скоростей существует и
единственен
Действительно, рассмотрим сечение S
• Пусть в некоторый момент времени t точки A и B
имеют скорости, не параллельные друг другу
• Это следует из теоремы
о проекциях скоростей, так
B
vА
как если бы скорость vС была отлична от нуля, то
А
S
она одновременно должна была бы быть перпенди
vB
кулярна к АА’ и BB’. Последнее, однако,
C
невозможно в силу непараллельности скоростей
точек А и В
B’
А’
Теорема доказана
2.3. ПЛОСКОЕ ДВИЖЕНИЕ ТТ
112
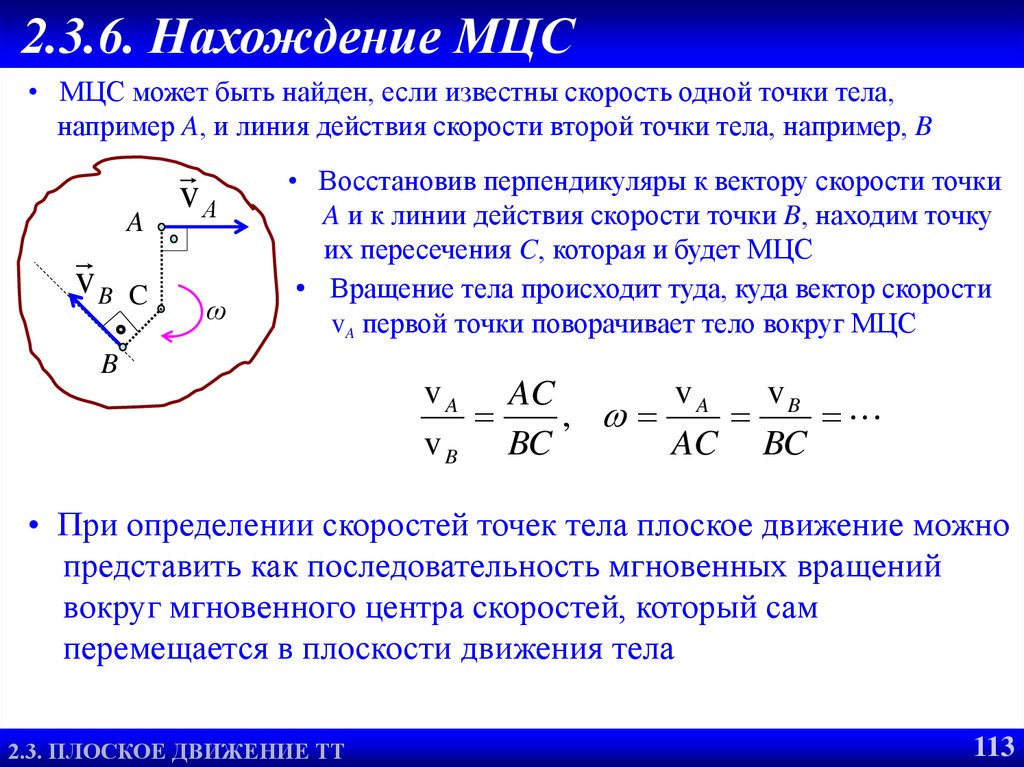
113. 2.3.6. Нахождение МЦС
• МЦС может быть найден, если известны скорость одной точки тела,например A, и линия действия скорости второй точки тела, например, B
vB
A
C
vА
ω
• Восстановив перпендикуляры к вектору скорости точки
A и к линии действия скорости точки B, находим точку
их пересечения C, которая и будет МЦС
• Вращение тела происходит туда, куда вектор скорости
vA первой точки поворачивает тело вокруг МЦС
B
v A AC
vA
vB
,
v B BC
AC BC
• При определении скоростей точек тела плоское движение можно
представить как последовательность мгновенных вращений
вокруг мгновенного центра скоростей, который сам
перемещается в плоскости движения тела
2.3. ПЛОСКОЕ ДВИЖЕНИЕ ТТ
113
114. 2.3.7. Теорема о сложении ускорений точек
Ускорение любой точки тела, совершающего плоское движение,определяется
как сумма
полюса
и ускорения данной
Теорема
о ускорения
сложении
ускорений
точки во вращательном движении вокруг полюса
aB aA aA aВA
Доказательство
aA
A
aВ
dv B d
dv A d d
aB
v B
dt
dt
dt
dt
dt
n
aA
aA a A aBA aBA
aВA
n
aBA
B
aBA
n
aBA , aBA vBA
a BA AB,
a nBA v BA 2 AB
a BA (a nBA ) 2 (a BA ) 2 AB 4 2
Теорема доказана
2.3. ПЛОСКОЕ ДВИЖЕНИЕ ТТ
114
115. Литература
1.2.
3.
4.
Рудяк В.Я., Юдин В.А. Лекции по теоретической
механике. Часть I. Статика и кинематика. Новск. 2004
Рудяк В.Я., Юдин В.А. Сборник
индивидуальных заданий по теоретической
механике. Статика. Нов-ск. 2004
Бутенин Н.Н., Лунц Я.Л., Меркин Д.Р. Курс
теоретической механики. М. 2008
Тарг С.М. Краткий курс теоретической
механики. М. 2008
1.3.
АКСИОМЫ
ЗАКЛЮЧЕНИЕ
1.2.
ОСНОВНЫЕСТАТИКИ
ПОНЯТИЯ И МОДЕЛИ
115





















































































 physics
physics








