Similar presentations:
Теоретическая механика. Статика
1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Статика2. Содержание
Лекция 1. Введение. Основные понятия. Аксиомы статики. Связи и реакции связей.Лекция 2. Система сходящихся сил. Теорема о трех силах. Аналитическое определение
равнодействующей сходящихся сил. Уравнения равновесия.
Лекция 3. Произвольная плоская система сил. Момент силы относительно точки. Пара сил. Теоремы о
парах. Метод Пуансо. Главный вектор и главный момент. Уравнения равновесия. Три формы уравнений
равновесия. Теорема Вариньона.
Лекция 4. Плоские фермы. Методы расчета. Метод вырезания узлов. Метод Риттера. Понятие о линиях
влияния опорных реакций и усилий. Равновесие сочлененных тел. Условие равновесия рычага.
Условие устойчивости тела на опрокидывание. Кинематический способ определения реакций (принцип
возможных перемещений).
Лекция 5. Трение скольжения. Основные законы. Способы определения коэффициента трения. Угол
трения. Конус трения. Учет сил трения при решении задач на равновесие. Сопротивление при качении.
Лекция 6. Произвольная пространственная система сил. Моменты силы относительно центра и оси.
Связь момента силы относительно точки и момента силы относительно оси. Теоремы о парах.
Сложение произвольно расположенных сил в пространстве. Главный вектор и главный момент.
Лекция 7. Аналитическое определение главного вектора и главного момента. Уравнения равновесия
произвольной пространственной системы сил. Возможные случаи приведения системы. Зависимость
главного момента от выбора центра приведения. Инварианты системы. Теоремы Вариньона.
Лекция 8. Сложение параллельных сил. Центр параллельных сил. Центр тяжести. Определение
положения центра тяжести однородных тел. Центры тяжести простейших фигур. Способы определения
положения центров тяжести.
Рекомендуемая литература
1. Яблонский А.А. Курс теоретической механики. Ч.1. М.: Высшая школа. 1977 г. 368 с.
2. Тарг С.М. Краткий курс теоретической механики. - М.: Высшая школа. 2006 г.
3. Мещерский Н.В. Сборник задач по теоретической механике. - М.: Наука. 2006 г.
4. Яблонский А.А. и др. Сборник задач для курсовых работ по теоретической механике.- М.: Высшая школа. 2005 г.
5. Пирогов С.П. Конспект лекций по теоретической механике. Из-во ТюмГНГУ, 2005. - с.107
6. Бондаренко А.Н. Демонстрационная программа “Теория пар” - www.miit.ru/institut/ipss/faculties/trm/main.htm, 2004 г.
7. Бондаренко А.Н. Программа-тренажер “Определение проекции и момента силы” –
www.miit.ru/institut/ipss/faculties/trm/main.htm, 2004 г.
8 Программное обеспечение: http://educon.tsogu.ru:8081.
9. Базы данных, информационно-справочные и поисковые системы: http://educon.tsogu.ru:8081.
3. Р А З Д Е Л П Е Р В Ы Й СТАТИКА ТВЕРДОГО ТЕЛА Глава I. ВВЕДЕНИЯ
РАЗДЕЛ ПЕРВЫЙСТАТИКА ТВЕРДОГО ТЕЛА
Глава I. ВВЕДЕНИЯ
ЛЕКЦИЯ 1
Введение.
Основные понятия.
Аксиомы статики.
Несвободное твердое
тело, связи и реакции
связей.
4. Лекция 1
ВВЕДЕНИЕ. Теоретическая механика (ТМ.) является наукой, в которой изучаются движения тел в пространстве с течениемвремени. Под названием «механика» объединяется ряд наук, изучающих механическое движение и механическое
взаимодействие твердых и деформируемых тел, а также жидких и газообразных сред. ТМ служит базой других разделов
механики, например: (рис.).
Механика
Прикладная механика
Гидромеханика
Аэромеханика
Динамика сооружений
Механика корабля
Строительная механика
Строительные конструкции
Сопротивление материалов
Гидродинамика
Детали машин
Небесная механика
Механика грунтов
Мосты и тоннели
Теория механизмов и машин
Теоретическая механика
Механическое движение – один из видов движения материи, выражающееся в изменении с течением времени взаимных
положений тел или их частей.
Механическое взаимодействие – один из видов взаимодействия материи, вызывающий изменение механического
движения тел или их частей, а также препятствующий изменению их взаимных положений.
Теоретическая механика – изучает законы механического движения и механического взаимодействия, общие для любых
материальных тел.
В основе теоретической механике, как и всякий науки, лежат представления и абстракции, отражающие наиболее важных
особенностей или главные черти изучаемых явлений..
Рассмотрим некоторые основные абстрактные образы ( теоретические модели) материальных тел и систем:
Материальная точка (МТ) – не имеет размеров, но в отличие от геометрической точки обладает массой, равной массе того
тела, которое изображается данной материальной точкой.
Абсолютно твердое тело (АТТ) – система МТ, в которой расстояние между ними не изменяются ни при каких воздействиях.
Механическая система (МС) – совокупность МТ или АТТ, связанных между собой общими законами движения или
взаимодействия.
В зависимости от условия задачи и выбора объекта изучения одно и то же физическое тело может быть принято за МТ, АТТ или МС.
Например, Земля при изучении ее движения вокруг Солнца принимается за МТ, а при изучении ее вращения вокруг собственной оси –
1
за АТТ. При изучении явлений, происходящих на Земле (приливы и отливы, перемещения коры и т.п.), Земля рассматривается как МС.
5. Лекция 1 (продолжение – 1.2)
ТМ. состоит из трех разделов:Теоретическая механика (ТМ)
Статика
Кинематика
Динамика
Статика – изучает равновесие сил, приложенных к твердым тел и способы сложения сил. Для осуществления равновесия
необходимо определенное соотношение сил, поэтому в статике изучаются общие свойства сил, правила замены сил другими
силами, эквивалентными с точки зрения равновесия.
Кинематика –изучает механическое движение материальных тел без учета сил (причин), вызывающих это движение.
Динамика – изучает механическое движение материальных тел в зависимости от причин, его вызывающих. Таким
образом, изучается связь между движением и действующими силами.
Раздел I. СТАТИКА ТВЕРДОГО ТЕЛА
■ 1. Основные понятия теоретической механики
Сила – мера механического взаимодействия. Сила моделируется вектором, характеризуемым направлением и величиной.
Кинематическое состояние тела – состояние покоя или движения с неизменными параметрами.
Система сил – совокупность сил, приложенных к рассматриваемому объекту.
Равнодействующая – сила, эквивалентная системе сил, т.е. не изменяющая кинематическое состояние.
Эквивалентная система сил – заменяет данную систему сил без изменения кинематического состояния объекта.
Взаимно уравновешенная система сил – под ее действием объект находится в равновесии.
■
2. Аксиомы статики
1. Аксиома инерции – Под действием взаимно уравновешенной системы сил тело находится в состоянии покоя или
равномерного прямолинейного движения.
2. Аксиома двух сил – Если тело под действием двух сил находится в равновесии, то эти силы равны по модулю и
направлены по одной прямой в противоположные стороны. Такие две силы представляют собой простейшую взаимно
уравновешенную систему сил.
F1
F2
F1 F2
3. Аксиома присоединения – Если к заданной системе сил присоединить (или изъять) взаимно уравновешенную систему
сил, то кинематическое состояние тела не изменится.
F1
F2
F4
F3
F2
F1
F5
F3
F4 F5
( F1 , F2 , F3 ) ( F1 , F2 , F3 , F4 , F5 )
2
6.
Лекция 1 (продолжение – 1.3)Аксиомы статики (продолжение)
Следствие из аксиомы присоединения – Кинематическое состояние тела не изменится, если силу перенести по линии ее
действия.
F2 F3
F1
F2
F1
F3
F1 F3
F2
( F1 ) ( F1 , F2 , F3 ) ( F2 )
4. Аксиома параллелограмма – Равнодействующая двух пересекающихся сил равна диагонали параллелограмма,
построенного на этих силах как на сторонах.
F1
F2
R
F1
R F1 F2
R F12 F12 2 F1 F2 cos( F1 , F2 )
F2
5. Аксиома действия и противодействия – Всякому действию соответствует равное и противоположное противодействие
(III закон Ньютона).
F
F
12
21
F12 F21
6. Аксиома отвердевания – Равновесие деформируемого тела (нетвердого тело) сохраняется при его затвердевании
(обратное справедливо не всегда).
3. Связи и реакции связей
Свободное твердое тело – свобода перемещений тела не ограничивается никакими другими телами.
Несвободное твердое тело – его движение ограничено другими телами.
Связь – тело, ограничивающее свободу перемещений объекта.
Реакция связи – сила, с которой связь действует на твердое тело .
Принцип освобождаемости от связи – несвободное тело можно рассматривать как свободное, если отбросить связи и
заменить их действие соответствующими реакциями.
3
7.
Лекция 1 (продолжение – 1.4)Связи и реакции связей (продолжение)
Виды связей и их реакции:
2. Абсолютно гладкая поверхность:
1. Нить, шарнирный стержень:
R
Реакция нити
(стержня)
направлена
по нити
(по стержню).
R
R1
R3
Реакция гладкой поверхности
направлена перпендикулярно общей
касательной плоскости, проведенной
к соприкасающимся поверхностям
тела и связи.
R2
3. Неподвижный цилиндрический шарнир:
Rу
R
R
Rx
4. Подвижный цилиндрический шарнир:
Реакция
неподвижного
Реакцию
шарнира проходит
неподвижного
через центр шарнира
шарнира
можно
перпендикулярно
разложить
наидве
оси шарнира
имеет
составляющие,
произвольное
например,
Rx и Ry,
направление.
параллельные
координатным осям.
R
Реакция подвижного
шарнира проходит
через центр шарнира
перпендикулярно
оси шарнира и
плоскости опирания.
Общее правило для связей любого вида:
В жесткой плоской заделке
6. Жесткая
плоская одному
заделка:или
возникает
три реактивных
Если связь
препятствует
нескольким
усилия:
две
составляющие
перемещениям (максимальное число перемещений
– три
5. Неподвижный сферический шарнир:
Реакция
реактивные
силы
Rx и Ry, а
поступательных
и
три
вращательных),
то
по
направлению
Реакцию
неподвижного
также реактивный момент
Ry
Rz
именно этих
этих перемещений
возникают
M A и только
неподвижного
сферического
(пара сил) MA .
соответствующие
реакции
(силы
и
моменты).
R
сферического
шарнира
шарнира проходит
Ry
Rx
можно
на
черезразложить
центр шарнира
три
составляющие,
и имеет
например,
Rx, Ry, Rz,
произвольное
параллельные
направление в
координатным
пространстве.осям.
A
Rx
4
8. Глава II. ПЛОСКАЯ СИСТЕМА СИЛ.
ЛЕКЦИЯ 2Система сходящихся
сил.
Теорема о трех силах.
Аналитическое
определение
равнодействующей
сходящихся сил.
Уравнения равновесия
сил.
9.
Лекция 2F1
F2
Глава I. ПЛОСКАЯ СИСТЕМА СИЛ.
1. Система сходящихся сил. Сходящимся называется силы линии действия
которых пересекаются в одной точке. Точка называется центром системы.
План исследования системы сил соответствует последовательному решению
трех вопросов:
1. Как упростить систему?
2. Каков простейший вид системы?
3. Каковы условия равновесия системы?
R1, 2,3
R1, 2
R1, 2,3, 4
F3
1. Перенесем все силы по линии их действия в точку пересечения (кинематическое
состояние тела при этом не изменится – следствие из аксиомы присоединения).
Сложим первые две силы F1 и F2 (аксиома параллелограмма).
Количество сил уменьшилось на единицу:
Сложим полученную равнодействующую R12 со следующей силой F3.
Количество сил вновь уменьшилось на единицу:
Повторим эту же операцию со следующей силой F4.
Осталась всего одна сила, эквивалентная исходной системе сил:
R1, 2 F1 F2
R1, 2,3 R1, 2 F2
F4
R1, 2,3, 4 R1, 2,3 F4
Сложение сил построением параллелограммов можно заменить построением силового треугольника – выбирается одна
из сил или изображается параллельно самой себе с началом в любой произвольной точке, все другие силы
изображаются параллельными самим себе с началом, совпадающим с концом предыдущей силы.
Результатом такого сложения является вектор, направленный из начала первой силы к концу последней из сил.
2. Простейший вид системы это сила, приложенная в точке пересечения исходных сил.
Сходящаяся система сил приводится к одной силе – равнодействующей (силе,
R F1 F2 F3 F4
эквивалентной исходной системе сил), равной геометрической сумме сил системы:
3. Если равнодействующая системы оказывается не равной нулю, тело под действием такой системы силы
будет двигаться в направлении равнодействующей (система сил не уравновешена). Для того, чтобы
уравновесить систему достаточно приложить силу, равную полученной равнодействующей и
направленной в противоположную сторону (аксиома о двух силах). Таким образом, условием
равновесия системы сходящихся сил является обращение равнодействующей в ноль.
Это условие эквивалентно замкнутости силового треугольника определенным
образом, а именно, направление всех сил при обходе по контуру не изменяется по
направлению:
... Fi
R Fi 0
5
10.
Лекция 2 (продолжение – 2.2)F1
1.1. Теорема о трех силах. Если тело, под действием трех непараллельных сил находится
в равновесии, то линии действия этих сил пересекаются в одной точке. Любая уравновешенная
система трех сил всегда будет плоской. Доказательство:
F3
1. Перенесем две силы по линии их действия в точку их пересечения (кинематическое состояние
тела при этом не изменится – следствие из аксиомы присоединения).
2. Сложим эти силы (аксиома параллелограмма). Теперь система состоит всего из двух сил. А такая
система находится в равновесии, если эти силы равны между собой и направлены по одной линии
в противоположные стороны. Таким образом, все три силы пересекаются в одной точке.
Теорема о трех силах может применяться для определения направления одной из двух реакций тел:
Реакция подвижного шарнира RB направлена вертикально (перпендикулярно
опорной плоскости). Направление (угол наклона к горизонту) реакции
F D
RA
C
неподвижного шарнира RA пока не определено.
RB
Если тело под действием трех сил F, RA и RB находится в равновесии,
RB h
то все три силы должны пересекаться в одной точке (в точке С):
A
B
Действительные направления и величины реакций легко определяются
построением силового треугольника и использованием подобия
треугольников
F1
R12
F2
F2
F
RA
1.2*. Равновесие системы сходящихся сил
(Аналитическое определение равнодействующей сходящихся сил )
l
Каждая из сил, геометрическая сумма которых дает равнодействующую, может быть
представлена через ее проекции на координатные оси и единичные векторы:
Fi
Тогда равнодействующая выражается через проекции сил в виде:
Zi
X i i Yi j Z i k
R ( X 1 X 2 ...)i (Y1 Y2 ...) j (Z1 Z 2 ...)k Rx i R y j Rz k
Fi , yz
Fi
Fi , xz
i
Группировка по ортам дает выражения для проекций равнодействующей:
R
Отсюда
cos( R , x) x ;
Направляющие
R
проекции
Ry Yi ; косинусы
равнодействующей:
Ry
;
Rz Z i . равнодействующей: cos( R , y )
R
Аналитически модуль
R
равнодействующей прос2
2
2
cos( R , z ) z .
R
R
R
R
x
y
z
R
транственной системы сил:
R A F 2 RB2
z
R Fi F1 F2 .... X 1i Y1 j Z1k X 2 i Y2 j Z 2 k ...
Rx X i ;
RB h
F
l
Xi
k
Yi
y
j
x
Fi , xy
Уравнения равновесия сходящейся системы сил
Условие равновесия:
Отсюда
X i 0;
Равнодействующая
уравнения
должна обращаться в
Yi 0;
R 0 равновесия:
ноль:
Для равновесия пространственной системы
Z i 0.
сходящихся сил необходимо и достаточно,
чтобы суммы проекций этих сил на каждую
6
из трех координатных осей были равны нулю.
11.
Лекция 2 (продолжение – 2.2, доп. матер. 1.2*)Проекция силы на ось
Рассмотрим аналитического (численного) метода решения задач статики. Этот метод основывается на
понятии о проекции силы на ось. Проекцией силы на ось есть скалярная величина, равная произведению
модуля силы на косинус угла между силой и положительным направлением оси (рис.).
Проекция имеет знак.
Из рисунки видно, что: Fx =AB1 =ab, Qx= –ED1 = –ed.
Следовательно,
AB1 = Fcosα, ED1 = Qcosφ = – Qcosα1.
Fx = Fcosα, Qx= –Qcosφ = Qcosα1.
Если угол (α) острый, – проекция
положительна, если тупой, – отрицательна, а
если сила перпендикулярна оси, – ее проекция
на ось равна нулю. Проекции силы на любые
параллельные и одинаково направленные оси
равны друг другу.
Проекция силы на плоскость
Проекцией силы на плоскость Оху называется вектор, заключенный между проекциями начала и конца силы
на эту плоскость (рис.).
В отличие от проекции силы на ось, проекция силы на плоскость есть
величина векторная. Поэтому он характеризуется численным значением и
направлением в плоскости Оху, и модулю равно: Fxу = Fcosθ, где θ – угол
между вектором F и ее проекции Fxу.
В некоторых случаях для нахождения проекции силы на ось бывает удобнее
найти сначала ее проекции на плоскость, в которой эта ось лежит, а затем
найденную проекцию на плоскость спроектировать на данную ось.
Например, Fx = Fxу∙cosφ = F∙cosθ∙cosφ,
Fу = Fxу∙sinφ = F∙cosθ∙ sinφ.
6
12. Глава II. ПЛОСКАЯ СИСТЕМА СИЛ.
ЛЕКЦИЯ 3Произвольная плоская
система сил.
Момент силы относительно
центра (или точки).
Пара сил. Теоремы о парах.
Метод Пуансо.
Главный вектор и главный
момент.
Уравнения равновесия.
Три формы уравнений
равновесия.
Теорема Вариньона.
13. Лекция 3
2. Произвольная плоская система сил. Силы лежат в одной плоскости и их линии действия не пересекаются в одной точке.Для рассмотрения такой системы сил необходимо ввести новые понятия:
1. Момент силы относительно точки на плоскости.
2. Пара сил. Момент пары сил.
F
Вращательный эффект силы характеризуется ее моментом, т.е. момент это сила
кручения и является мерой вращательного действия.
h
1. Момент силы относительно точки (центра) на плоскости – алгебраическая величина,
равная произведению модуля силы на плечо, взятая со знаком + (плюс), если вращение плоскости
M A (F ) F h
под действием силы происходит против часовой стрелки, и со знаком – (минус) в противном случае.
A
Плечо силы – длина перпендикуляра, опущенного из точки (центра) на линию действия силы.
. 2. Парой сил называется две силы, равные по величине, параллельные и направленные
в противоположные стороны. Пара сил не может быть упрощена (не может быть заменена одной
F F
силой) и представляет собой новую силовую характеристику механического взаимодействия. Под
действием пары сил, тело начнет вращаться. Вращательный эффект определяется моментом пары.
F
b
Момент пары сил на плоскости (теорема о моменте пары сил) – не зависит от выбора центра (или
полюса) и равен произведению модуля любой из сил пары на плечо пары, взятым со знаком +
d
(плюс), если вращение плоскости под действием пары сил происходит против часовой стрелки, и со
a
знаком – (минус) в противном случае. Мерой действия пары сил является ее моментом.
F
Плечо пары сил – расстояние b или d между линиями действия сил.
A
Вектор момента пары сил направлено перпендикулярно плоскости, в которой расположена пара.
M A ( F , F ) F h
2.1. Теоремы об эквивалентности и о сложение пар: (Теоремы приводятся без доказательств).
1. В независимости момента пары от выбора полюса (точки) можно убедиться вычислением
суммы моментов от каждой из сил относительно любого центра.
M A ( F , F ) F (a b) F a Fb Fd
2. О переносе пары сил в плоскости ее действия. Не нарушая состояния твердого тела, пару сил можно перемещать в любое
место в плоскости ее действия. Кинематическое состояние тела не изменится.
3. Об эквивалентности пар сил. Пары сил, моменты которых равны, эквивалентны. Кинематическое состояние тела не изменится.
M ( F1 , F1 ) F1d1 , M ( F2 , F2 ) F2 d 2 ;
F1d1 F2 d 2 ( F1 , F1 ) ( F2 , F2 )
4. О сложении пар сил на плоскости. Система нескольких пар сил на плоскости эквивалентна одной паре, момент которой равен
алгебраической сумме моментов данных пар. Кинематическое состояние тела не изменится.
Условие равновесия системы пар сил:
M Mi 0
7
14. Лекция 3 (продолжение – 3.2)
2.2. Теорема о параллельном переносе силы (метод Лемма Пуансо). Одной из основных задач статики, является заменаодной системы сил другой – эквивалентной ей. Силу можно перенести параллельно самой себе в любую точку плоскости, если
добавить соответствующую пару сил, момент которой равен моменту этой силы относительно рассматриваемой точки.
Добавим к системе
в точке
две силы, равные
посиле,
величине
между собой
и направленные по
Сходящаяся
система
силAприводится
к одной
приложенной
в центре
F
одной прямойкоторая
в противоположные
стороны равнодействующей,
и параллельные заданной
приведения,
ранее называлась
но силе:
теперь эта сила не
M ( F , F )
F
F F F
заменяет исходную систему сил, поскольку после приведения возникла система пар.
Кинематическое состояние не изменилось (аксиома о присоединении).
Система
к одной паре
о сложении
пар), момент
которой
Исходная пар
силаприводится
и одна из добавленных
сил (теорема
противоположно
направленная
образуют
пару сил.
равен
алгебраической
сумме
моментов
исходных
сил
относительно
центра
Момент пары численно равен моменту исходной силы относительно центра приведения.
приведения.
d
F
M ( F , F ) F d F h M A ( F )
A
Во многих случаях пару сил удобно изображать дуговой стрелкой.
2.3. Приведение к одному центру сил, произвольно расположенных на плоскости. На твердое тело действует система сил,
,
, лежащих в одной плоскости. Возьмем в этой плоскости произвольную точку А и перенесем по методу Пуансо все силы
в эту точку. Вместо исходной произвольной системы получим сходящуюся систему сил и систему пар.
Доказали теорему: Всякая произвольная плосF2
кая система сил, действующих на абсолютно
твердое тело, приводится к одной силе,
F1
называемой главным вектором R и к паре с
h h2
F3 1
моментом, равным главному моменту всех сил
F3
h3
*
M
F1
R
O системы M относительно центра приведения:
F2
F2
- главный вектор,
*
F1
A
R Fi
F3
A
M M A M iA
- главный момент.
2.4. Условия равновесия плоской произвольной системы сил. Условием равновесия плоский произвольной системы сил является
одновременное обращение главного вектора и главного момента системы в ноль:
M M M 0
R* F 0
i
A
iA
Из этого условия следует уравнения равновесия произвольной плоской системы сил, которые можно записать в трех формах.
Уравнения равновесия (I форма) получаются в виде системы трех уравнений из условий равновесия с использованием выражений
для проекций главного вектора:
X i 0;
M iC 0; C
X i 0; x
Существуют еще две
формы уравнений
Yi 0;
M iB 0;
M iB 0;
Равновесия (II и III формы):
8
M iA 0
M iA 0 AB
M iA 0 AB
15. Лекция 3 (продолжение – 3.3)
M iC 0; CX i 0;
II и III формы уравнений равновесия имеют ограничения, связанные с выбором одной из
осей, например, x, и точки С относительно положения точек A и B. Ограничения, накладываемые
M iB 0;
M iB 0;
на выбор оси x (не перпендикулярно AB) и точки C (не лежит на AB), гарантируют, что ни одно
из уравнений не обращается в тождество, при выполнении двух других уравнений.
M iA 0 AB M iA 0 AB
2.5. Теорема Вариньона для произвольной плоской системы сил. Если система сил приводится к равнодействующей, то
момент равнодействующей относительно любого центра равен сумме моментов системы сил относительно того же центра.
Доказательство: Пусть система сил F1, F2, F3 … приводится к равнодействующей R,
линия действия которой проходит через некоторую точку O.
F3
F2
R
x
O
Такая система не находится в равновесии (R ≠ 0). Уравновесим эту систему силой
R’, т.е. приложим в этой точке силу R’, равное по модулю и направленной по линии
действия R в противоположную сторону (R’ = –R) (аксиома о двух силах).,
R
Тогда система сил F1, F2, F3 … и R’ будет находится в равновесии и для нее должна
выполняться условие равновесия, например:
M iA M A (R ) 0
R R
A
Поскольку сила R’, равна равнодействующей R и направлена по линии ее действия в
противоположную сторону, то MA(R’) = –MA(R). Подставляя этого равенства в
предыдущее равенство получим:
M iA M A (R) 0 или M A ( R) M iA
F1
Примеры использования теоремы Вариньона о моменте равнодействующей:
1. Определение момента силы относительно точки, когда сложно вычислять плечо силы. Например:
F2
F
F1
a
A
h
b
Силу F разложим на составляющие F1 и F2. Тогда момент силы F относительно точки
A можно вычислить как сумму моментов каждой из сил относительно этой точки:
M A ( F ) F1b F2 a ( F cos )b (F sin )a
2. Доказательство необходимости ограничений для II и III форм уравнений равновесия:
Если
M 0 , то система приводится к равнодействующей, при этом она проходит через
iA
точку A, т.к. ее момент относительное этой точки должен быть равен нулю (теорема Вариньона).
x
Если при этом M iB 0 , то равнодействующая должна также проходить через точку B.
R
Тогда проекция равнодействующей на ось, перпендикулярную AB, и момент равнодействующей относительно
B 9
С
A
точки, лежащей на AB, будут тождественно равны нулю при любом значении равнодействующей.
16. Глава II. ПЛОСКАЯ СИСТЕМА СИЛ.
ЛЕКЦИЯ 4Плоские фермы.
Методы расчета.
Метод вырезания узлов.
Метод Риттера.
Понятие о линиях влияния
опорных реакций и усилий.
Равновесие сочлененных
тел.
Условие равновесия
рычага.
Условие устойчивости тела
на опрокидывание.
Кинематический способ
определения реакций
(принцип возможных
перемещений).
17.
Лекция 43. Расчет плоских ферм. Фермой называется жесткая конструкция из прямолинейных стержней, соединенных на концах
шарнирами. Если все стержни фермы лежат в одной плоскости, ферму называют плоской.
Узлы фермы – точки, в которых сходятся оси стержней.
d
1
Опорные узлы – узлы, которыми ферма опирается на основание.
5
3
2
4
Верхний и нижний пояса – стержни, образующие верхний и нижний контуры.
Стойки – вертикальные стержни.
h
Раскосы – наклонные стержни.
R
B
RA
Пролет фермы – расстояние между опорными узлами (l).
A
Длина панели – расстояние между стойками (d).
7
6
8
F2
F1
B
F3
Методы расчета. Для расчета усилий, возникающих в стержнях ферм,
l
используются метод вырезания узлов и метод сквозных сечений (метод Риттера).
Основные допущения, принимаемые при расчете ферм:
S A1
1. Все узлы соединения стержней считаются идеальными шарнирами, не
X i 0; S A6 0,
препятствующими взаимному повороту стержней. Узлы в металлических фермах, в которых
S A6 Y 0;
S A1 R A 0.
стержни соединяются при помощи фасонных листов и заклепок, также рассматриваются A
i
RA
как шарнирные, поскольку при нагрузке они допускают малые упругие деформации.
S A6 0,
2. Все внешние нагрузки к ферме прикладываются только в узлах. Для узловой передачи
нагрузки на практике используются специальные балочные конструкции.
S A1 R A
3. Геометрические размеры фермы не изменяются при нагружении (деформации малы).
S12
1
■ 3.1.Метод вырезания узлов. Последовательно вырезаются узлы фермы так, чтобы
X i 0; S12 S16 cos 0,
в двух уравнениях равновесия для каждого из узлов было не более двух неизвестных
Yi 0; S1A S16 sin 0.
усилий. Как правило внешние опорные реакции должны быть предварительно определены.
S
Порядок расчета:
16
S1A
S
S
1. Выбираем в качестве объекта равновесия ферму в целом и определяем опорные реакции:
S16 1 A A1 ,
2. Нумеруем или обозначаем буквами необозначенные узлы. Реакции стержней (или
sin sin
усилия в них) будем обозначать далее двумя индексными цифрами или буквами – первая из
S
них совпадает с номером (обозначением) вырезаемого узла, а вторая указывает к каком узлу
S12 S16 cos A1 cos .
sin
присоединяется другим концом рассматриваемый стержень.
3. Вырезаем узел A (в этом узле всего два неизвестных усилия) и заменяем действие
Далее процесс вырезания узлов и
разрезанных (отброшенных) узлов усилиями (реакциями) SA1 и SA6.
определения усилий повторяется
4. Составляем уравнения равновесия для узла A и вычисляем усилия SA1 и SA6.
в определенном порядке, например:
5. Вырезаем узел 1 (в этом узле всего два неизвестных усилия) и заменяем действие
2, 6, 7, 3, 4, 8, 5.
разрезанных (отброшенных) узлов усилиями (реакциями) S1A, S12 и S16.
Вырезание последнего узла B
6. Составляем уравнения равновесия для узла 1 и вычисляем усилия S12 и S16 (S1A и SA1
может служить для контроля 10
равны алгебраически, поскольку при направлении неизвестных усилий от узла аксиома
правильности расчета.
действия и противодействия выполняется автоматически).
18.
Лекция 4 (продолжение – 4.2)Метод вырезания узлов позволяет сравнительно просто найти усилия в стернях фермы. Недостаткам этого метода является
повторное построении усилий в стержнях, которые один раз проводятся в одном направлении, а другой раз – в противоположном.
Кроме того, последовательное вычисление усилий и подстановка результатов в дальнейший расчет при большом числе узлов чревато
накоплением ошибок, не говоря уже о том, допущенная грубая ошибка в одном из узлов делает дальнейшие вычисления неверными.
■ 3.2. Метод сквозных сечений (метод Риттера). В большинстве случаев не требует для вычисления усилия только в
указанном стержне составления каких-либо других вспомогательных уравнений равновесия кроме того уравнения, в котором
непосредственно участвует искомое усилие. Метод основывается на составлении одного уравнения равновесия с использованием
II и III форм уравнений равновесия произвольной плоской системы сил.
I
Порядок расчета:
d
S 32 3
1
5
2
4
1. Выбираем в качестве объекта равновесия ферму в целом и определяем
опорные реакции:
2. Проводим сквозное сечение, разделяющее ферму на две отдельные части так,
S 36
h
чтобы в сечение попадало не более трех стержней, в одном из которых
RB
S 76
RA
требуется найти усилие, например, сечение I-I для определения S23.
A
6
8
3. Выбирая в качестве объекта равновесия одну часть, например, правую,
7
F2
F1
B
F3
отбрасываем другую (левую) часть.
l
4. Действие отброшенной части на оставшуюся заменяем реакциями стержней,
попавших в разрез – S32, S36 и S76.
I
5. Для искомого усилия S32 находим положение точки Риттера, как точки
M iправ
0; S32h RB 3d F3 2d F2 d 0
пересечения линий действия двух других усилий S36 и S76, не подлежащих
6
определению в данный момент. Точка Риттера для усилия S32 совпадает с узлом 6.
RB 3d F3 2d F2 d
6. Составляем моментное уравнение равновесия для оставленной (правой) части
S32
относительно найденной точки Риттера (узла 6) и определяем искомое усилие.
h
7. Для определения усилия S76 находим положение точки Риттера, как точки пересечения
M iправ
0; S76h RB 2d F3d 0
линий действия двух других усилий S36 и S32, не подлежащих определению в данный момент.
3
Точка Риттера для усилия S76 совпадает с узлом 3.
R 2d F3 d
8. Составляем моментное уравнение равновесия для оставленной (правой) части
S 76 B
относительно найденной точки Риттера (узла 3) и определяем искомое усилие.
h
7. При определении усилия S36 точка Риттера, как точка пересечения линий действия
двух других усилий S76 и S32, не подлежащих определению в данный момент, уходит в
Yi прав 0; S36 sin RB F2 F3 0
бесконечность. В этом случае моментное уравнение равновесия вырождается в
R F2 F3
уравнение равновесия в проекциях на ось, перпендикулярную линиям, уходящим в
S36 B
бесконечность. Этот метод разработан немецким ученым А. Риттером в 1900 г.
sin
Для определения других усилий необходимо провести другое сечение (п.2)
и повторить описанные действия (пп. 3,4,….)
11
19.
Лекция 4 (продолжение – 4.3 – дополнительный материал)■ 3.3. Понятия о линиях влияния опорных реакций и усилий. Железнодорожные (Ж.Д.) мосты, сооружаемые фермами и
балочными конструкциями, при эксплуатации подвергаются подвижной многоосной нагрузке. При движении поезда усилия в
элементах изменяются по некоторому закону и требуется определить наиболее опасные расположения такой нагрузки на сооружении.
Для решения этой задачи используем линии влияния усилий. Линии влияния широко используются в строительной механике.
Линия влияния усилия – график изменения усилия в зависимости от положения единичной подвижной нагрузки.
Выражения для усилий в стержнях фермы от постоянной
R F2 F3
нагрузки содержат величину опорной реакции, например: S 36 B
sin
В случае единичной подвижной нагрузки (F1=F2=F3=0, P=1) соответствующие выражения будут различными
в зависимости от расположения единичной нагрузки:
R 1
R
груз находится слева от сечения I-I:
груз находится справа от сечения I-I S36 B 3
S36 B 3
sin
sin
(на оставленной части фермы):
Таким образом, линия влияния усилия S36 может быть построена с помощью линии влияния опорной реакции RB:
груз находится слева от сечения I-I:
(левая ветвь)
Л.в.S36
Л.в.RB 3
sin
груз находится справа от сечения I-I :
(правая ветвь)
Л.в.S36
Л.в.RB 3 1
sin
Построение линии влияния опорной реакции. Ферму можно в данном случае представить в виде обычной балки:
RA
A
x
l
0
RB
1. Отбрасываем связи и заменяем реакциями:
B RB
2. Составляем моментное уравнение равновесия
и находим величину реакции в функции от
координаты положения груза :
3. Подставляя значения x = 0 и x = l
1
строим график изменения значения
опорной реакции (линию влияния):
P 1
1
M
iA
0;
RBl 1x 0
d
I
2
RB
3
4
x
l
5
h
Построение линии влияния усилия в стержне S36:
1.Построенная
Строим левуюлиния
ветвь л.в.
усилия позволяет
(груз находится
слева)
используя
влияния
легко
найти
величину
соответствующее
выражение
:
усилия от любой статической (постоянной) вертикальной
2. Строим
правую
ветвь л.в.
усилия (груз находится
нагрузки
как сумму
произведений
величинсправа)
сил на значения
используя соответствующее
выражение
:
ординат линии влияния:
3. Строим передаточную прямую, учитывающую узловую передачу нагрузки :
S36 Fi yi F1
d
2d
d
F2
F3
l sin
l sin
l sin
A
6
F1 I
7
l
F2
8
F3
B
d
l sin
1
sin
1
sin
2d
l sin
d
l sin
12
20.
Лекция 4 (продолжение – 4.4)■ 3.4. Равновесие сочлененных тел. Технические конструкции могут состоять из сочлененных между собой тел (балок, ферм).
Количество связей может превышать число независимых уравнений равновесия, которые можно составить для рассматриваемой
конструкции. Такие задачи являются статически неопределимыми. Степень статической неопределимости для плоских систем равна:
n 3 Ж 2 Ш С 3 Д где Д – число жестких дисков, Ж – число жестких заделок, Ш – число неподвижных шарниров,
С – число шарнирных стержней (опорных или соединяющих диски между собой) или подвижных шарниров
В теоретической механике возможно решение только статически определимых задач, в
которых количество связей равно числу независимых уравнений равновесия (n = 0).
RAy
MA
RCy
RCx
R Ax
RCx
С
A
a
F1
RCy
RB
B
b
c
F2
n 3 1 2 1 1 1 3 2 0
1. Выберем в качестве объекта всю конструкцию.
2. Отбросим связи и заменим их действие реакциями.
3. Число неизвестных реакций-4, а число независимых уравнений-3.
Это означает, что необходимо расчленить конструкцию – отбросить
шарнир C и заменить его действие на каждую из частей реакциями.
(CB) :
X
i
0; RCx 0;
RCx , но RCx
RCx ;
4. Число неизвестных реакций – 8, а количество независимых
RCx
M Ci 0; RBb F2 (b c) 0;
уравнений равновесия для обоих частей - 3·2 = 6.
RCy , но RCy
RCy .
RCy
С использованием аксиомы действия и противодействия для каждой
M
0
;
R
b
F
b
0
.
Bi
Cy
2
пары реакций шарнира C общее число неизвестных реакций
уменьшается до 6 и равно общему числу уравнений равновесия:
0;
X i 0; RAx RCx
5. Решение полученной системы уравнений не представляет особых ( AC) :
затруднений в указанном порядке: от вспомогательной балки CB
M Aудерж M Aопрок
Y
0
;
R
R
F
0
;
i
Ay
Cy
1
(не может оставаться в равновесии без балки AC) к основной балке
AC (может находиться в равновесии без балки CB).
F2
(a d ) F1a 0.
M Ai 0; M A RCy
■ Равновесие рычага. Рычаг – твердое тело, имеющее одну
неподвижную точку. Рычаг имеет одну степень кинематической
RAy
подвижности (w = –n = 3Д–3Ж–2Ш–С = 3·1–3·0–2·1–0 =1) и в равновесии может
быть лишь при определенном соотношении активных сил, действующих на рычаг.
F1
F2
b
R Ax
■ Уравнения равновесия рычага (УРР). Применяя общий подход составления
R
F1
Ay
уравнений равновесия к рычагу получаем:
A
Во многих случаях значением опорных реакций не
A
a
b
X i 0; RAx 0;
интересуются и искомое соотношение сил определa R
яют из последнего моментного уравнения, которое
Ax
Yi 0; RAy F1 F2 0; и принимается за уравнение равновесия рычага.
УРР используется при расчете подпорной стенки или груза на опрокидывание:
M Ai 0; F1a F2b 0.
13
Условие устойчивости на опрокидывание: Удерживающий момент относительно неподвижной
точки (от F1) должен быть больше опрокидывающего момента (от F2) относительно этой же точки.
21.
Лекция 4 (продолжение – 4.5 – дополнительный материал)■ 3.5.Кинематический способ определения реакций и усилий. Способ основывается на принципе возможных перемещений:
■ Принцип возможных перемещений – Для равновесия материальной системы, подчиненной стационарным, двухсторонним
и идеальным связям, необходимо и достаточно, чтобы сумма элементарных работ всех активных сил на любом возможном
n
перемещении из предполагаемого положения равновесия равнялось нулю:
Стационарные связи – не зависящие от времени.
A F Fk rk 0.
Двухсторонние связи – препятствующие перемещениям в обоих противоположных направлениях
k 1
(жесткая заделка, шарнир, стержень являются двухсторонними связями, нить, гладкая поверхность-односторонние связи).
Если связь односторонняя, то достаточно просто не рассматривать в качестве возможных перемещений перемещения, соответствующие
тому направлению, в котором связь не может удерживать объект, например, в направлении отрыва объекта от гладкой поверхности.
Идеальные связи – работа которых на любом возможном перемещении равна нулю.
Если связь не идеальная, то реакция такой связи должна быть причислена к действующим (активным) силам, например, сила
трения шероховатой поверхности добавляется к активным силам.
■ Возможные перемещения – бесконечно малые перемещения, допускаемые наложенными на систему связями.
Возможные перемещения не зависят от приложенных к системе сил.
бxA
■ Вычисление возможных перемещений: - в силу малости возможных перемещений при повороте
Заметим, что движущейся не по дуге, а по перпендикуляру
твердого тела любая его точка может рассматриваться
к радиусу вращения в сторону угла поворота:
Для малых
угловMA x 0;
1. для
опорного
момента
A
xнахождения
l
O
A l l cos ;
A
x
cos
≈
1,
sin
≈
,
из уравнений статики потребовалось бы решить как
бyA=бsA
y A три
l sinуравнения
.
y A s A l .
тогда:
минимум
равновесия;
■ Возможная работа силы – элементарная
работа
силы на том
или ином возможном
перемещении:
2. эпюра
возможных
перемещений
пропорциональна
■ Примеры использования принципа возможных перемещений для определения реакций связей: A F s cos( F , r ).
линии влияния усилия;
Пример 1. Определить
Балка неподвижна
и не имеет
возможных, ни действительных перемещений.
3. если задать возможное
перемещение
дляни
искомой
RB
P
реакцию балки в правой опоре: Отбросим связь, реакция которой отыскивается, и заменим ее реакцией:
реакции равным 1, например, б =1, то эпюра
A
B
Без правой опоры балка может поворачиваться под действием активных сил, реакцию RB причисляем
перемещений будет полностью тождественна линии
бsP
к активным силам. Зададим малое возможное перемещение:
б
поскольку
Вычислимвлияния
возможные
перемещения: sP a ; sB l .
бsB
a
Pa Pa
l
Запишем сумму работ: AP R P s R s 0.
R
.
Pa
R
l
0
.
B
A M A 1 1 sPF ( z)B B0; M A s F ( z). B
l
l
Пример 2. Определить опорный момент многопролетной составной балке в левой опоре:
Запишем сумму работ:
Отбросим в жесткой заделке связь, препятствующую повороту балки, и заменим ее парой сил MA:
A M A F sF 0.
MA
Вычислим возможные перемещения:
A
C
B
б
l
бsD
D
P
E
бsP
бsB
b
b
a
l
s B l ; s D s B l ;
s F
a
a
s D
l .
l a
l a
M A F
a
l 0.
l a
M A F
a
l.
l a
14
22. Глава II. ПЛОСКАЯ СИСТЕМА СИЛ.
ЛЕКЦИЯ 5Трение скольжения.
Основные законы.
Способы определения
коэффициента трения.
Угол трения.
Конус трения.
Учет сил трения при
решении задач на
равновесие.
Сопротивление при
качении.
23.
Лекция 5■ 4. ТРЕНИЯ. 4.1. Трение скольжения. Силы трения скольжения возникают между шероховатым телом и шероховатой
поверхностью, если внешних сил не направлена по нормали к поверхности. При действии сдвигающей силы к телу, возникает сила,
противодействующая возможному смещению тела (сила трения сцепления) из равновесного положения.
Основные законы трения (Амонтона - Кулона):
1. Сила трения лежит в касательной плоскости к соприкасающимся поверхностям и направлена в сторону противоположную
направлению, в котором приложенные к телу силы стремятся его сдвинуть или сдвигают в действительности (реактивный характер).
max
2. Сила трения изменяется от нуля до своего максимального значения 0 Fтр Fтр ..
Fтрmax fN.
Максимальная сила трения пропорциональна коэффициенту трения и силе нормального давления
.
3. Коэффициент трения есть величина постоянная для данного вида и состояния соприкасающихся поверхностей (f = const).
4. Сила трения в широких пределах не зависит от площади соприкасающихся поверхностей.
■ Способы определения коэффициента трения.
1. Сдвигающая (внешняя) сила изменяется от нуля до своего максимального значения – 0 ≤ T ≤ Tmax, (0 ≤ P ≤ Pmax).
2. Сила нормального давления изменяется от некоторого начального значения до минимального значения – N0 ≥ N ≥ Nmin (G0 ≥ G ≥ Gmin).
Fтрmax
G
T max
X i 0;
Yi 0;
T max Fтрmax 0;
N G 0.
T max fN ;
N
N G;
P max
f
T max P max
.
N
G
Fтрmax
X 0;
Y 0;
i
G min T
i
N
T Fтрmax 0;
N min G min 0.
T fN min ;
min
P
N min G min ;
T
P
f min min .
N
G
3. Сдвигающая сила и сила нормального давления изменяются при изменении угла наклона плоскости скольжения от нуля до
Активные силы (G, T и др.) можно заменить
максимального значения – 0 ≥ φ ≥ φmax .
■ Угол трения. С учетом силы трения, возникающей при контакте с
равнодействующей силой P, имеющей
max уголmax
X i α.
0; Можно
G sinпоказать,
Fтрчто 0; шероховатой поверхностью полная реакция такой поверхности может
отклонения
от вертикали
рассматриваться как геометрическая сумма нормальной реакции
Fтрmax
maxкогда эта
равновесие
возможно
лишь
в
том
случае,
G
Yi 0;
N G cos 0. абсолютно гладкой поверхности и силы трения:
сила остается внутри пространства конуса трения:
Угол отклонения полной реакции
max
max
max
N
R
N
F
max
тр
шероховатой поверхности – угол
N
G sin
fN ;
R
max.
трения, равный:
Условие равновесия по оси x: Psinα
≤
F
тр
N G cos max ;
max
T
Из уравнения равновесия по оси у: N = Pcosα.
Fтрmax
Fтр
max
max
max
arctg ( f )
Максимальная сила трения
= fN
= tgφN
=
G sinF тр
G sin
arctg
max
f
tg
.
N
tgφPcosα.
N
G cos max
G
Тогда Psinα ≤ tgφPcosα, (Psinα/Pcosα=Pcosα) откуда
15
tgα ≤ tgφ и α ≤ φ.При изменении направления сдвигающей силы T на опорной поверхности ее поворотом относительно
нормали к плоскости полная максимальная реакция шероховатой поверхности описывает конус трения.
24.
Лекция 5 (продолжение – 5.2)■ 4.1.1. Учет сил трения при решении задач на равновесие. При наличии сил трения:
К действующим на объект активным силам и реакциям абсолютно гладких поверхностей добавляются соответствующие
силы трения, направленные по общей касательной к контактным поверхностям в сторону, противоположную возможному
смещению точки касания объекта относительно опорной шероховатой плоскости.
2.
К уравнениям равновесия, составленным для объекта, добавляются выражения для максимальных сил трения в
количестве, равном числу сил трения.
■ Пример решения задачи на равновесие с учетом трения. Человек весом G собирается установить легкую лестницу под углом α
к вертикали (стене) и взобраться на половину длины лестницы для выполнения работы. Коэффициенты трения в точках
контакта лестницы с полом (A) и со стеной (B) равны fA и fB соответственно. Определить предельное значение угла наклона,
при котором лестница с человеком может сохранять равновесие. Весом лестницы пренебречь.
B
1. Выделим объект (человек и лестница), отбрасываем связи и заменяем их действие реакциями поверхности.
Fтр
NB
2. Добавляем активные силы (силу тяжести G).
3. Добавляем силы трения, направленные в сторону, противоположную возможному перемещению контактных
B
точек A и B лестницы под действием приложенной активной силы.
A
1.
G
FтрA
NA
4. Составляем
уравнения
равновесия:
A
6. Подстановка последних выражений
в уравнения равновесия с простыми
преобразованиями третьего уравнения
(разделим оба части на АВcosα) дает:
X i 0;
Yi 0;
N B FтрA 0;
FтрB
M iA 0; G
G N A 0;
AB
sin FтрB AB sin N B AB cos 0.
2
N B f A N A 0;
7. Решение первых двух
X i 0;
Yi 0; f B N B G N A 0;
1
2
M iA 0; G tg f B N B tg N B 0.
Fтр f A N A ;
5. Добавляем
выражения
для сил трения:
уравнений дает выражения
для нормальных реакций:
FтрB f B N B ;
NA
G
;
1 f A fB
NB
f AG
.
1 f A fB
tg
8. Подстановка выражений для нормальных реакций в третье уравнение равновесия приводит к возможности
определения предельного угла наклона α:
■ Определение области равновесия. Задача решена для конкретного положения
RB
человека, угол наклона соответствует предельному равновесию (использованы
B
максимальные значения сил трения). С помощью понятия конуса трения, образовываемого
B
B
полной реакцией шероховатой поверхности и теоремы о трех силах можно определить
область возможных равновесных положений человека на лестнице.
G
A
A
Для этого достаточно по заданным коэффициентам трения определить углы трения,
определяющие предельные положения полной реакции и построить конусы трения. Общая
RA
область конусов дает область равновесных положений человека. Хорошо видно, что для
A
более высокого положения человека надо уменьшать угол наклона.
2 fA
1 f A f
B
16
25.
Лекция 5 (продолжение 5.3)■ 4.2. Трение качения. Трением качения называется сопротивление, возникающее при качении одного тела по поверхности
другого. Трение качения возникает из-за деформации катка и плоскости, если приложить к оси катка силу Р, стремящуюся его
двигать по плоскости. Рассмотрим случай, когда сила Р параллельна горизонтальный плоскости. Возникновение пары сил,
препятствующей качению, связана с деформацией опорной плоскости, в результате которой равнодействующая нормальных
реактивных сил по площадке контакта смещена от линии действия силы тяжести в сторону возможного или действительного
движения на некоторое расстояние fк. (рис.).
Одна пара сил (P и F) с моментом Р ∙r (r - радиус катка) и вторая пара сил (N и G ) с моментом N ∙fк,
fк
удерживающая каток в равновесии.
P
G
Fтр
N
Основные законы трения качения:
1. Момент трения качению всегда направлен в сторону противоположную, тому направлению, в котором
приложенные к телу силы стремятся его повернуть, или действительному повороту под действием этих
сил (реактивный характер).
max
2. Момент трения качению изменяется от нуля до своего максимального значения: 0 M к M к .
Максимальный момент трения качению пропорционален коэффициенту трения
качения и силе нормального давления:
.
M кmax f к N
3. Коэффициент трения качения есть величина постоянная для данного вида и
состояния соприкасающихся поверхностей (fк = const).
4. Момент сопротивления качению в широких пределах не зависит от радиуса катка.
Если коэффициент трения скольжения является безразмерной величиной, то коэффициент трения качения измеряется
единицами длины (мм., см., м.) и равен по величине указанному смещению равнодействующей нормального давления. В силу
малости деформаций коэффициент трения качения имеет очень малую величину и составляет, например, для стального
бандажа по стальному рельсу 0.005 см., дерево по дерево 0,05 - 0,08 см., сталь закаленная по стали (шариковой подшипник)
0,001см. При действии силы Р интенсивность давления у края катка вдоль направлении Р возрастает, а у противоположного края
убывает. С увеличением Р это смещение растет, и следовательно fк – растет. При Р < Рпр, каток находится в покое; при Р > Рпр
каток начинается качение.
17
26. Глава III. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
ЛЕКЦИЯ 6Произвольная
пространственная система
сил.
Моменты силы
относительно центра и оси.
Связь момента силы
относительно точки и
момента силы
относительно оси.
Теоремы о парах.
Сложение произвольно
расположенных сил в
пространстве.
Главный вектор и главный
момент.
27.
Лекция 6Глава II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ.
5. Произвольная пространственная система сил. Силы не лежат в одной плоскости и их линии действия не
пересекаются в одной точке. Для рассмотрения такой системы сил необходимо ввести новые понятия:
1. Момент силы относительно центра в пространстве.
2. Момент силы относительно оси.
3. Момент пары сил в пространстве.
1. Момент силы относительно центра (точки) в пространстве – векторная величина, равная векторному
M O (F ) r F
произведению радиуса-вектора, проведенного из центра к точке приложения силы, и вектора силы.
По определению векторного произведения вектор момента силы направлен перпендикулярно плоскости, проведенной через
центр и силу, в ту сторону, откуда поворот радиуса-вектора к вектору силы на наименьший угол представляется происходящим по
часовой стрелке.
M O (F )
Модуль вектора момента силы относительно центра равен: M O ( F ) Fr sin( r , F ) Fh
A
Модуль вектора момента силы относительно центра численно равен удвоенной
r
площади треугольника OAB.
O
2. Момент силы относительно оси – скалярная величина, равная
F h
B
произведению проекции вектора силы на плоскость, перпендикулярную оси, на
плечо этой проекции относительно точки пересечения оси с плоскостью, взятая
z
со знаком + (плюс), если вращение плоскости под действием силы
F
представляется при взгляде навстречу оси происходящим против
часовой стрелки, и со знаком – (минус) в противном случае.
M z ( F ) F1h1
M z (F )
Момент силы относительно оси численно равен удвоенной
a
площади треугольника Oab.
Связь момента силы относительно центра и относительно оси.
O
h1
F
1
Модуль вектора момента силы относительно центра, лежащего на оси z, равен
b
удвоенной площади треугольника OAB:
M O ( F ) Fh 2S OAB
Момент силы относительно оси z, равен удвоенной площади треугольника Oab:
M z ( F ) F1h1 2S Oab
A
z
F
h
B
a
Треугольник Oab получен проекцией треугольника OAB на плоскость,
перпендикулярную оси z, и его площадь связана с площадью треугольника OAB
соотношением:
- двугранный угол между плоскостями
F h1
S Oab S OAB cos
треугольников.
b
Поскольку вектор момента силы относительно точки перпендикулярен
плоскости треугольника OAB, то угол между вектором и осью равен углу .
Таким образом, момент силы относительно оси есть проекция
M z ( F ) M 0 ( F ) cos
вектора момента силы относительно центра на эту ось:
M z (F )
M O (F )
O
18
28.
Лекция 6 (продолжение – 6.2)3. Момент пары сил в пространстве – вектор, перпендикулярный плоскости действия пары, направленный в
ту сторону, откуда вращение плоскости под действием пары представляется происходящим против часовой стрелки.
Модуль вектора момента пары равен произведению одной из сил пары на плечо пары:
F
M Fd F d
5.1. Теоремы о парах (Теоремы приводятся без доказательств).
О переносе пары сил в плоскость, параллельную плоскости ее действия – Пару сил можно перенести
в любую плоскость, параллельную плоскости ее действия. Кинематическое состояние тела не изменится.
Об эквивалентности пар сил – Пару сил можно заменить другой парой сил, если их моменты геометрически
(векторно) равны. Кинематическое состояние тела не изменится.
О сложении пар сил на плоскости – Систему пар сил на плоскости можно заменить одной парой, момент которой
равен геометрической (векторной) сумме моментов исходных пар. Кинематическое состояние тела не изменится.
Условие равновесия системы пар сил: M M 0
M ( F , F )
d
F
i
Далее будем по-прежнему придерживаться общего плана исследования системы сил, последовательно решая три
вопроса:
1. Как упростить систему?
2. Каков простейший вид системы?
3. Каковы условия равновесия системы?
5.2. Приведение плоской произвольной системы сил к заданному центру. Выбираем произвольную точку на плоскости
и каждую из сил переносим по методу Пуансо в эту точку. Вместо исходной произвольной системы получим сходящуюся систему
сил и систему пар.
В отличие от ранее рассмотренной плоской произвольной системы сил теперь при использовании метода Пуансо
присоединенные пары сил характеризуются
векторами.
Сходящаяся
система сил приводится к одной силе, приложенной в центре приведения.
F2
В общем
случаепар),
плоская
произвольная
Система пар приводится к одной паре (теорема
о сложении
момент
которой равен
система
сил
приводится
к
одной силе,
векторной сумме моментов исходных сил относительно центра приведения.
называемой главным вектором и к паре с
F1
моментом, равным главному моменту всех
h h2
MO
F3 1
F3
сил системы относительно центра
*
h3
R
приведения:
F
F2
F1
1
F2
A
F3
R * Fi - главный вектор,
A
M M A M iA - главный момент.
19
29. Глава III. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
Лекция 7Аналитическое
определение главного
вектора и главного
момента.
Уравнения равновесия
произвольной
пространственной системы
сил.
Возможные случаи
приведения системы.
Зависимость главного
момента от выбора центра
приведения.
Инварианты системы.
Теоремы Вариньона.
30.
Лекция 75.3. Аналитическое определение главного вектора системы – вычисляется так же, как и ранее равнодействующая, через проекции
на координатные оси и единичные векторы (орты):
*
R Fi F1 F2 .... X 1i Y1 j Z1k X 2i Y2 j Z 2 k ...
R * ( X 1 X 2 ...)i (Y1 Y2 ...) j (Z1 Z 2 ...)k Rx*i R *y j Rz* k
R*
R x* X i ; Направляющие
Отсюда
cos( R * , x) x* ; Модуль
проекции
R
*
косинусы
главного вектора:
главного вектора: R y Yi ; главного вектора:
*
Ry
cos( R * , y )
R z* Z i ;
R*
R * Rx*2 R *y2 Rz*2
.
5.4. Аналитическое определение главного момента системы – вычисляется аналогично через проекции на координатные оси
и единичные векторы (орты):
M A M i M1 M 2 .... M1x i M1y j M1z k M 2 x i M 2 y j M 2 z k ...
M A (M1x M 2 x ...)i (M1y M 2 y ...) j (M1z M 2 z ...)k M x i M y j M z k
M x M ix ;
M y M iy ;
Mx
cos( M
;
A , x ) к равнодействующей:
Условие
приведения
системы
MA
Направляющие
Модуль
* главного момента:
MA
косинусы R * M R * M cos(
R
,
M A) 0
M
A
A
y
M A , y)
.
M z M iz ; главного момента :cos(
MA
*
M A 0; R M A 0
Условием равновесия пространственной
произвольной системы сил является
R * Fi 0
*и главного момента* системы в ноль:
*
одновременное обращение главного вектора
R M ; R M 0 (cos( R , M ) 0)
Отсюда
проекции
главного момента:
A
A
A
5.5. Уравнения равновесия. УР получаются
в виде системы шести
уравненийформе:
из условий равновесия с
В аналитической
(координатной)
использованием выражений для проекций главного* вектора и главного
момента
системы
сил:
*
*
*
R M A Rx M x R y M y Rz M z 0
Возможные случаи
приведения
пространственной
произвольной
системы сил:
R*
1
2
3
4
MA
R* 0 M A 0
R* 0 M A 0
R* 0 M A 0
R* 0 M A 0
Дополнительное
условие
Простейший вид
системы
M x2 M y2 M z2
M M A M iA 0
X i 0;
Yi 0;
Z i 0;
M xi 0;
M уi 0;
M zi 0.
Равнодействующая
R MA
R* M A
*
Пара сил
Равнодействующая
R R *
R*
Условия равновесия
MA
d
d
A
B
R R *
MA
R*
20
31.
Лекция 7 (продолжение – 7.2)5.6. Зависимость главного момента системы от выбора центра приведения – рассмотрим как изменяется момент
произвольной силы Fi при переходе от одного центра приведения к другому и запишем выражения для моментов силы относительно
каждого из центров:
M (F ) r F M (F ) r F
A
Fi
i
Ai
i
B
i
Bi
i
1. Свяжем между собой точки приведения A и B радиус-вектором d:
rAi
rBi
d
d rAi rBi
2. Подставим радиус-вектор rBi в формуле для момента силы MB(Fi): M B ( Fi ) (rAi d ) Fi rAi Fi d Fi
3. Просуммируем моменты всех сил MB(Fi): M B ( Fi ) rAi Fi d Fi M A ( Fi ) d Fi
B 4. Получили зависимость главного момента сил от выбора центра приведения:
A
или rBi rAi d
MB M A d R*
Рассмотрим более подробно приведение системы сил к простейшему виду с использованием этой зависимости. Пусть
система привелась в точке A к главному вектору R* и паре с главным моментом MA, имеющих между собой произвольный угол α.
R1 * R *
R*
MA
1. Разложим главный момент пары MA на два момента M* и M1, по двум
направлениям: направлению главного вектора и перпендикулярно ему.
2. Представим пару сил с моментом M1, в виде сил, равных
по модулю главному вектору. Плечо этой пары будет равно:
M*
d
3. Систему сил в точке A удалим (аксиома присоединения).
A
d
O
M1
R*
4. Оставшуюся пару сил с моментом M* перенесем в точку приложения
оставшейся силы R’* (теорема о переносе пары в пространстве).
Т.о.,M
исходная
система сил в центре приведения A в новом центре приведения O превратилась в силовой (статический) винт и
1
более не может быть упрощена. Перпендикулярная главному вектору составляющая главного момента M1 исчезла, а другая
составляющая M*
R1*осталась
R * неизменной. Заметим, исходная величина главного момента равна:
*2
2
*2
M A M M 1 M (R*d ) 2
При выборе
точек
по линии
AO от исходной
точки дочасти
конечной
d → 0 и главный
момент
MA → M* = min, минимальному
Умножая
наприведения
модуль главного
вектора
левую и правую
выражения
главного
минимального
главному
моменту.
Геометрическое
место точек
приведения, для которых главный момент системы является
момента
в проекции
на центральную
осьцентров
получаем:
минимальным называется центральной осью системы.
R * M * R,* M A cos( M A , R * ) R * M A
откуда главный
минимальный
момент выражается
скалярное
Кинематическое
состояние
системы не меняется
при переносечерез
главного
векторапроизведение:
и главного момента вдоль
* центральной оси
R M
*
A
системы. Следовательно, полученный результат справедлив для любой точки приведения, лежащей на
показать,
Mэтой
оси. *Можно
что при выборе точек приведения на одном и том же расстоянии от центральной оси (цилиндрической поверхности)
главные
R
моменты системы равны по модулю и образуют одинаковый угол α с образующей цилиндра:
*
*
Главный минимальный момент может быть вычислен как проекция главного момента
в любой точке приведения на центральную ось:
*
*
M M A cos M A cos( M A , R )
cos
M
MA
M
M *2 ( R * d ) 2
21
32.
Лекция 7 (продолжение – 7.3)5.7. Инварианты системы сил – величины, не зависящие от выбора центра приведения.
Первый (векторный) инвариант – главный вектор системы сил R*:
R * Fi
Главный момент не является инвариантом, поскольку он зависит от выбора центра приведения. Однако существует
величина, связанная с главным вектором, не зависящая от выбора центра приведения:
MB M A d R*
1. Запишем зависимость для главного момента системы от выбора точки приведения:
2. Умножим левую и правую части этого выражения скалярно на главный вектор и раскроем скобки:
R * M B R * ( M A d R * ) R * M A R * (d R * )
3. Второе слагаемое в правой части обращается в ноль, т.к. главный вектор R* перпендикулярен вектору векторного
произведения в скобках. Отсюда получаем тождество:
*
*
Т. о., скалярное произведение главного вектора R* на вектор
главного момента MA есть второй (скалярный) инвариант:
R MB R MA
R * M A in var
Отсюда, главный минимальный момент M* также является инвариантной величиной:
M
*
R* M A
R*
in var
in var
in var
5.8. Теоремы Вариньона о моментах равнодействующей для пространственной системы сил.
Если система сил имеет равнодействующую, то момент равнодействующей относительно любого центра равен
геометрической сумме моментов сил системы относительно того же центра.
Момент равнодействующей относительно любой оси равен алгебраической сумме моментов сил системы относительно той
же оси. (Так как «теорема Вариньона о моментов равнодействующей» справедлива и для моментов относительно любой оси).
Доказательство: Пусть система сил F1, F2, F3 … приводится к равнодействующей,
F3
F2
приложенной в точке O. Такая система не находится в равновесии (R ≠ 0).
Уравновесим эту систему силой R’, равной равнодействующей R, направленной по
линии ее действия в противоположную сторону (аксиома о двух силах).
Система исходных сил F1, F2, F3 … и уравновешивающей силы R’ находится в равновесии
R
и должна удовлетворять условиям равновесия, например:
O
M iA M A (R ) 0
R
A
F1
R R
Поскольку сила R’, равна равнодействующей R и направлена по линии ее действия
в противоположную сторону, то MA(R’) = - MA(R). Подстановка этого равенства в
уравнение равновесия дает:
или
M iA M A (R ) 0
Cпроектируем это векторное равенство на любую ось, например, x:
M A ( R ) M iA
M x ( R ) M ix
22
33. Глава IV. ЦЕНТР ТЯЖЕСТИ
Лекция 8Сложение параллельных
сил.
Центр параллельных
сил.
Центр тяжести.
Определение положения
центра тяжести
однородных тел.
Центры тяжести
простейших фигур.
Способы определения
положения центров
тяжести.
34.
Лекция 8Глава IV. ЦЕНТР ТЯЖЕСТИ.
6.1. Сложение параллельных сил. Основной результат – две параллельные и направленные в одну сторону силы приводятся к
одной силе – равнодействующей, приложенной в точке, делящей прямую на расстояния, обратно пропорциональные величинам сил.
Последовательно складывая попарно параллельные силы приходим также к одной силе – равнодействующей R:
R Fi
Если все силы повернуть на один и тот же угол и вновь провести сложение сил, то получаем другое направление
приложения равнодействующей, не изменяющей своего положения при одновременном повороте всех сил на один и тот же угол.
Такая точка (С) называется центром параллельных сил (цпс.). Понятие цпс используется при определении положений центров
тяжести тел.
6.1.1. Центр параллельных сил. Точка С, не изменяющей своего положения при одновременном повороте всех сил на один и тот же угол называется центром параллельных сил.
Рассмотрим три параллельные силы, приложенные к телу в разных точках.
Положение центра параллельных сил (С) найдем с помощью теоремы Вариньона:
С
r2
F2
M A ( R ) M iA или rC R r.i Fi
F
F2
F1 1
r1
Каждую из сил представим с помощью единичного вектора e, параллельному линиям действия
rC
R
R
сил:
Fi Fi e и R Fi Fi e
r3
.
F3
r
(
Fi e )центра
ri тяжести
Fi e илиможно
С учетом
принятых
гипотез
при
определении
положения
C
F3
Тогда предыдущее равенство примет вид:
после
A
использовать
формулы
для
определения
положения
центра
параллельных
перестановки скалярных множителей в векторных произведениях: (r F ) eсил:
( F r ) e
C
i
i i
Gi zi - где G – силы тяжести элементарных
иGидентичности
G yi ; z
i xi
xC
; yC второгоi сомножителя
Из равенства векторных произведений
следует:
Fi ri
r Fi Fi ri , откуда
C
rC
Gi
Gi
Gi C объемов.
Fi
Проекции полученного соотношения для радиуса-вектора центра параллельных сил на координатные оси дают аналитические
формулы для определения координат центра параллельных сил:
Fx
Fy
Fz
xC
i i; y i i; z i i
C
C
Fi
Fi
Fi
6.2. Центр тяжести. Центр тяжести тела называется центр системы параллельных сил (С), которую образуют силы тяжести
его элементарных частиц. При определении положения центра тяжести тела используются гипотезы:
1. Линии действия сил тяготения, приложенные к отдельным частицам тела, параллельны (рассматриваемые тела имеют
размеры много меньшие радиуса Земли и углом между линиями действия сил тяготения частиц тел можно пренебречь);
2. Ускорение свободного падения g = const (высота рассматриваемых тел много меньше радиуса Земли и изменением
23
величины ускорения свободного падения по высоте тела можно пренебречь)
3. Рассматриваемые тела – однородные (нет включений материалов с другой плотностью) и сплошные (нет пустот).
35.
Лекция 8 (продолжение – 8.2)6.2.1. Определение положения центра тяжести однородных тел. Выделим элементарный объем dV = dxdydz.
Сила тяжести такого объема равна dG = dV, где =const - объемный вес. Замена суммирования дискретных сил тяжести Gi
непрерывным распределением приводит к интегральным выражениям по объему тела для определения координат центров
тяжести, например, координаты xC:
xdV
zdV
ydV
Для всех трех
V
xdG
xdV
xc
координат получаются
zc V
yc V
x
dxdydz
dV
подобные
выражения:
dV
dV
G
V
xc
dG
dxdydz
dV
G
xHdxdy
Hdxdy
dS
xdS
В частном случае плоского тела (постоянной
толщины H =const ), dV = Hdxdy = HdS:
xc
S
xc
V
V
xdS
ydS
S
Для линейного тела (постоянного поперечного сечения
S = const, ось – плоская кривая), dV = SdL:
Прямоугольник: dS=bdy
y
dy
h
y
yc
ydS
S
dS
S
L
h
h
0
0
ybdy b ydy
bdy b dy
h
h
0
0
b
y
2
bh
0
h
2
R
Треугольник:
y
by
b
h y
;
h
by
h y
b;
h
dS by dy
xc
dS
x
h y
bdy
h
xc
xdS
b
dS
S
xdL
yc
L
dL
ydL
L
dL
L
1
1
R( Rd ) R 2 d
2
2
S
dS
S
2 0
2
R2
R cos
d
3
2
2
R
2 0
d
2
b y 2 y3
h
h
y
b
bh 2
h
2
ydS
y
bdy
(
hy
y
)
dy
h 2
3 0
0 h
h
h 0
6 h
S
y
y
c
h
S dS 0h h y bdy b 0h (h y)dy b hy y 2 1 bh 3
h
h
2
h
2 0
x
h
S
x
h
dy
dS
L
Круговой сектор:
d
x
b
xSdL
SdL
dL
L
2 h
yc
S
S
xdL
x
6.2.2. Определение положения центра тяжести простейших плоских тел: c
V
V
2 3
R sin
3
0
R 2
2 R sin
3
0
24
36.
Лекция 8 (продолжение – 8.3)6.3. Методы определения положения центра тяжести сложных фигур.
1. Метод разбиения – сложная фигура разбивается на совокупность простых фигур, для которых известны положения
центра тяжести или легко определяются:
2. Метод отрицательных площадей – так же, как и в методе разбиения,
y
xi S i x1 S1 x2 S 2 сложная фигура разбивается на совокупность простых фигур, для которых
xC
1
известны положения центра тяжести или легко определяются, но при
S1 S 2
Si
наличии отверстий или пустот удобно их представление в виде
2
y
«отрицательных» областей. Например, следующая фигура вместо разбиения
2
на 4 обычных прямоугольника, может быть представлена как совокупность
x
двух прямоугольников, один из которых
1
xi S i x1S1 x2 ( S 2 )
x1
имеет отрицательную площадь:
x2
x
x
x1
x2
C
S
i
S1 ( S 2 )
Замечание. Поскольку координата, например, x2 , может быть отрицательна,
то не следует представлять это выражение с использованием разностей:
x1 S1оси
xили
3. Метод симметрии – при наличии у фигуры оси или плоскости симметрии центр тяжести лежит на этой
2 S 2в этой
x
C
плоскости. С учетом этого свойства уменьшается количество координат центра тяжести, подлежащих определению.
S1 S 2 См.,
например, определение положения центра тяжести кругового сектора.
4. Метод интегрирования – при наличии у фигуры достаточно простого контура, описываемым известным уравнением
(окружность, парабола и т.п.), выбирается элементарная площадка или полоска и выполняется аналитическое
интегрирование. См. например, определение положения центра тяжести треугольника или кругового сектора. При более
сложном контуре, который может быть разбит на более простые граничные отрезки используется предварительно метод
разбиения. При сложностях с аналитическим интегрированием используются численные методы интегрирования.
5. Метод подвешивания – экспериментальный метод, основанный на том, что при подвешивании тела или фигуры за какую-либо
произвольную точку центр тяжести находится на одной вертикали с точкой подвеса. Для определения положения центра тяжести
плоской фигуры достаточно ее подвесить поочередно за две любые точки и прочертить соответствующие вертикали, например, с
помощью отвеса, и точка пересечений этих прямых соответствует положению центра тяжести фигуры.
25




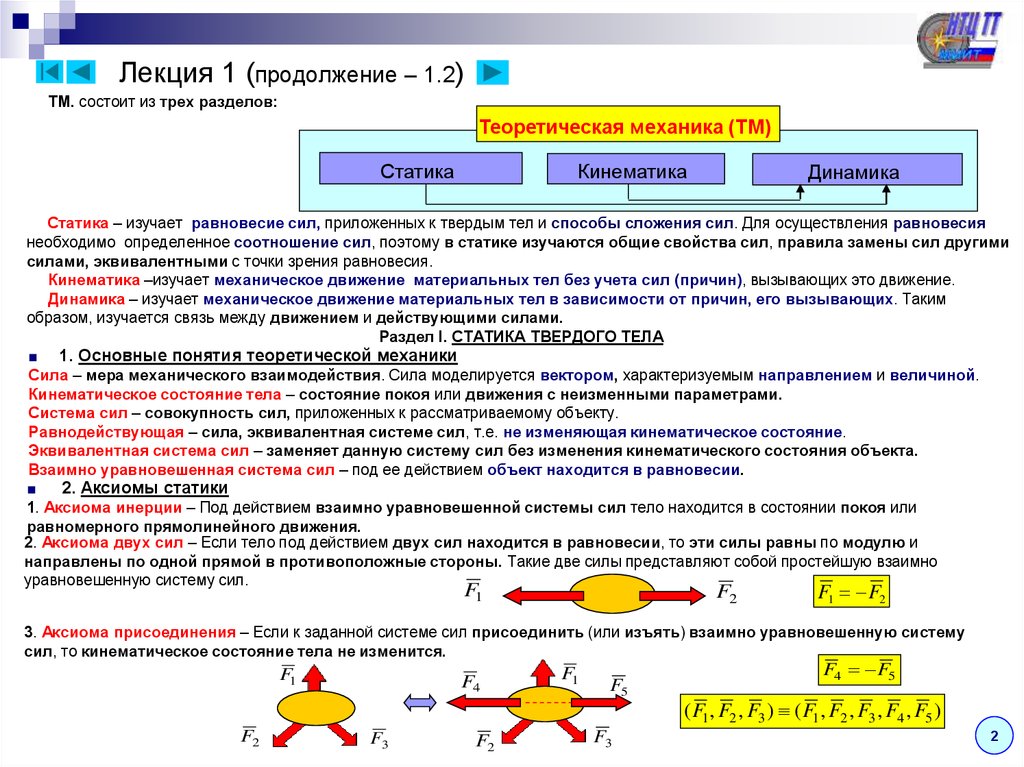

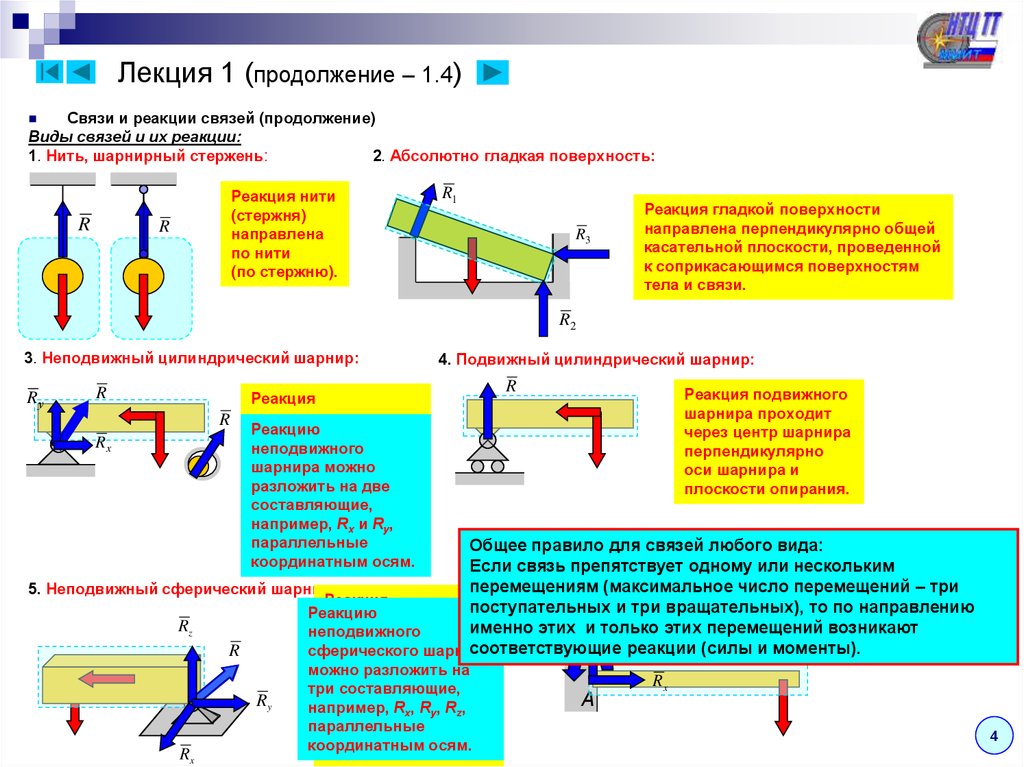

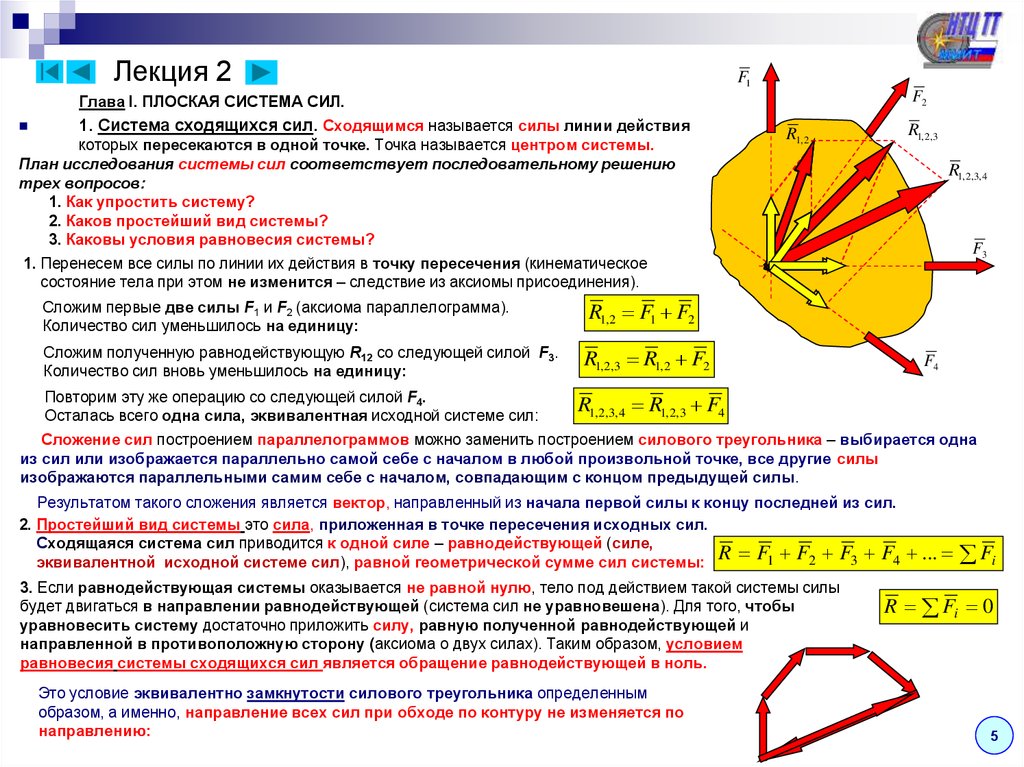















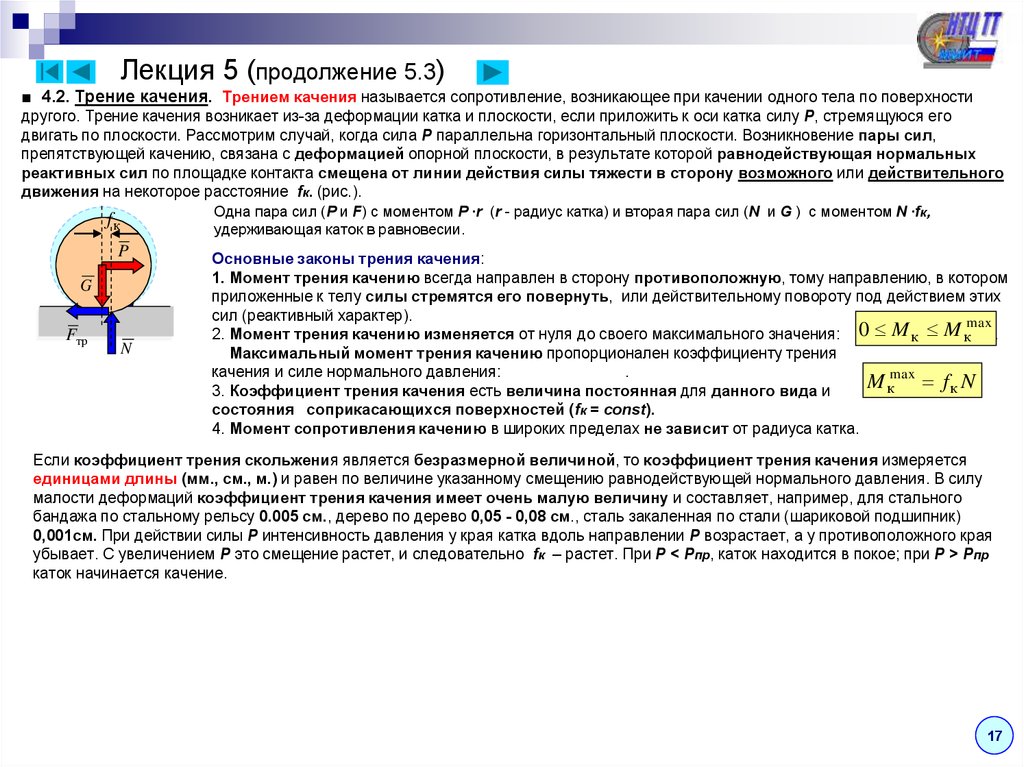










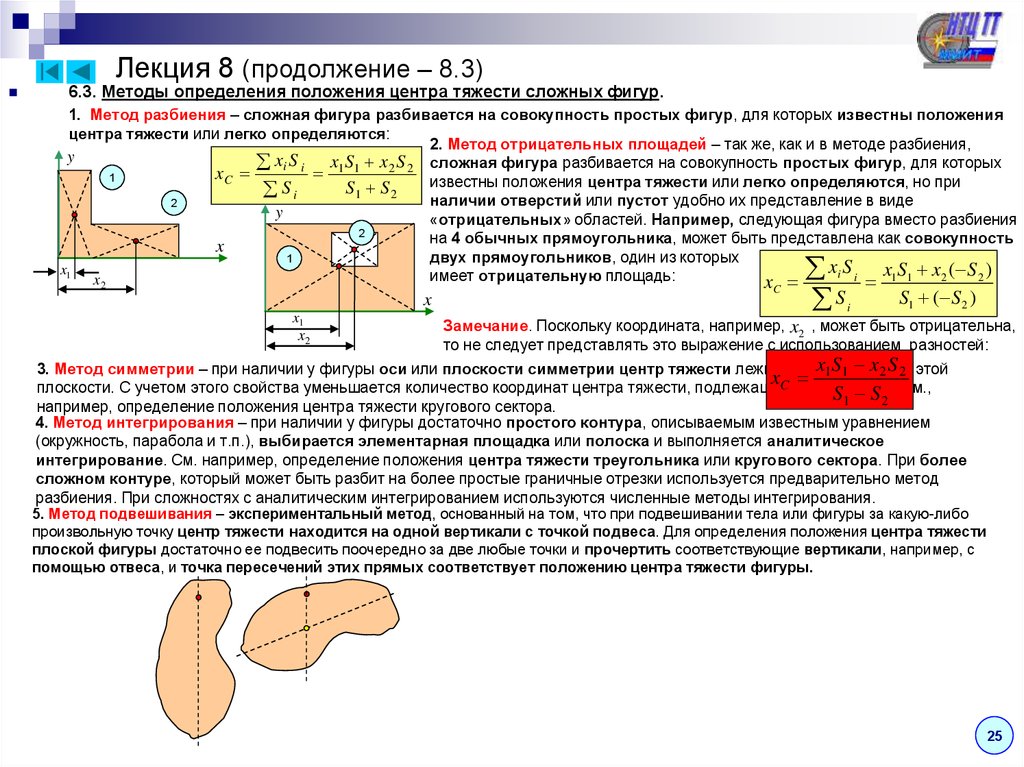
 physics
physics








