Статика

1.

СТАТИКА

2. Основные понятия

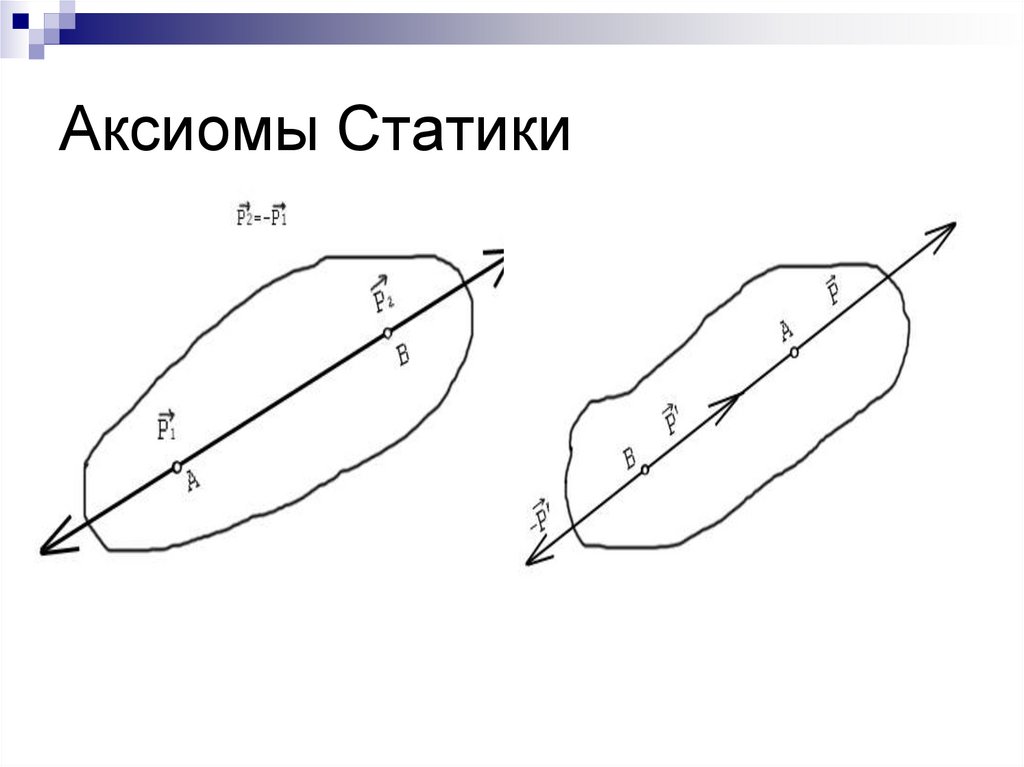
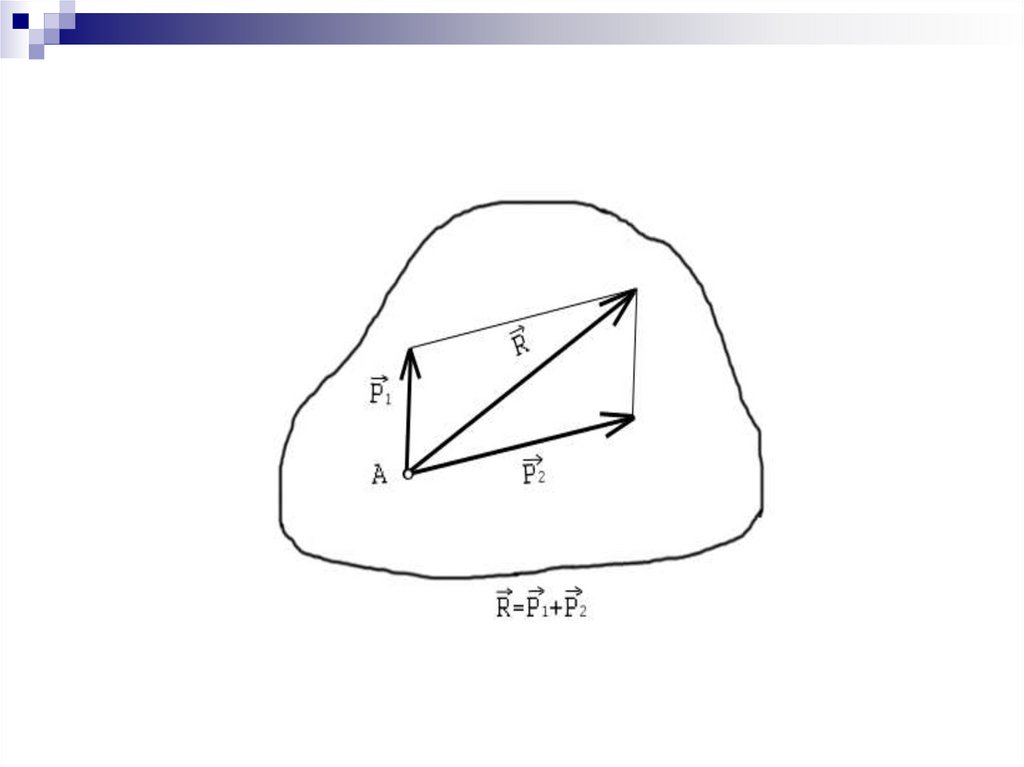
3. Аксиомы Статики

4.

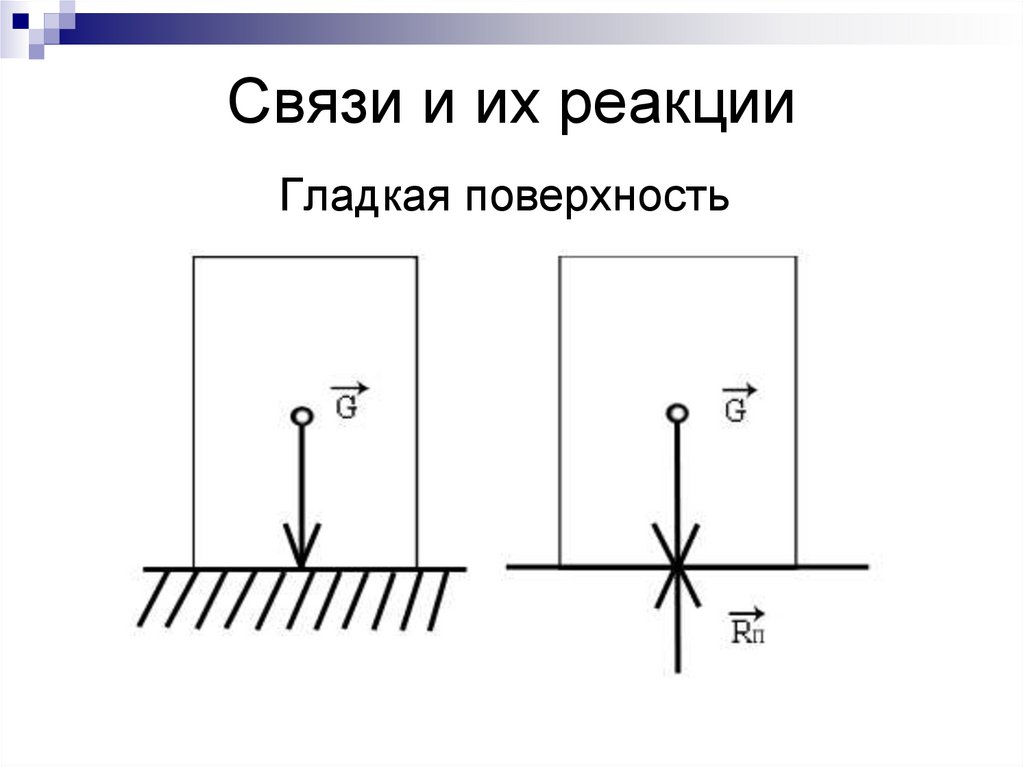
5. Связи и их реакции

Гладкая поверхность

6.

Гладкая поверхность

7.

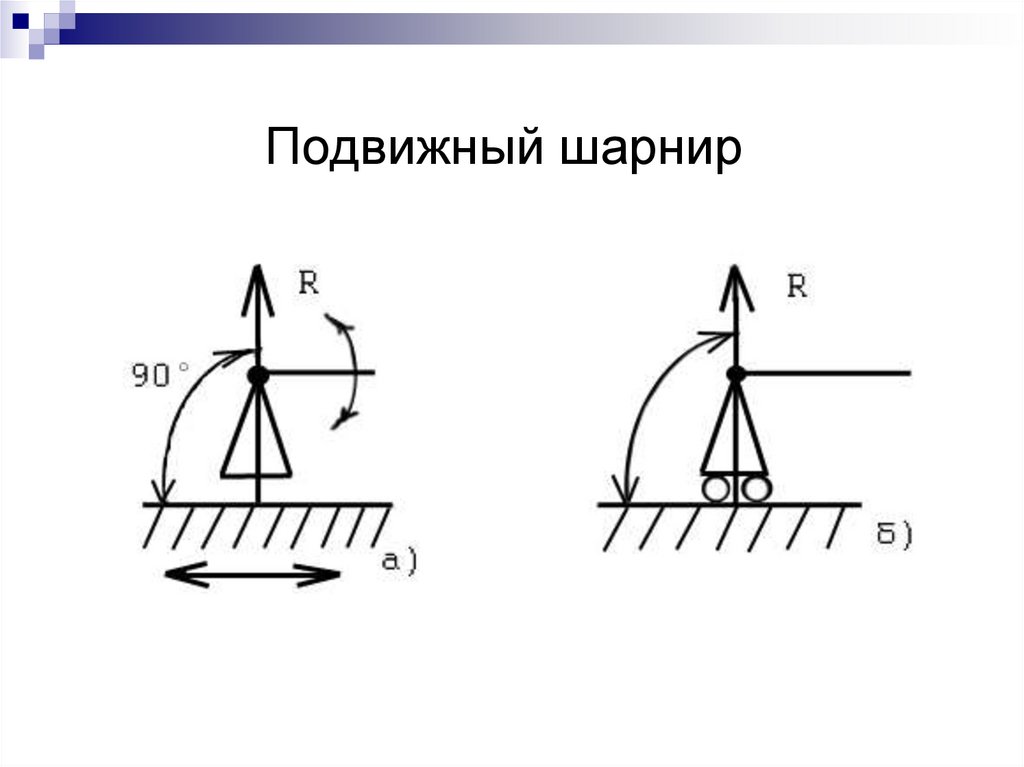
Гибкая связь

8. Подвижный шарнир

9. Неподвижный шарнир

10. Примеры шарниров

11. Защемление или «заделка»

Ry
Rx

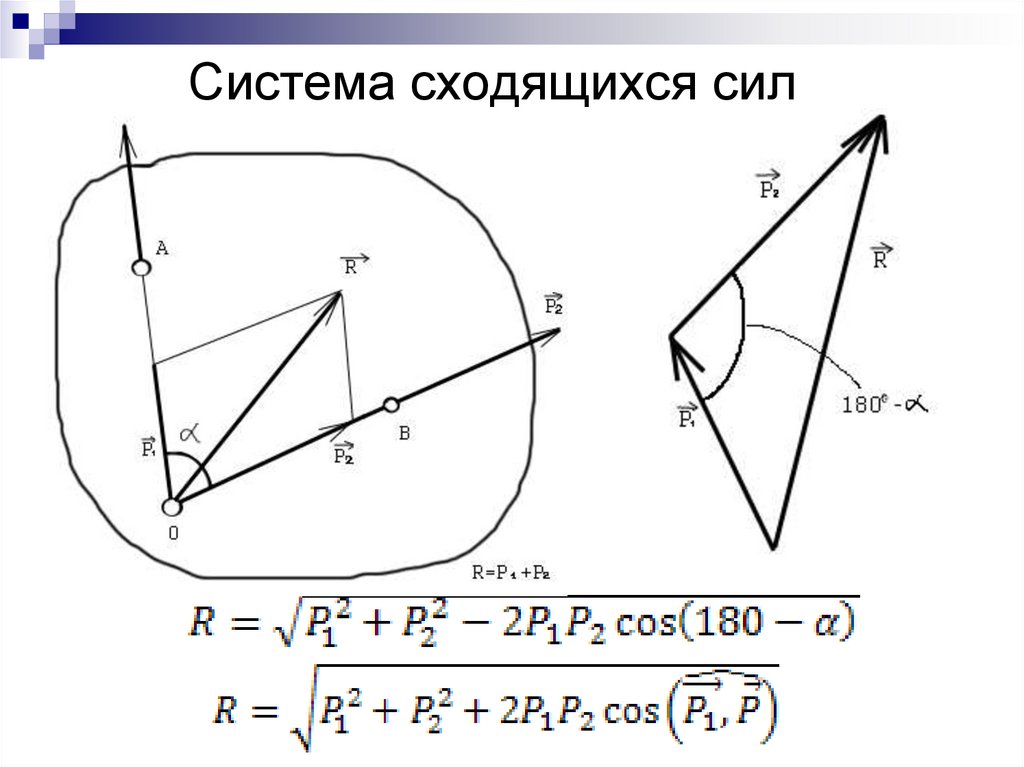
12. Система сходящихся сил

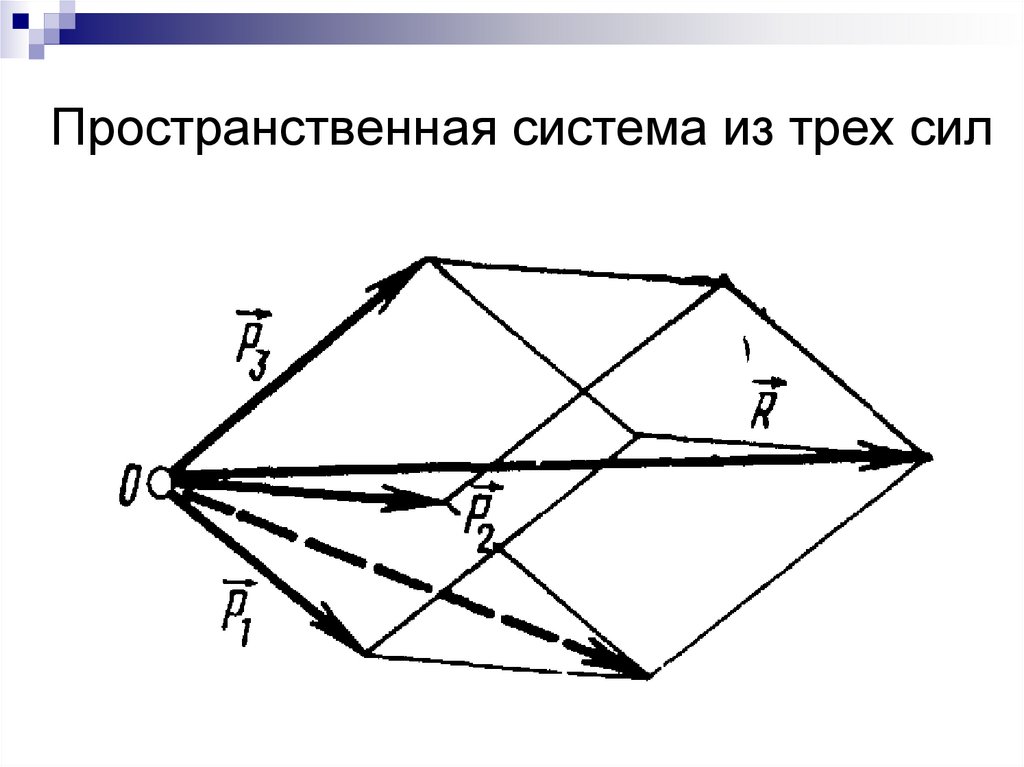
13. Пространственная система из трех сил

14.

15. Равновесие системы сходящихся сил

16. Теорема о трёх силах

17. Сходящиеся силы, приложенные к самолёту

Ra – аэродинамическая сила крыла

18. G – сила тяжести (вес ВС), P – тяга винта (или газотурбинного двигателя), Xa – сила лобового сопротивления ВС Ya –

аэродинамическая подъемная сила

19. Теорема Вариньона о моменте равнодействующей сходящейся системы сил

n
R Fi
i 1
n
R х Fiх
i 1
m0 ( F1 ) 2пл. ОАВ ОА Оb ОА F1x
m0 ( R) m0 ( Fi )
n
i 1

20. Момент силы, относительно центра, представленный в виде вектора

r P 2 S AOB
mo ( P) r P

21.

m0 ( P) 2 0,5Ph 2 S AOB
m0 ( P) Ph

22. Пара сил. Момент пары

23. Момент пары, как вектор

mo ( P) mo ( P ) M ( P, P )

24. Сложение пар. Равновесие тела под действием системы пар

25. ЭКВИВАЛЕНТНОСТЬ ПАР

Действие пары на тело
не изменится, если эту
пару заменить любой
другой парой, лежащей в
той же плоскости и
имеющей то же момент.

26.

Свойства пары сил:
1. Действие пары на тело не изменится,
если переместить пару в другое
положение в плоскости ее действия.
2. Действие пары на тело не изменится,
если одновременно изменить модуль сил
пары и величину ее плеча, сохраняя при
этом численное значение и знак,
момента пары.

27. Теорема Пуансо о параллельном переносе сил

28. Привидение к точке плоской системы произвольно расположенных сил

n
Fгл Fк
М гл0
n
m0 ( Fk )
k 0
0
n
Fгл y Fкy
0
n
Fглx Fкx
0
М гл0 m1 m2 m3 mn
2
2
F Fгл
Fгл
x
y

29. Точку приложения равнодействующей можно определить по формуле

M гл
d
Fгл
где d – расстояние от выбранной точки приведения до
точки приложения равнодействующей;
Мгл – величина главного момента относительно
выбранной точки приведения;
Fгл – величина главного вектора системы сил.

30.

31.

Основная
равновесия:
форма
уравнения

32.

Теорема Вариньона о моменте
равнодействующей
произвольной плоской системы сил
Mo
ОА d
R
Mo
mo ( R) Rd R
Mo
R
M o mo ( Fi )
n
i 1
n
mo ( R) mo ( Fi )
i 1

33. Пространственная система сил

Moo(F) = np. F·a,
a – расстояние от оси до проекции F;
np. F – проекция силы на плоскость,
перпендикулярную оси
np. F = Fcos ; МОО(F) = F cos ·a.

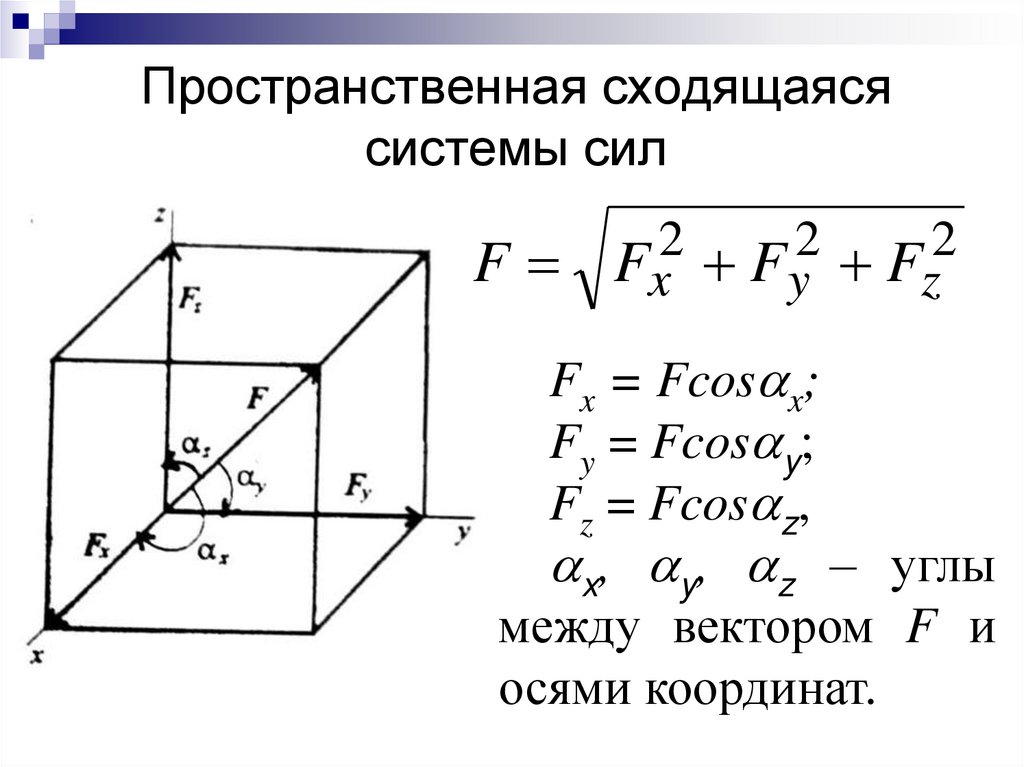
34. Пространственная сходящаяся системы сил

F
2
2
2
Fx Fy Fz
Fx = Fcos x;
Fy = Fcos y;
Fz = Fcos z,
x, y, z – углы
между вектором F и
осями координат.

35. Пространственная сходящихся системы сил

36. .

F x
F z
z ( F F z )
Fkx
F y
k 1
n
Fky
k 1
n
Fkz
k 1
F
x ( F F x ) соs F x
x
F
y ( F F y )
n
2
2
2
F x F y F z
cos y
F y
F
F z
cos z
F

37. Произвольная пространственная система сил

38.

Fгл
Fгл x
М гл
n
Fkx
k 1
n
mk
k 1
M гл y
n
mky
k 1
2
2
2
Fгл x Fгл y Fгл z
Fгл y
n
Fky
k 1
M гл
M гл x
Fгл z
n
Fkz
k 1
2
2
2
M гл x M гл y M гл z
n
mkx
k 1
M гл z
n
mkz
k 1

39.

Уравнения равновесия
пространственной системы сил
n
Fkx 0
k 1
n
mkx ( Fk ) 0
k 1
n
Fky 0
k 1
n
mky ( Fk ) 0
k 1
n
Fkz 0
k 1
n
mkz ( Fk ) 0
k 1

40.

Сила
тяжести

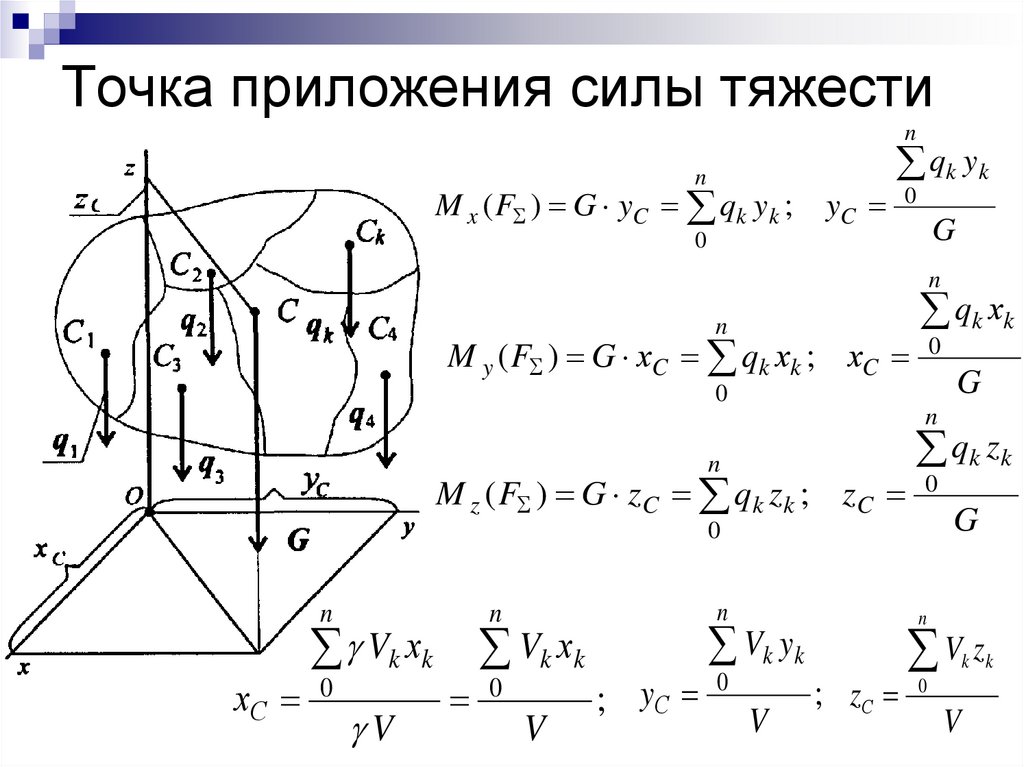
41. Точка приложения силы тяжести

n
n
M x ( F ) G yC qk yk ;
yC
qk y k
0
G
0
n
n
q k хk
0
G
M y ( F ) G хC qk хk ; хC
0
n
n
qk z k
0
G
M z ( F ) G zC qk z k ; zC
n
хС
Vk хk Vk хk
0
n
n
V
0
V
; yС
n
Vk yk
0
V
0
; zС
V z
k k
0
V

42. Определение координат центра тяжести плоских фигур

Для плоских тел: V = Ah,
где А – площадь фигуры, h – ее высота
n
хС
Аk h хk
0
Ah
n
n
Ak хk
0
A
;
yС
Ak yk
0
A
;
h
zС .
2
Координаты центра тяжести сечения можно выразить
через статический момент:
n
0
Ak yk S x
хС
Sу
А
n
Ak хk
0
Sу
Sx
yС
А

43.

44.

45.

46.

При решении задач используются следующие методы:
1) Аналитический (интегрированием)

47.

Пример. Определить положение центра тяжести для тонкой
однородной пластины, форма и размеры которой, в
сантиметрах

48.

Решение.
Данную фигуру представляем состоящей из трех простых
фигур: 1 – прямоугольник, 2 – круга, 3 – треугольника.
Площади кругового и треугольного отверстий вводим в
расчет со знаком минус, а площадь прямоугольника – без
учета имеющихся в нем отверстий.
Площади простых фигур:
Высота треугольника

49.

Координаты центра тяжести простых фигур:
х1=31/2=15,5 см,
х2=8см,
х3=31-6-12/3=21см,
где 12/3 – расстояние от центра тяжести треугольника до
его основания, равное 1/3 высоты.
Координата центра тяжести заданной фигуры

50. Центровка самолёта

m1 x1 m2 x2 ... mn xn
хС
m
m1 y1 m2 y2 ... mn yn
yС
m

51.

xC xa
x
100 %
ba
x
x 100 %
ba

52.

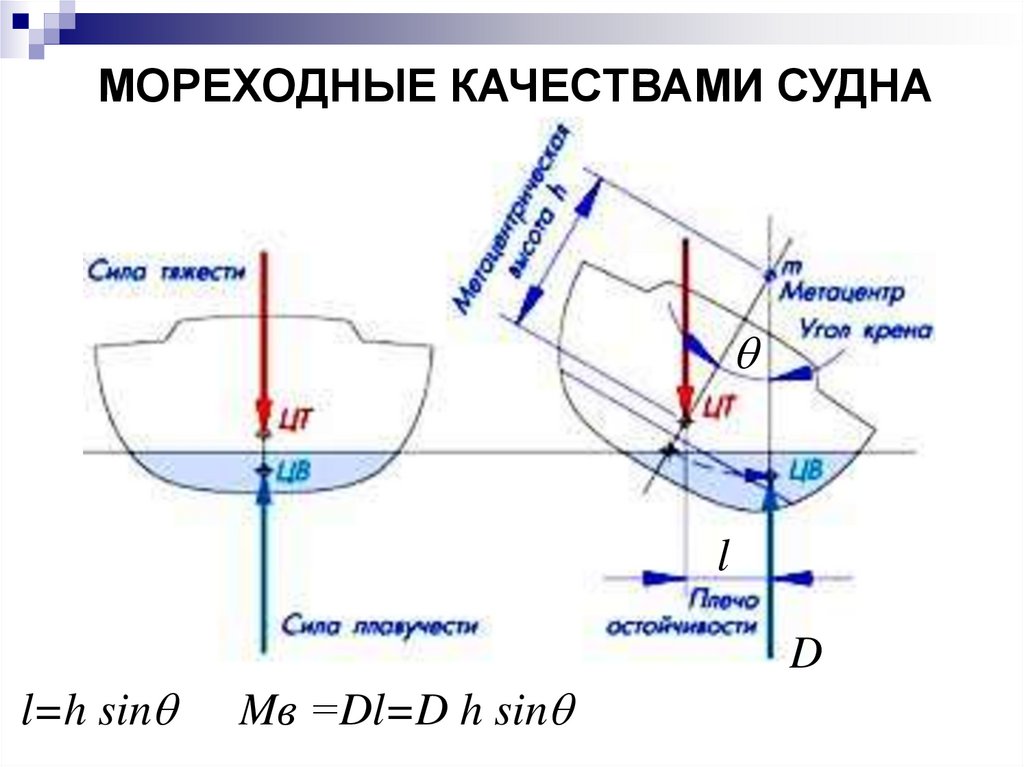
МОРЕХОДНЫЕ КАЧЕСТВАМИ СУДНА
q
l
l=h sinq
Mв =Dl=D h sinq
D

53.

54.

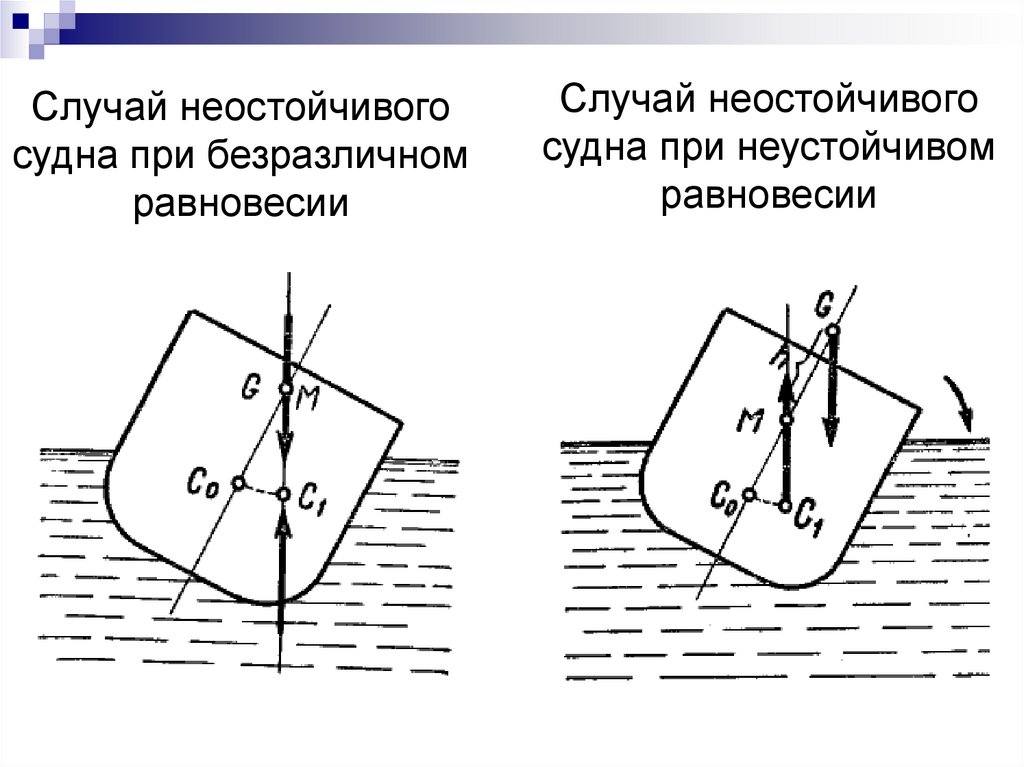
Случай остойчивого судна

55.

Случай неостойчивого
судна при безразличном
равновесии
Случай неостойчивого
судна при неустойчивом
равновесии

56.

Для классической яхты “Contessa
32” потеря остойчивости
наступает только при крене 155°

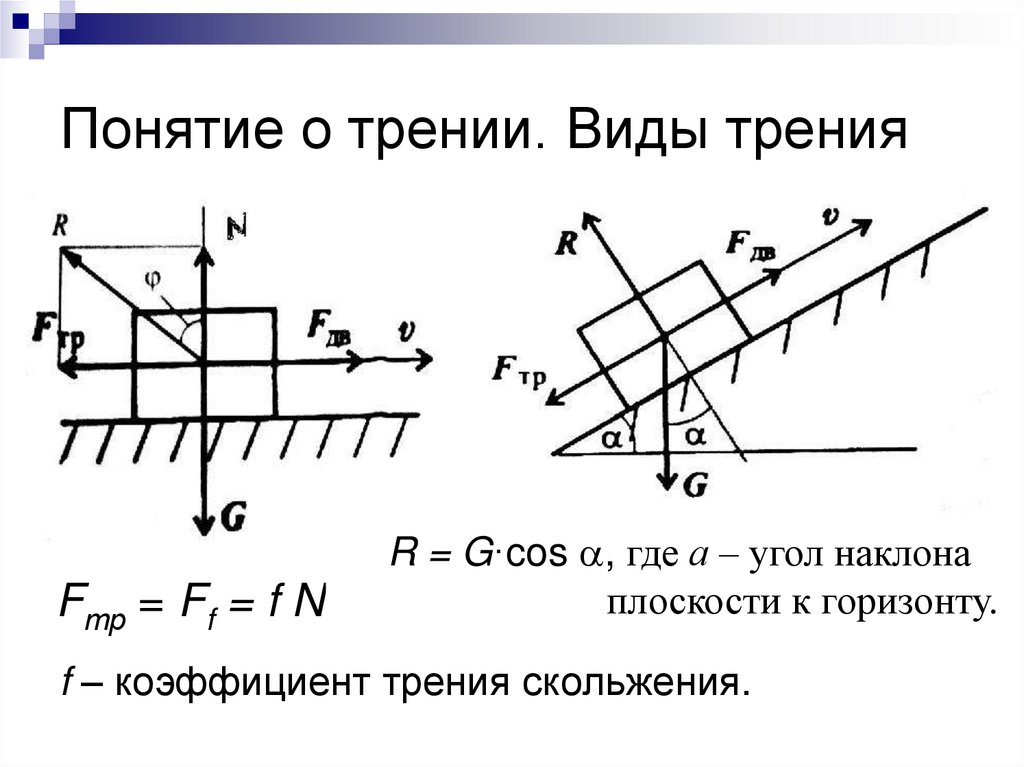
57. Понятие о трении. Виды трения

Fтр = Ff = f N,
R = G·cos , где а – угол наклона
плоскости к горизонту.
f – коэффициент трения скольжения.

58.

0 < Ff < Ff 0
– статическая сила трения (сила трения
Ff 0
покоя);
Ff – динамическая сила трения
Угол трения
tg 0
Fтр.max
N
f0N
f0
N

59. .

До тех пор пока линия действия равнодействующей всех
сил, приложенных к телу, проходит внутри конуса
трения, скольжение тела по связи не возникает
0

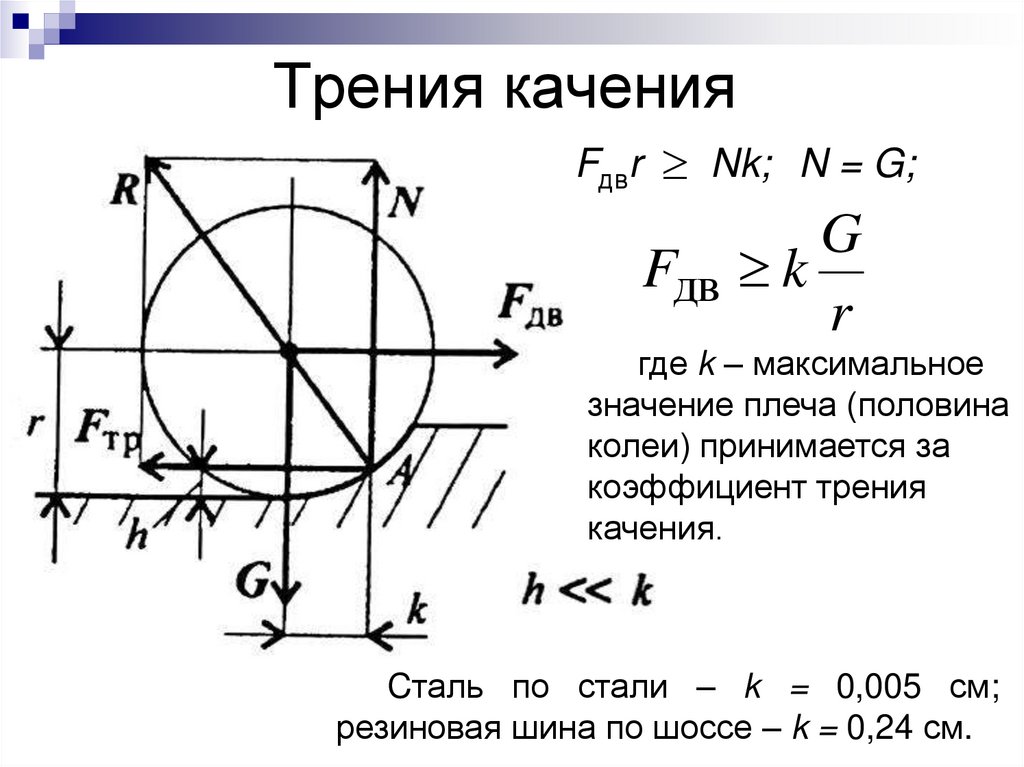
60. Трения качения

Fдвr
Nk; N = G;
G
Fдв k
r
где k – максимальное
значение плеча (половина
колеи) принимается за
коэффициент трения
качения.
Cталь по стали – k = 0,005 см;
резиновая шина по шоссе – k = 0,24 см.