Similar presentations:
Теоретическая механика. Статика
1. Теоретическая механика Статика
Лекция № 42. 4.1 Момент силы относительно оси
Моментом mZсилы F
относительно оси
Z называется
проекция момента mО
этой силы
относительно
центра О, лежащего
на этой оси, на эту
ось.
Z
mO
B
mZ
F
α
h
O
mZ mO Z mO cos .
r
3.
ЖУКОВСКИЙНиколай
Егорович
(1847-1921), русский ученый, основоположник
современной гидро- и аэромеханики. С 1872
до конца жизни преподавал математику и
механику. Для иллюстрации своих лекций он
сконструировал множество приборов и
механизмов.
В своей речи “О воздухоплавании” (1898)
“отец
русской
авиации”
предсказывал:
“Человек не имеет крыльев и по отношению
веса своего тела к весу мускулов в 72 раза
слабее птицы, но я думаю, что он полетит,
опираясь не на силу своих мускулов, а на силу
своего разума”.
В конце 1918 Жуковский основывает
Центральный
аэрогидродинамический
институт. Организованные им теоретические
курсы
для
военных
летчиков
были
реорганизованы в Институт инженеров
воздушного флота (с 1922 — Военновоздушная инженерная академия имени
Жуковского).
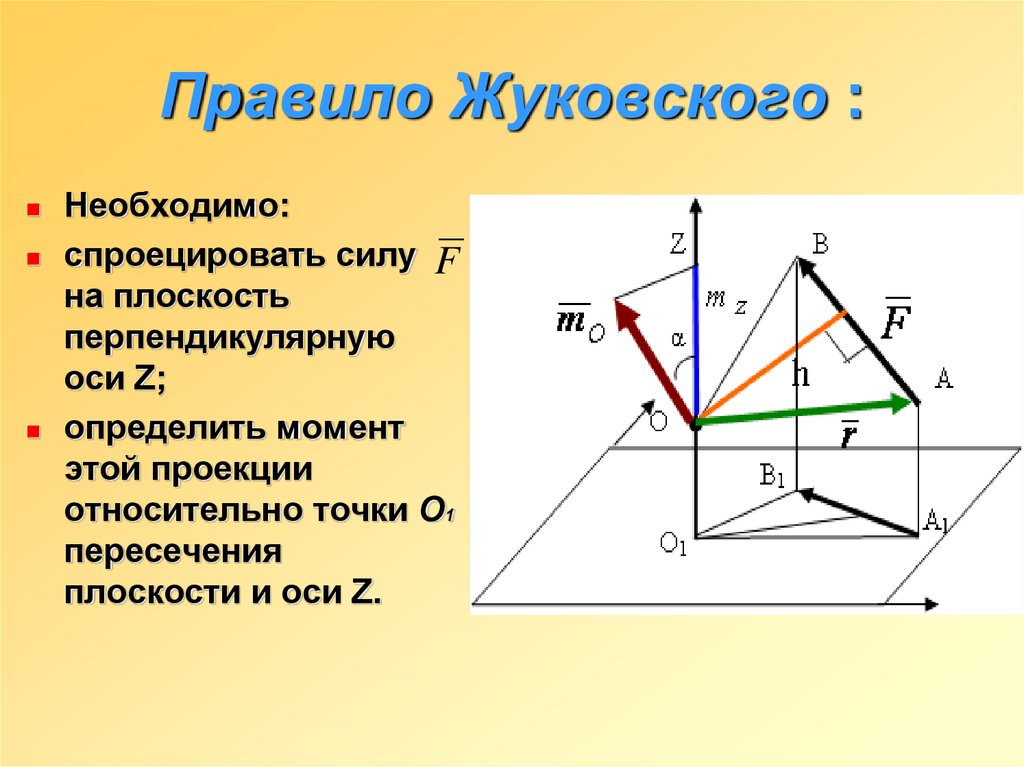
4. Правило Жуковского :
Необходимо:спроецировать силу F
на плоскость
перпендикулярную
оси Z;
определить момент
этой проекции
относительно точки O1
пересечения
плоскости и оси Z.
5.
ZZ
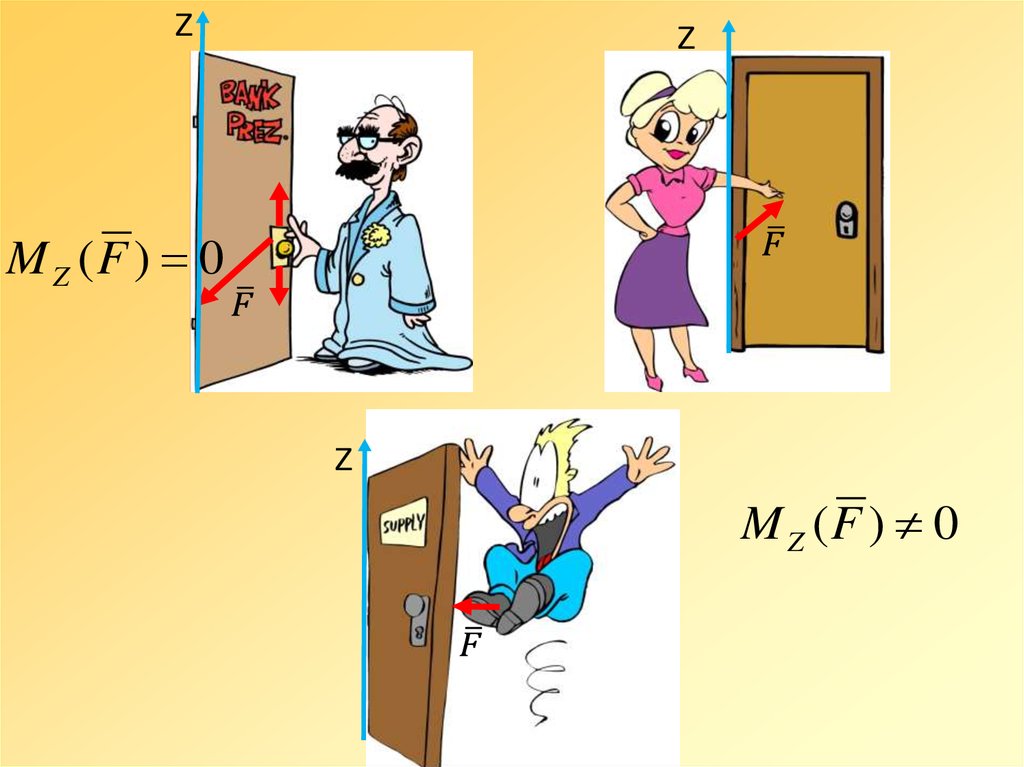
M Z (F ) 0
Z
M Z (F ) 0
6.
Момент силы F относительнооси Z равен нулю, если сила и ось
лежат в одной плоскости, так как в
этом случае проекция силы на
плоскость перпендикулярную оси Z
пресечет эту ось (в частном случае
равна нулю), ее плечо равно нулю.
То есть, M Z ( F ) 0 ,
если вектор F параллелен или
пересекает ось Z.
7. 4.2 Пространственная система сил
В векторной форме условиеравновесия произвольной
пространственной системы сил
имеет вид:
R 0; M O 0
8.
R 0; M O 0R R R R 0;
2
X
2
Y
2
Z
RX 0; RY 0; RZ 0;
F
kX
0; FkY 0; FkZ 0.
M O M M M 0;
2
X
M
X
2
Y
2
Z
0; M Y 0; M Z 0.
9. УРАВНЕНИЯ РАВНОВЕСИЯ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ В АНАЛИТИЧЕСКОЙ ФОРМЕ ИМЕЮТ ВИД:
FkX
M
kX
0; FkY 0; FkZ 0;
0; M kY 0; M kZ 0.
10.
Для нахождения моментов силотносительно координатных осей
используют правило
Жуковского и
теорему Вариньона: Момент
равнодействующей
относительно оси равен сумме
моментов составляющих сил
относительно этой оси.
11.
Для этого силы,действующие на тело,
раскладывают на
составляющие
параллельные осям
координат и находят
моменты этих
составляющих относительно
12. Пример 1
Момент силы Fотносительно оси
OX равен:
Z
b
F sin b
F
Момент силы F
относительно оси
OY равен:
F sin а
Момент силы F
относительно оси
OZ равен: 0
c
FZ
a
β
FY
X
α
Y
FX
13. Пример 2
Момент силы Fотносительно оси
OX равен:
Z
b
F sin c
Момент силыF
относительно оси
OY равен: 0
a
Момент силыF
относительно оси X
OZ равен: 0
FY
FZ
c
α
F
Y
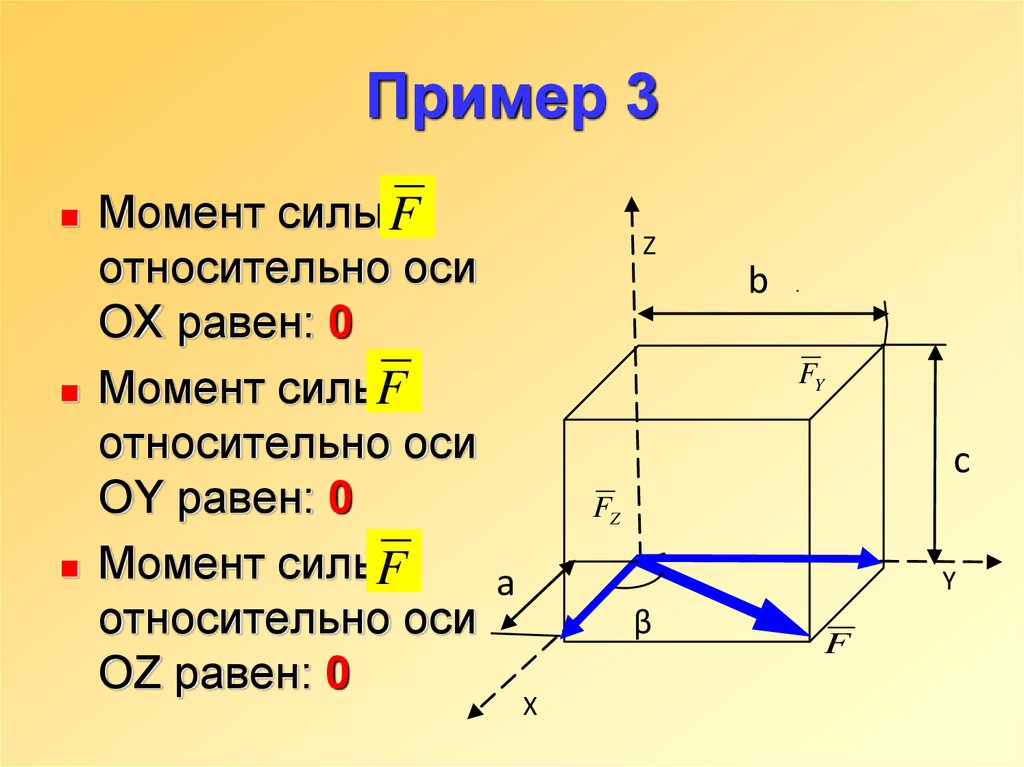
14. Пример 3
Момент силы Fотносительно оси
OX равен: 0
Момент силыF
относительно оси
OY равен: 0
Момент силыF
a
относительно оси
OZ равен: 0
Z
b
FY
c
FZ
Y
β
X
F
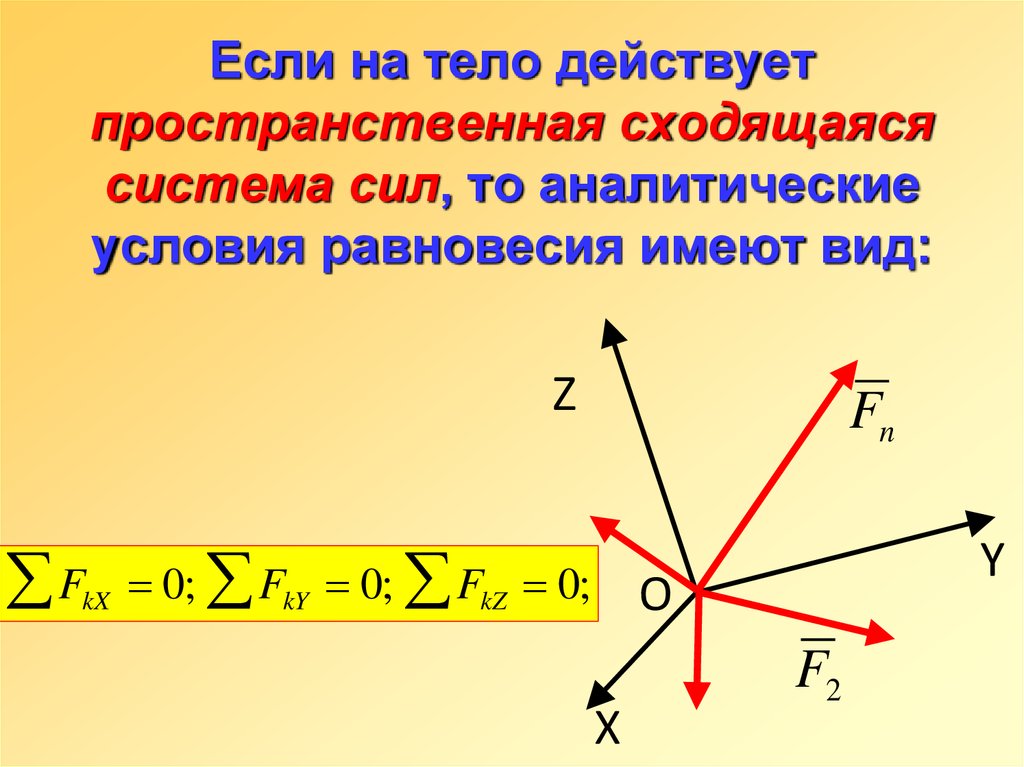
15. Если на тело действует пространственная сходящаяся система сил, то аналитические условия равновесия имеют вид:
ZF
kX
Fn
0; FkY 0; FkZ 0;
Y
O
X
F2
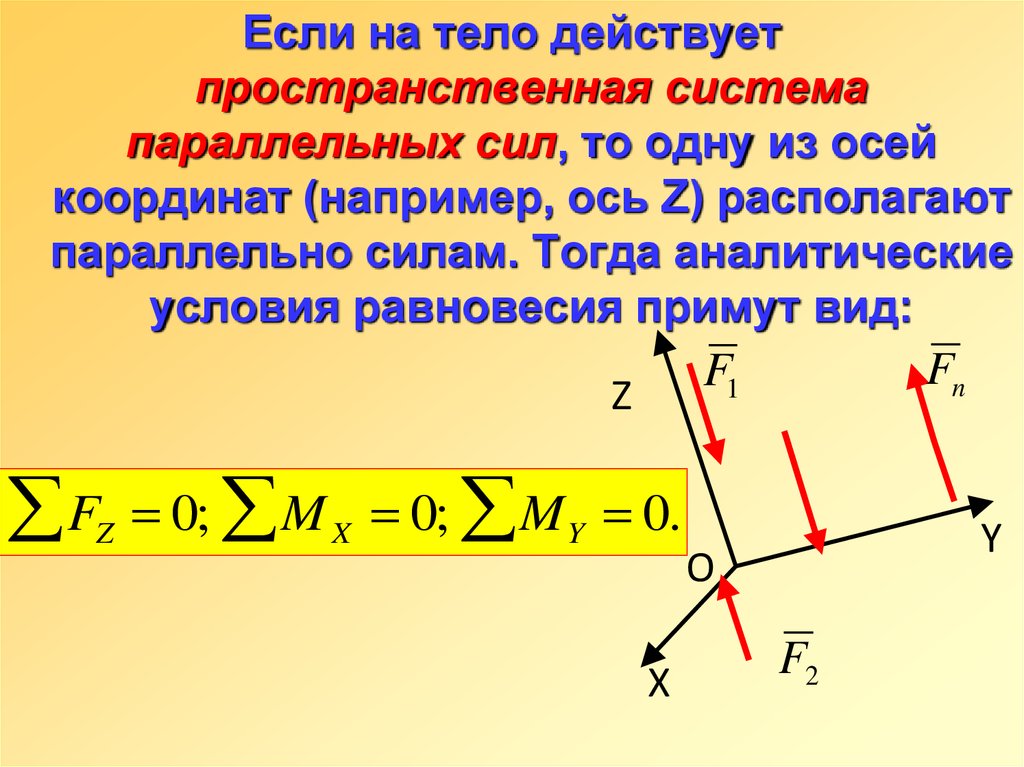
16. Если на тело действует пространственная система параллельных сил, то одну из осей координат (например, ось Z) располагают
параллельно силам. Тогда аналитическиеусловия равновесия примут вид:
Fn
F
1
Z
F
Z
0; M X 0; M Y 0.
X
Y
O
F2
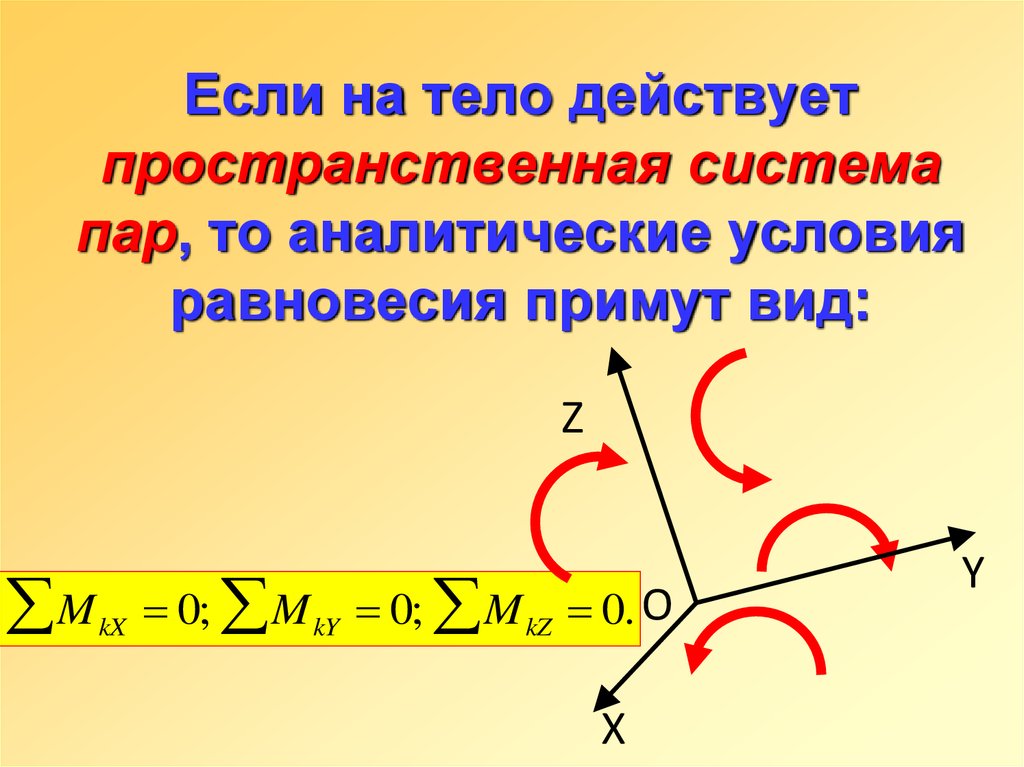
17. Если на тело действует пространственная система пар, то аналитические условия равновесия примут вид:
ZM
kX
0; M kY 0; M kZ 0. O
X
Y
18.
СИСТЕМА СИЛпространственная
плоская
произвольная
1) FkX 0; FkY 0; mO ( Fk ) 0.
F
M
2) FkX 0; mA ( Fk ) 0; mB ( Fk ) 0,
0; FkY 0; FkZ 0;
kX
kX
OX не AB.
0; M kY 0; M kZ 0.
3) mA ( Fk ) 0; mB ( Fk ) 0; mC ( Fk ) 0,
точки A, B, C не лежат на одной прямой .
параллельные
1) FkY 0; M O 0
F
Z
точка О любая в плоскости О1 XY
0; M X 0; M Y 0.
2) M A 0; M B 0;
AB не паралльны силам
сходящаяся
F
kX
0; FkY 0; FkZ 0;
F
kX
0; FkY 0.
система пар
M
kX
0; M kY 0; M kZ 0.
m
k
0












 physics
physics








