Курс лекций по теоретической механике. Статика

1.

Курс лекций по
теоретической механике

2.

Состав курса:
1. Лекционный курс
2. Практические занятия
3. Самостоятельная работа :
- Решение задач.
- Выполнение и защита расчетно-графических
работ (РГР) или контрольная работа
Рекомендуемая литература
Яблонский А.А., Норейко С.С.Сборник заданий для
курсовых работ по теоретической механике: 16-е
изд.Москва: Интеграл- Пресс, 2007
2. Тарг С.М.Краткий курс теоретической механики. Учебник
для вузов. 17-е изд.Москва: Высшая школа, 2007
3. Мещерский И.В.Задачи по теоретической механике: 47 изд.
стереот.Санкт-Петербург: Лань, 2007
4. Белуха В.Ф., Костин В.Е., Саразов А.В., Худяков К.В.Курс
лекций по теоретической механике: Сборник "Учебные
2
пособия": Cерия "Естественнонаучные и технические
1.

3.

Теоретическая механика – изучает законы механического
движения и механического взаимодействия, общие для любых тел.
Теоретическая механика является базовой наукой, на основе
которой изучаются другие прикладные технические дисциплины.
Теоретическая механика состоит из трех разделов:
Статика
Кинематика
Динамика
Статика – изучает условия относительного равновесия
механических систем.
Кинематика –изучает механическое движение без учета сил,
вызывающих это движение.
Динамика – изучает механическое движение с учетом сил,
вызвавших данное движение.
3

4.

Теоретическая механика.
Раздел 1 – СТАТИКА
ВВЕДЕНИЕ В СТАТИКУ
УСЛОВИЯ РАВНОВЕСИЯ
ЦЕНТР ТЯЖЕСТИ
4

5.

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Статика - раздел теоретической механики, в котором
изучаются условия равновесия
находящихся под действием сил.
материальных
тел,
Равновесие - это состояние покоя тела по
отношению к другим телам, например по отношению к
Земле.
Абсолютно твердое тело - такое тело,
расстояние между элементами которого всегда
остается постоянным.
5

6.

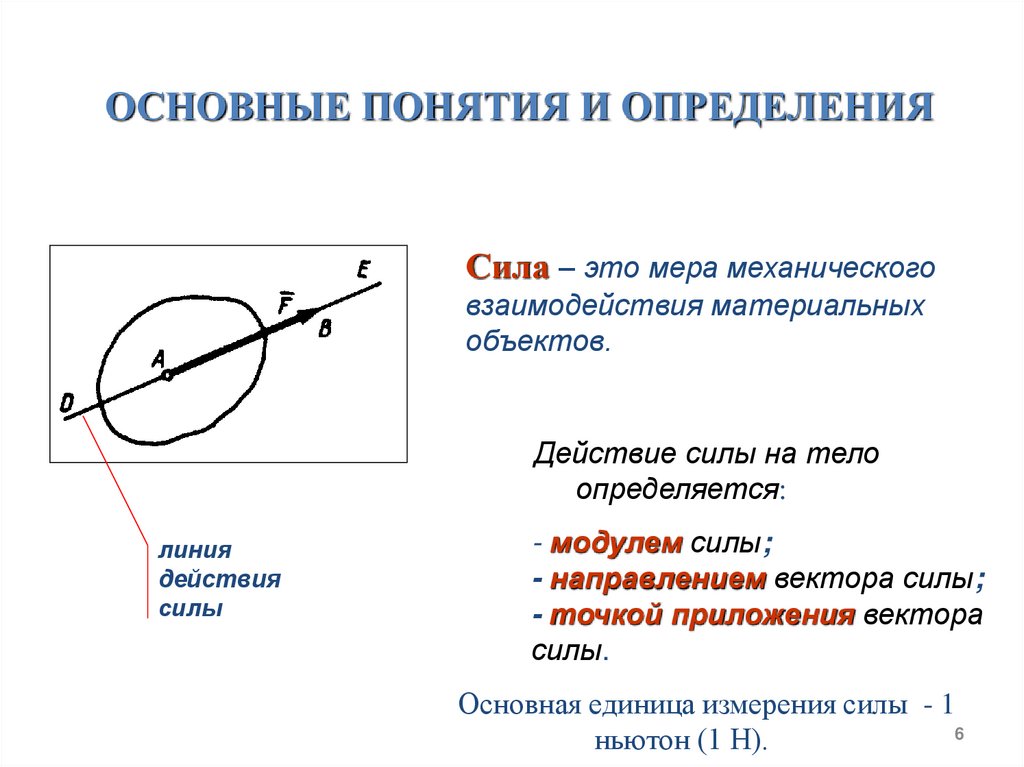
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Сила – это мера механического
взаимодействия материальных
объектов.
Действие силы на тело
определяется:
линия
действия
силы
- модулем силы;
- направлением вектора силы;
- точкой приложения вектора
силы.
Основная единица измерения силы - 1
6
ньютон (1 Н).

7.

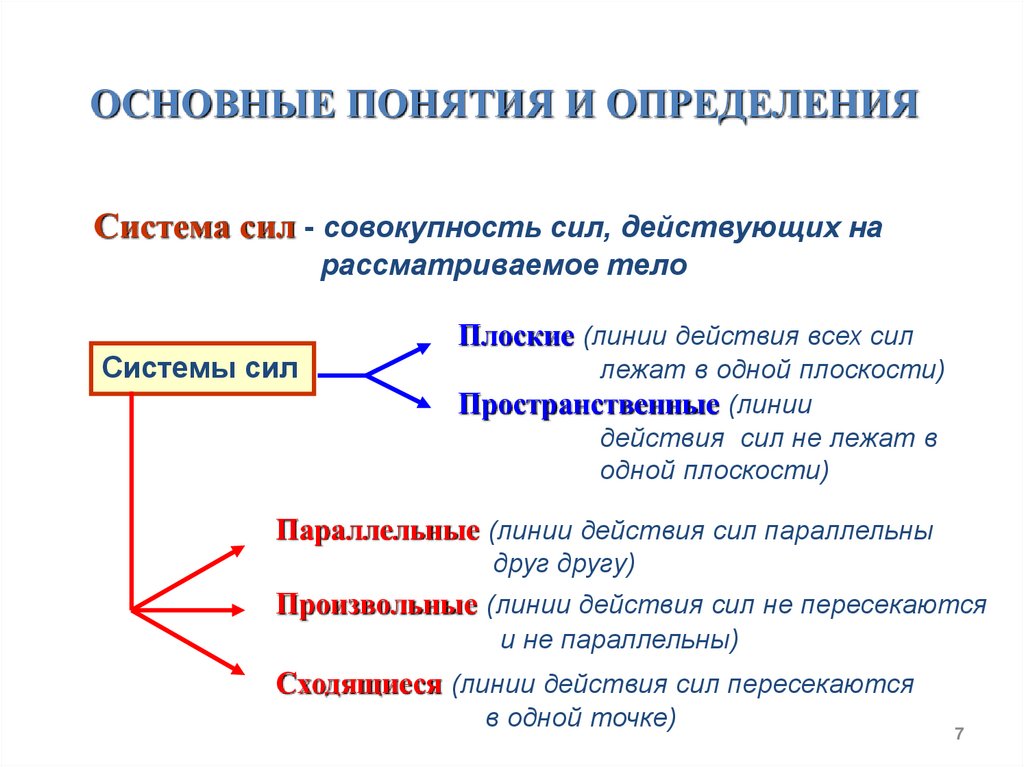
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Система сил - совокупность сил, действующих на
рассматриваемое тело
Системы сил
Плоские (линии действия всех сил
лежат в одной плоскости)
Пространственные (линии
действия сил не лежат в
одной плоскости)
Параллельные (линии действия сил параллельны
друг другу)
Произвольные (линии действия сил не пересекаются
и не параллельны)
Сходящиеся (линии действия сил пересекаются
в одной точке)
7

8.

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Эквивалентными называются две системы сил,
приводящие тело к одному и тому же кинематическому
состоянию.
Уравновешенная (эквивалентная нулю) – это такая
система сил, под действием которой свободное твердое
тело может находиться в покое.
Равнодействующей системы сил, называется
сила, эквивалентная данной системе сил.
Сила, приложенная к телу в какой-нибудь одной его точке,
называется сосредоточенной.
Силы, действующие на все точки объема или части
поверхности тела, называются распределенными.
8

9.

АКСИОМЫ СТАТИКИ
1. Если на свободное абсолютно твердое
тело действуют две силы, то тело
может находиться в равновесии тогда и
только тогда, когда эти силы равны по
модулю (F1 = F2) и направлены вдоль
одной прямой в противоположные
стороны
2. Действие данной системы сил на абсолютно твердое тело не
изменяется, если к ней прибавить или от нее отнять уравновешенную
.
систему сил
Следствие: действие силы на абсолютно твердое тело не
изменится, если перенести точку приложения силы вдоль ее
линии действия в любую другую точку тела.
9

10.

АКСИОМЫ СТАТИКИ
3. Закон параллелограмма сил: две силы, приложенные к телу в
одной точке, имеют равнодействующую, приложенную в той же
точке и изображаемую диагональю параллелограмма,
построенного на этих силах, как на сторонах
R F1 F2
10

11.

АКСИОМЫ СТАТИКИ
4. Закон равенства действия и
противодействия: при всяком
действии одного материального
тела на другое имеет место
такое же численно, но
противоположное по направлению
противодействие, т.е.
5. Принцип отвердевания: равновесие изменяемого (деформируемого)
тела, находящегося под действием уравновешенной системы сил,
возможно только при его «отвердевании»
11

12.

СВЯЗИ И ИХ РЕАКЦИИ
Свободным называется тело, которое может совершать
из данного положения любые перемещения в пространстве
Несвободным называется тело, перемещениям которого в
пространстве препятствуют какие-нибудь другие, скрепленные
или соприкасающиеся с ним, тела (связи)
Реакция связи – это сила, с которой связь действует на
тело, препятствуя его перемещениям, называется.
Принцип освобождаемости от связей: всякое
несвободное тело можно рассматривать как свободное, если
действие связей заменить их реакциями, приложенными к данному
телу
12

13.

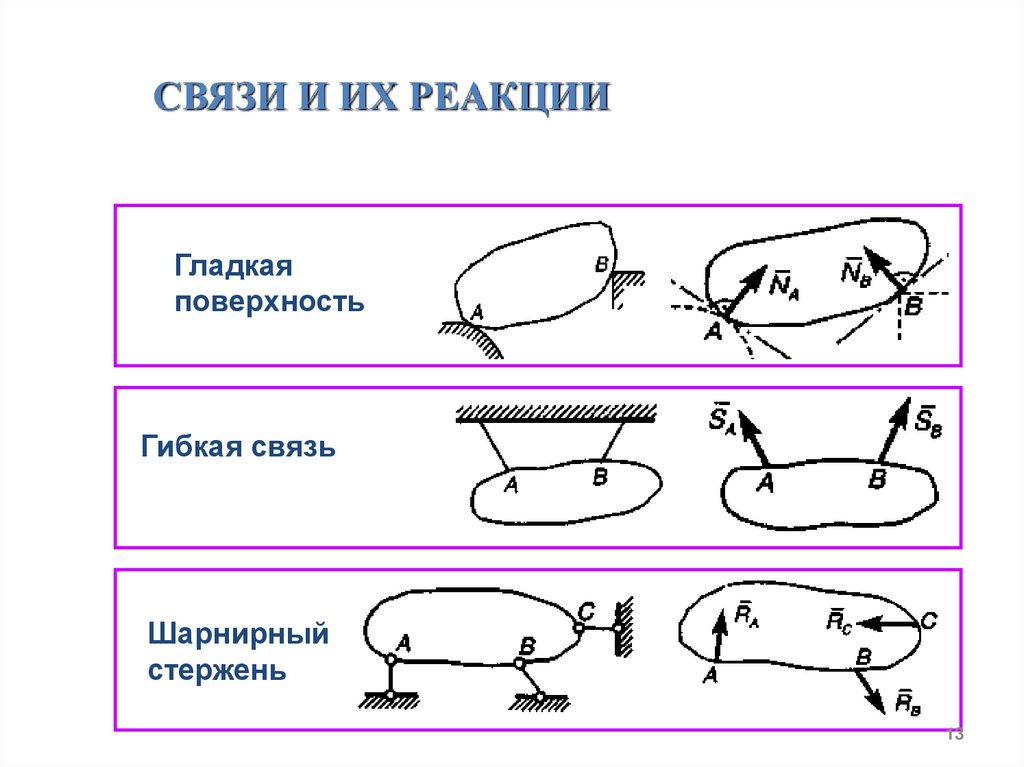
СВЯЗИ И ИХ РЕАКЦИИ
Гладкая
поверхность
Гибкая связь
Шарнирный
стержень
13

14.

СВЯЗИ И ИХ РЕАКЦИИ
Шарнирно-неподвижная опора
Цилиндрический шарнир
Шарнирноподвижная опора
Жесткая заделка
14

15.

ПРОЕКЦИИ СИЛ
Проекция силы на ось - алгебраическая величина,
равная произведению модуля силы на косинус угла между
силой и положительным направлением оси:
Fx = Fcos = ab;
Qx= Qcos 1=
= -Qcos = -de
Px = 0
15

16.

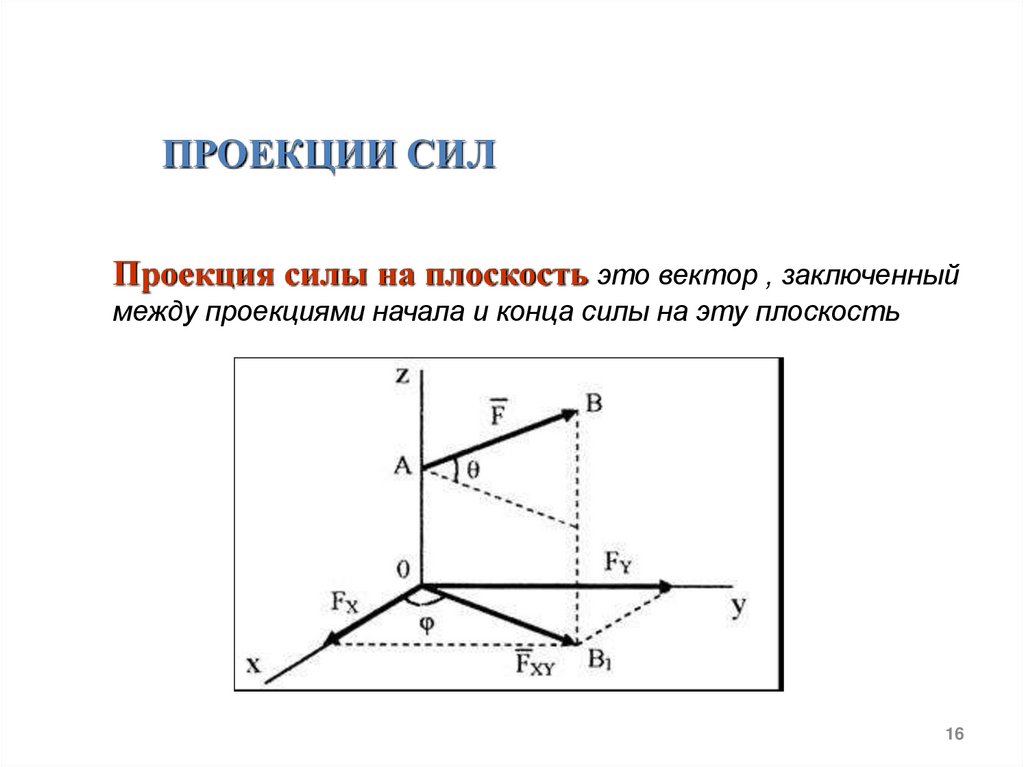
ПРОЕКЦИИ СИЛ
Проекция силы на плоскость это вектор , заключенный
между проекциями начала и конца силы на эту плоскость
16

17.

ПРОЕКЦИИ СИЛ
Силу можно задавать ее проекциями Fx, Fy, Fz
на координатные оси: 2
2
2
F Fx Fy Fz
cos Fx / F ,
cos Fy / F ,
cos Fz / F
F Fx2 Fy2 Fz2
cos Fx / F ,
cos Fy / F ,
cos Fz / F
17

18.

СПОСОБЫ СЛОЖЕНИЯ И
РАЗЛОЖЕНИЯ СИЛ
1. Сложение двух сил
Величину, равную геометрической сумме сил системы,
называют главным вектором этой системы сил
R F1 F2
R F12 F22 2F1F2 cos
18

19.

СПОСОБЫ СЛОЖЕНИЯ И
РАЗЛОЖЕНИЯ СИЛ
2. Сложение системы сил
n
R F1 F2 Fn Fk
i 1
19

20. Введение в статику

2.7
Введение в статику
Аналитический способ сложения сил
R Rx2 R y2 Rz2 ;
Rx = Fkx;
Ry = Fky;
Rz = Fkz
cos Rx / R ,
cos Ry / R ,
cos Rz / R.
F
Разложение сил
F F1 F2
20

21.

Момент силы относительно точки
Векторный момент силы относительно
центра О - это приложенный в центре О
вектор
М 0 (F ) r F
где OA r - радиус-вектор точки А,
проведенный из центра О.
Алгебраический момент силы
относительно центра
М0 (F) = ± F h.
М0( P ) = P h1, М0(Q ) = - Q h2
21

22.

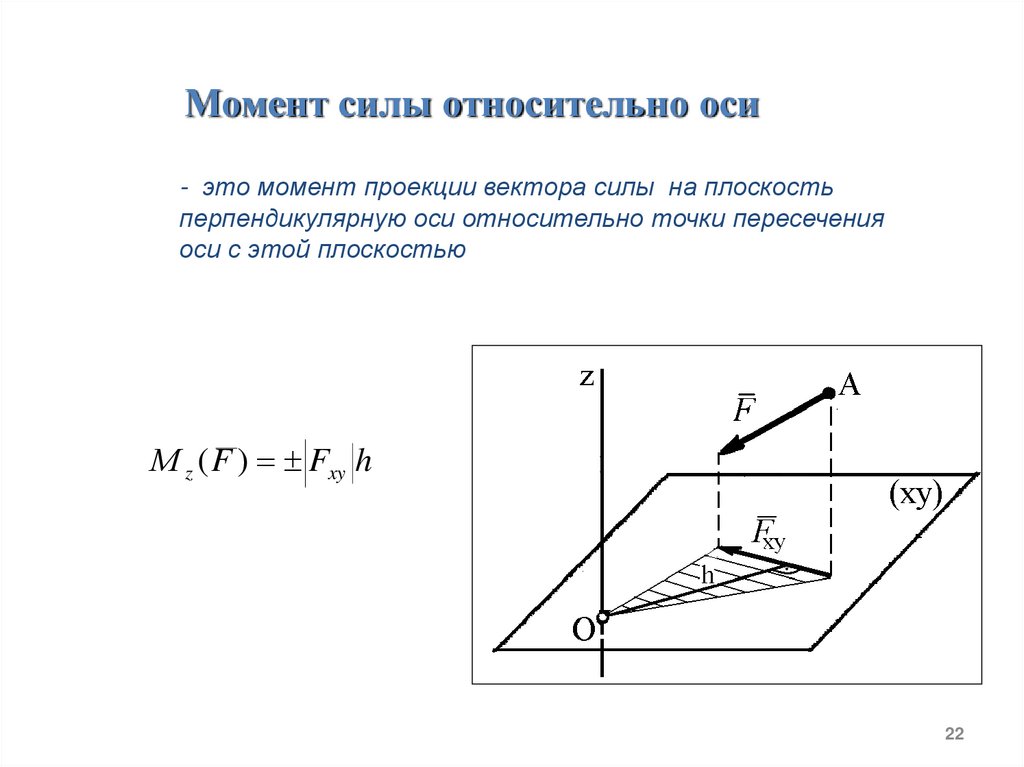
Момент силы относительно оси
- это момент проекции вектора силы на плоскость
перпендикулярную оси относительно точки пересечения
оси с этой плоскостью
М z ( F ) Fxy h
22

23.

Пара сил, момент пары
Плоскость действия пары - плоскость, проходящая
через линии действия сил пары
Алгебраический момент пары
М=±Fd
Плечо пары d - кратчайшее расстояние между
линиями действия сил пары
Векторный момент пары - это вектор М ,
направленный перпендикулярно плоскости действия
пары в ту сторону, откуда пара видна стремящейся
повернуть тело против хода часовой стрелки
Этот вектор называется скользящим
23

24.

Теорема о параллельном переносе силы
(лемма Пуансо)
Силу, приложенную к абсолютно твердому телу, можно,
не изменяя её действия, переносить из данной точки в
новый произвольный центр, прибавляя при этом пару с
моментом, равным моменту переносимой силы
относительно нового центра
24

25.

Приведение системы сил к центру
(Основная теорема
статики. Теорема об упрощении пр. пр. с.с.)
( F1 , F2 ,...,Fn ) ( F1' , F2' ,...,Fn ' ) (m1 ,m2 ,...,mn )
F1 F1 , и т д.
m1 m0 ( F1) и тт.д
( F1 , F2 ,...,Fn ) R ,M o
.
R Fk
M 0 m0 ( Fk )
R - главный вектор системы сил;
M 0 - главный момент системы сил
относительно центра О
25

26.

Приведение системы сил к центру
Частные случаи приведения системы сил к центру:
R 0
данная система сил приводится к одной паре сил
M0 0
R 0
M0 0
данная система сил приводится к одной силе, т. е.
к равнодействующей
R 0
M0 0
данная система сил будет уравновешенной
26

27.

ТЕОРЕМА ВАРИНЬОНА
Пусть система сил
приводится к
равнодействующей
F1 , F2 ,...,Fn R
Приложим в точке С силу
R R
Система сил F1 , F2 ,...,Fn , R'
будет находиться в равновесии и для нее
M 0 0 или
m0 ( Fk ) m0 ( R ) 0
m0 ( R ) m0 ( R ) mo Fk
Если данная система сил имеет равнодействующую, то момент
равнодействующей относительно любого центра О равен сумме
моментов сил системы относительно того же центра
27

28.

УСЛОВИЯ РАВНОВЕСИЯ РАЗЛИЧНЫХ
СИСТЕМ СИЛ
Равновесие
пространственной
системы произвольно
расположенных сил
R 0
M0 0
Fkx 0,
Fky 0,
mx ( Fk ) 0,
m y ( Fk ) 0,
Fkz 0,
mz ( Fk ) 0.
Равновесие
пространственной
системы параллельных
сил
Fkx 0,
Fky 0,
mz ( Fk ) 0.
В случае, когда все
действующие на тело силы
параллельны оси z
28

29.

УСЛОВИЯ РАВНОВЕСИЯ РАЗЛИЧНЫХ
СИСТЕМ СИЛ
Равновесие системы сходящихся сил
R Fk 0
в геометрической
форме: необходимо и
Fkx 0, Fky 0, Fkz 0
достаточно, чтобы силовой многоугольник,
построенный из векторов сил, был замкнутым
в аналитической форме:
R Rx2 Ry2 Rz2 0, или
Rx = 0, Ry = 0, Rz = 0,
29

30.

УСЛОВИЯ РАВНОВЕСИЯ РАЗЛИЧНЫХ
СИСТЕМ СИЛ
Равновесие плоской системы произвольных сил
2
1
Fkx 0,
Fky 0,
m0 ( Fk ) 0
3
m A ( Fk ) 0,
mB ( Fk ) 0,
Fkx 0
ось Ох, не
перпендикулярна
прямой АВ
m A ( Fk ) 0,
mB ( Fk ) 0,
mC ( Fk ) 0
центры А, В и С,
не лежат
на одной прямой
30

31.

УСЛОВИЯ РАВНОВЕСИЯ РАЗЛИЧНЫХ
СИСТЕМ СИЛ
Равновесие плоской системы
параллельных сил
Fky 0 ,
m0 ( Fk ) 0
В случае, когда все
действующие на тело силы
параллельны оси Оу
m A ( Fk ) 0,
mB ( Fk ) 0
точки A и В
не должны лежать на прямой,
параллельной векторам сил.
31

32.

РАВНОВЕСИЕ СИСТЕМ ТЕЛ
Внутренние связи – это связи, соединяющие части конструкции
Два способа решения задач
на равновесие составной конструкции:
1 способ. Рассматривают равновесие всей конструкции как единое
целое (не учитывая реакции внутренних связей) и дополнительно
равновесие какой-нибудь одной или нескольких частей конструкции
с учетом реакций внутренних связей.
2 способ. Конструкцию расчленяют на части и рассматривают
равновесие каждой части, учитывая при этом реакции внутренних
связей. При этом реакции внутренних связей будут попарно равны
по модулю и противоположны по направлению.
32

33.

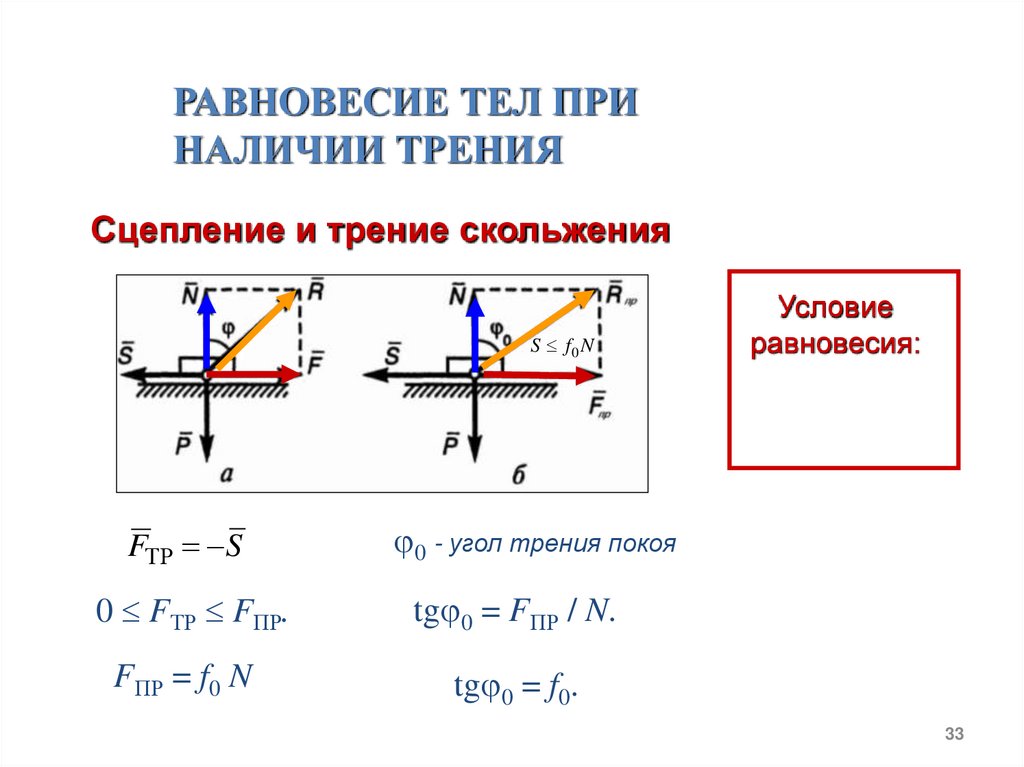
РАВНОВЕСИЕ ТЕЛ ПРИ
НАЛИЧИИ ТРЕНИЯ
Сцепление и трение скольжения
S f0 N
FТР S
0 - угол трения покоя
0 FТР FПР.
tg 0 = FПР / N.
FПР = f0 N
tg 0 = f0.
Условие
равновесия:
33

34.

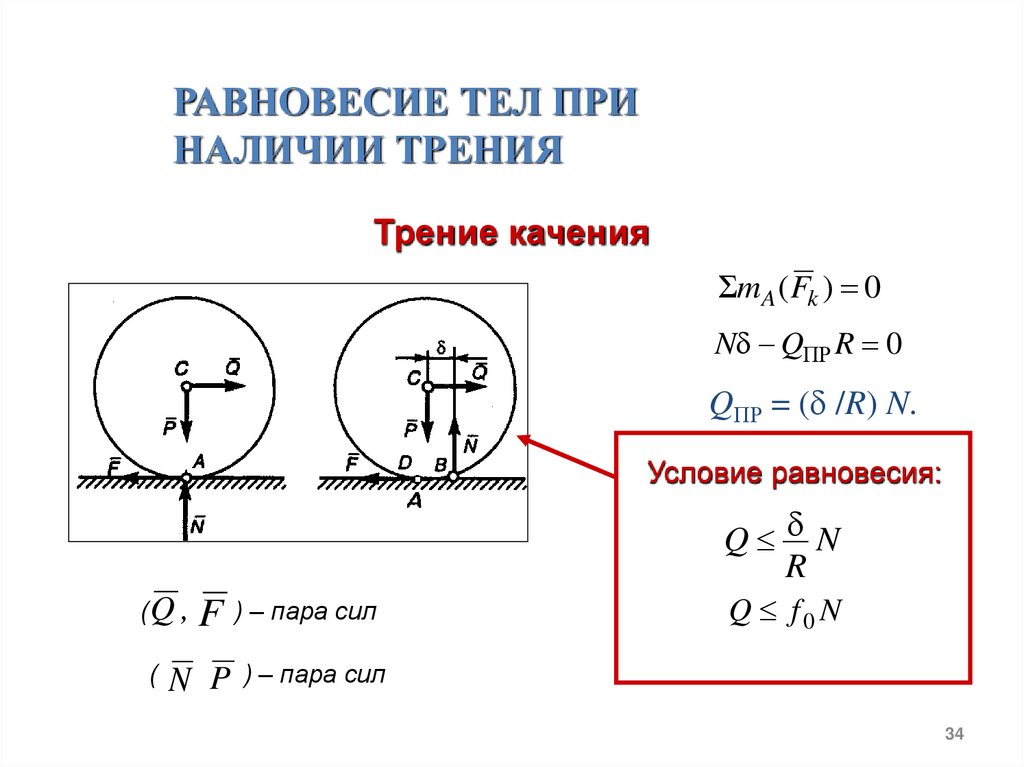
РАВНОВЕСИЕ ТЕЛ ПРИ
НАЛИЧИИ ТРЕНИЯ
Трение качения
mA ( Fk ) 0
N QПР R 0
QПР = ( /R) N.
Условие равновесия:
Q N
R
( Q , F ) – пара сил
( N
Q f0 N
P ) – пара сил
34

35.

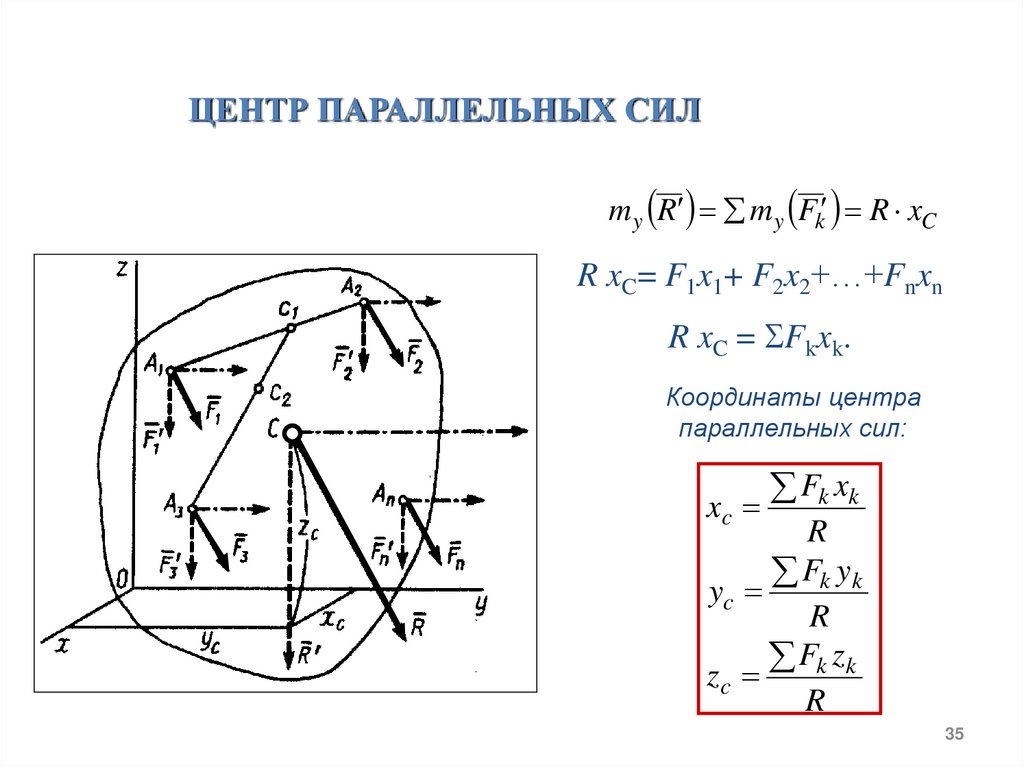
ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
m y R m y Fk R xC
R xC= F1x1+ F2x2+…+Fnxn
R xC = Fkxk.
Координаты центра
параллельных сил:
xc
Fk xk
R
Fk yk
yc
R
Fk zk
zc
R
35

36.

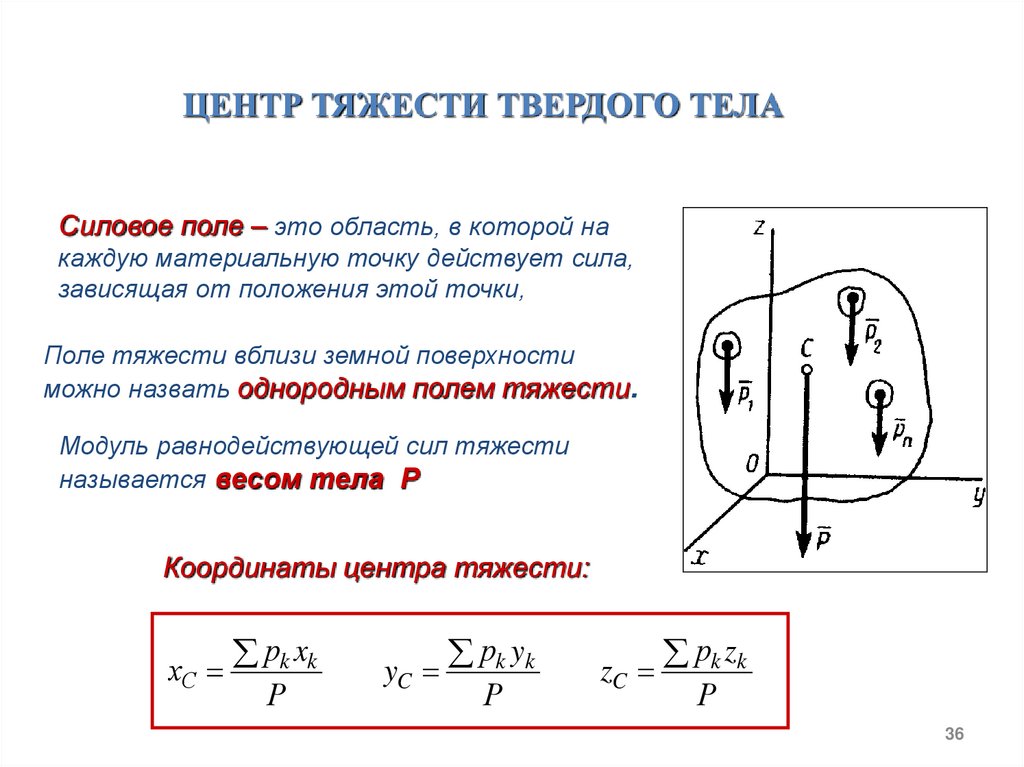
ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
Силовое поле – это область, в которой на
каждую материальную точку действует сила,
зависящая от положения этой точки,
Поле тяжести вблизи земной поверхности
можно назвать однородным полем тяжести.
Модуль равнодействующей сил тяжести
называется весом тела Р
Координаты центра тяжести:
хС
рk xk
Р
yC
рk yk
Р
zC
рk zk
Р
36

37.

ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
Центр тяжести некоторых однородных тел
1 Для однородного объемного твердого тела (вес пропорционален
объему):
V x
х k k
С
V
V y
y k k
C
V
Vk zk
z
C
V
2. Для тела, представляющего собой однородную пластину (вес
пропорционален площади):
Sk xk
х
С
S
S k yk
y
C
S
S k zk
zC
S
3. Координаты центра тяжести тонкого прямого стержня (вес
пропорционален длине):
lk xk
х
С
L
lk yk
y
C
L
lk zk
zC
L
37

38.

ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
Способы нахождения положения центров
тяжести тел сложной формы:
- Способ симметрии
2
- Способ разбиения
- Способ дополнения
- Способ интегрирования
x C 1 xdV ,
V (V )
y C 1 ydV ,
V (V )
1
1
2
z C 1 zdV .
V (V )
38