Теоретическая механика. Модель 1

1.

Модуль 1.
М
Е
Х
А
Н
И
К
А
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Раздел 1. Статика
Раздел 2. Кинематика
Раздел 3. Динамика точки
Раздел 4. Общие теоремы динамики
Раздел 5. Аналитическая механика

2.

МЕХАНИКА
Теоретическая механика.
Модуль 1
Раздел 1 – СТАТИКА
ВВЕДЕНИЕ В СТАТИКУ
УСЛОВИЯ РАВНОВЕСИЯ
ЦЕНТР ТЯЖЕСТИ
ЛЕКЦИЯ 1
ЛЕКЦИЯ 4
ЛЕКЦИЯ 6
ЛЕКЦИЯ 2
ЛЕКЦИЯ 5
ЛЕКЦИЯ 3

3. ЛЕКЦИЯ 1 План:

МЕХАНИКА
1.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
СТАТИКА
Введение в статику
ЛЕКЦИЯ 1
План:
1.1 Основные понятия и определения.
1.2. Аксиомы статики.
1.3. Связи и их реакции

4. Введение в статику

1.2
Введение в статику
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Статика - раздел механики, в котором излагается
общее учение о силах и условиях равновесия
материальных тел, находящихся под действием сил.
Равновесие - это состояние покоя тела по
отношению к другим телам, например по отношению к
Земле.
Абсолютно твердое тело - такое тело,
расстояние между каждыми двумя точками которого
всегда остается постоянным.

5. Введение в статику

1.3
Введение в статику
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Сила в механике – это величина,
являющаяся основной мерой
механического взаимодействия
материальных тел.
Действие силы на тело
определяется:
линия
действия
силы
- модулем силы;
- направлением вектора силы;
- точкой приложения вектора
силы.
Основная единица измерения силы - 1
ньютон (1 Н).

6. Введение в статику

1.4
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Система сил - совокупность сил, действующих на
рассматриваемое тело
Системы сил
Плоские (линии действия всех сил
лежат в одной плоскости)
Пространственные (линии
действия сил не лежат в
одной плоскости)
Параллельные (линии действия сил параллельны
друг другу)
Произвольные (линии действия сил не пересекаются
и не параллельны)
Сходящиеся (линии действия сил пересекаются
в одной точке)

7. Введение в статику

1.5
Введение в статику
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Эквивалентными называются две системы сил,
приводящие тело к одному и тому же кинематическому
состоянию.
Уравновешенная (эквивалентная нулю) – это такая
система сил, под действием которой свободное твердое
тело может находиться в покое.
Равнодействующей системы сил, называется
сила, эквивалентная данной системе сил.
Сила, приложенная к телу в какой-нибудь одной его точке,
называется сосредоточенной.
Силы, действующие на все точки объема или части
поверхности тела, называются распределенными.

8. Введение в статику

1.6
Введение в статику
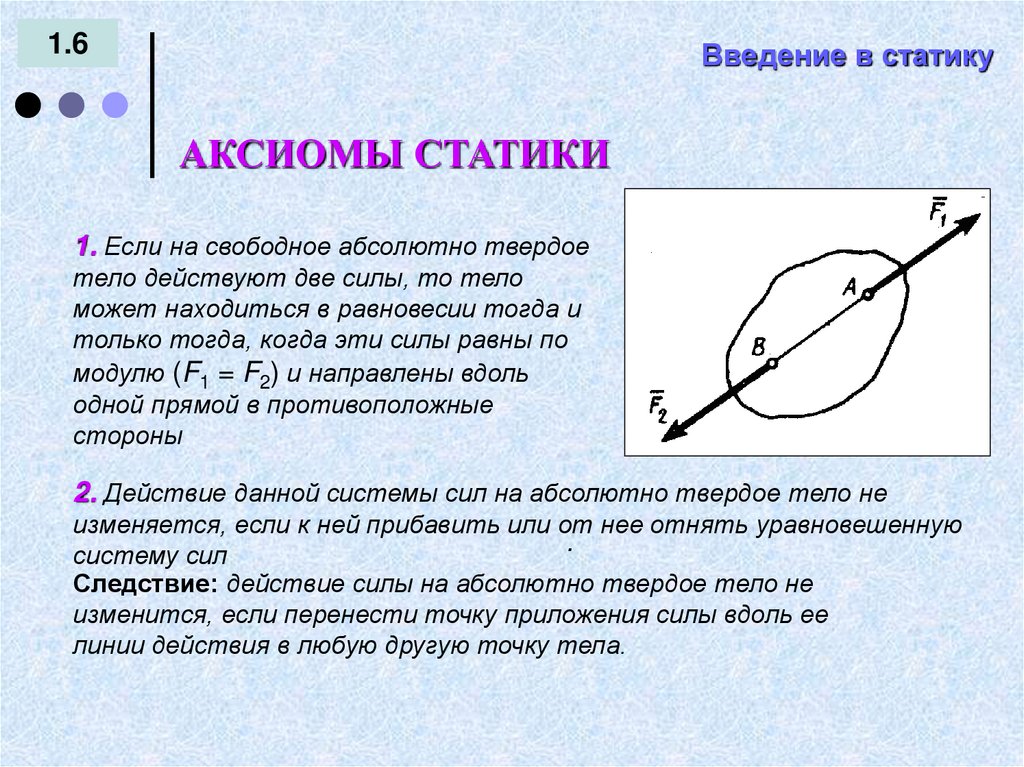
АКСИОМЫ СТАТИКИ
1. Если на свободное абсолютно твердое
тело действуют две силы, то тело
может находиться в равновесии тогда и
только тогда, когда эти силы равны по
модулю (F1 = F2) и направлены вдоль
одной прямой в противоположные
стороны
2. Действие данной системы сил на абсолютно твердое тело не
изменяется, если к ней прибавить или от нее отнять уравновешенную
.
систему сил
Следствие: действие силы на абсолютно твердое тело не
изменится, если перенести точку приложения силы вдоль ее
линии действия в любую другую точку тела.

9. Введение в статику

1.7
Введение в статику
АКСИОМЫ СТАТИКИ
3. Закон параллелограмма сил: две силы, приложенные к телу в
одной точке, имеют равнодействующую, приложенную в той же
точке и изображаемую диагональю параллелограмма,
построенного на этих силах, как на сторонах
R F1 F2

10. Введение в статику

1.8
Введение в статику
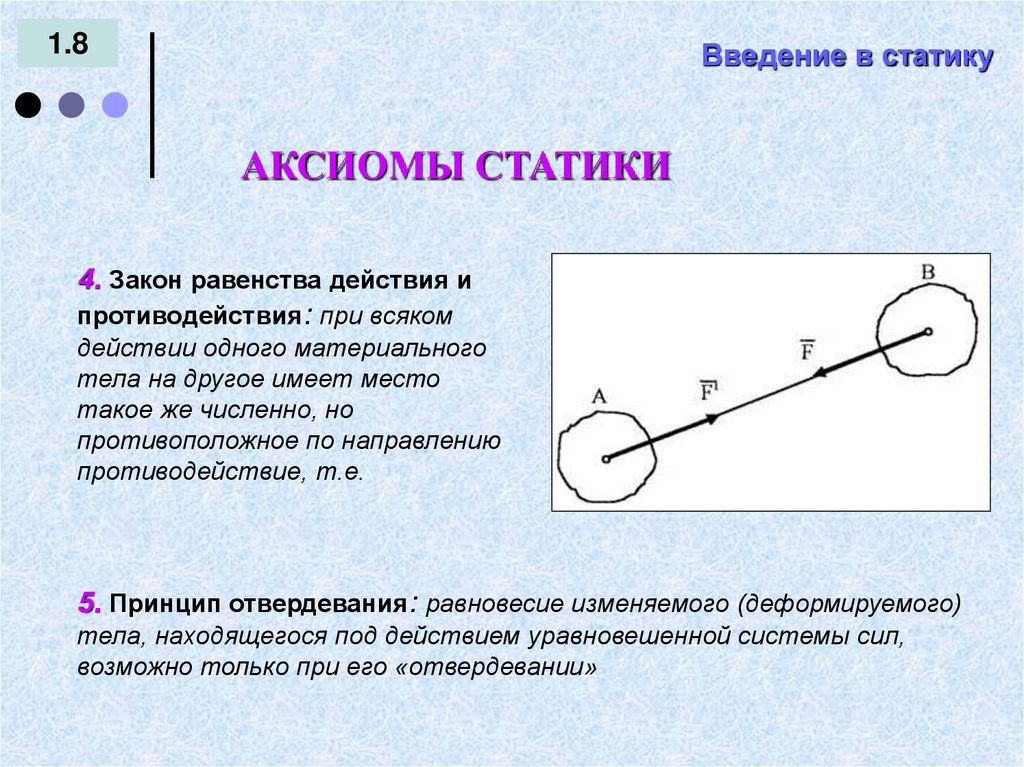
АКСИОМЫ СТАТИКИ
4. Закон равенства действия и
противодействия: при всяком
действии одного материального
тела на другое имеет место
такое же численно, но
противоположное по направлению
противодействие, т.е.
5. Принцип отвердевания: равновесие изменяемого (деформируемого)
тела, находящегося под действием уравновешенной системы сил,
возможно только при его «отвердевании»

11. Введение в статику

1.9
Введение в статику
СВЯЗИ И ИХ РЕАКЦИИ
Свободным называется тело, которое может совершать
из данного положения любые перемещения в пространстве
Несвободным называется тело, перемещениям которого в
пространстве препятствуют какие-нибудь другие, скрепленные
или соприкасающиеся с ним, тела (связи)
Реакция связи – это сила, с которой связь действует на
тело, препятствуя его перемещениям, называется.
Принцип освобождаемости от связей: всякое
несвободное тело можно рассматривать как свободное, если
действие связей заменить их реакциями, приложенными к данному
телу

12. Введение в статику

1.10
Введение в статику
СВЯЗИ И ИХ РЕАКЦИИ
Гладкая
поверхность
Гибкая связь
Шарнирный
стержень

13. Введение в статику

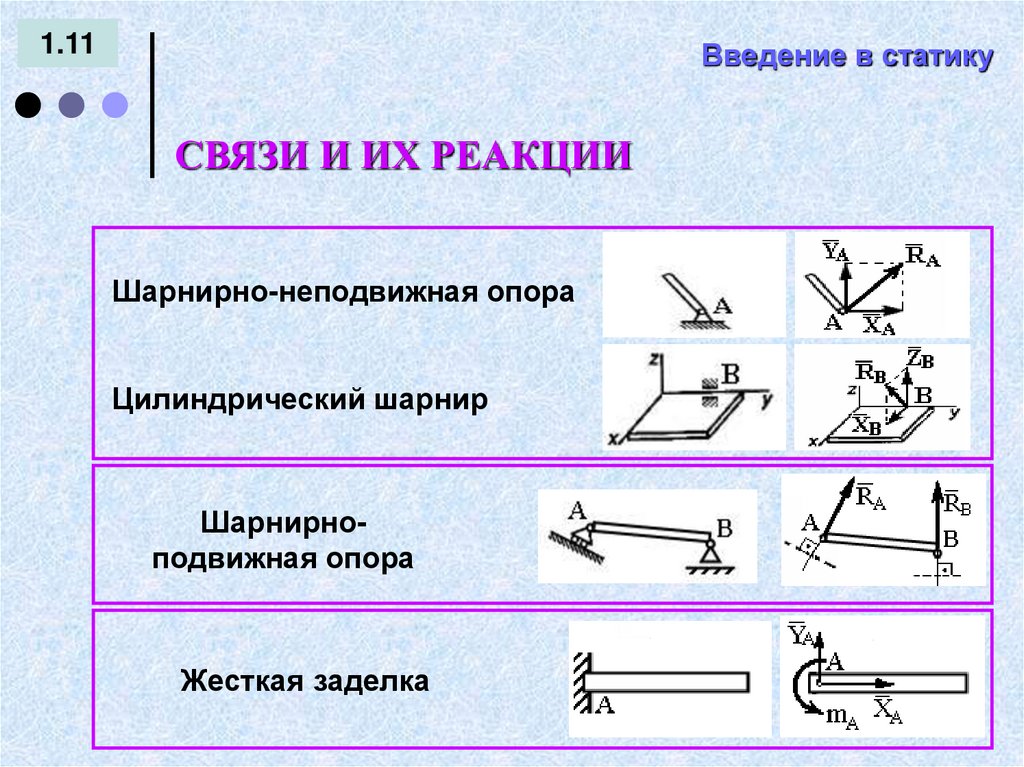
1.11
Введение в статику
СВЯЗИ И ИХ РЕАКЦИИ
Шарнирно-неподвижная опора
Цилиндрический шарнир
Шарнирноподвижная опора
Жесткая заделка

14. ЛЕКЦИЯ 2 План:

МЕХАНИКА
2.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
СТАТИКА
Введение в статику
ЛЕКЦИЯ 2
План:
2.1. Проекции сил.
2.2. Момент силы относительно точки и
относительно оси.
2.3. Пара сил, момент пары

15. Введение в статику

2.2
Введение в статику
ПРОЕКЦИИ СИЛ
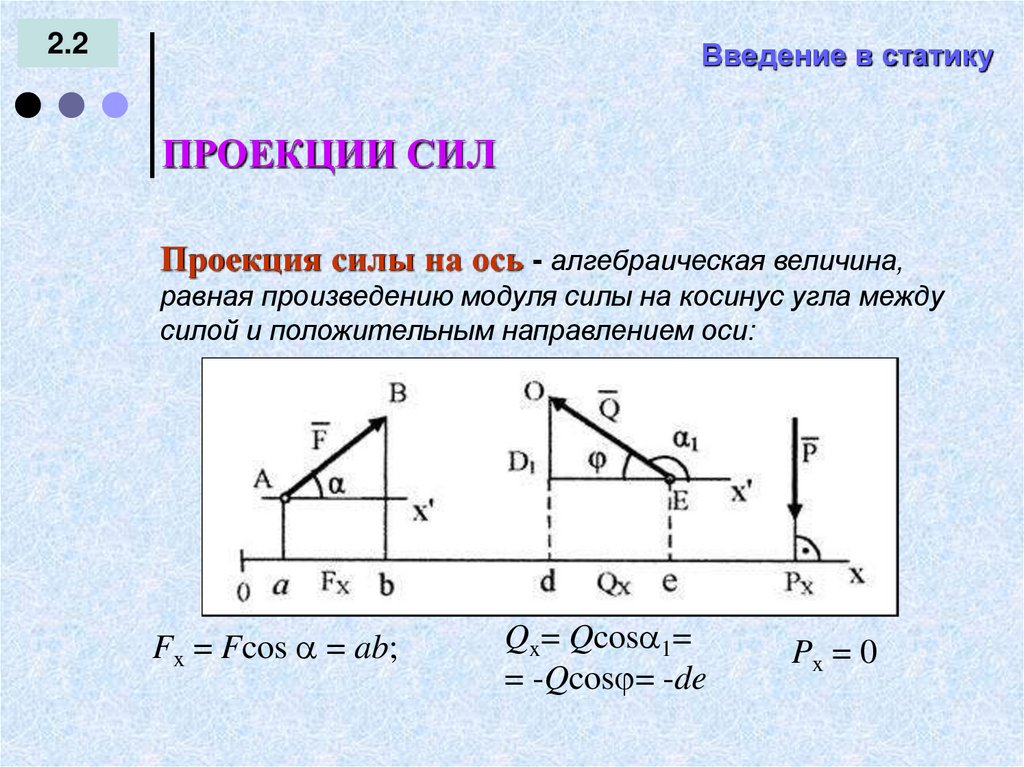
Проекция силы на ось - алгебраическая величина,
равная произведению модуля силы на косинус угла между
силой и положительным направлением оси:
Fx = Fcos = ab;
Qx= Qcos 1=
= -Qcos = -de
Px = 0

16. Введение в статику

2.3
Введение в статику
ПРОЕКЦИИ СИЛ
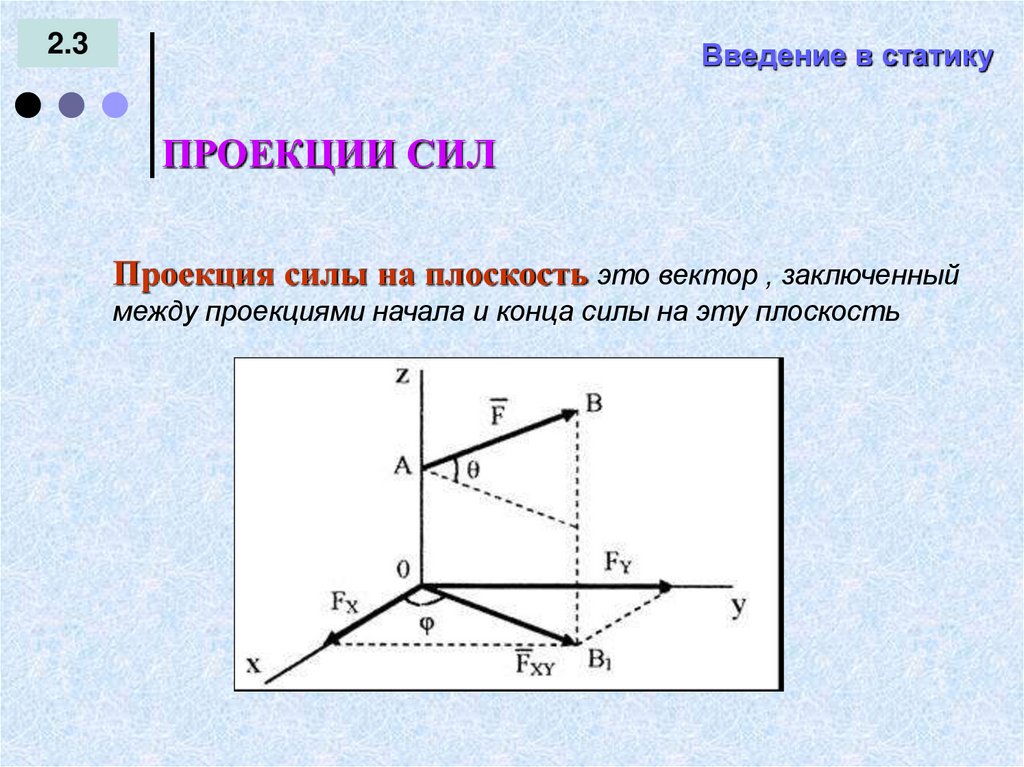
Проекция силы на плоскость это вектор , заключенный
между проекциями начала и конца силы на эту плоскость

17. Введение в статику

2.4
Введение в статику
ПРОЕКЦИИ СИЛ
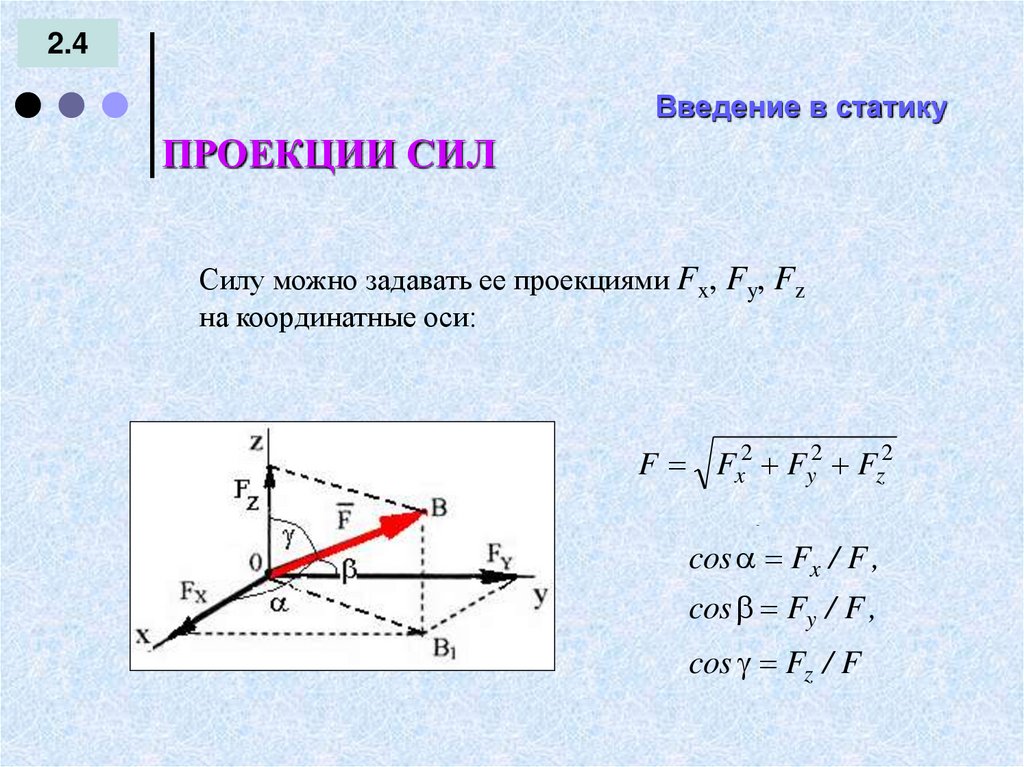
Силу можно задавать ее проекциями Fx, Fy, Fz
на координатные оси:
F Fx2 Fy2 Fz2
F Fx2 Fy2 Fz2
cos Fx / F ,
/ F
Fx, / F ,
cos cos
F
y
/ F
y / F,
cos cos
F
F
z
cos Fz / F

18. Введение в статику

2.5
СПОСОБЫ СЛОЖЕНИЯ И
РАЗЛОЖЕНИЯ СИЛ
Введение в статику
1. Сложение двух сил
Величину, равную геометрической сумме сил системы,
называют главным вектором этой системы сил
R F1 F2
R F12 F22 2F1F2 cos

19. Введение в статику

2.6
Введение в статику
СПОСОБЫ СЛОЖЕНИЯ И
РАЗЛОЖЕНИЯ СИЛ
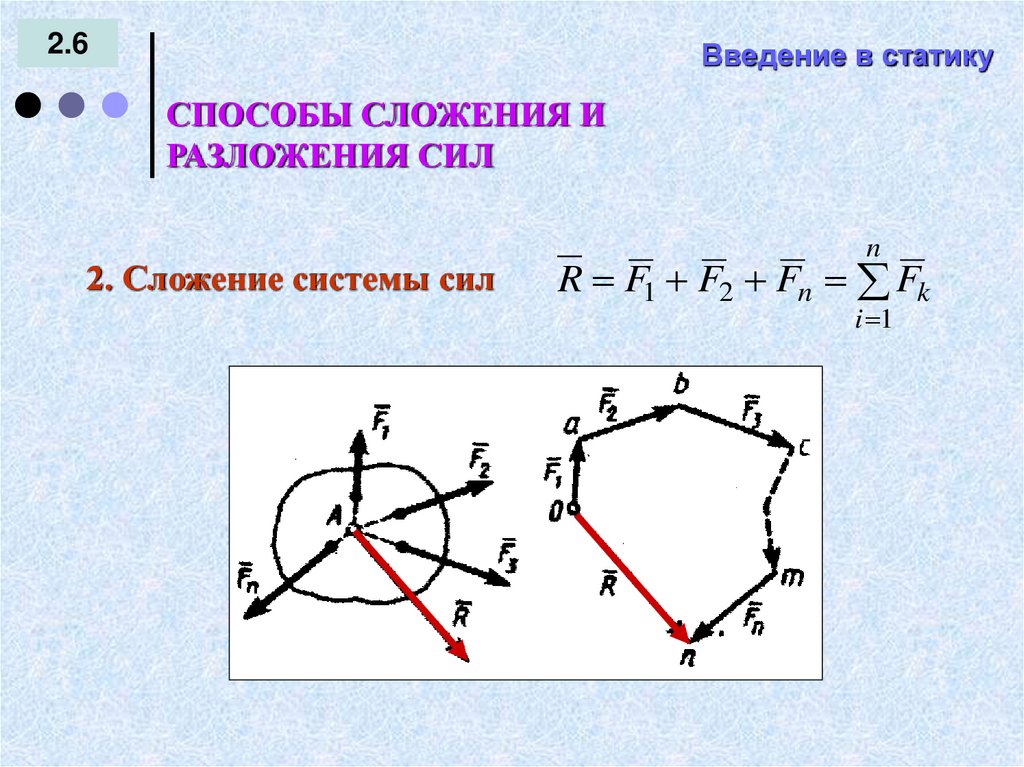
2. Сложение системы сил
n
R F1 F2 Fn Fk
i 1

20. Введение в статику

2.7
Введение в статику
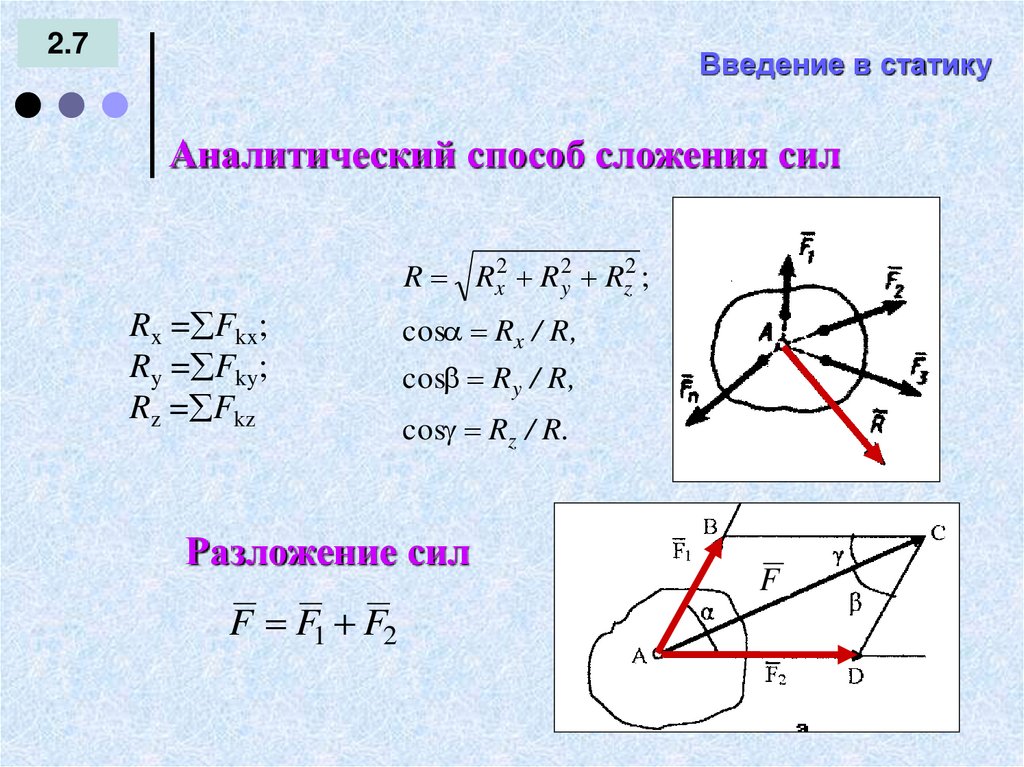
Аналитический способ сложения сил
R Rx2 R y2 Rz2 ;
Rx = Fkx;
Ry = Fky;
Rz = Fkz
cos Rx / R ,
cos Ry / R ,
cos Rz / R.
Разложение сил
F F1 F2
F

21. Введение в статику

2.8
Введение в статику
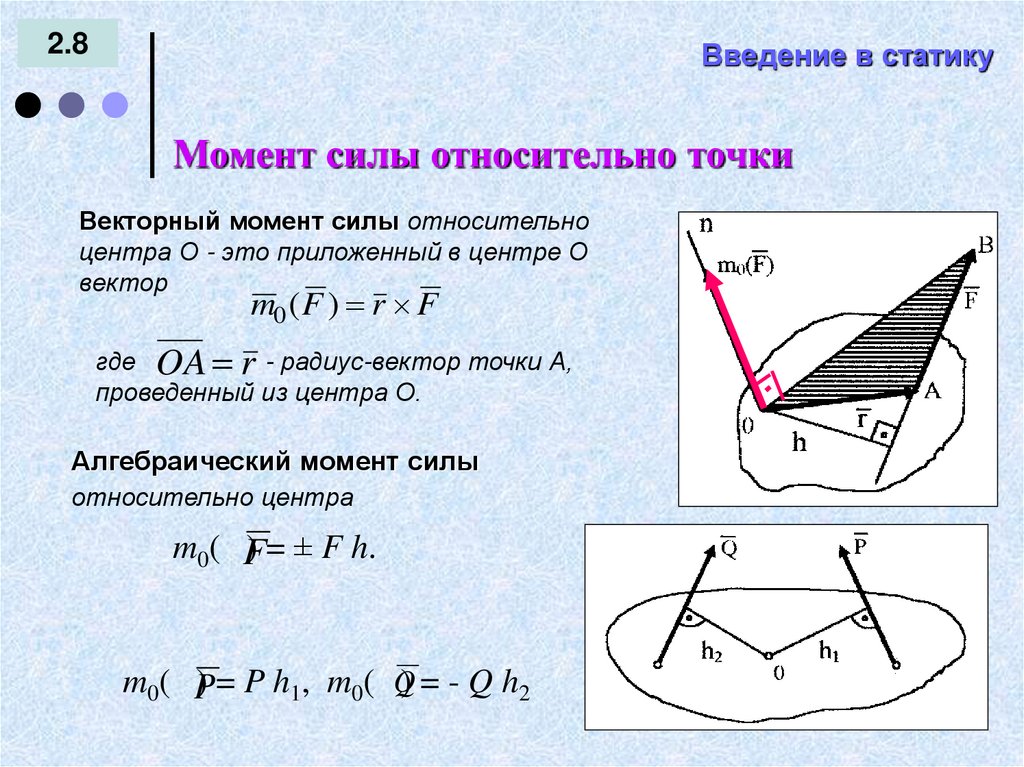
Момент силы относительно точки
Векторный момент силы относительно
центра О - это приложенный в центре О
вектор
m0 ( F ) r F
где OA r - радиус-вектор точки А,
проведенный из центра О.
Алгебраический момент силы
относительно центра
m0( F
) = ± F h.
m0( P
) = P h1, m0( Q) = - Q h2

22. Введение в статику

2.9
Введение в статику
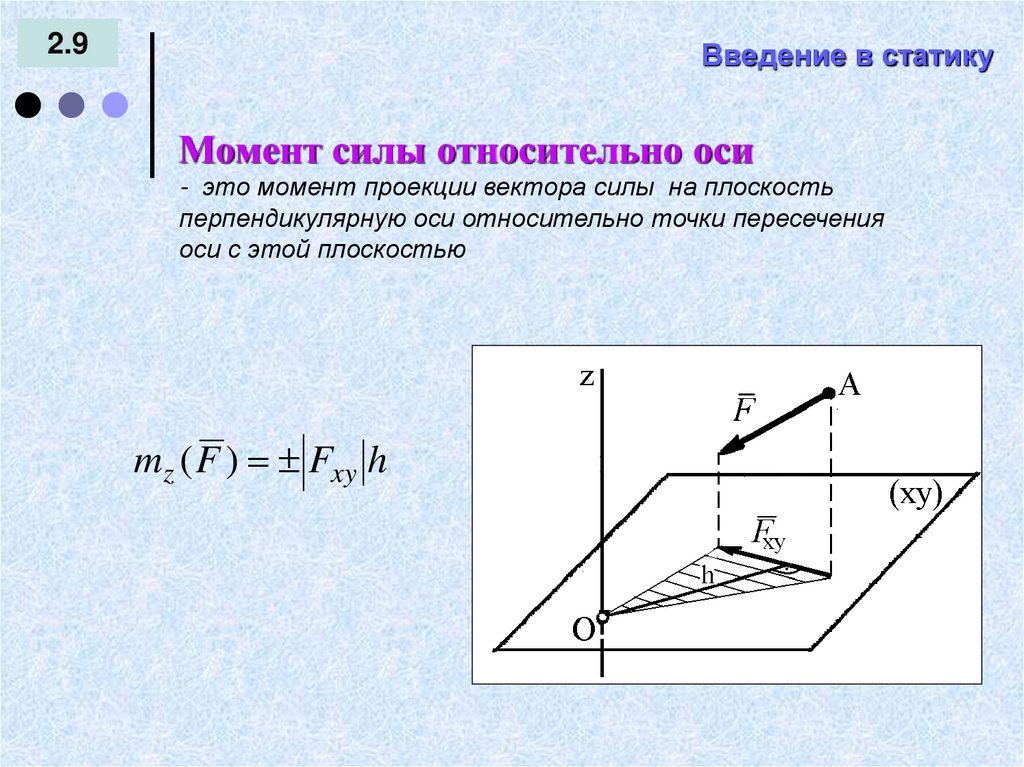
Момент силы относительно оси
- это момент проекции вектора силы на плоскость
перпендикулярную оси относительно точки пересечения
оси с этой плоскостью
mz ( F ) Fxy h

23. Введение в статику

2.10
Введение в статику
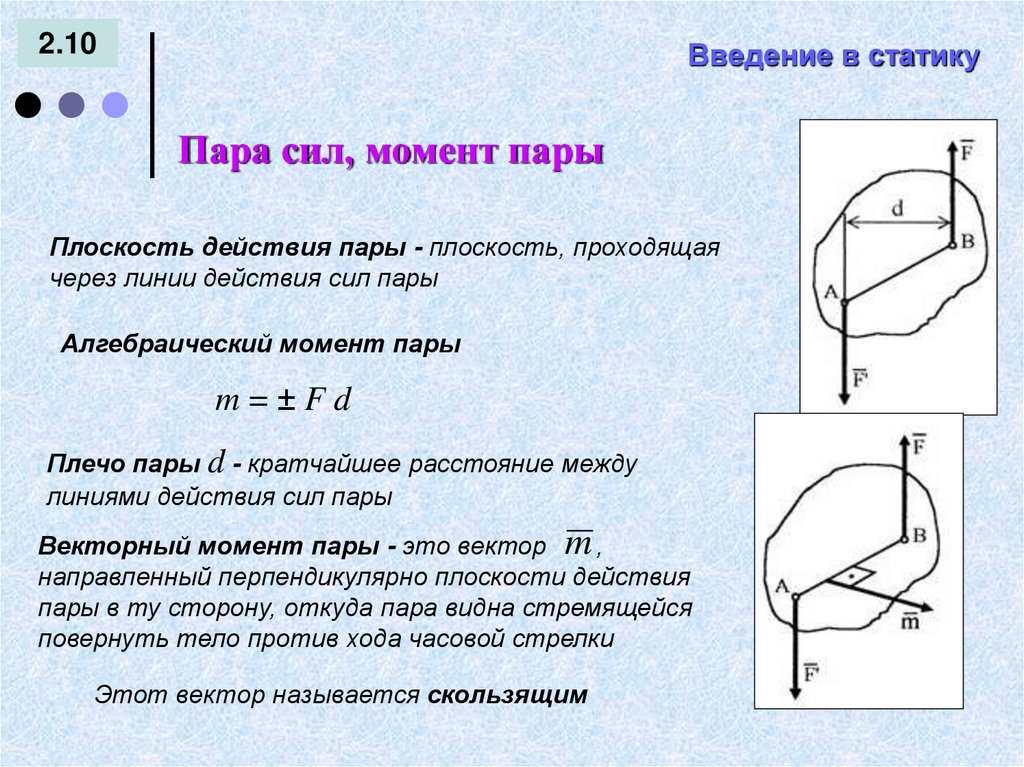
Пара сил, момент пары
Плоскость действия пары - плоскость, проходящая
через линии действия сил пары
Алгебраический момент пары
m=±Fd
Плечо пары d - кратчайшее расстояние между
линиями действия сил пары
Векторный момент пары - это вектор m ,
направленный перпендикулярно плоскости действия
пары в ту сторону, откуда пара видна стремящейся
повернуть тело против хода часовой стрелки
Этот вектор называется скользящим

24. ЛЕКЦИЯ 3 План:

МЕХАНИКА
3.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
СТАТИКА
Введение в статику
ЛЕКЦИЯ 3
План:
3.1. Теорема о параллельном переносе силы.
3.2. Приведение системы сил к центру. Главный
вектор и главный момент системы сил

25. Введение в статику

3.2
Введение в статику
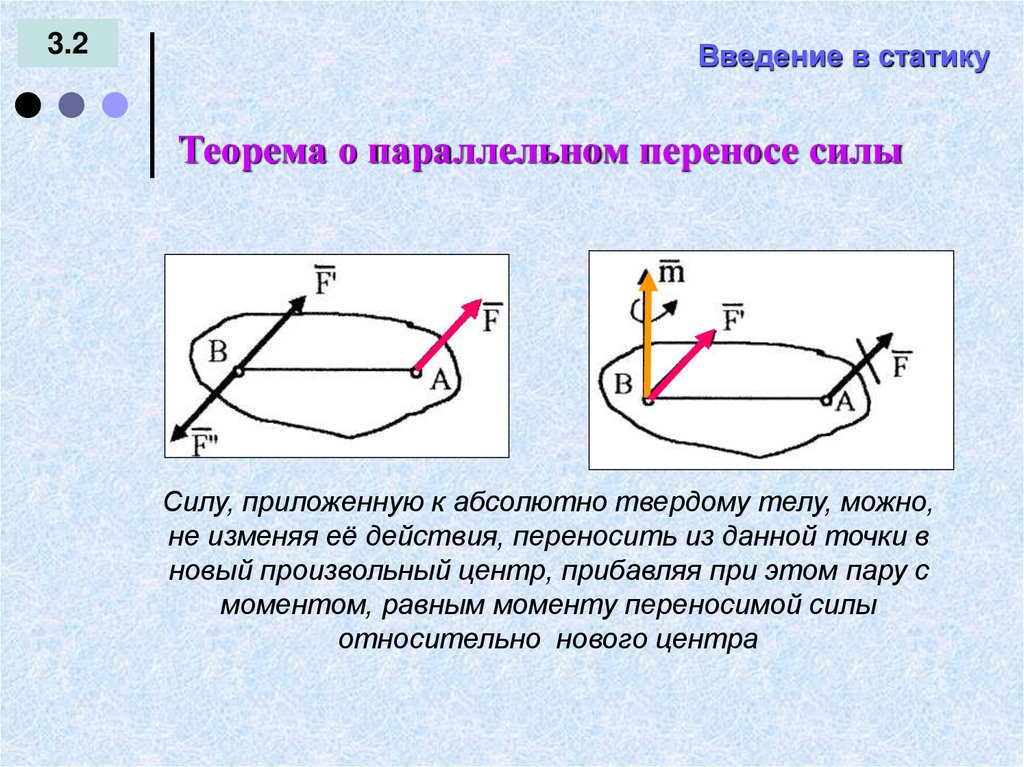
Теорема о параллельном переносе силы
Силу, приложенную к абсолютно твердому телу, можно,
не изменяя её действия, переносить из данной точки в
новый произвольный центр, прибавляя при этом пару с
моментом, равным моменту переносимой силы
относительно нового центра

26. Введение в статику

3.3
Введение в статику
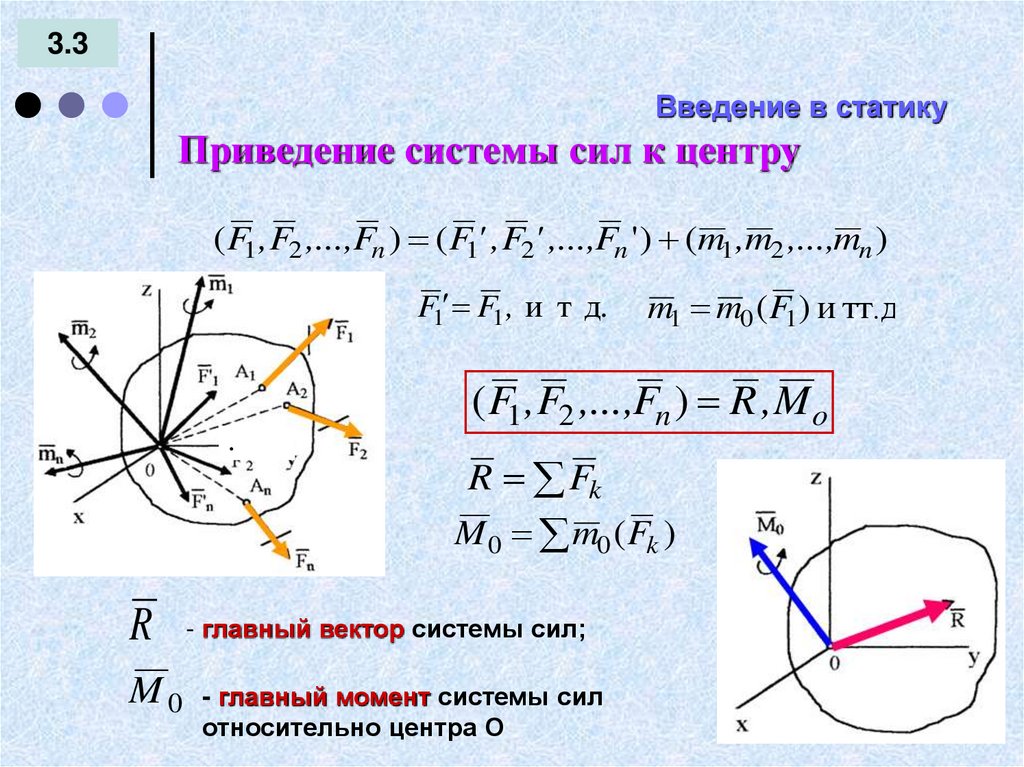
Приведение системы сил к центру
( F1 , F2 ,...,Fn ) ( F1' , F2' ,...,Fn ' ) (m1 ,m2 ,...,mn )
F1 F1 , и т д.
m1 m0 ( F1) и тт.д
( F1 , F2 ,...,Fn ) R ,M o
.
R Fk
M 0 m0 ( Fk )
R - главный вектор системы сил;
M 0 - главный момент системы сил
относительно центра О

27. Введение в статику

3.4
Введение в статику
Приведение системы сил к центру
Частные случаи приведения системы сил к центру:
R 0
данная система сил приводится к одной паре сил
M0 0
R 0
M0 0
данная система сил приводится к одной силе, т. е.
к равнодействующей
R 0
M0 0
данная система сил будет уравновешенной

28. ЛЕКЦИЯ 4 План:

МЕХАНИКА
4.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
СТАТИКА
Условия равновесия
ЛЕКЦИЯ 4
План:
4.1. Теорема Вариньона.
4.2. Условия равновесия различных систем сил.

29.

Условия равновесия
4.2
ТЕОРЕМА ВАРИНЬОНА
Пусть система сил
приводится к
равнодействующей
F1 , F2 ,...,Fn R
Приложим в точке С силу
R R
Система сил F1 , F2 ,...,Fn , R'
будет находиться в равновесии и для нее
M 0 0 или
m0 ( Fk ) m0 ( R ) 0
m0 ( R ) m0 ( R ) mo Fk
Если данная система сил имеет равнодействующую, то момент
равнодействующей относительно любого центра О равен сумме
моментов сил системы относительно того же центра

30.

Условия равновесия
4.3
УСЛОВИЯ РАВНОВЕСИЯ РАЗЛИЧНЫХ
СИСТЕМ СИЛ
Равновесие
пространственной
системы произвольно
расположенных сил
R 0
M0 0
Fkx 0,
Fky 0,
mx ( Fk ) 0,
m y ( Fk ) 0,
Fkz 0,
mz ( Fk ) 0.
Равновесие
пространственной
системы параллельных
сил
Fkx 0,
Fky 0,
mz ( Fk ) 0.
В случае, когда все
действующие на тело силы
параллельны оси z

31.

Условия равновесия
4.4
УСЛОВИЯ РАВНОВЕСИЯ РАЗЛИЧНЫХ
СИСТЕМ СИЛ
Равновесие системы сходящихся сил
R Fk 0
в геометрической форме: необходимо и
достаточно, чтобы силовой многоугольник,
построенный из векторов сил, был замкнутым
в аналитической форме:
R Rx2 Ry2 Rz2 0, или
Rx = 0, Ry = 0, Rz = 0,
Fkx 0, Fky 0, Fkz 0

32.

4.5
Условия равновесия
УСЛОВИЯ РАВНОВЕСИЯ РАЗЛИЧНЫХ
СИСТЕМ СИЛ
Равновесие плоской системы произвольных сил
2
1
Fkx 0,
Fky 0,
m0 ( Fk ) 0
3
m A ( Fk ) 0,
mB ( Fk ) 0,
Fkx 0
ось Ох, не
перпендикулярна
прямой АВ
m A ( Fk ) 0,
mB ( Fk ) 0,
mC ( Fk ) 0
центры А, В и С,
не лежат
на одной прямой

33.

4.6
Условия равновесия
УСЛОВИЯ РАВНОВЕСИЯ РАЗЛИЧНЫХ
СИСТЕМ СИЛ
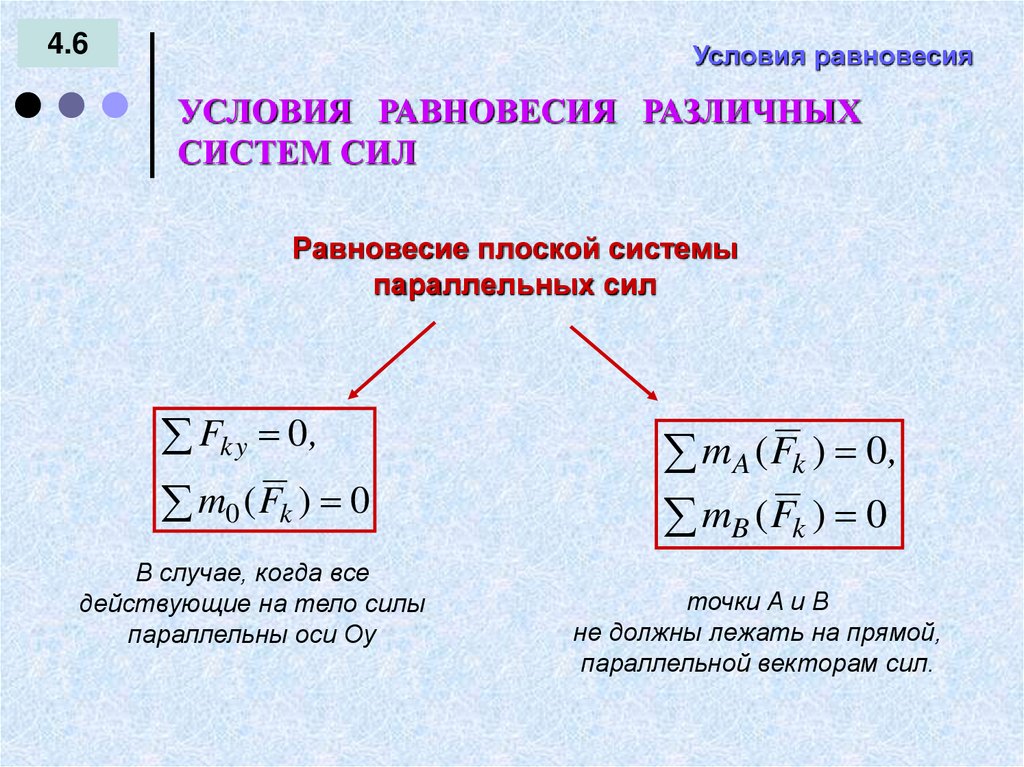
Равновесие плоской системы
параллельных сил
Fky 0 ,
m0 ( Fk ) 0
В случае, когда все
действующие на тело силы
параллельны оси Оу
m A ( Fk ) 0,
mB ( Fk ) 0
точки A и В
не должны лежать на прямой,
параллельной векторам сил.

34. ЛЕКЦИЯ 5 План:

МЕХАНИКА
5.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
СТАТИКА
Условия равновесия
ЛЕКЦИЯ 5
План:
5.1. Равновесие систем тел.
5.2. Равновесие тела при наличии трения

35.

5.2
Условия равновесия
РАВНОВЕСИЕ СИСТЕМ ТЕЛ
Внутренние связи – это связи, соединяющие части конструкции
Два способа решения задач
на равновесие составной конструкции:
1 способ. Рассматривают равновесие всей конструкции как единое
целое (не учитывая реакции внутренних связей) и дополнительно
равновесие какой-нибудь одной или нескольких частей конструкции
с учетом реакций внутренних связей.
2 способ. Конструкцию расчленяют на части и рассматривают
равновесие каждой части, учитывая при этом реакции внутренних
связей. При этом реакции внутренних связей будут попарно равны
по модулю и противоположны по направлению.

36.

Условия равновесия
5.3
РАВНОВЕСИЕ ТЕЛ ПРИ
НАЛИЧИИ ТРЕНИЯ
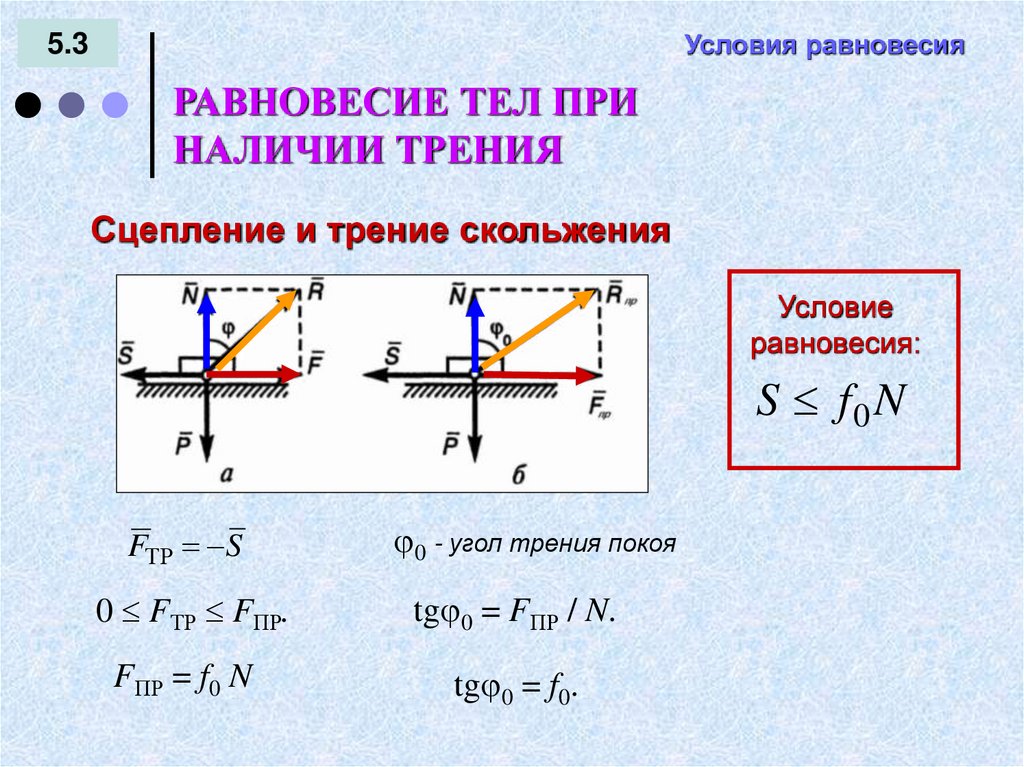
Сцепление и трение скольжения
Условие
равновесия:
S f0 N
FТР S
0 - угол трения покоя
0 FТР FПР.
tg 0 = FПР / N.
FПР = f0 N
tg 0 = f0.

37.

Условия равновесия
5.4
РАВНОВЕСИЕ ТЕЛ ПРИ
НАЛИЧИИ ТРЕНИЯ
Трение качения
mA ( Fk ) 0
N QПР R 0
QПР = ( /R) N.
Условие равновесия:
Q N
R
( Q , F ) – пара сил
( N
P ) – пара сил
Q f0 N

38. ЛЕКЦИЯ 5 План:

МЕХАНИКА
6.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
СТАТИКА
ЦЕНТР ТЯЖЕСТИ
ЛЕКЦИЯ 5
План:
6.1. Центр параллельных сил
6.2. Центр тяжести твердого тела

39.

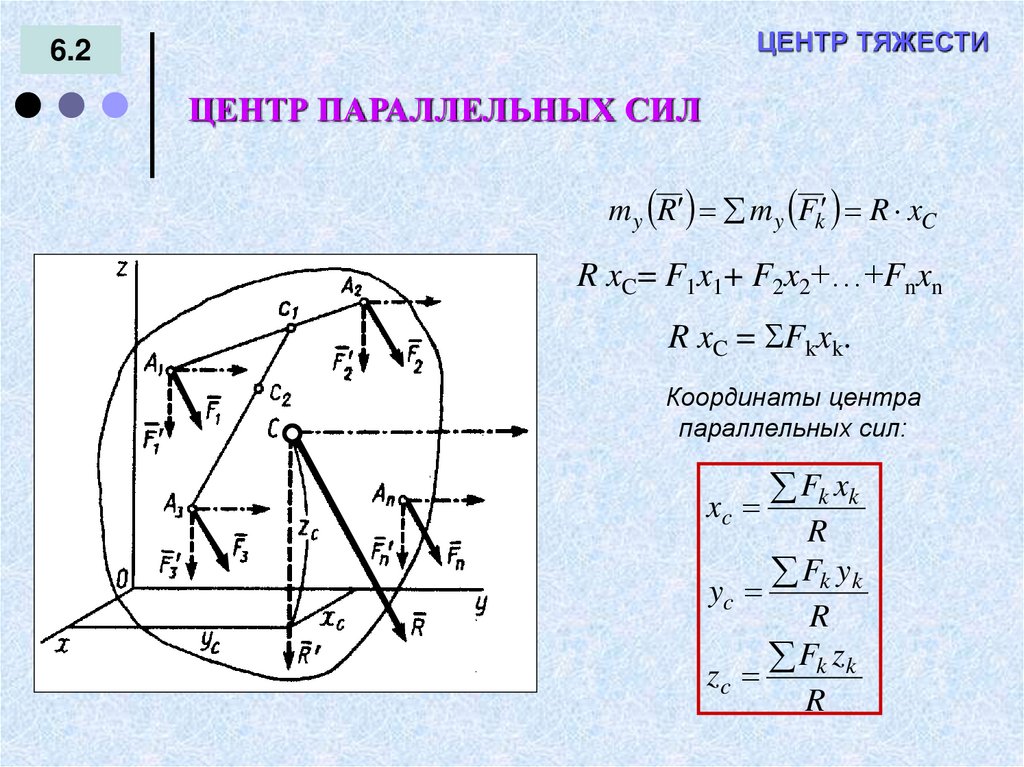
ЦЕНТР ТЯЖЕСТИ
6.2
ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
m y R m y Fk R xC
R xC= F1x1+ F2x2+…+Fnxn
R xC = Fkxk.
Координаты центра
параллельных сил:
xc
Fk xk
R
Fk yk
yc
R
Fk zk
zc
R

40.

ЦЕНТР ТЯЖЕСТИ
6.3
ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
Силовое поле – это область, в которой на
каждую материальную точку действует сила,
зависящая от положения этой точки,
Поле тяжести вблизи земной поверхности
можно назвать однородным полем тяжести.
Модуль равнодействующей сил тяжести
называется весом тела Р
Координаты центра тяжести:
хС
рk xk
Р
yC
рk yk
Р
zC
рk zk
Р

41.

ЦЕНТР ТЯЖЕСТИ
6.4
ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
Центр тяжести некоторых однородных тел
1 Для однородного объемного твердого тела (вес пропорционален
объему):
V x
х k k
С
V
V y
y k k
C
V
Vk zk
z
C
V
2. Для тела, представляющего собой однородную пластину (вес
пропорционален площади):
Sk xk
х
С
S
S k yk
y
C
S
S k zk
zC
S
3. Координаты центра тяжести тонкого прямого стержня (вес
пропорционален длине):
lk xk
х
С
L
lk yk
y
C
L
lk zk
zC
L

42.

ЦЕНТР ТЯЖЕСТИ
6.4
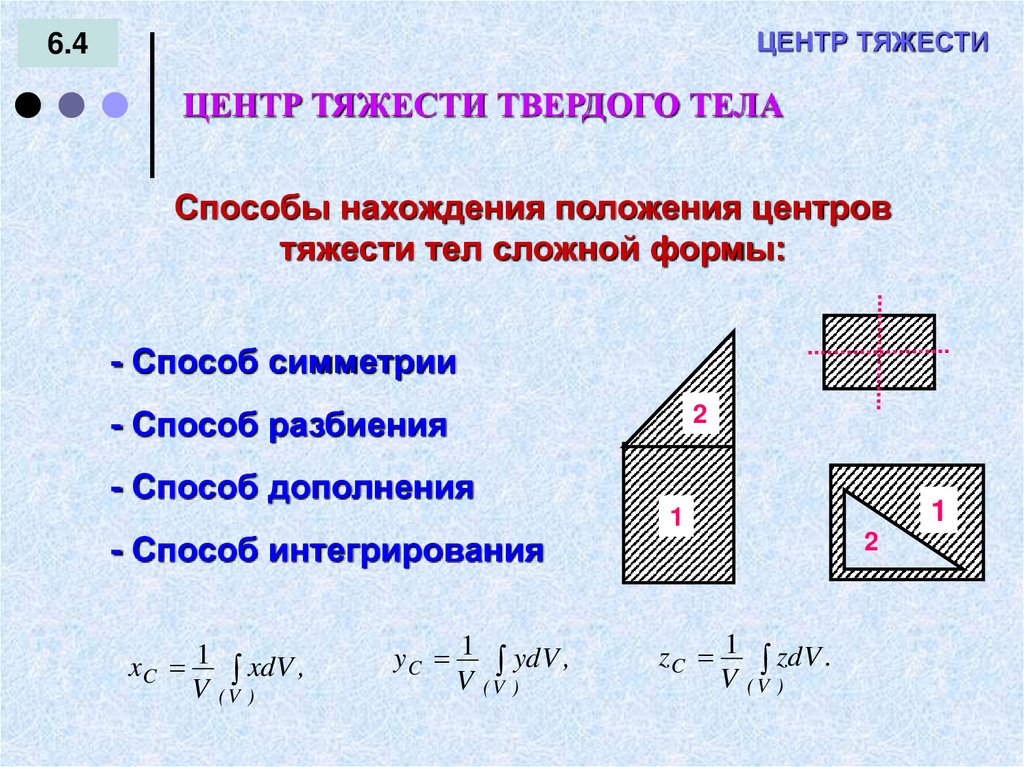
ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
Способы нахождения положения центров
тяжести тел сложной формы:
- Способ симметрии
2
- Способ разбиения
- Способ дополнения
- Способ интегрирования
x C 1 xdV ,
V (V )
y C 1 ydV ,
V (V )
1
1
2
z C 1 zdV .
V (V )

43.

МЕХАНИКА
Теоретическая механика
Модуль 1
Раздел 2 – КИНЕМАТИКА
КИНЕМАТИКА ТОЧКИ
КИНЕМАТИКА ТВЕРДОГО
ТЕЛА
СЛОЖНОЕ ДВИЖЕИЕ ТОЧКИ
ПЛОСКОПАРАЛЛЕЛЬНОЕ
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
ЛЕКЦИЯ 7
ЛЕКЦИЯ 8
ЛЕКЦИЯ 9
ЛЕКЦИЯ 10
ЛЕКЦИЯ 11
ЛЕКЦИЯ 12
ЛЕКЦИЯ 13

44. ЛЕКЦИЯ 7 План:

МЕХАНИКА
7.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
КИНЕМАТИКА
Кинематика точки
ЛЕКЦИЯ 7
План:
7.1. Векторный способ задания движения точки.
7.2. Координатный способ задания движения

45.

7.2
КИНЕМАТИКА ТОЧКИ
Кинематикой
называется раздел механики, в котором
изучаются геометрические свойства движения тел без учета их
инертности и действующих на них сил.
Траекторией точки называется непрерывная линия,
которую описывает движущаяся точка относительно данной
системы отсчета.
Для задания движения точки можно применять способы:
- векторный;
- координатный;
- естественный.

46.

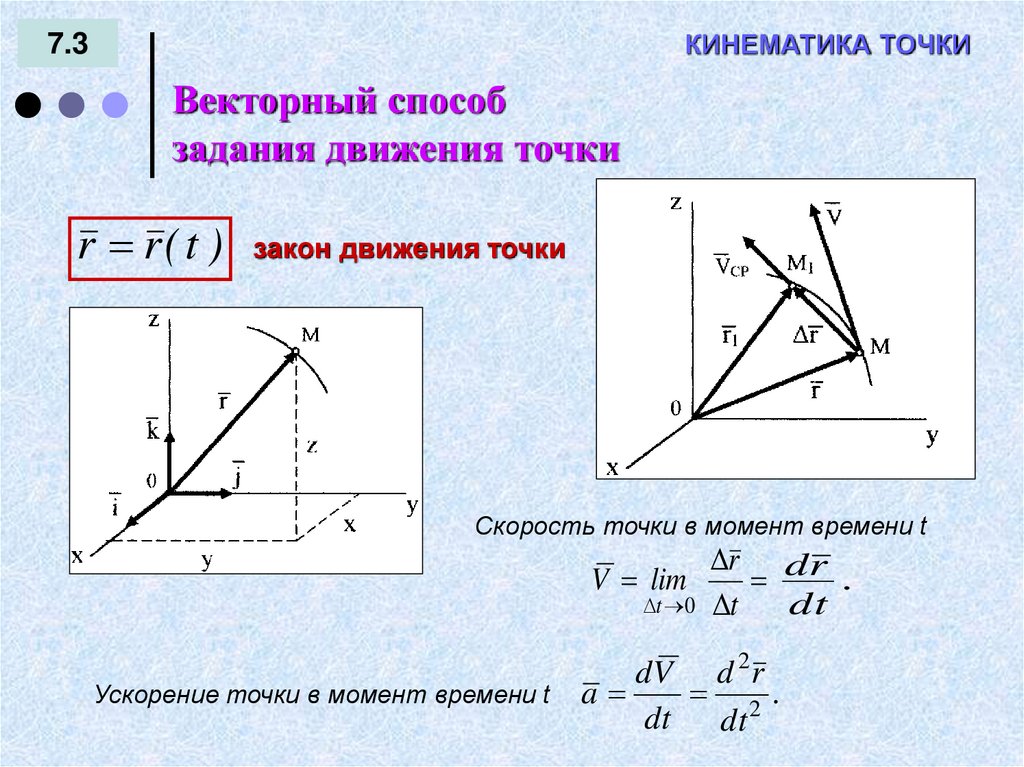
КИНЕМАТИКА ТОЧКИ
7.3
Векторный способ
задания движения точки
r r ( t ) закон движения точки
Скорость точки в момент времени t
r dr
.
t 0 t
dt
V lim
Ускорение точки в момент времени t
dV d 2 r
a
2.
dt
dt

47.

КИНЕМАТИКА ТОЧКИ
7.4
Координатный способ
задания движения точки
x = f1(t);
у = f2(t); закон движения точки
z = f3(t).
ускорение точки
скорость точки
dx
vx = dt
dy
vy =
dt
dz
vz = dt
v vx2 v 2y vz2
cos vx / v
cos v y / v
cos vz / v.
dv x d 2 x
,
2
dt dt
a a x2 a 2y a z2
dv y
d2y
ay
,
2
dt
dt
cos 1 a x / a ,
dv z d 2 z
az
,
2
dt dt
cos 1 a z / a .
ax
cos 1 a y / a ,

48. ЛЕКЦИЯ 8 План:

МЕХАНИКА
8.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
КИНЕМАТИКА
Кинематика точки
ЛЕКЦИЯ 8
План:
8.1. Естественный способ задания движения точки.
8.2. Частные случаи движения точки

49.

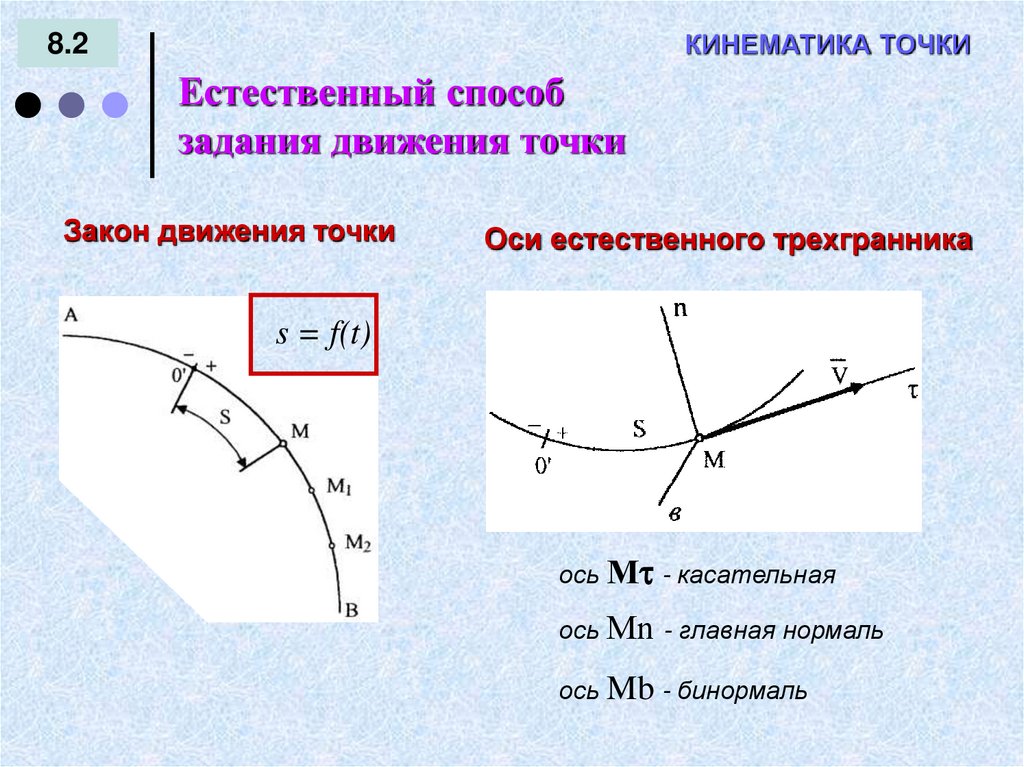
КИНЕМАТИКА ТОЧКИ
8.2
Естественный способ
задания движения точки
Закон движения точки
Оси естественного трехгранника
s = f(t)
ось М - касательная
ось Мn - главная нормаль
ось Mb - бинормаль

50.

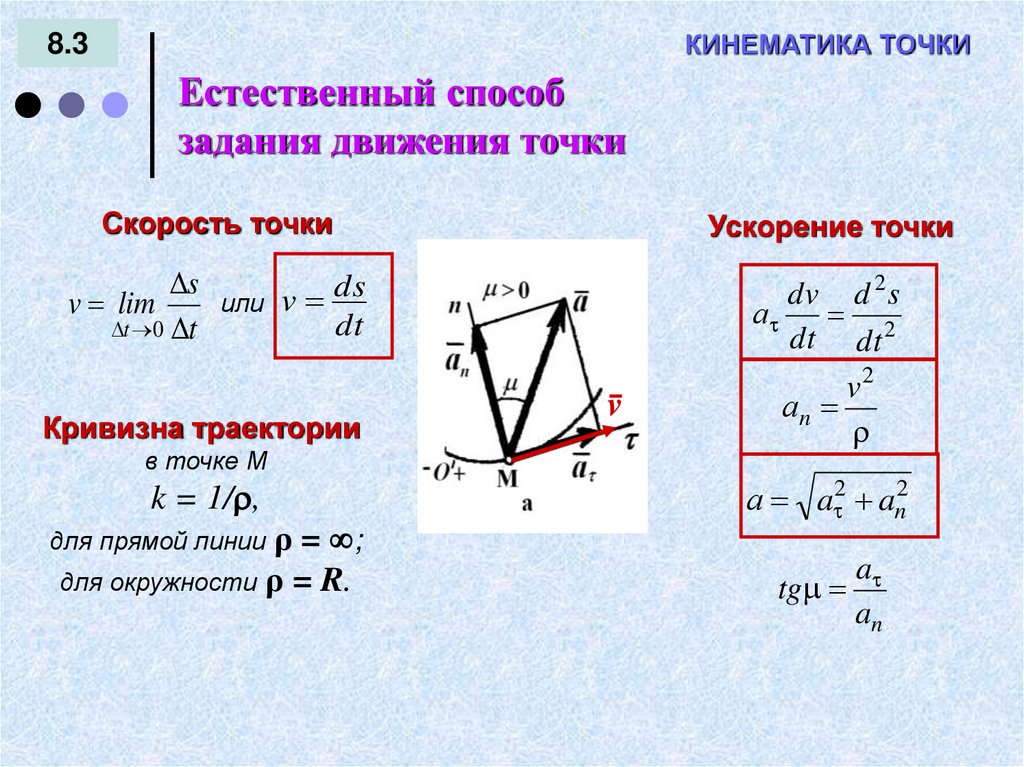
КИНЕМАТИКА ТОЧКИ
8.3
Естественный способ
задания движения точки
Скорость точки
Ускорение точки
s
ds
или v
v lim
dt
t 0 t
dv d 2 s
а
2
dt dt
Кривизна траектории
v2
аn
в точке М
v
k = 1/ ,
а a 2 an2
для окружности ρ = R.
a
tg
an
для прямой линии ρ = ;

51.

КИНЕМАТИКА ТОЧКИ
8.4
Естественный способ
задания движения точки
Частные случаи движения точки
Прямолинейное
движение
=
Тогда
an = v2 / = 0
Полное ускорение :
a = a = dv/dt.
При равномерном
движении
v = const, a = 0,
а=0
Криволинейное
движение
- равномерное движение
v = const
a = dv/dt = 0
a = an = v2/ .
- равнопеременное движение
a = const
an = v2/ .
а a 2 an2

52. ЛЕКЦИЯ 9 План:

МЕХАНИКА
9.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
КИНЕМАТИКА
Кинематика твердого тела.
Простейшие движения
ЛЕКЦИЯ 9
План:
9.1. Поступательное движение тела.
9.2. Вращение твёрдого тела вокруг неподвижной оси.

53.

9.2
Простейшие движения твердого тела
Поступательное движение тела
Поступательным называется движение
твердого тела, при котором любая
прямая, проведенная в этом теле,
перемещается, оставаясь параллельной
своему начальному направлению.
Свойства поступательного
движения:
1.
Все точки тела описывают одинаковые траектории
2. Все точки тела имеют в каждый момент времени одинаковые по
модулю и направлению скорости и ускорения

54.

Простейшие движения твердого тела
9.3
ВРАЩЕНИЕ ТВЁРДОГО ТЕЛА
ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Вращательным движением твердого тела
вокруг неподвижной оси называется
движение, при котором какие-нибудь две
точки, принадлежащие телу (или неизменно
с ним связанные), остаются во все время
движения неподвижными
Проходящая через неподвижные точки
прямая - ось вращения.
=
f(t)
φ - угол поворота тела
закон вращательного движения
твердого тела вокруг неподвижной оси.

55.

Простейшие движения твердого тела
9.4
ВРАЩЕНИЕ ТВЁРДОГО ТЕЛА
ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Угловая скорость тела
d
dt
Единица измерения
рад/с, 1/с, с-1.
Угловое ускорение тела
d d 2
2
dt dt
Единица измерения ε
рад/с2,
1/с2 ,
с-2.

56.

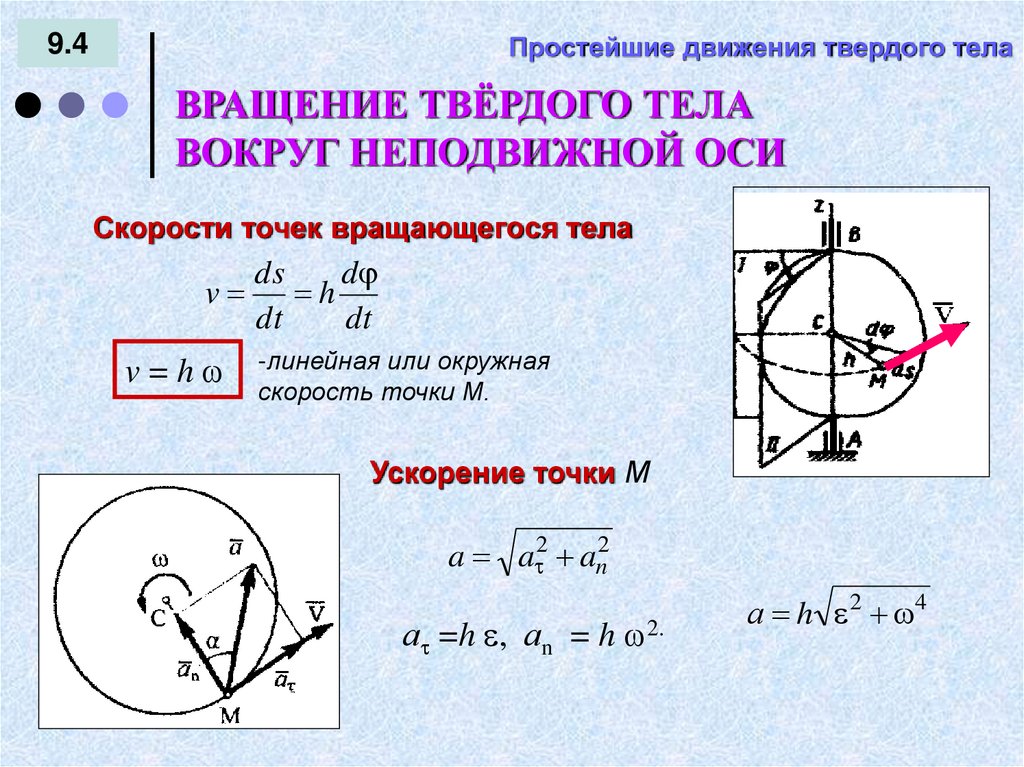
Простейшие движения твердого тела
9.4
ВРАЩЕНИЕ ТВЁРДОГО ТЕЛА
ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Скорости точек вращающегося тела
ds
d
v h
dt
dt
v=h
-линейная или окружная
скорость точки М.
Ускорение точки М
a a 2 an2
а =h , аn = h 2.
а h 2 4

57. ЛЕКЦИЯ 10 План:

МЕХАНИКА
10.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
КИНЕМАТИКА
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
ЛЕКЦИЯ 10
План:
10.1. Основные определения.
10.2. Теорема о сложении скоростей (теорема Кориолиса).

58.

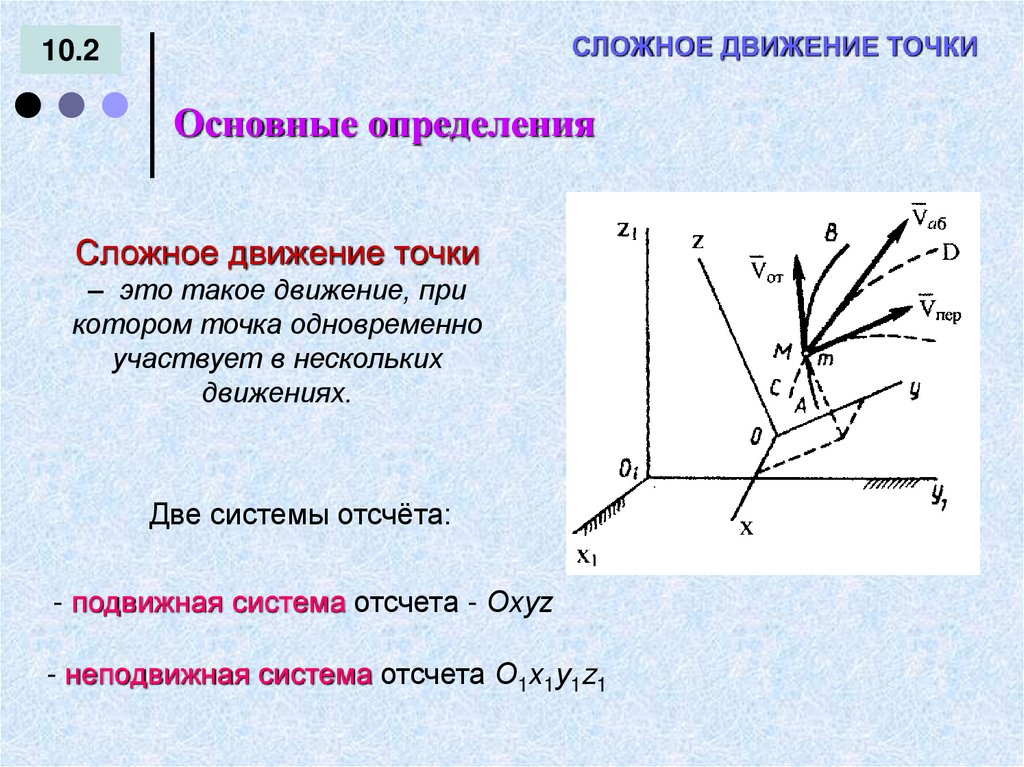
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
10.2
Основные определения
Сложное движение точки
– это такое движение, при
котором точка одновременно
участвует в нескольких
движениях.
Две системы отсчёта:
- подвижная система отсчета - Охуz
- неподвижная система отсчета О1х1у1z1

59.

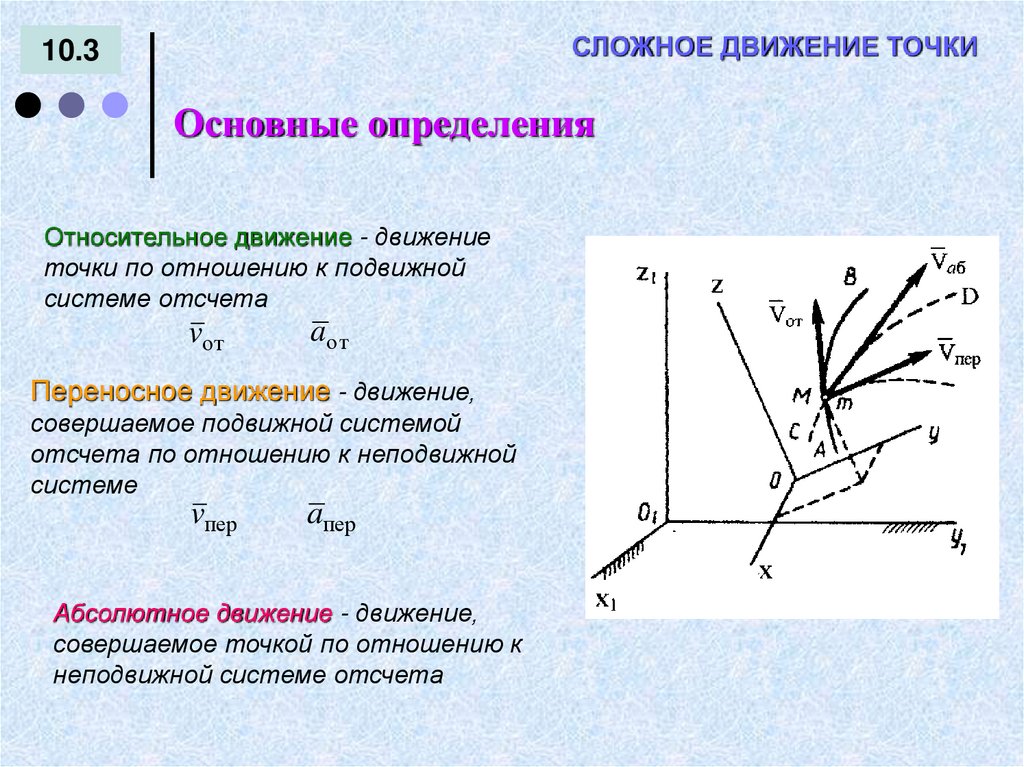
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
10.3
Основные определения
Относительное движение - движение
точки по отношению к подвижной
системе отсчета
vот
aот
Переносное движение - движение,
совершаемое подвижной системой
отсчета по отношению к неподвижной
системе
vпер
aпер
Абсолютное движение - движение,
совершаемое точкой по отношению к
неподвижной системе отсчета

60.

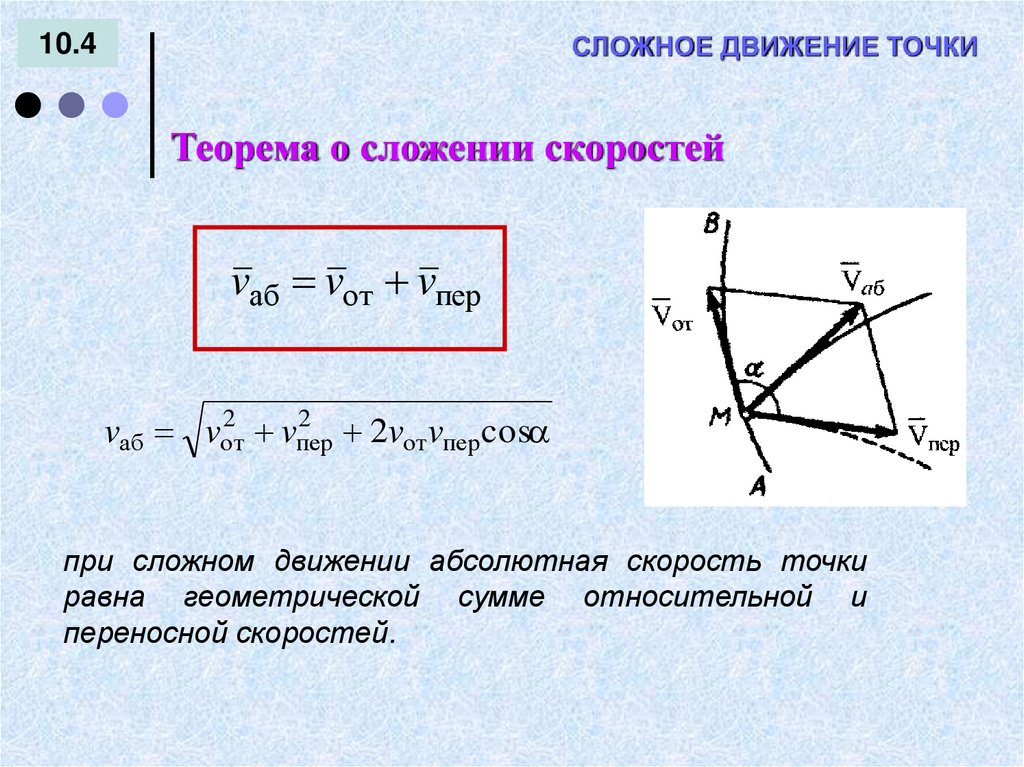
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
10.4
Теорема о сложении скоростей
vаб vот vпер
2
2
vаб vот
vпер
2vотvперcos
при сложном движении абсолютная скорость точки
равна геометрической сумме относительной и
переносной скоростей.

61. ЛЕКЦИЯ 8 План:

МЕХАНИКА
11.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
КИНЕМАТИКА
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
ЛЕКЦИЯ 8
План:
11.1. Теорема о сложении ускорений.
11.2. Ускорение Кориолиса.

62.

СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
11.2
ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ
(ТЕОРЕМА КОРИОЛИСА)
dvаб dvот dvпер
aаб
dt
dt
dt
aаб
(dvот )от (dvот )пер (dvпер )от (dvпер )пер
dt
dt
dt
dt
aаб aот aпер aкор
акор
(dvпер )от
dt
(dvпер )пер
dt
- кориолисово ускорение
(ускорение Кориолиса)

63.

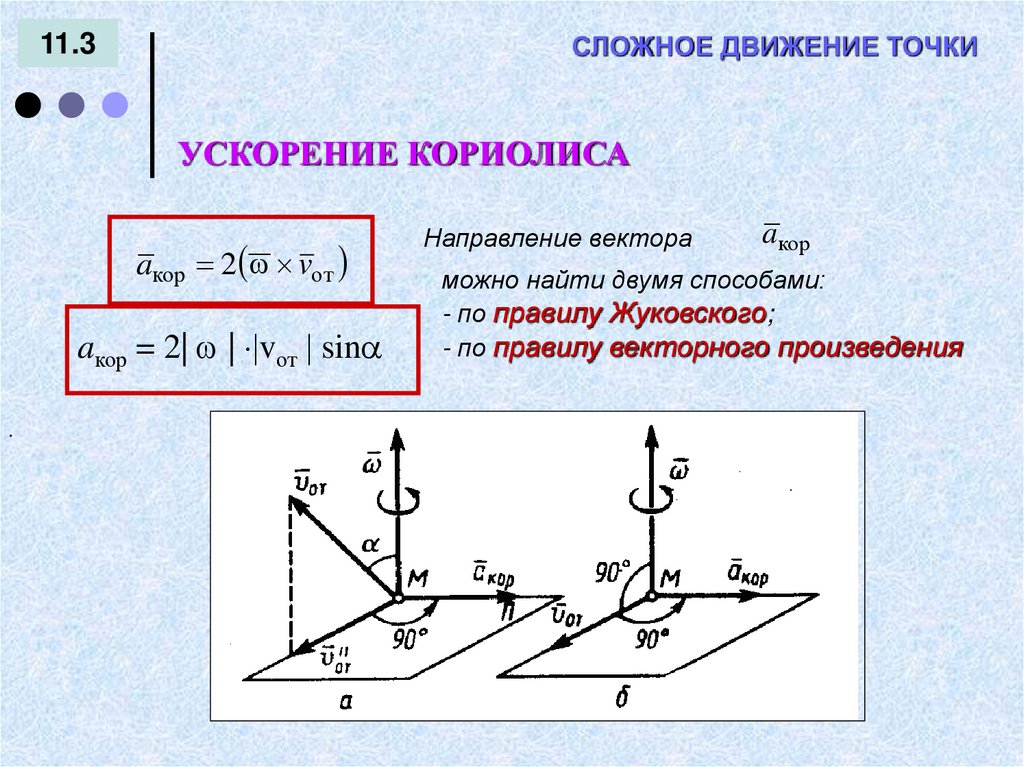
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
11.3
УСКОРЕНИЕ КОРИОЛИСА
aкор 2 vот
aкор = 2| | vот sin
.
Направление вектора
aкор
можно найти двумя способами:
- по правилу Жуковского;
- по правилу векторного произведения

64.

СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
11.4
УСКОРЕНИЕ КОРИОЛИСА
aкор 0
aкор 2 vот
в следующих случаях:
- когда = 0, т. е. переносное движение является поступательным;
- когда относительная скорость в данный момент времени
обращается в нуль;
- когда угол между векторами
когда
и vот = 0, или = 180°, т.е.
vот параллелен оси переносного вращения

65. ЛЕКЦИЯ 12 План:

МЕХАНИКА
12.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
КИНЕМАТИКА
Плоскопараллельное движение
твердого тела
ЛЕКЦИЯ 12
План:
12.1. Понятие плоскопараллельного движения тела
12.2. Определение скоростей точек плоской фигуры
12.3. Понятие МЦС и способы его нахождения

66.

12.2
Плоскопараллельное движение твердого тела
Понятие о плоскопараллельном
движении тела
Плоскопараллельное (плоское) движение
- такое движение твердого тела, при
котором все его точки перемещаются
параллельно некоторой фиксированной
плоскости П
Закон движения плоской фигуры:
полюс
xA = f1(t);
уA = f2(t);
= f3(t)

67.

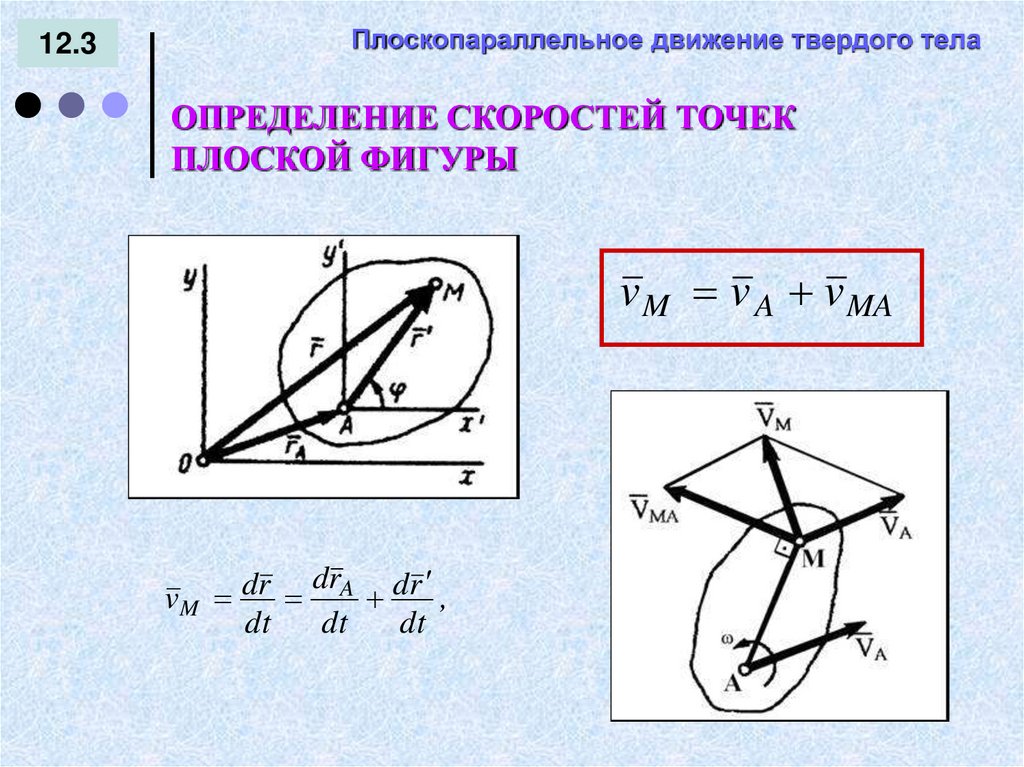
12.3
Плоскопараллельное движение твердого тела
ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК
ПЛОСКОЙ ФИГУРЫ
v M v A v MA
dr
vM dr A dr ,
dt
dt
dt

68.

12.4
Плоскопараллельное движение твердого тела
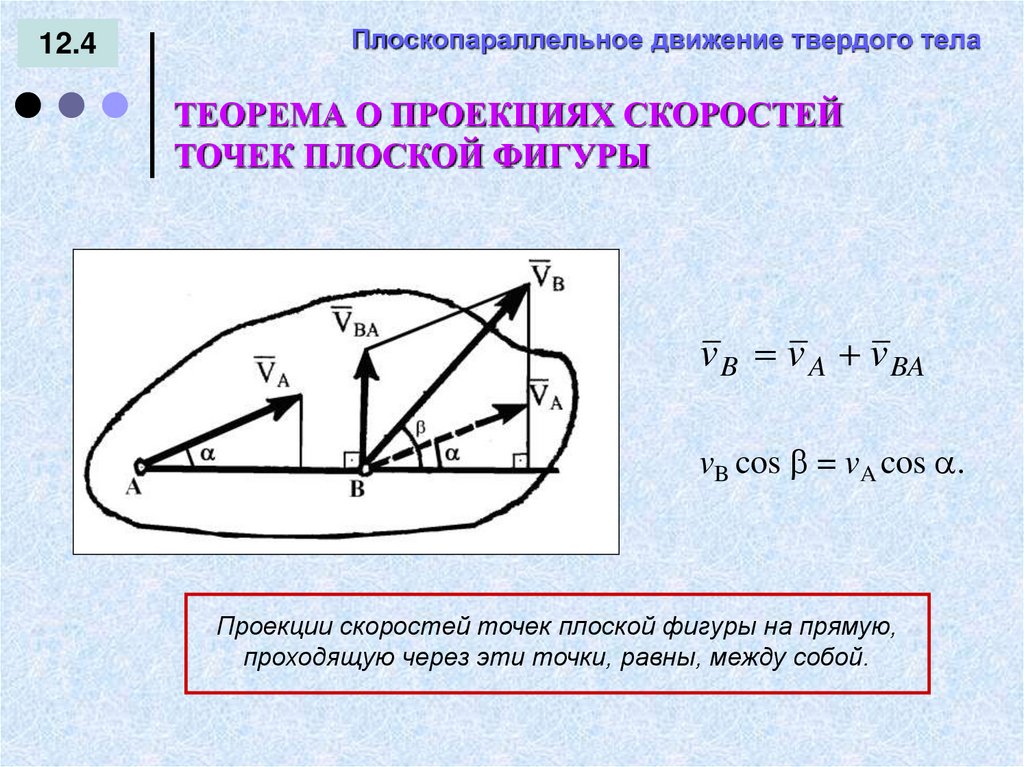
ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ
ТОЧЕК ПЛОСКОЙ ФИГУРЫ
v B v A v BA
vB cos = vA cos .
Проекции скоростей точек плоской фигуры на прямую,
проходящую через эти точки, равны, между собой.

69.

12.5
Плоскопараллельное движение твердого тела
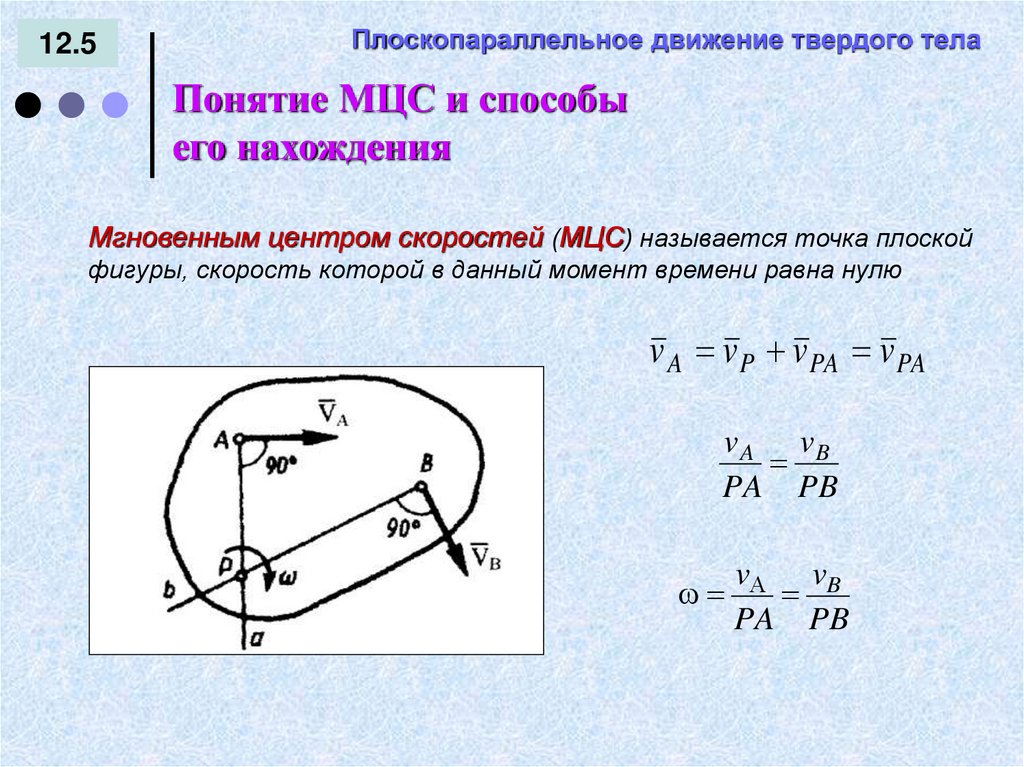
Понятие МЦС и способы
его нахождения
Мгновенным центром скоростей (МЦС) называется точка плоской
фигуры, скорость которой в данный момент времени равна нулю
v A v P v PA v PA
v A vB
PA PB
vА vB
PA PB

70.

12.5
Плоскопараллельное движение твердого тела
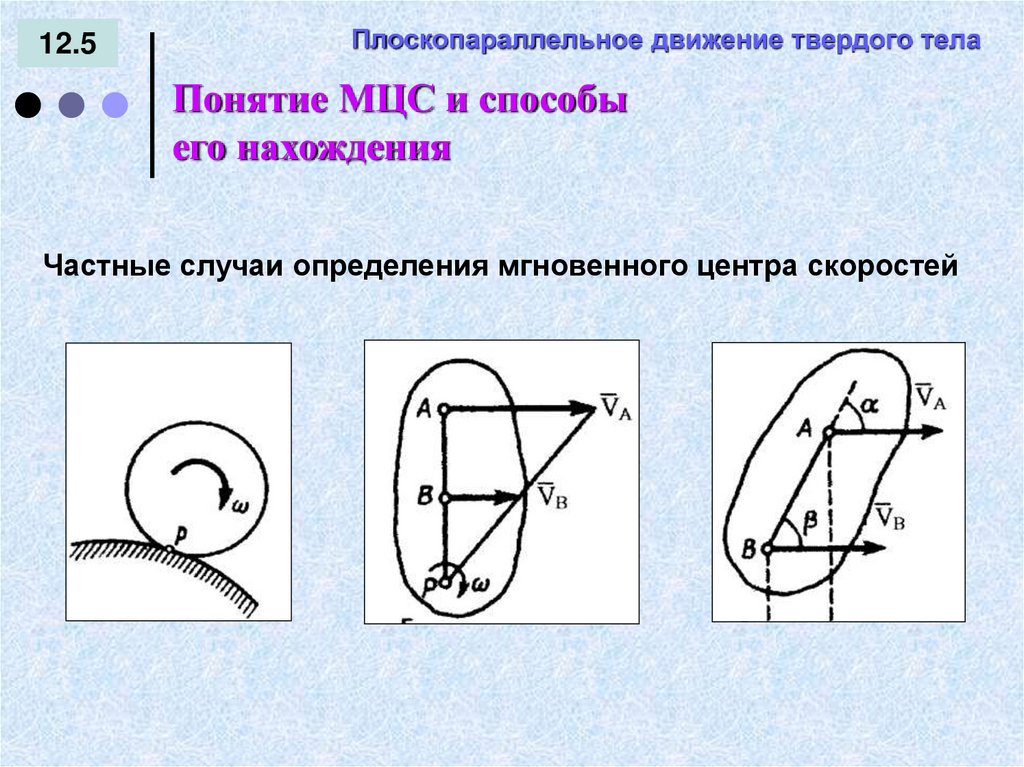
Понятие МЦС и способы
его нахождения
Частные случаи определения мгновенного центра скоростей

71. ЛЕКЦИЯ 13 План:

МЕХАНИКА
13.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
КИНЕМАТИКА
Плоскопараллельное движение
твердого тела
ЛЕКЦИЯ 13
План:
13.1. Определение ускорений точек плоской фигуры
13.2. Мгновенный центр ускорений

72.

13.2
Плоскопараллельное движение твердого тела
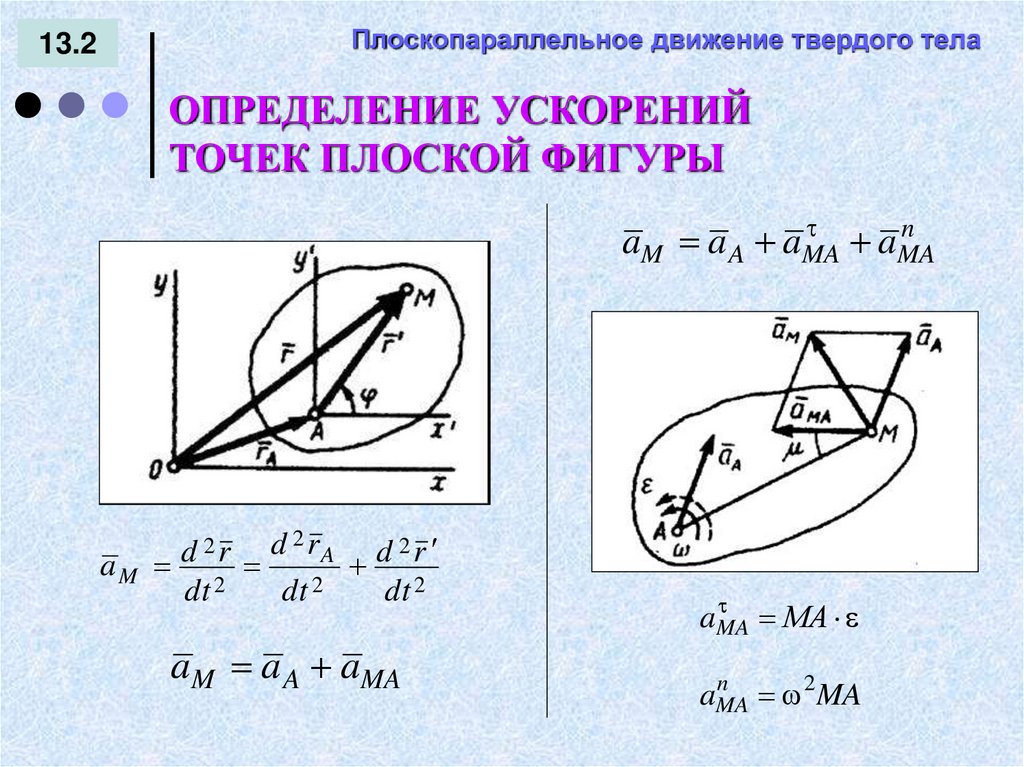
ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ
ТОЧЕК ПЛОСКОЙ ФИГУРЫ
a a a
M
MA
n
aM a A aMA
aMA
2r
d 2 rA d 2 r
d
aM
2
2
dt
dt
dt 2
aM a A aMA
n
aM a A aMA
aMA
A
aMA
МА
n
aMA
2 MA

73.

13.3
Плоскопараллельное движение твердого тела
МГНОВЕННЫЙ ЦЕНТР
УСКОРЕНИЙ
Точка, ускорение которой в данный момент времени равно
нулю называется мгновенным центром ускорений (МЦУ).
aM aQ aMQ aMQ
a M MQ 2 4
tgμ = ε/ω;

74.

Плоскопараллельное движение твердого тела
13.3
МГНОВЕННЫЙ ЦЕНТР
УСКОРЕНИЙ
a M MQ 2 4
tg μ = ε/ω;
Частные случаи :
- если =0, ω≠ 0, то угол = 0 и ускорения всех точек будут
направлены к МЦУ;
- если ≠0, ω = 0, то угол = 90о и ускорения всех точек
направлены перпендикулярно к отрезкам, соединяющим эти точки
с МЦУ

75.

МЕХАНИКА
Теоретическая механика
Модуль 1
Раздел 3 – ДИНАМИКА ТОЧКИ
ОБЩИЕ СВЕДЕНИЯ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
ЛЕКЦИЯ 14
ЛЕКЦИЯ 15
ЛЕКЦИЯ 16

76. ЛЕКЦИЯ 14 План:

МЕХАНИКА
14.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
ДИНАМИКА ТОЧКИ
Общие сведения
ЛЕКЦИЯ 14
План:
14.1. Основные законы механики
14.2. Дифференциальные уравнения движения
материальной точки

77. ДИНАМИКА ТОЧКИ

14.2
ДИНАМИКА ТОЧКИ
ОБЩИЕ СВЕДЕНИЯ
Динамика - это раздел механики, в котором изучается
движение материальных точек, тел и механических систем
под действием приложенных сил
Основные законы механики
Первый закон (закон инерции)
Второй закон (основной закон динамики)
ma F
Третий закон (закон равенства действия и противодействия)
Четвертый закон (закон независимости действия сил)
а а1 а2 ... аn

78. ДИНАМИКА ТОЧКИ

14.3
ДИНАМИКА ТОЧКИ
ОБЩИЕ СВЕДЕНИЯ
Инерция – это свойство
материальной точки оказывать
сопротивление изменению скорости.
ma F и
Сила инерции материальной точки направлена противоположно
ускорению точки и приложена к телу, сообщающему точке это
ускорение

79. ДИНАМИКА ТОЧКИ

14.4
ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Дифференциальные уравнения движения точки
в проекциях на декартовые оси:
2x
d
m
Fkx
2
dt
d2y
m
Fky
2
dt
2
m d z Fkz
dt 2
Закон движения точки:
x = f1(t);
y = f2 (t);
z = f3(t).

80. ДИНАМИКА ТОЧКИ

14.5
ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
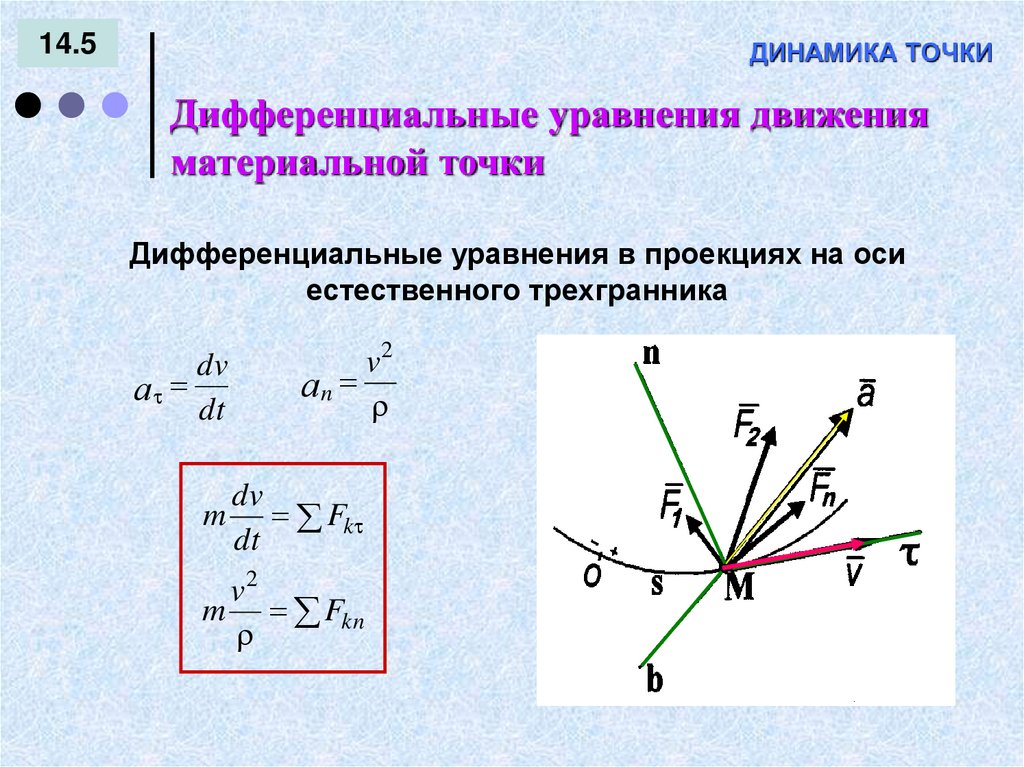
Дифференциальные уравнения в проекциях на оси
естественного трехгранника
dv
а
dt
v2
аn
dv
m Fk
dt
v2
m Fkn

81. ЛЕКЦИЯ 15 План:

МЕХАНИКА
15.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
ДИНАМИКА ТОЧКИ
Дифференциальные уравнения
движения материальной точки
ЛЕКЦИЯ 15
План:
15.1. Две задачи динамики.
15.2. Решение задач

82. ДИНАМИКА ТОЧКИ

15.2
ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
d 2r
m 2 Fk
dt
ДВЕ ЗАДАЧИ ДИНАМИКИ
Первая задача динамики: по известному закону
движения материальной точки находят приложенные к
ней силы.
.
Вторая (основная) задача динамики: при известных
действующих на материальную точку силах, определяют
закон движения точки

83. ДИНАМИКА ТОЧКИ

15.3
ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Решение задач динамики точки:
Первая задача
динамики:
составить и решать дифференциальные
уравнения движения материальной точки
выбрать систему координат и записать
начальные условия;
изобразить движущуюся точку в произвольном
положении и все действующие на точку силы;
составить дифференциальные уравнения
движения точки;
проинтегрировать полученные уравнения,
определив постоянные интегрирования из начальных
условий.
найти искомые величины из полученных
выражений.
Вторая задача
динамики:

84. ДИНАМИКА ТОЧКИ

15.4
ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Лифт весом Р
начинает подъем
по закону:
y = at2.
Решение. На лифт действуют сила
тяжести P и реакция троса T
d2y
m
Fky
2
dt
m y Py T y
(P/g) 2a = T - P,
T = P (1 + 2a/g).
Если лифт опускается с таким же ускорением:
Определить:
натяжение троса Т
Т = Р (1 - 2а/g).

85. ДИНАМИКА ТОЧКИ

15.5
ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Задача 2.
Материальная точка
с массой m движется
под действием
постоянной силы Q
Решение:
Учитывая, что Qx = Q :
dvx
m
Q
dt
vx = (Q/m) t+C1.
dx
= (Q/m) t+C1.
dt
x = (Q/2m)t2+C1t+C2
Найти:
закон движения точки
при начальных условиях:
t=0, x=x0, vx=v0 .
v0 = C1, x0 = C2
x = x0 + v0 t + (Q/2m)t2.

86. ЛЕКЦИЯ 16 План:

МЕХАНИКА
16.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
ДИНАМИКА ТОЧКИ
Дифференциальные уравнения
движения материальной точки
ЛЕКЦИЯ 16
План:
16.1. Свободные прямолинейные колебания материальной точки
16.2. Влияние постоянной силы на свободные колебания точки

87. ДИНАМИКА ТОЧКИ

16.2
ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Свободные прямолинейные колебания
материальной точки
Восстанавливающая сила F - сила,
стремящаяся вернуть точку в положение
равновесия (всегда направлена к положению
равновесия и зависит от величины отклонения
точки от положения равновесия х).
Сила сопротивления R, зависящая от
скорости движения
Возмущающая сила, т.е. сила, являющаяся
заданной функцией времени.
Fх cx
Rх x

88. ДИНАМИКА ТОЧКИ

16.3
ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Свободные прямолинейные колебания материальной
точки
Восстанавливающая
сила
если
c/m = k2, то
x k 2 x 0
Fх cx
m x Fx ,
или
m x сx
дифференциальное уравнение
свободных колебаний
при отсутствии сопротивления.

89. ДИНАМИКА ТОЧКИ

x
16.4
ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Свободные прямолинейные колебания материальной
точки
x k 2 x 0
Характеристическое
уравнение:
Пусть
C1 = Acos ,
C2 = Asin ,
х = А (sin kt cos + cos kt sin )
x = ent
или
n2 + k2 = 0, n1,2 = ± ik
закон гармонических колебаний точки:
общее решение
x = C1 sin kt + C2 cos kt,
x = Asin (kt + ).
Скорость точки: vx =
Ak cos (kt + ).

90. ДИНАМИКА ТОЧКИ

16.5
ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Свободные прямолинейные колебания материальной
точки
x = A sin (kt + )
A - амплитуда колебаний.
(kt+ )= - фаза колебаний.
- начальная фаза колебаний.
k - круговая частота колебаний
Период колебаний Т промежуток времени, в течение
которого точка совершает одно
полное колебание
T = 2 /k.
Частота колебаний ν – число
колебаний, совершаемых за 1с
= 1/T = k/2 .

91. ДИНАМИКА ТОЧКИ

16.6
ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Влияние постоянной силы на свободные колебания
точки
точка равновесия
(P F )
Fx = - с(х + ст)
В результате
const
m x cx
или
статическое отклонение
P= const
F = cx
В точке равновесия при x= ст
F=P = с ст
x k 2 x 0
Т 2 m cт / P

92.

МЕХАНИКА
Теоретическая механика
Модуль 1
Раздел 4 – ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
ЛЕКЦИЯ 17
ЛЕКЦИЯ 18
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
ЛЕКЦИЯ 19
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
ЛЕКЦИЯ 20
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ
ЭНЕРГИИ
ЛЕКЦИЯ 21

93. ЛЕКЦИЯ 17 План:

МЕХАНИКА
17.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
ЛЕКЦИЯ 17
План:
17.1. Введение в динамику системы. Свойства внутренних сил.
17.2. Центр масс механической системы
17.3. Теорема о движении центра масс механической системы
17.4. Закон сохранения движения центра масс.
17.5. Примеры применения теоремы о движении центра масс.

94. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

17.2
ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
Введение в динамику системы
Механическая система - совокупность материальных точек или
тел, находящихся в механическом взаимодействии
Fke - Внешние силы, действующие на точки системы со стороны
точек или тел, не входящих в состав данной системы
Fki - Внутренние силы, с которыми точки или тела данной системы
действуют друг на друга
Свойства внутренних сил:
Fki 0
i
m
(
F
0 k ) 0

95. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

17.3
ОБЩИЕ
ТЕОРЕМЫ
ДИНАМИКИ
ТЕОРЕМА О ДВИЖЕНИИ
ЦЕНТРА
МАСС
Центр масс механической системы
Масса системы: M mk
Центром масс (центром инерции) механической системы называется
геометрическая точка С, координаты которой :
mk xk
x
С
M
mk yk
у
С
M
Радиус-вектор центра масс:
mk zk
zC
M
mk rk
r
C
M

96. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

17.4
ТЕОРЕМА
О ДВИЖЕНИИ ЦЕНТРА МАСС
Для каждой точки системы
mk ak Fke Fki
mk a k Fke Fki
d 2 rk
d 2 rC
mk 2 M 2
dt
dt
mk rk
rC
M
mk rk MrC
mk a k MaC
a C — ускорение центра
масс системы
Мa C Fke
d 2 хC
e
M
F
kx
2
dt
d 2 уC
e
M
F
kу
2
dt
d 2 zC
e
M
F
kz
dt 2
Дифференциальные уравнения
движения центра масс в проекциях
на оси координат

97. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

17.5
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
Мa C Fke
Закон сохранения движения
центра масс
1. Пусть сумма внешних сил, действующих на систему, равна нулю
e
F
k 0
aC 0
vC сonst
2. Пусть сумма внешних сил системы, не равна нулю, но сумма их
проекций на какую-нибудь ось равна нулю
Fke 0
Fkхe 0
М x C 0
x C 0
x C vCx const

98. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

17.6
ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
Примеры применения теоремы о
движении центра масс
Действие пары сил на тело
Fke F F ' 0
aC 0
vC сonst v0C 0
Движение по горизонтальной плоскости
Fтр
F
F’

99. ЛЕКЦИЯ 18 План:

МЕХАНИКА
18.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
ЛЕКЦИЯ 18
План:
18.1. Количество движения.
18.2. Импульс силы.
18.3. Теорема об изменении количества движения
18.4. Закон сохранения количества движения.

100. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

18.2
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
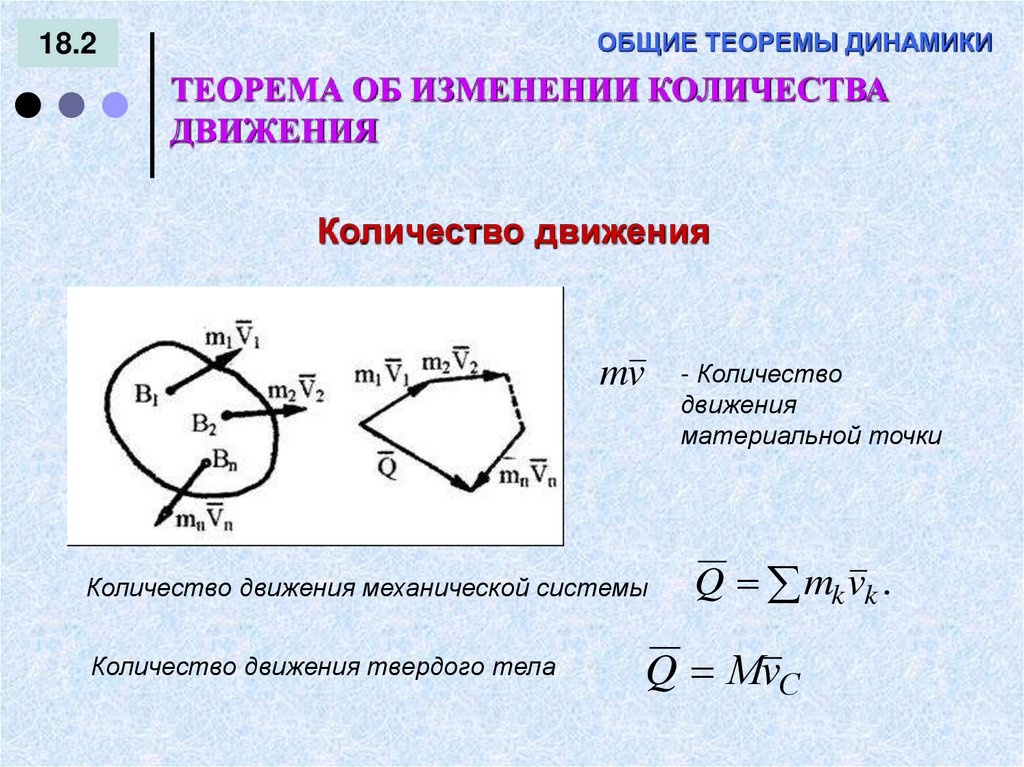
Количество движения
mv
- Количество
движения
материальной точки
Количество движения механической системы
Количество движения твердого тела
Q mk vk .
Q МvС

101. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

18.3
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
Импульс силы
Элементарный импульс силы:
dS Fdt
Импульс силы за конечный промежуток времени t1:
t1
S F dt.
0
Проекции импульса на координатные оси
t1
t1
t1
S у Fу dt .
S x Fx dt.
S z Fz dt.
0
0
0
Единицей измерения импульса силы в системе СИ является 1
кг м/с = 1 Н/с.

102. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

18.4
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
Дифференциальное уравнение движения точки
t1
d ( mv )
Fk .
dt
mv mv0 Fk dt .
0
mv mv0 Sk
Теорема об изменении количества
движения материальной точки
mv1x mv0 x Skx ,
mv1 y mv0 y Sky ,
mv1z mv0 z Skz.

103. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

18.5
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
mk a k Fke Fki
Для всех точек механической системы
d m v dQ .
m
a
k k
k k
dt
dt
=0
Теорема об изменении количества движения системы:
dQ
Fke .
dt
t1
Q1 Q0 Fke dt
0
dQ y
dQx
dQz
e
e
Fkx ,
Fkze .
Fky ,
dt
dt
dt
e
Q1 Q0 S k
e
Q1x Qox S kx
e
Q1 y Qoy S ky
e
Q1z Qoz S kz

104. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

17.10
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
Закон сохранения количества
движения
1.
2.
Fke 0.
Fkхe 0.
dQ
Fke 0
dt
dQx
e
Fkx
0
dt
Q const
Qх const

105. ЛЕКЦИЯ 19 План:

МЕХАНИКА
19.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
ЛЕКЦИЯ 19
План:
19.1. Осевые моменты инерции тела.
19.2. Момент количества движения материальной точки.
19.3. Теорема об изменении момента количества движения точки

106. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

19.2
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
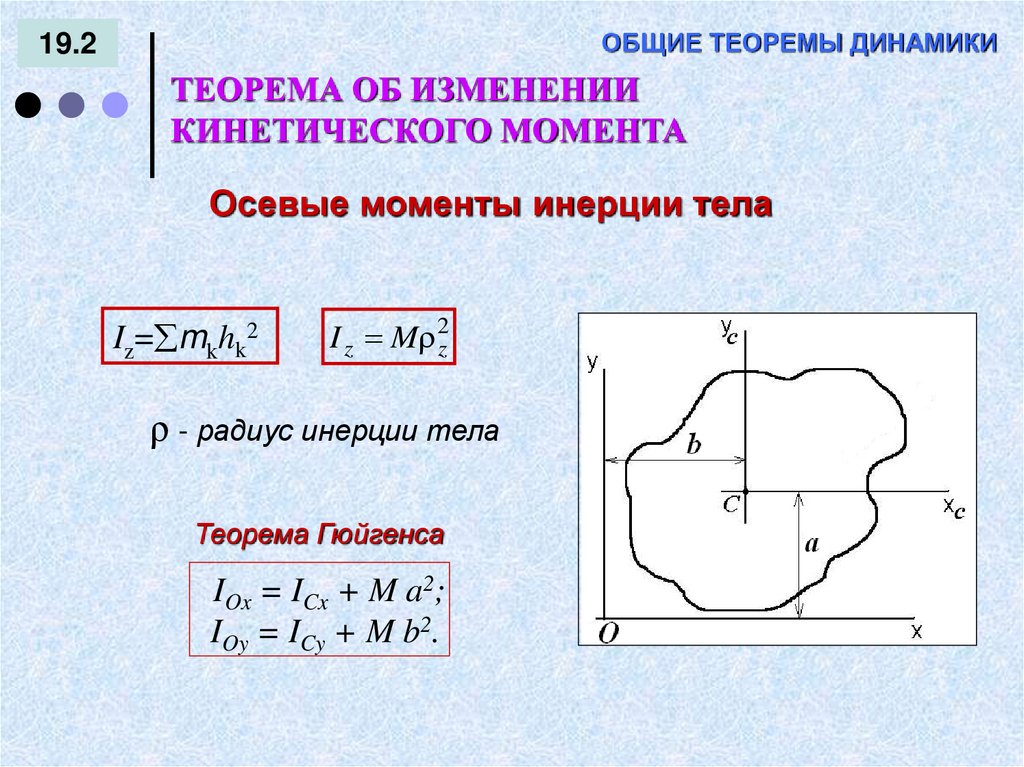
Осевые моменты инерции тела
Iz= mkhk2
I z M 2z
ρ - радиус инерции тела
Теорема Гюйгенса
IOx = ICx + M a2;
IOy = ICy + M b2.

107. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

19.3
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
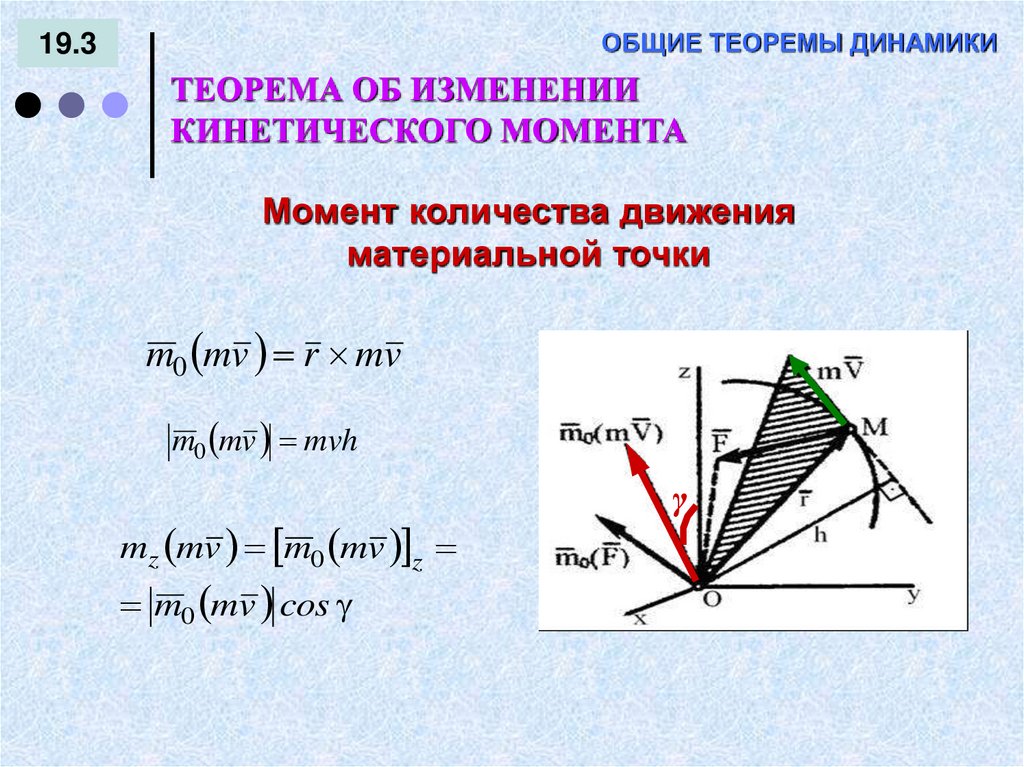
Момент количества движения
материальной точки
m0 mv r mv
m0 mv mvh
mz mv m0 mv z
m0 mv cos
γ

108. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

19.4
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
Теорема об изменении
момента количества движения точки
d r mv dr mv r m dv v mv r ma .
dt
dt
dt
v mv 0
d
r mv r F
dt
d
m0 (mv ) m0 ( F )
dt
или

109. ЛЕКЦИЯ 20 План:

МЕХАНИКА
20.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
ЛЕКЦИЯ 20
План:
20.1. Теорема об изменении кинетического момента.
20.2. Дифференциальное уравнение вращения твёрдого тела

110. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

20.2
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
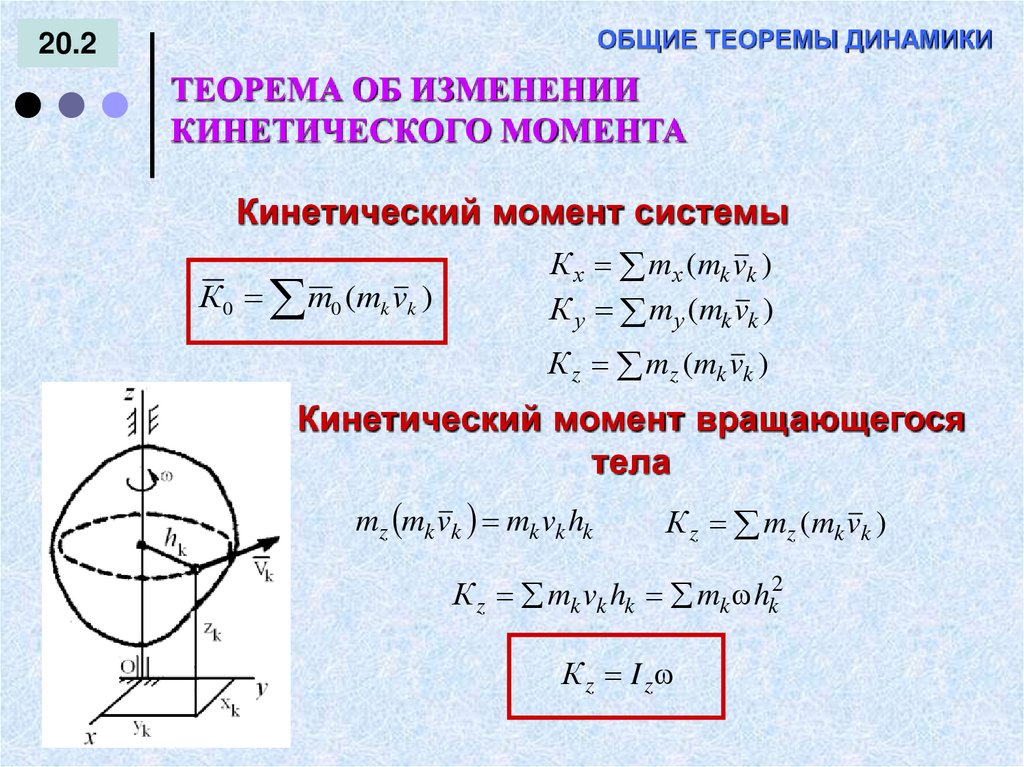
Кинетический момент системы
К 0 m0 (mk vk )
К х mх (mk vk )
К у mу (mk vk )
К z mz (mk vk )
Кинетический момент вращающегося
тела
mz mk vk mk vk hk
К z mz (mk vk )
К z mk vk hk mk hk2
К z I z

111. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

20.3
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
Если рассмотреть одну точку системы:
d [m (m v )] m ( F e ) m ( F i ) ,
0
k k
0 k
0 k
dt
для всех точек системы:
=0
d [ m ( m v )] m ( F e ) m ( F i ) .
0 k k
0 k 0 k
dt
dK 0
m0 ( Fke )
dt
Теорема об изменении кинетического
момента механической системы
dK x
mx ( Fke )
dt
dK y
my ( Fke )
dt
dK z
mz ( Fke )
dt

112. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

20.4
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
следствия из теоремы:
dK 0
m0 ( Fke )
dt
dK z
mz ( Fke )
dt
1. Если сумма моментов всех внешних сил, действующих на
систему, относительно центра О равна нулю
m0 ( Fke ) 0
то
K0 const
2. Если сумма моментов всех внешних сил, действующих на
систему, относительно некоторой неподвижной оси равна нулю
mz ( Fke ) 0
то
Kz = const

113. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

20.5
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
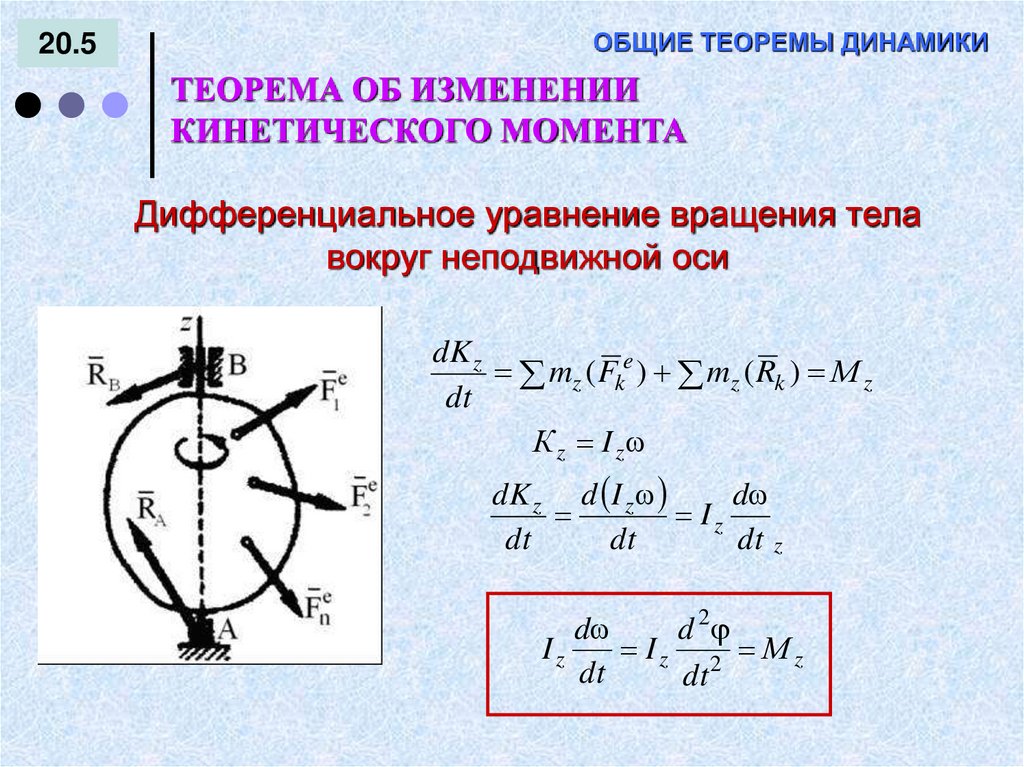
Дифференциальное уравнение вращения тела
вокруг неподвижной оси
dK z
mz ( Fke ) mz ( Rk ) М z
dt
К z I z
dK z d I z
d
Iz
dt
dt
dt z
d
d 2
Iz
Iz 2 М z
dt
dt

114. ЛЕКЦИЯ 21 План:

МЕХАНИКА
21.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
ЛЕКЦИЯ 21
План:
21.1. Работа силы и мощность

115. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

21.3
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ
ЭНЕРГИИ
Работа силы. Мощность
Элементарная работа силы
dA = F ds, где F = F cos ,
dA = Fds cos .
Работа силы на конечном перемещении
1. ( F const)
( M1 )
A( M 0 M1 ) F ds
(M 0 )
2. ( F const)
A( M 0 M1 ) F s1 Fs1cos

116. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

21.4
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Работа силы. Мощность
Если вектор силы спроецировать на оси координат
( M1 )
A( M 0 M1 ) ( Fx dx Fy dy Fz dz)
(M 0 )
Единицей измерения работы в системе СИ является - 1 джоуль
(1 Дж = 1H м = 1 кг м2 /с2).
Мощность - это величина, определяющая работу, совершаемую
силой в единицу времени.
N = dA/dt = F ds/dt = F v.
Единицей измерения мощности в системе СИ является ватт
(1 Вт = 1Дж/с). В технике - 1 л.с. = 736 Вт.

117. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

21.5
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Примеры вычисления работы
Работа силы тяжести
z1
A( M 0 M1 ) ( P)dz P( z0 z1 )
z0
z0 - z1 = h
A( M 0 M1 ) Р h
Работа силы тяжести не зависит от формы траектории точки её
приложения. Силы, обладающие таким свойством, называются
потенциальными силами.

118. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

21.6
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Работа силы. Мощность
Работа силы упругости
F = cλ = c x и Fx = -cx.
x1
c
A( M 0 M1 ) ( cx)dx ( x02 x12 ).
2
x0
A( M 0 M 1 )
с 2
( 0 21 ) ,
2

119. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

21.7
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Работа силы. Мощность
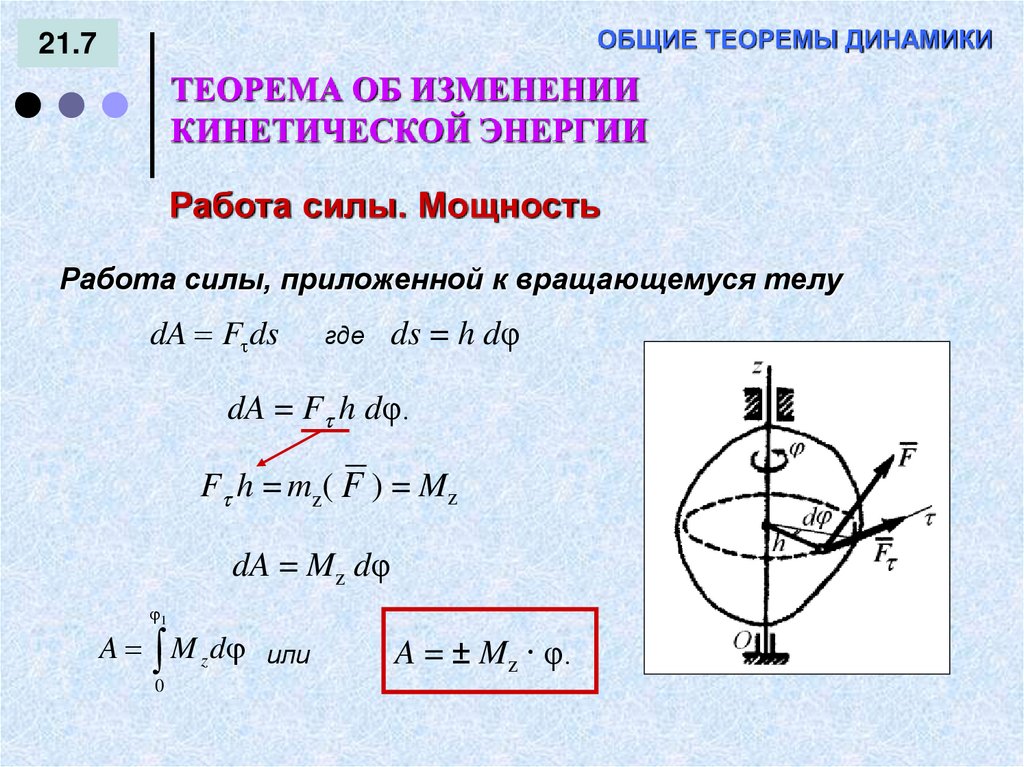
Работа силы, приложенной к вращающемуся телу
dA F ds
где
ds = h dφ
dA = F h dφ.
F h = mz( F ) = Mz
dA = Mz dφ
1
A M z d или
0
A = ± Mz ∙ φ.

120. ЛЕКЦИЯ 22 План:

МЕХАНИКА
22.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
ЛЕКЦИЯ 22
План:
22.1. Кинетическая энергия.
22.2. Теорема об изменении кинетической энергии

121. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

22.2
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ
ЭНЕРГИИ
Кинетическая энергия
для материальной точки
для механической системы
из n материальных точек
M
V
v2
m
2
vk2
T mk
2
k 1
n
Кинетическая энергия - скалярная величина
Единица измерения кинетической энергии в системе СИ - 1 Дж.

122. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

22.3
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Кинетическая энергия
для твердого тела
Поступательное движение
Вращательное движение
2
T Iz
2
vС2
М
2
Плоскопараллельное движение
2
Tпл I P
2
v2
2
Tпл M
Iс
2
2

123. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

22.4
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Рассмотрим материальную точку с массой m
ma = Fk .
M
a
dv dv ds
dv
v
dt ds dt
ds
V
mv
mv 2
d(
) dAk
2
теорема об изменении
кинетической энергии точки
в дифференциальной форме
dv
Fk
ds
mvdv dAk
mv12 mv02
А(М0М1 )
2
2
теорема об изменении
кинетической энергии точки
в конечном виде

124. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

22.5
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Рассмотрим материальную точку механической системы с массой mk
d(
mk v 2k
2
) dAek dAik
Для всей механической системы
d (
mk v 2k
2
) dAek dAik
dT dAek dAik
T Т 0 Aek Aik
теорема об изменении
кинетической энергии системы
в дифференциальной форме
теорема об изменении
кинетической энергии системы
в интегральной форме

125.

МЕХАНИКА
Теоретическая механика
Модуль 1
Раздел 5 – АНАЛИТИЧЕСКАЯ МЕХАНИКА
ПРИНЦИП ДАЛАМБЕРА
ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
ЛЕКЦИЯ 23
ЛЕКЦИЯ 24
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
ЛЕКЦИЯ 25
УРАВНЕНИЯ ЛАГРАНЖА
ЛЕКЦИЯ 18
ЛЕКЦИЯ 26

126. ЛЕКЦИЯ 23 План:

МЕХАНИКА
23.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
АНАЛИТИЧЕСКАЯ МЕХАНИКА
ПРИНЦИП ДАЛАМБЕРА
ЛЕКЦИЯ 23
План:
23.1. Сила инерции.
23.2. Принцип Даламбера для материальной точки и
механической системы.
23.3. Главный вектор и главный момент сил инерции
23.4. Динамические реакции.

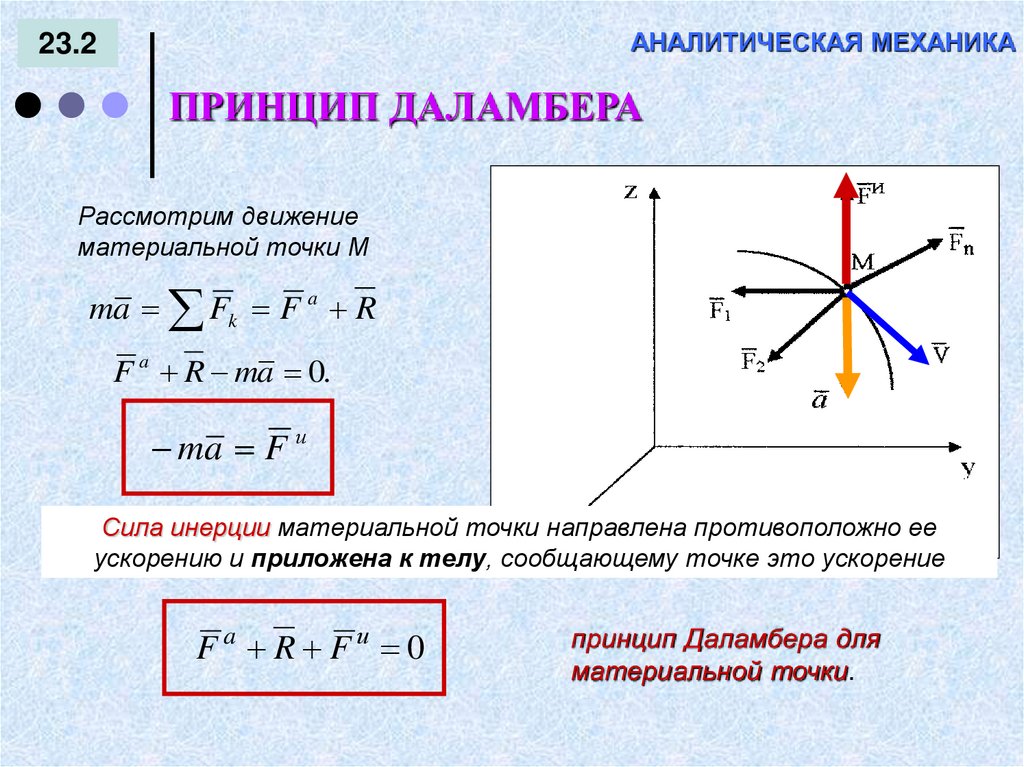
127. АНАЛИТИЧЕСКАЯ МЕХАНИКА

23.2
ПРИНЦИП ДАЛАМБЕРА
Рассмотрим движение
материальной точки М
ma Fk F a R
F a R ma 0.
ma F и
Сила инерции материальной точки направлена противоположно ее
ускорению и приложена к телу, сообщающему точке это ускорение
Fa R Fи 0
принцип Даламбера для
материальной точки.

128. АНАЛИТИЧЕСКАЯ МЕХАНИКА

23.3
ПРИНЦИП ДАЛАМБЕРА
Рассмотрим материальную точку механической системы:
Fka Rk Fku 0
для всех точек полученная система сил будет произвольной
пространственной и уравновешенной:
F F F 0
m F m F m F 0
Принцип Даламбера
для системы
и
m0 Fk M 0 0
Принцип Даламбера
для твердого тела
e
k
0
i
k
e
k
и
k
0
i
k
0
и
k
Fk R и 0

129. АНАЛИТИЧЕСКАЯ МЕХАНИКА

23.4
ПРИНЦИП ДАЛАМБЕРА
Главный вектор и главный момент
сил инерции механической системы
Главный вектор сил инерции
R u maC
и
R maC
Главный момент сил инерции
M 0и
R и Fku
dK 0
dt
R nu maCn
M 0и m0 Fkи
dK z
и
Mz
dt

130. АНАЛИТИЧЕСКАЯ МЕХАНИКА

23.5
ПРИНЦИП ДАЛАМБЕРА
Частные случаи приведения сил инерции твердого тела
1. Поступательное движение
R и maC
2. Вращательное движение (общий случай)
R и maC
M 0иz J 0 z
d
J 0z
dz
3. Вращение вокруг оси, проходящей через центр масс тела
и
M Сz
J Сz
4. Плоскопараллельное движение
и
R maC
и
M Сz
J Сz

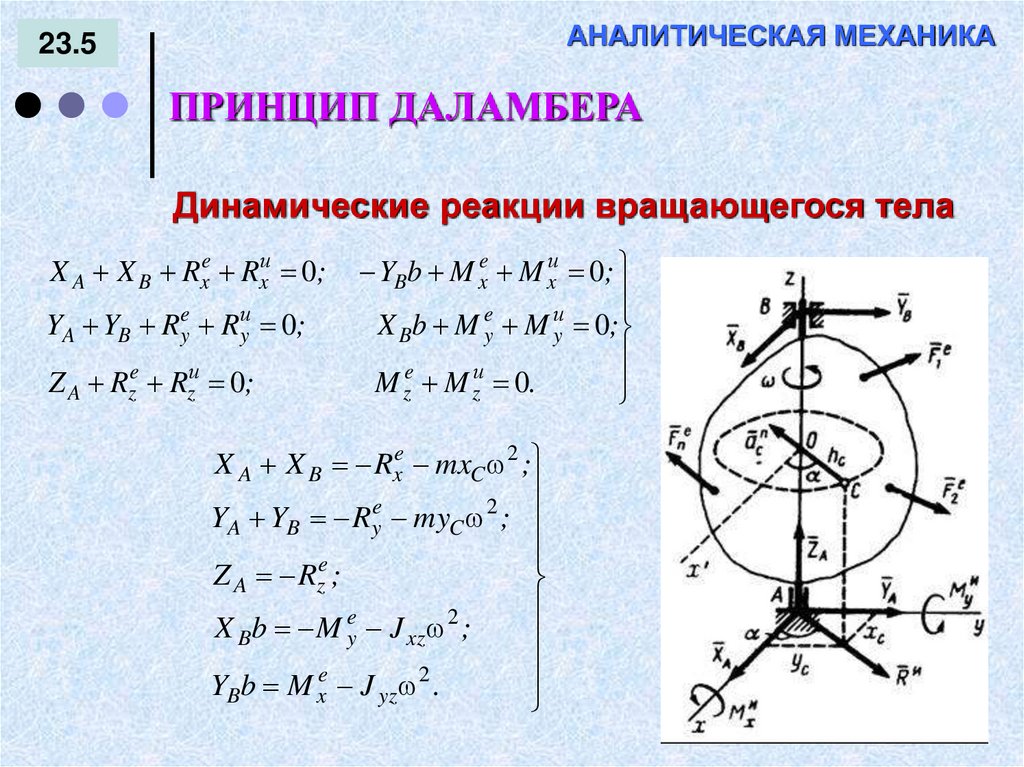
131. АНАЛИТИЧЕСКАЯ МЕХАНИКА

23.5
ПРИНЦИП ДАЛАМБЕРА
Динамические реакции вращающегося тела
X A X B Rxe Rxи 0;
YA YB Rye Rиy 0;
Z A Rze Rzи 0;
YBb M xe M xи 0;
e
и
X Bb M y M y 0;
e
и
M z M z 0.
X A X B Rxe mxC 2 ;
e
2
YA YB R y myC ;
e
Z A Rz ;
X Bb M ye J xz 2 ;
e
2
YBb M x J yz .

132. ЛЕКЦИЯ 24 План:

МЕХАНИКА
24.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
АНАЛИТИЧЕСКАЯ МЕХАНИКА
ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
ЛЕКЦИЯ 24
План:
24.1. Классификация связей.
24.2. Возможные перемещения системы. Идеальные связи.
24.3. Принцип возможных перемещений

133. АНАЛИТИЧЕСКАЯ МЕХАНИКА

24.2
ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
Классификация связей
Связи - это любого вида ограничения, которые налагаются на
положения и скорости точек механической системы
Стационарные
Нестационарные
Геометрические
Кинематические
(дифференциальные)
Интегрируемые
Неинтегрируемые
Голономные
Неголономные
Удерживающие
Неудерживающие

134. АНАЛИТИЧЕСКАЯ МЕХАНИКА

24.3
ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
Возможные перемещения системы
Возможное перемещение механической системы - это совокупность
воображаемых элементарных перемещений точек системы из
занимаемого в данный момент положения, которые допускаются всеми
наложенными на систему связями
действительное перемещение - dr
дифференциал r r (t )
возможное перемещение – r
вариация r r (t )
х, у, z - проекции r
на координатные оси
s r

135. АНАЛИТИЧЕСКАЯ МЕХАНИКА

24.4
ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
Число степеней свободы системы - это
число независимых, между собой возможных
перемещений механической системы
Возможная работа - элементарная работа,
которую действующая на материальную точку
сила могла бы совершить на перемещении,
совпадающем с возможным перемещением этой
точки:
А F r
Идеальная связь – это связь, для которой сумма элементарных
работ ее реакций на любом возможном перемещении системы
равна нулю:
Аk Rk rk 0
R

136. АНАЛИТИЧЕСКАЯ МЕХАНИКА

24.5
ПРИНЦИП ВОЗМОЖНЫХ
ПЕРЕМЕЩЕНИЙ
(общее условие равновесия механической системы)
Для равновесия механической системы с идеальными связями
необходимо и достаточно, чтобы сумма элементарных работ
всех активных сил на любом возможном перемещении
системы была равна нулю:
Aka 0
a
a
F
r
F
k
k sk cos k 0
k

137. ЛЕКЦИЯ 25 План:

МЕХАНИКА
25.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
АНАЛИТИЧЕСКАЯ МЕХАНИКА
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
ЛЕКЦИЯ 25
План:
25.1.Обобщённые координаты и обобщенные скорости.
25.2. Обобщённые силы.
25.3. Общее уравнение динамики

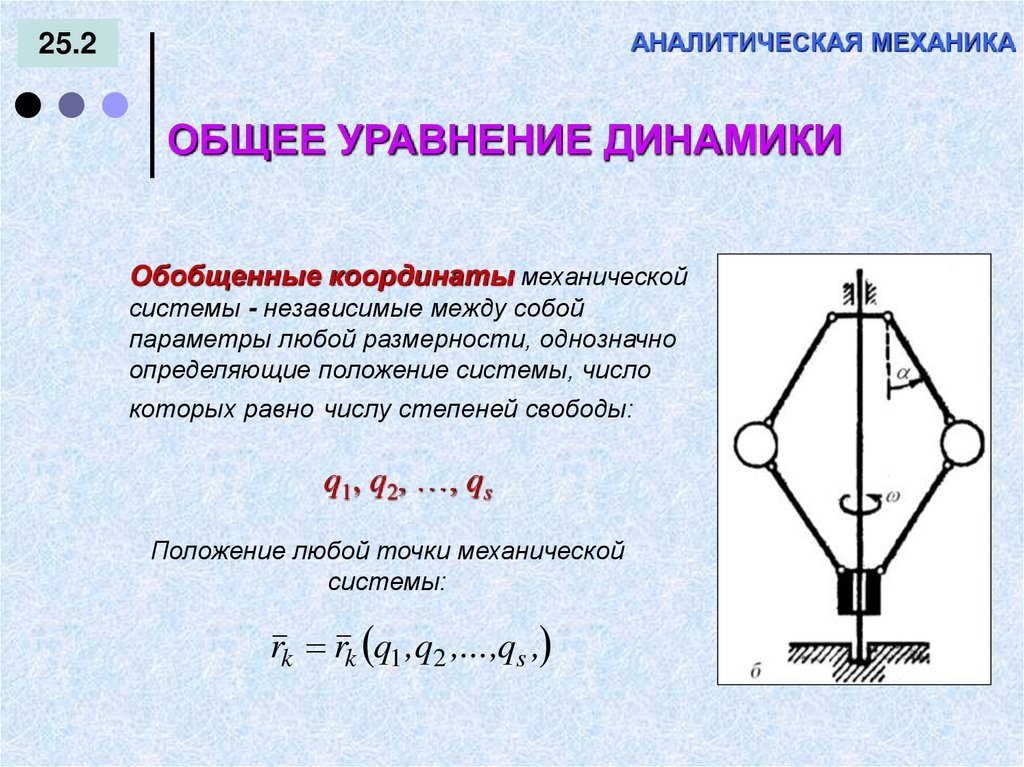
138. АНАЛИТИЧЕСКАЯ МЕХАНИКА

25.2
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
Обобщенные координаты механической
системы - независимые между собой
параметры любой размерности, однозначно
определяющие положение системы, число
которых равно числу степеней свободы:
q1, q2, …, qs
Положение любой точки механической
системы:
rk rk q1 ,q2 ,...,qs ,

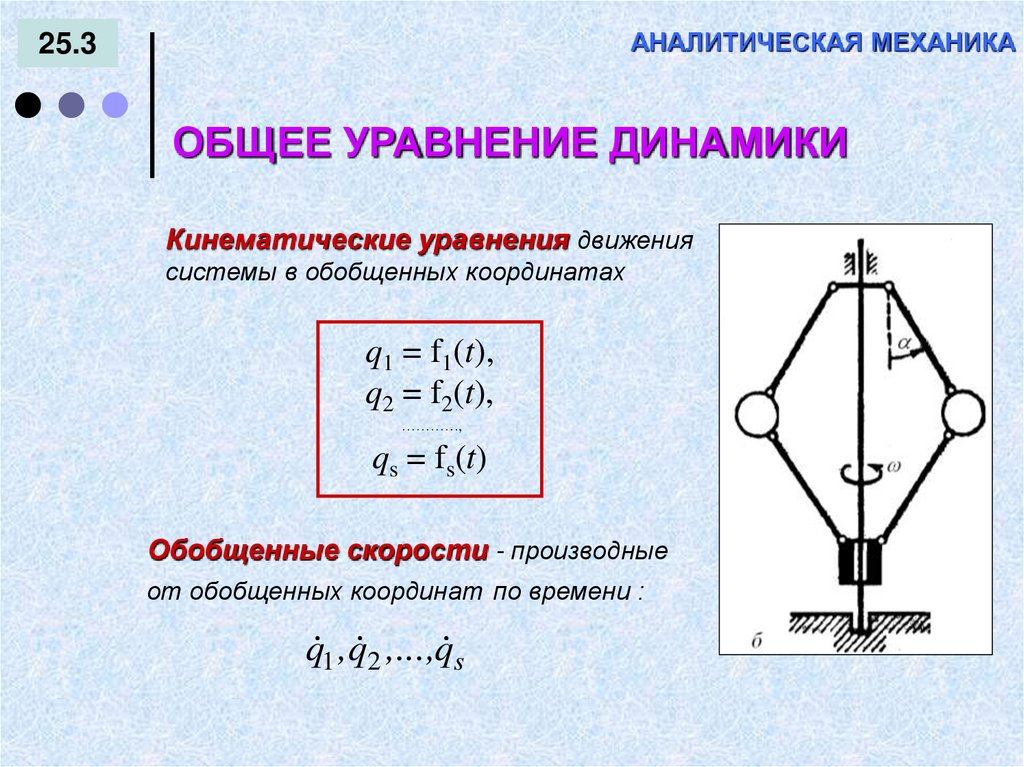
139. АНАЛИТИЧЕСКАЯ МЕХАНИКА

25.3
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
Кинематические уравнения движения
системы в обобщенных координатах
q1 = f1(t),
q2 = f2(t),
…………,
qs = fs(t)
Обобщенные скорости - производные
от обобщенных координат по времени :
q 1 ,q 2 ,...,q s

140. АНАЛИТИЧЕСКАЯ МЕХАНИКА

25.4
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
Обобщённые силы
Пусть механическая система состоит из n материальных
точек, на которые действуют силы : F1 , F2 ,...,Fn
Сумма элементарных работ всех сил на возможном
перемещении системы δq:
Ak F1 r1 F2 r2 Fn rn
rk q
A1
Q1
q1
A1 = Q1 q1
- обобщенная сила, соответствующая
обобщенной координате q

141. АНАЛИТИЧЕСКАЯ МЕХАНИКА

25.5
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
Если ко всем точкам системы кроме активных сил и реакций
связей прибавить силы инерции, то по принципу Даламбера
полученная система сил будет уравновешенной
Тогда, согласно принципу возможных перемещений:
Aka Akи AkR 0
= 0 для идеальных связей
Aka Akи 0
общее уравнение динамики
(принцип Даламбера–Лагранжа)

142. АНАЛИТИЧЕСКАЯ МЕХАНИКА

25.6
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
Общее уравнение динамики в обобщенных координатах:
Q j Qиj q j 0
обобщенная
активная сила
обобщенная сила инерции,
соответствующая
обобщенной координате qj
Q1 Q1и 0
Т.к. величины qj независимы, то:
Q2 Q2и 0
……….,
QS QSи 0

143. ЛЕКЦИЯ 26 План:

МЕХАНИКА
26.1
Модуль 1
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
АНАЛИТИЧЕСКАЯ МЕХАНИКА
УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
ЛЕКЦИЯ 26
План:
26.1. Уравнения Лагранжа

144. АНАЛИТИЧЕСКАЯ МЕХАНИКА

26.2
АНАЛИТИЧЕСКАЯ МЕХАНИКА
УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
Лагранж получил формулу, вычисляющую обобщенные силы
и
Q
инерции
j через кинетическую энергию системы:
d T T
Qиj
dt q j q
:
где Т - кинетическая энергия системы
Согласно общему уравнению динамики:
обобщенная сила системы:
Q j Qиj 0
d T T
и
Q j Q j
dt q j q

145. АНАЛИТИЧЕСКАЯ МЕХАНИКА

26.3
УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
Дифференциальные уравнения движения системы в
обобщенных координатах (уравнения Лагранжа)
:
d T T
Q2 ,
dt q 2 q2
. . . . . . . . .
d T T
Qs .
dt q s qs
d T T
Q1 ,
dt q 1 q1

146. АНАЛИТИЧЕСКАЯ МЕХАНИКА

26.4
АНАЛИТИЧЕСКАЯ МЕХАНИКА
УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
Чтобы составить уравнения Лагранжа для данной
механической системы, необходимо:
- установить число степеней свободы системы и выбрать
обобщенные координаты;
- изобразить систему в произвольном положении,все
:
действующие силы (для систем с идеальными связями только
активные);
- вычислить обобщенные силы, при этом каждое возможное
перемещение должно быть положительным;
- записать кинетическую энергию системы и выразить ее через
обобщенные координаты и обобщенные скорости;
- вычислить частные производные согласно уравнениям
Лагранжа;