Similar presentations:
Теоретическая механика. Модуль 1. Раздел 3 – динамика точки
1.
МЕХАНИКАТеоретическая механика
Модуль 1
Раздел 3 –
ДИНАМИКА ТОЧКИ
ОБЩИЕ СВЕДЕНИЯ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
ЛЕКЦИЯ 14
ЛЕКЦИЯ 15
ЛЕКЦИЯ 16
2. ДИНАМИКА ТОЧКИ
14.2ДИНАМИКА ТОЧКИ
ОБЩИЕ СВЕДЕНИЯ
Динамика - это раздел механики, в котором изучается
движение материальных точек, тел и механических систем
под действием приложенных сил
Основные законы механики
Первый закон (закон инерции)
Второй закон (основной закон динамики)
ma F
Третий закон (закон равенства действия и противодействия)
Четвертый закон (закон независимости действия сил)
а а1 а2 ... аn
3. ДИНАМИКА ТОЧКИ
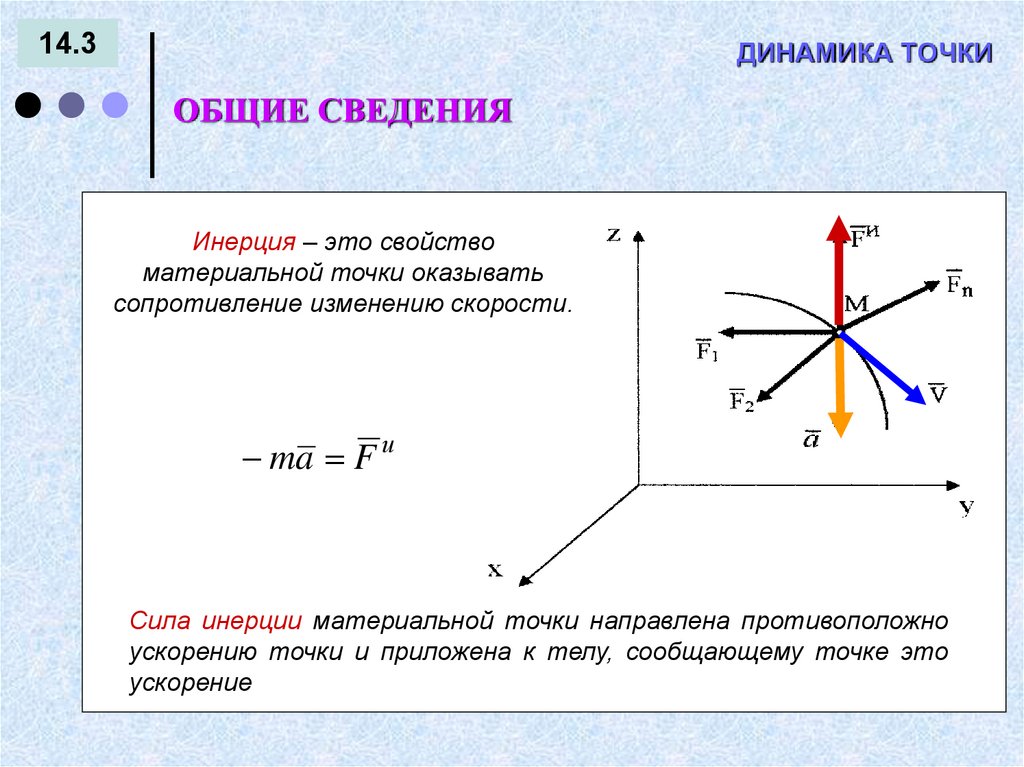
14.3ДИНАМИКА ТОЧКИ
ОБЩИЕ СВЕДЕНИЯ
Инерция – это свойство
материальной точки оказывать
сопротивление изменению скорости.
ma F и
Сила инерции материальной точки направлена противоположно
ускорению точки и приложена к телу, сообщающему точке это
ускорение
4. ДИНАМИКА ТОЧКИ
14.4ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Дифференциальные уравнения движения точки
в проекциях на декартовые оси:
2x
d
m
Fkx
2
dt
d2y
m
Fky
2
dt
2
m d z Fkz
dt 2
Закон движения точки:
x = f1(t);
y = f2 (t);
z = f3(t).
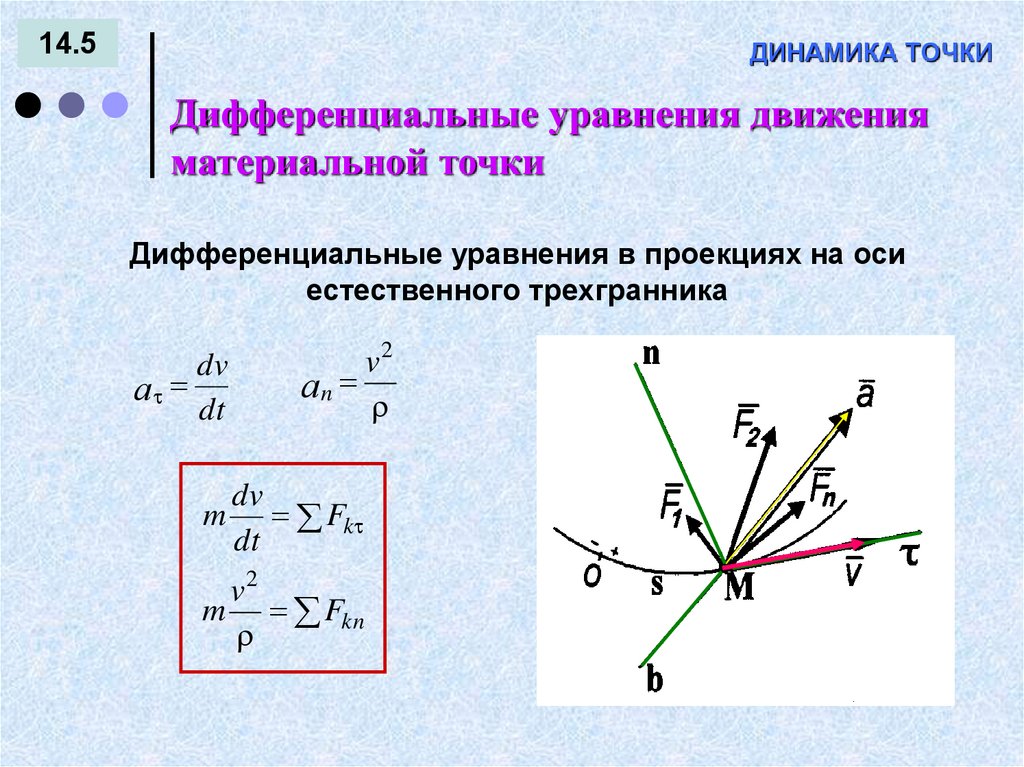
5. ДИНАМИКА ТОЧКИ
14.5ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Дифференциальные уравнения в проекциях на оси
естественного трехгранника
dv
а
dt
v2
аn
dv
m Fk
dt
v2
m Fkn
6. ДИНАМИКА ТОЧКИ
15.2ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
d 2r
m 2 Fk
dt
ДВЕ ЗАДАЧИ ДИНАМИКИ
Первая задача динамики: по известному закону
движения материальной точки находят приложенные к
ней силы.
.
Вторая (основная) задача динамики: при известных
действующих на материальную точку силах, определяют
закон движения точки
7. ДИНАМИКА ТОЧКИ
15.3ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Решение задач динамики точки:
Первая задача
динамики:
составить и решать дифференциальные
уравнения движения материальной точки
выбрать систему координат и записать
начальные условия;
изобразить движущуюся точку в произвольном
положении и все действующие на точку силы;
составить дифференциальные уравнения
движения точки;
проинтегрировать полученные уравнения,
определив постоянные интегрирования из начальных
условий.
найти искомые величины из полученных
выражений.
Вторая задача
динамики:
8. ДИНАМИКА ТОЧКИ
15.4ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Лифт весом Р
начинает подъем
по закону:
y = at2.
Решение. На лифт действуют сила
тяжести P и реакция троса T
d2y
m
Fky
2
dt
m y Py T y
(P/g) 2a = T - P,
T = P (1 + 2a/g).
Если лифт опускается с таким же ускорением:
Определить:
натяжение троса Т
Т = Р (1 - 2а/g).
9. ДИНАМИКА ТОЧКИ
15.5ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Задача 2.
Материальная точка
с массой m движется
под действием
постоянной силы Q
Решение:
Учитывая, что
Qx = Q :
dvx
m
Q
dt
vx = (Q/m) t+C1.
dx
= (Q/m) t+C1.
dt
x = (Q/2m)t2+C1t+C2
Найти:
закон движения точки
при начальных условиях:
t=0, x=x0, vx=v0 .
v0 = C1, x0 = C2
x = x0 + v0 t + (Q/2m)t2.
10. ДИНАМИКА ТОЧКИ
16.2ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Свободные прямолинейные колебания
материальной точки
Восстанавливающая сила F - сила,
стремящаяся вернуть точку в положение
равновесия (всегда направлена к положению
равновесия и зависит от величины отклонения
точки от положения равновесия х).
Сила сопротивления R, зависящая от
скорости движения
Возмущающая сила, т.е. сила, являющаяся
заданной функцией времени.
Fх cx
Rх x
11. ДИНАМИКА ТОЧКИ
16.3ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Свободные прямолинейные колебания материальной
точки
Восстанавливающая
сила
если
c/m = k2,
то
x k 2 x 0
Fх cx
m x Fx ,
или
m x сx
дифференциальное уравнение
свободных колебаний
при отсутствии сопротивления.
12. ДИНАМИКА ТОЧКИ
x16.4
ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Свободные прямолинейные колебания материальной
точки
x k 2 x 0
Характеристическое
уравнение:
Пусть
C1 = Acos ,
C2 = Asin ,
х = А (sin kt cos + cos kt sin )
или
x = ent
n2 + k2 = 0, n1,2 = ± ik
общее решение
x = C1 sin kt + C2 cos kt,
закон гармонических колебаний точки:
x = Asin (kt + ).
Скорость точки:
vx = Ak cos (kt + ).
13. ДИНАМИКА ТОЧКИ
16.5ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Свободные прямолинейные колебания материальной
точки
x = A sin (kt + )
A - амплитуда колебаний.
(kt+ )= - фаза колебаний.
- начальная фаза колебаний.
k - круговая частота колебаний
Период колебаний Т промежуток времени, в течение
которого точка совершает одно
полное колебание
T = 2 /k.
Частота колебаний ν – число
колебаний, совершаемых за 1с
= 1/T = k/2 .
14. ДИНАМИКА ТОЧКИ
16.6ДИНАМИКА ТОЧКИ
Дифференциальные уравнения движения
материальной точки
Влияние постоянной силы на свободные колебания
точки
точка равновесия
( P F )
Fx = - с(х + ст)
В результате
const
m x cx
или
статическое отклонение
P= const
F = cx
В точке равновесия при x=
F=P = с ст
x k 2 x 0
ст
Т 2 m cт / P
15. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
17.2ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
Введение в динамику системы
Механическая система - совокупность материальных точек или
тел, находящихся в механическом взаимодействии
Fke - Внешние силы, действующие на точки системы со стороны
точек или тел, не входящих в состав данной системы
Fki - Внутренние силы, с которыми точки или тела данной системы
действуют друг на друга
Свойства внутренних сил:
Fki
0
i
m
(
F
0 k ) 0
16. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
17.3ОБЩИЕ
ТЕОРЕМЫ
ДИНАМИКИ
ТЕОРЕМА О ДВИЖЕНИИ
ЦЕНТРА
МАСС
Центр масс механической системы
Масса системы: M mk
Центром масс (центром инерции) механической системы называется
геометрическая точка С, координаты которой :
mk xk
xС
M
mk yk
уС
M
Радиус-вектор центра масс:
mk zk
zC
M
mk rk
rC
M
17. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
17.4ТЕОРЕМА
О ДВИЖЕНИИ ЦЕНТРА МАСС
Для каждой точки системы
mk ak Fke Fki
mk a k Fke Fki
d 2 rk
d 2 rC
mk 2 M 2
dt
dt
mk rk
rC
M
mk rk MrC
mk a k MaC
aC — ускорение центра
масс системы
Мa C Fke
d 2 хC
e
M
F
kx
2
dt
d 2 уC
e
M
F
kу
2
dt
d 2 zC
e
M
F
kz
2
dt
Дифференциальные уравнения
движения центра масс в проекциях
на оси координат
18. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
17.5ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
Мa C Fke
Закон сохранения движения
центра масс
1. Пусть сумма внешних сил, действующих на систему, равна нулю
e
F
k 0
aC 0
vC сonst
2. Пусть сумма внешних сил системы, не равна нулю, но сумма их
проекций на какую-нибудь ось равна нулю
Fke 0
Fkхe 0
М x C 0
x C 0
x C vCx const
19. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
17.6ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
Примеры применения теоремы о
движении центра масс
Действие пары сил на тело
Fke F F ' 0
aC 0
vC сonst v0C 0
Движение по горизонтальной плоскости
Fтр
F
F’
20. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
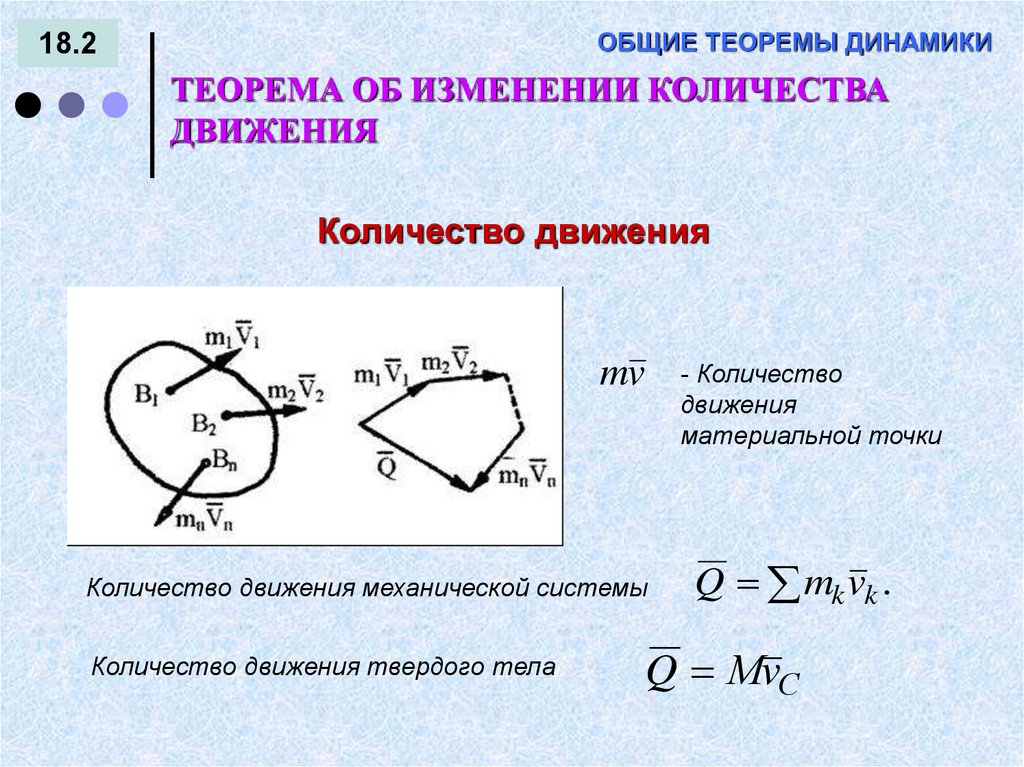
18.2ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
Количество движения
mv
- Количество
движения
материальной точки
Количество движения механической системы
Количество движения твердого тела
Q mk vk .
Q МvС
21. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
18.3ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
Импульс силы
Элементарный импульс силы:
dS Fdt
Импульс силы за конечный промежуток времени t1:
t1
S F dt .
0
Проекции импульса на координатные оси
t1
t1
t1
S у Fу dt .
S x Fx dt.
S z Fz dt.
0
0
0
Единицей измерения импульса силы в системе СИ является 1
кг м/с = 1 Н/с.
22. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
18.4ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
Дифференциальное уравнение движения точки
t1
d ( mv )
Fk .
dt
mv mv0 Fk dt.
0
mv mv0 Sk
Теорема об изменении количества
движения материальной точки
mv1x mv0 x S kx ,
mv1 y mv0 y S ky ,
mv1z mv0 z S kz.
23. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
18.5ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
mk a k Fke Fki
Для всех точек механической системы
d m v dQ .
m
a
k k
k k
dt
dt
=0
Теорема об изменении количества движения системы:
dQ
Fke .
dt
t1
Q1 Q0
0
Fke dt
dQ y
dQx
dQz
e
e
Fkx ,
Fkze .
Fky ,
dt
dt
dt
Q1 Q0
e
Sk
e
Q1x Qox S kx
e
Q1 y Qoy S ky
e
Q1z Qoz S kz
24. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
17.10ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
Закон сохранения количества
движения
1.
2.
Fke
0.
Fkхe
0.
dQ
Fke 0
dt
dQx
e
Fkx
0
dt
Q const
Qх const
25. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
19.2ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
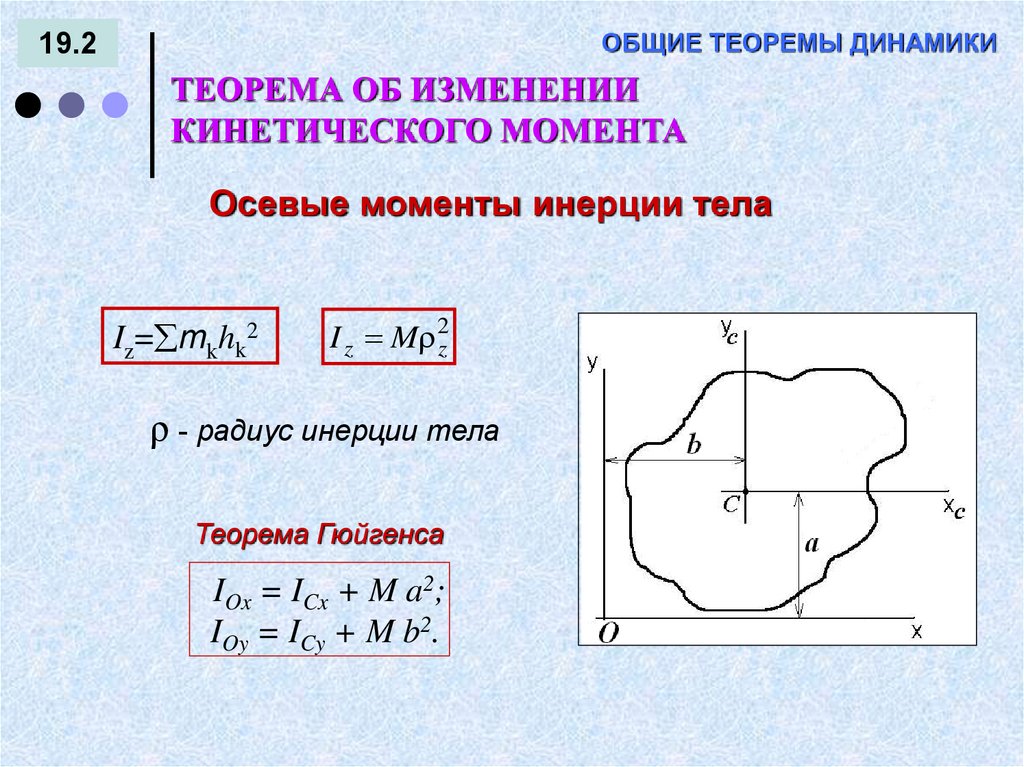
Осевые моменты инерции тела
Iz= mkhk2
I z M 2z
ρ - радиус инерции тела
Теорема Гюйгенса
IOx = ICx + M a2;
IOy = ICy + M b2.
26. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
19.3ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
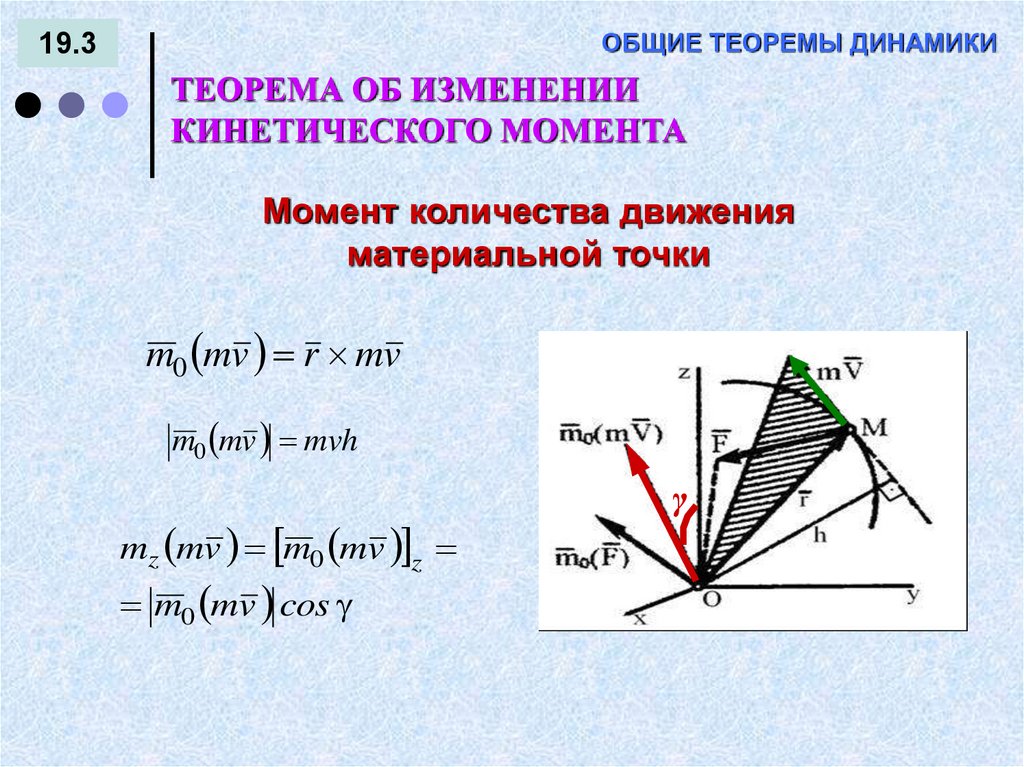
Момент количества движения
материальной точки
m0 mv r mv
m0 mv mvh
mz mv m0 mv z
m0 mv cos
γ
27. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
19.4ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
Теорема об изменении
момента количества движения точки
d r mv dr mv r m dv v mv r ma .
dt
dt
dt
v mv 0
d
r mv r F
dt
d
m0 (mv ) m0 ( F )
dt
или
28. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
20.2ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
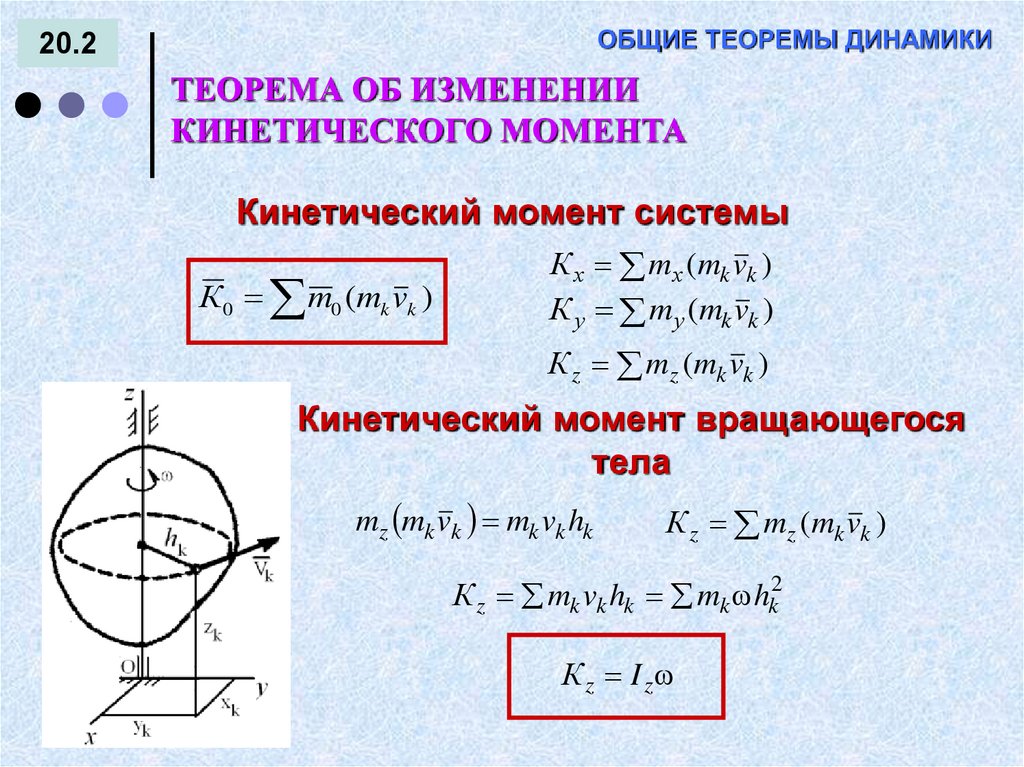
Кинетический момент системы
К 0 m0 (mk vk )
К х mх (mk vk )
К у mу (mk vk )
К z mz (mk vk )
Кинетический момент вращающегося
тела
mz mk vk mk vk hk
К z mz (mk vk )
К z mk vk hk mk hk2
К z I z
29. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
20.3ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
Если рассмотреть одну точку системы:
d [m (m v )] m ( F e ) m ( F i ) ,
0
k k
0 k
0 k
dt
для всех точек системы:
=0
d [ m ( m v )] m ( F e ) m ( F i ).
0 k k
0 k 0 k
dt
dK 0
m0 ( Fke )
dt
Теорема об изменении кинетического
момента механической системы
dK x
mx ( Fke )
dt
dK y
my ( Fke )
dt
dK z
mz ( Fke )
dt
30. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
20.4ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
следствия из теоремы:
dK 0
m0 ( Fke )
dt
dK z
mz ( Fke )
dt
1. Если сумма моментов всех внешних сил, действующих на
систему, относительно центра О равна нулю
m0 ( Fke ) 0
то
K0 const
2. Если сумма моментов всех внешних сил, действующих на
систему, относительно некоторой неподвижной оси равна нулю
mz ( Fke ) 0
то
Kz = const
31. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
20.5ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
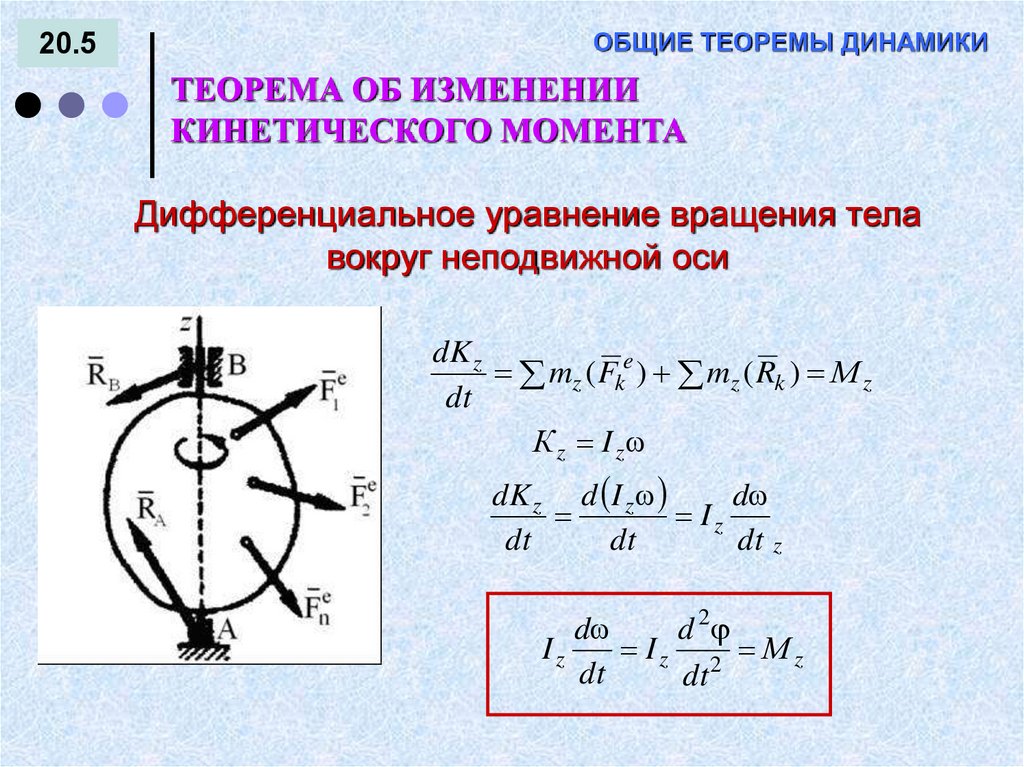
Дифференциальное уравнение вращения тела
вокруг неподвижной оси
dK z
mz ( Fke ) mz ( Rk ) М z
dt
К z I z
dK z d I z
d
Iz
dt
dt
dt z
d
d 2
Iz
Iz 2 М z
dt
dt
32. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
21.3ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ
ЭНЕРГИИ
Работа силы. Мощность
Элементарная работа силы
dA = F ds,
где
F = F cos ,
dA = Fds cos .
Работа силы на конечном перемещении
1. ( F const)
( M1 )
A( M 0 M1 ) F ds
(M 0 )
2. ( F const)
A( M 0 M1 ) F s1 Fs1cos
33. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
21.4ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Работа силы. Мощность
Если вектор силы спроецировать на оси координат
( M1 )
A( M 0 M1 ) ( Fx dx Fy dy Fz dz)
(M 0 )
Единицей измерения работы в системе СИ является - 1 джоуль
(1 Дж = 1H м = 1 кг м2 /с2).
Мощность - это величина, определяющая работу, совершаемую
силой в единицу времени.
N = dA/dt = F ds/dt = F v.
Единицей измерения мощности в системе СИ является ватт
(1 Вт = 1Дж/с). В технике - 1 л.с. = 736 Вт.
34. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
21.5ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Примеры вычисления работы
Работа силы тяжести
z1
A( M 0 M1 ) ( P)dz P( z0 z1 )
z0
z0 - z1 = h
A( M 0 M1 ) Р h
Работа силы тяжести не зависит от формы траектории точки её
приложения. Силы, обладающие таким свойством, называются
потенциальными силами.
35. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
21.6ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Работа силы. Мощность
Работа силы упругости
F = cλ = c x
и
Fx = -cx.
x1
c
A( M 0 M1 ) ( cx)dx ( x02 x12 ).
2
x0
A( M 0 M1 )
с 2
( 0 21 ) ,
2
36. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
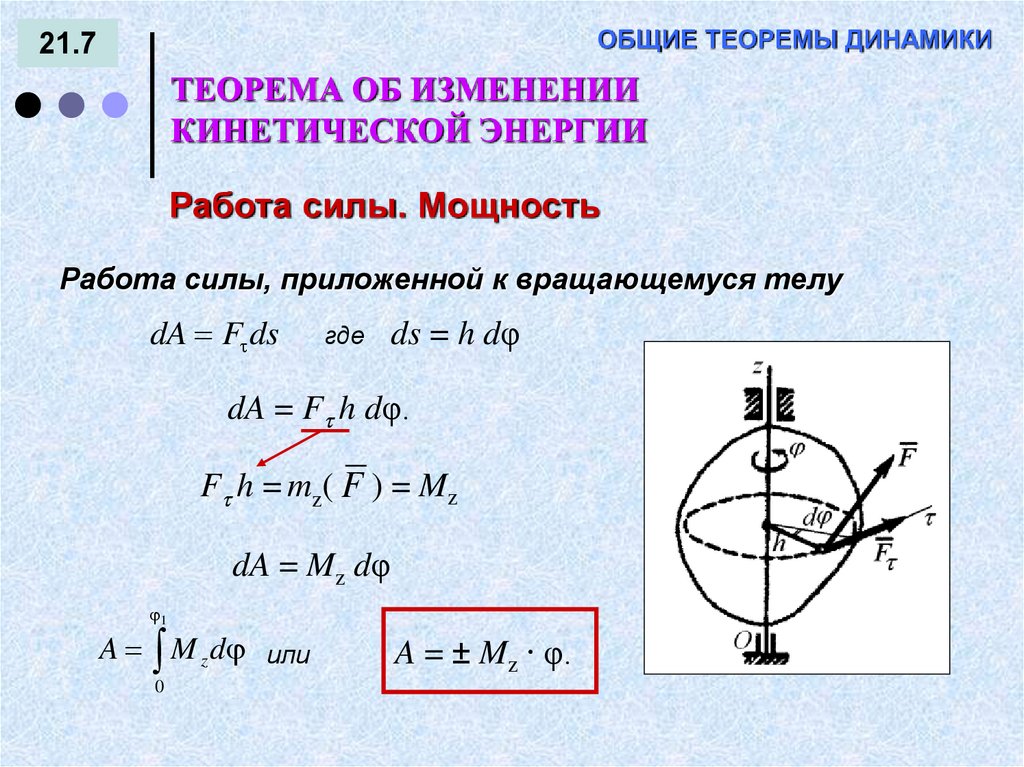
21.7ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Работа силы. Мощность
Работа силы, приложенной к вращающемуся телу
dA F ds
где
ds = h dφ
dA = F h dφ.
F h = mz( F ) = Mz
dA = Mz dφ
1
A M z d или
0
A = ± Mz ∙ φ.
37. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
22.2ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ
ЭНЕРГИИ
Кинетическая энергия
для материальной точки
для механической системы
из n материальных точек
M
V
v2
m
2
vk2
T mk
2
k 1
n
Кинетическая энергия - скалярная величина
Единица измерения кинетической энергии в системе СИ - 1 Дж.
38. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
22.3ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Кинетическая энергия
для твердого тела
Поступательное движение
Вращательное движение
2
T Iz
2
vС2
М
2
Плоскопараллельное движение
2
Tпл I P
2
v2
2
Tпл M
Iс
2
2
39. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
22.4ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Рассмотрим материальную точку с массой m
ma = Fk .
M
a
dv dv ds
dv
v
dt ds dt
ds
V
dv
mv Fk
ds
mv 2
d(
) dAk
2
теорема об изменении
кинетической энергии точки
в дифференциальной форме
mvdv dAk
mv12 mv02
А(М0М1 )
2
2
теорема об изменении
кинетической энергии точки
в конечном виде
40. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
22.5ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Рассмотрим материальную точку механической системы с массой mk
d(
mk v 2k
2
) dAek dAik
Для всей механической системы
dT dAek dAik
теорема об изменении
кинетической энергии системы
в дифференциальной форме
d (
mk v 2k
2
) dAek dAik
T Т 0 Aek Aik
теорема об изменении
кинетической энергии системы
в интегральной форме































 physics
physics








