Динамика материальной точки. (Лекция 1)

1. Динамика материальной точки

Динамика материальной
Динамика есть раздел теоретической (классической) механики,
точки
который изучает движение материальных тел и их систем под
действием приложенных к ним сил.

2. Аксиомы динамики материальной точки

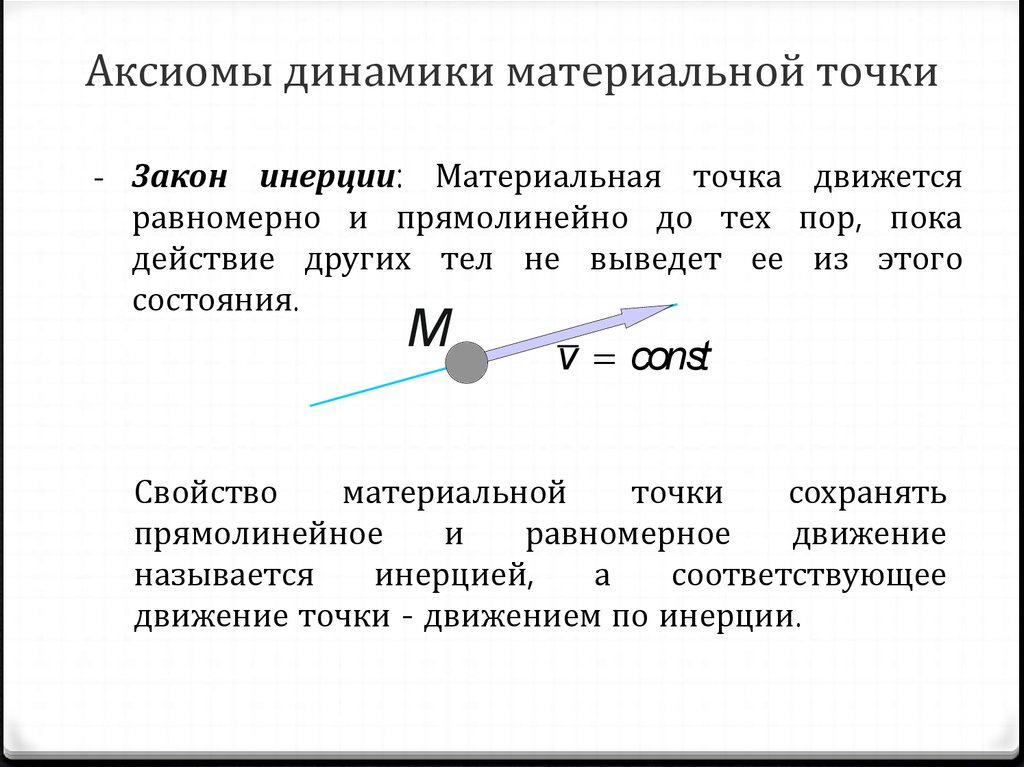
- Закон инерции: Материальная точка движется
равномерно и прямолинейно до тех пор, пока
действие других тел не выведет ее из этого
состояния.
M
v const
Свойство
материальной
точки
сохранять
прямолинейное
и
равномерное
движение
называется
инерцией,
а
соответствующее
движение точки - движением по инерции.

3. Аксиомы динамики материальной точки

Второй закон Ньютона (основное уравнение
динамики материальной точки): Ускорение, которое
материальная точка получает под действием
приложенной к ней силы, имеет то же направление,
что и силы, и по величине пропорционально силе.
M
mw F
Масса есть мера инертности точки – чем больше
масса точки, тем большая нужна сила, чтобы
изменить скорость этой точки.

4. Аксиомы динамики материальной точки

Закон равенства действия и противодействия:
Силы, с которыми взаимодействуют две материальные
точки, имеют равную величину, общую линию действия
и противоположное направление.
M2
F2
F1
F1 F2
M1
Этот закон выполняется при взаимодействии тел,
если они соприкасаются в одной точке. Если
взаимодействие тел происходит по поверхности или в
некотором объеме, то оно не будет сводиться к одной
силе.

5. Аксиомы динамики материальной точки

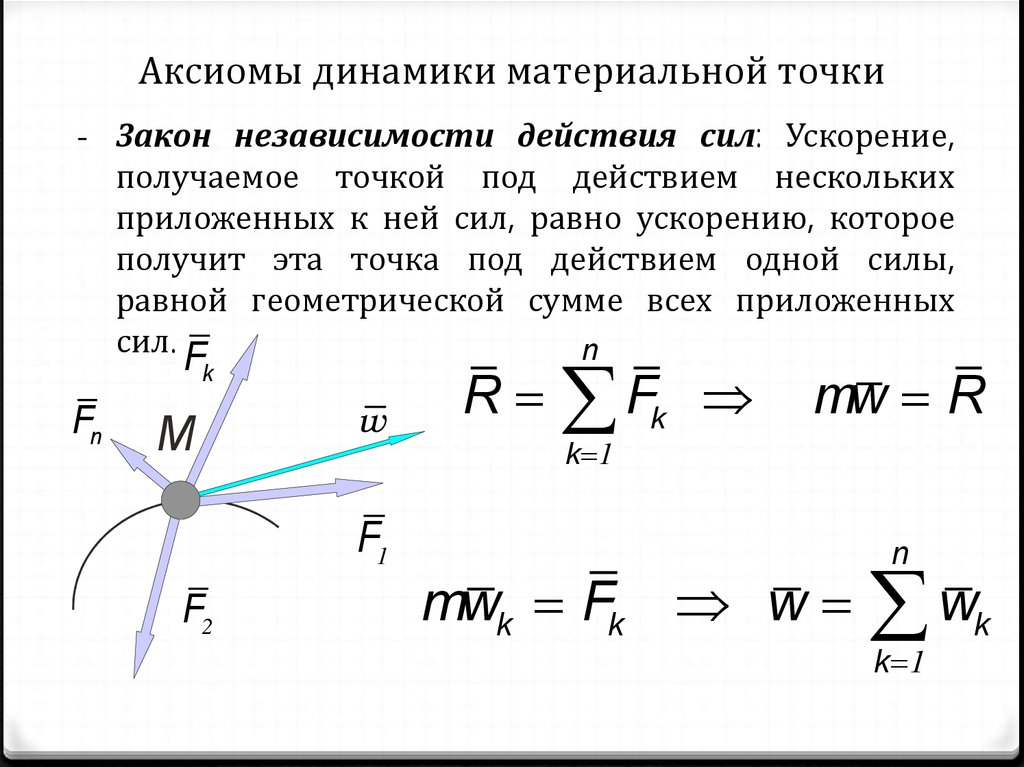
- Закон независимости действия сил: Ускорение,
получаемое точкой под действием нескольких
приложенных к ней сил, равно ускорению, которое
получит эта точка под действием одной силы,
равной геометрической сумме всех приложенных
сил.
n
Fk
Fn
R
M
k 1
F1
F2
F
k
mw R
mwk Fk w
n
w
k 1
k

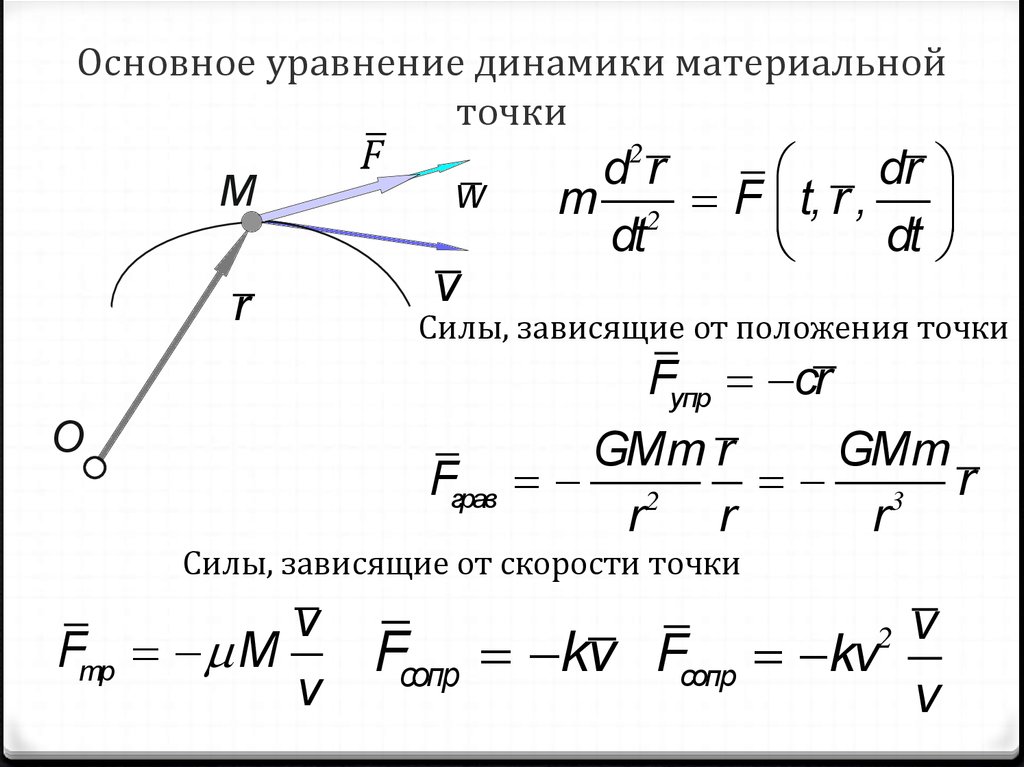
6. Основное уравнение динамики материальной точки

dr
dr
m 2 F t, r ,
dt
dt
2
M
r
w
v
Силы, зависящие от положения точки
Fупр cr
O
Fграв
GMm r
GMm
2
3 r
r
r
r
Силы, зависящие от скорости точки
v
Fтр M
v
Fсопр kv Fсопр
v
kv
v
2

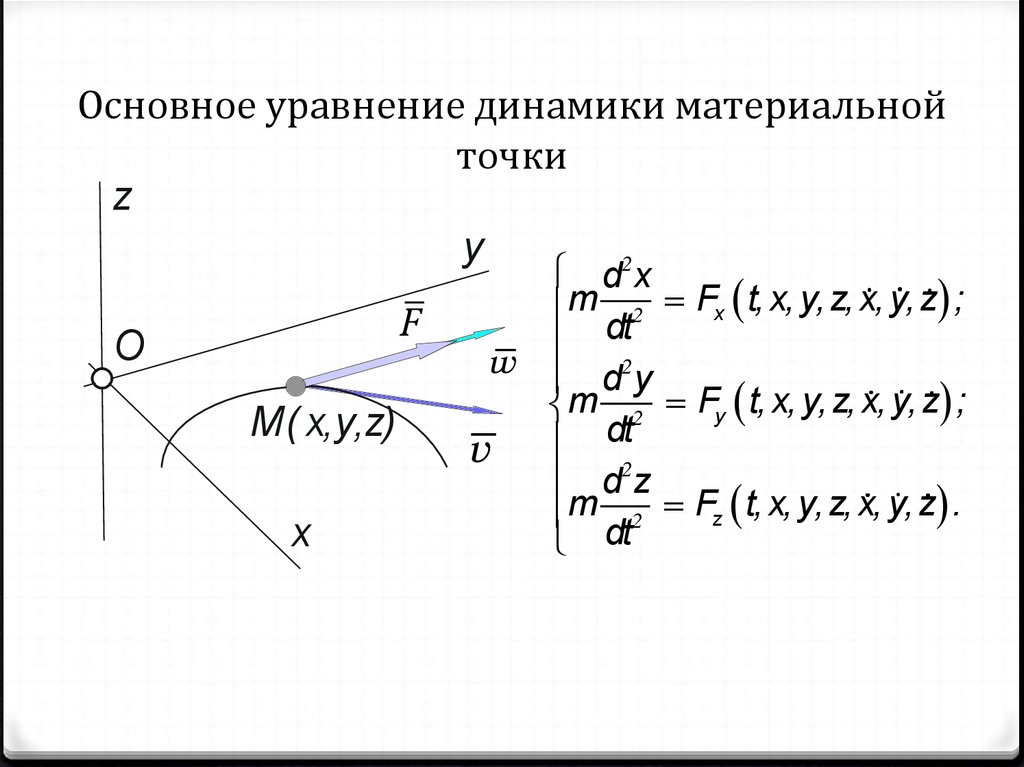
7. Основное уравнение динамики материальной точки

z
y
2
O
M( x,y,z)
x
dx
m 2 Fx t, x, y, z, x, y, z ;
dt2
dy
m 2 Fy t, x, y, z, x, y, z ;
dt
d2z
m 2 Fz t, x, y, z, x, y, z .
dt

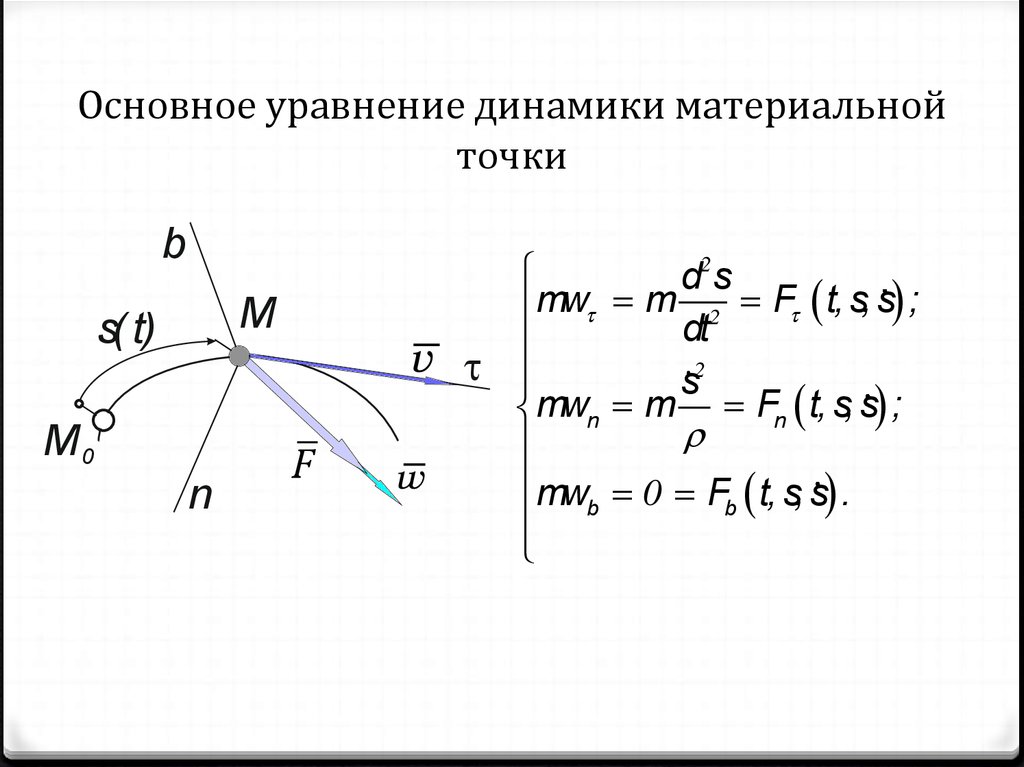
8. Основное уравнение динамики материальной точки

b
M
s( t)
M0
n
d2 s
mw m 2 F t, s, s ;
dt
s2
mwn m Fn t, s, s ;
mw 0 F t, s, s .
b
b

9. Основные задачи динамики материальной точки

Первая или прямая задача: Известно движение
материальной точки, требуется определить силы,
вызывающие это движение.
r r t
F t, r , r ?
F t, r , r mw.
Для решения этой задачи достаточно найти
ускорение точки, т.е. решить основную задачу
кинематики.

10. Пример решения прямой задачи динамики

x acoskt;
y bsinkt.
2
F
t
mw
mak
coskt;
x
x
2
Fy t mwy mbk sinkt.
2
2
Fx t mk acoskt mk x;
2
2
F
t
mk
bsinkt
mk
y.
y
F mk r cr
2

11. Основные задачи динамики материальной точки

Вторая или обратная задача: Известны силы,
действующие на точку, требуется определить
движение этой точки.
F F t, r , r ,
r t ?
dr
dr
m 2 F t, r ,
dt
dt
2
Решение этой задачи сводится к составлению и
интегрированию дифференциальных уравнений
движения материальной точки.

12. Пример решения обратной задачи динамики

M
w r 2r 0
d
2
r 2r
r 0
dt
O
r const
2
r v
rv c const

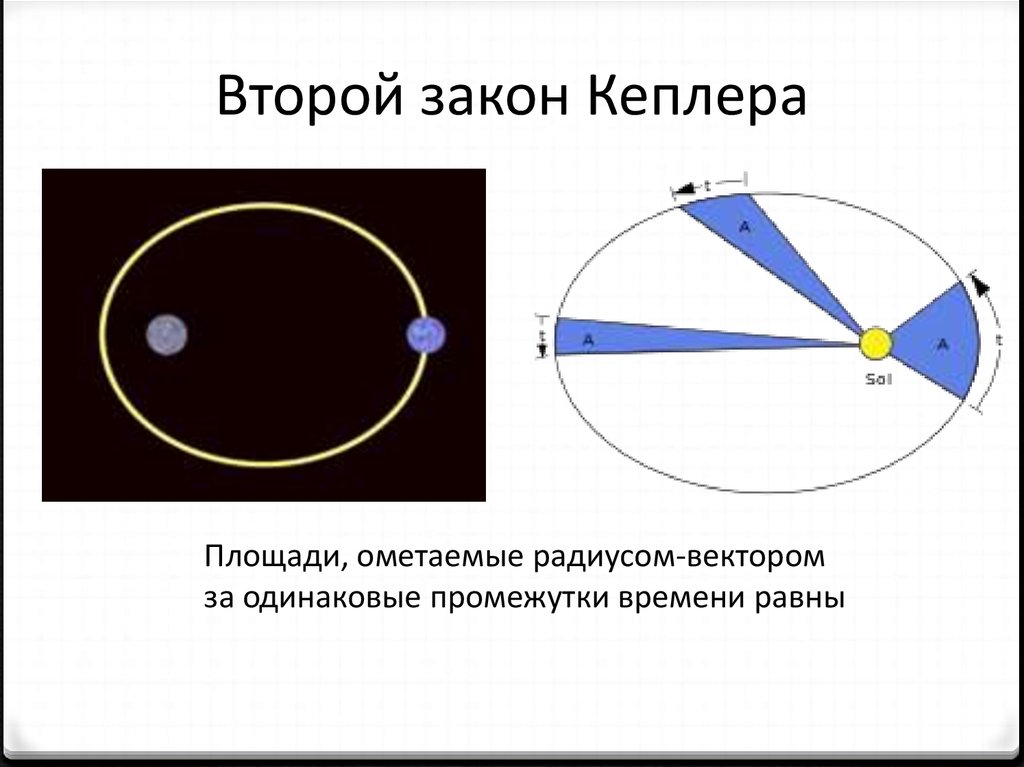
13.

Второй закон Кеплера
Площади, ометаемые радиусом-вектором
за одинаковые промежутки времени равны

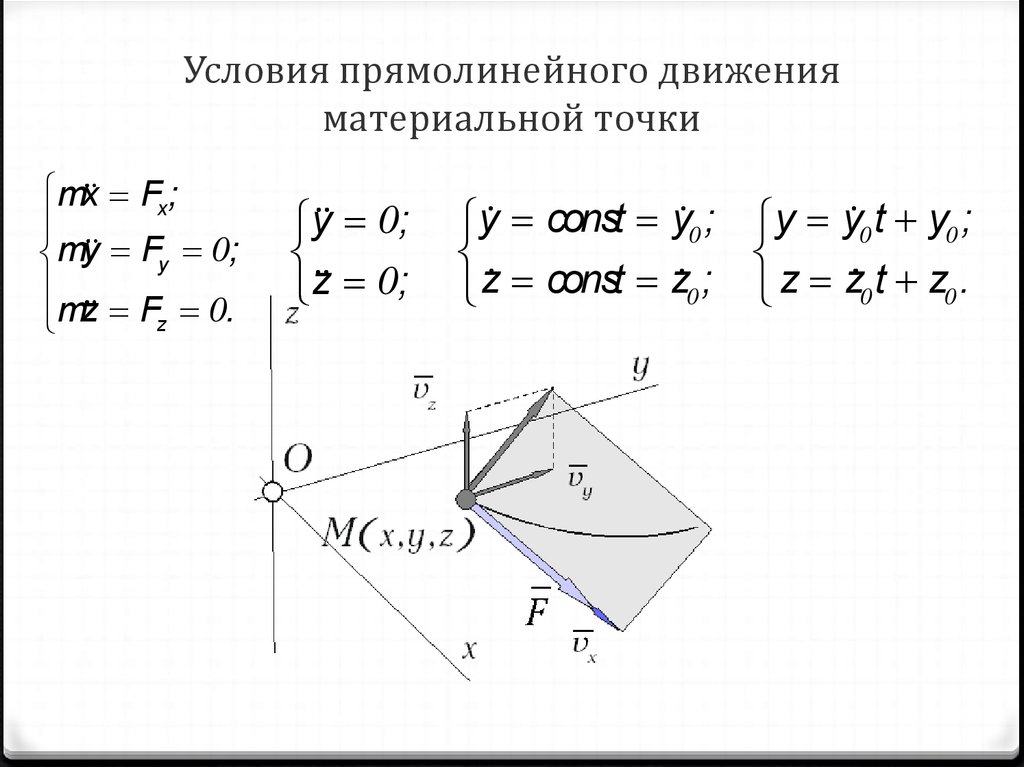
14. Условия прямолинейного движения материальной точки

z
y
O
M( x,y,z)
x
x t x t ;
y t 0;
z t 0.
Fx mx;
Fy my 0;
Fz mz 0.

15. Условия прямолинейного движения материальной точки

mx Fx;
my Fy 0;
mz Fz 0.
y 0;
z 0;
y const y0 ; y y0 t y0 ;
z const z0 ; z z0 t z0 .

16. Условия прямолинейного движения материальной точки

Материальная
точка
будет
совершать
прямолинейное движение, если сила, действующая
на нее, имеет неизменное направление, совпадающее
с направлением начальной скорости.