Similar presentations:
Динамика точки. Законы Галилея – Ньютона
1. ДИНАМИКА ТОЧКИ. ЗАКОНЫ ГАЛИЛЕЯ – НЬЮТОНА
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.ДИНАМИКА
ЛЕКЦИЯ 2
2. ДИНАМИКА
это раздел теоретической механики, в которомустанавливается и изучается связь между
движением материальных тел и
действующими на них силами
I.
Движение тела задано и требуется найти силы под
действием которых это движение происходит.
II. Силы, действующие на тело, заданы и требуется
найти закон движения тела.
2
Введение
3. ДИНАМИКА
Динамикаматериальной
точки
Динамика
механической
системы
Под материальной точкой подразумевается тело,
размерами и различаем в движениях отдельных точек
которого можно пренебречь.
3
Введение
4. ИСТОРИЯ 1 ЗАКОНА НЬЮТОНА
Аристотель384 до н. э. — 322 до н. э.
4
Законы Ньютона
Круговое движение - это самое
совершенное движение,
присущее только небесному
миру.
Естественное движение- это
движение тяжёлого тела вниз к
центру Мира, к центру Земли, и
лёгкого вверх.
Все остальные движения на
Земле насильственные и могут
происходить только под
действием внешних сил
«Всё, что находится в движении,
движется благодаря воздействию
другого»
Нет сил – нет движения
5. ИСТОРИЯ 1 ЗАКОНА НЬЮТОНА
Принцип относительности:«Для предметов, захваченных
равномерным движением, это последнее
как бы не существует и проявляет своё
действие только на вещах, не
принимающих в нём участия»
Галилей
1564 — 1642
5
Законы Ньютона
Все процессы в инерциальных
системах отсчёта протекают одинаково,
независимо от того, неподвижна ли
система или она находится в состоянии
равномерного и прямолинейного
движения
6. ИСТОРИЯ 1 ЗАКОНА НЬЮТОНА
Принцип инерции:при отсутствии внешних сил тело либо
покоится, либо равномерно движется
Галилей
1564 — 1642
6
Законы Ньютона
7. ИСТОРИЯ 1 ЗАКОНА НЬЮТОНА
Ньютон1643 — 1727
7
Законы Ньютона
8. ИСТОРИЯ 1 ЗАКОНА НЬЮТОНА
1 ЗАКОН НЬЮТОНА«Всякое тело продолжает удерживаться в состоянии покоя
или равномерного и прямолинейного движения, пока и
поскольку оно не понуждается приложенными силами
изменить это состояние»
Существуют такие системы отсчёта,
называемые инерциальными, относительно
которых материальные точки, когда на них не действуют
никакие силы, находятся в состоянии покоя
или равномерного прямолинейного
движения
8
Законы Ньютона
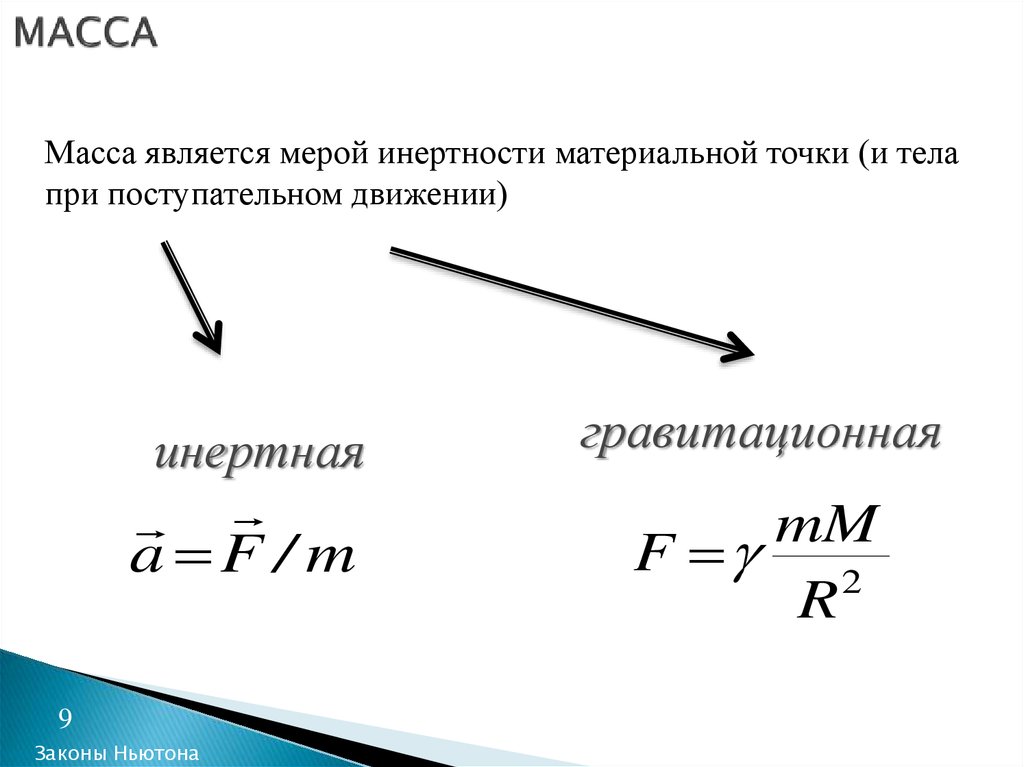
9. МАССА
Масса является мерой инертности материальной точки (и телапри поступательном движении)
инертная
a F / m
9
Законы Ньютона
гравитационная
mM
F
2
R
10. 2 ЗАКОН НЬЮТОНА
«Изменение количества движения пропорциональноприложенной движущей силе и происходит по направлению той
прямой, по которой эта сила действует»
В инерциальных системах отсчёта ускорение,
приобретаемое материальной точкой, прямо
пропорционально вызывающей его силе, совпадает с ней
по направлению и обратно пропорционально массе
материальной точки
a F / m
10
Законы Ньютона
ma F
n
ma Fk F
k 1
11. 2 ЗАКОН НЬЮТОНА В ДЕКАРТОВОЙ СИСТЕМЕ ОТСЧЕТА
nma Fk F
k 1
ma
F
, ma F , ma F
x
x
y
y
z
z
a
x , a
x
y
y , a
z
z
m x F , m y F , m z F
x
y
z
11
2 закон Ньютона
12. 2 ЗАКОН НЬЮТОНА В ЕСТЕСТВЕННОЙ СИСТЕМЕ ОТСЧЕТА
bn
a a an n abb
a s a s 2
n
12
2 закон Ньютона
ab 0
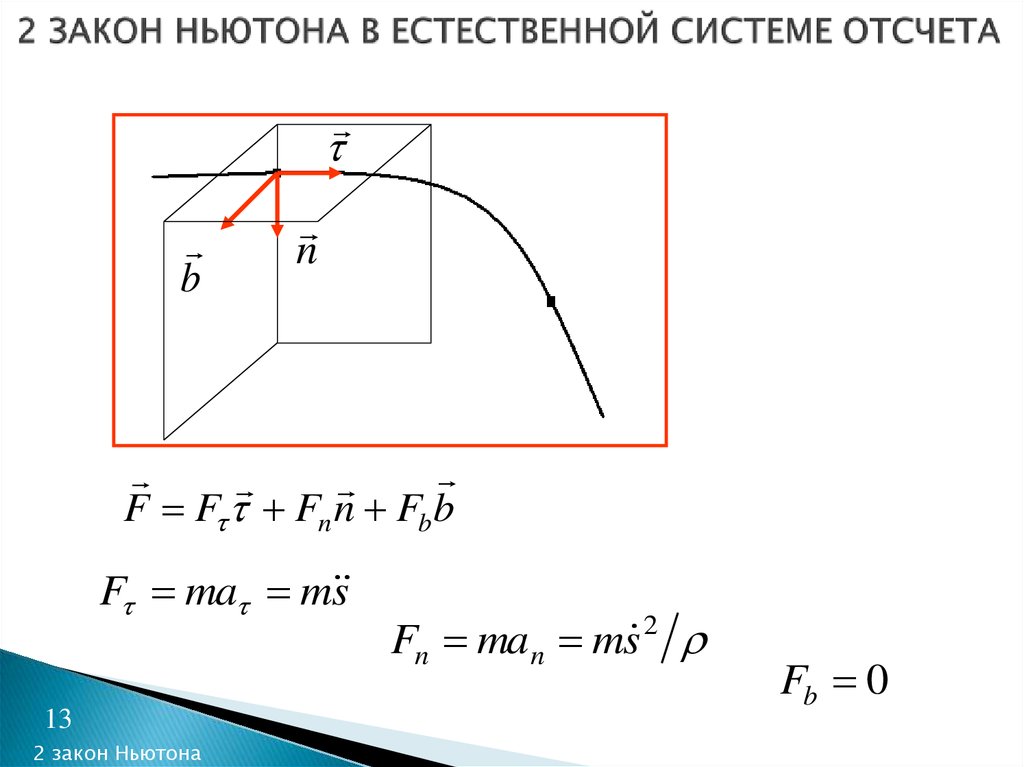
13. 2 ЗАКОН НЬЮТОНА В ЕСТЕСТВЕННОЙ СИСТЕМЕ ОТСЧЕТА
bn
F F Fn n Fbb
F ma m s
13
2 закон Ньютона
Fn ma n ms 2
Fb 0
14. СИСТЕМЫ ОТСЧЕТА
Геоцентрическая система отсчета —система отсчета,связанная с Землей.
Гелиоцентрическая система отсчета —система отсчета,
связанная с Солнцем, причем оси коордитнат
направлены к неподвижным звездам
14
2 закон Ньютона
15. ПРИМЕР РЕШЕНИЯ 1 ЗАДАЧИ ДИНАМИКИ
Точка массой m движется в плоскости х,у по закону х=2sin((π/6)t),у=2cos((π/6)t). Найти силу, под действием которой происходит это
движение.
x
2
18
sin(
6
y
t ),
2
18
cos(
15
2 закон Ньютона
6
t)
y
m 2
Fx
sin( t ),
18
6
m 2
Fy
cos( t )
18
6
F
M
F
О
x
2
-2
Fx Fy
2
2
m 2
const
18
16. РЕШЕНИЕ 2 ЗАДАЧИ ДИНАМИКИ
m x Fx (t, x, y,z, x , y , z )m y Fy (t, x, y,z, x , y , z )
x x (t, C1, . ,C6 )
m z Fz (t, x, y,z, x , y , z )
z z (t, C1, . ,C6 )
y y (t, C1, . ,C6 )
Постоянные С1, …. , С6 находятся из начальных
условий
В качестве начальных условий следует задать
положение и скорость материальной точки в
начальный момент времени.
16
2 закон Ньютона
17. РЕШЕНИЕ 2 ЗАДАЧИ ДИНАМИКИ
Самолет летит на высоте 400м со скоростью 200 м/с. Найтизакон движения груза, сброшенного с самолета.
Сопротивлением воздуха пренебречь.
Рассмотрим движение груза, считая его материальной точкой
y
m x 0,
x 0,
V0
mg
x C1 ,
х
x C1t C3
17
2 закон Ньютона
m y mg
y g
gt C2
y
t2
y g
C2 t C4
2
18. РЕШЕНИЕ 2 ЗАДАЧИ ДИНАМИКИ
При t = 0x 0,
y 400
x 200,
C1 200
C2 0
y 0
C3 0
Закон движения груза:
x 200 t
2
t
y g
400
2
18
2 закон Ньютона
C4 400
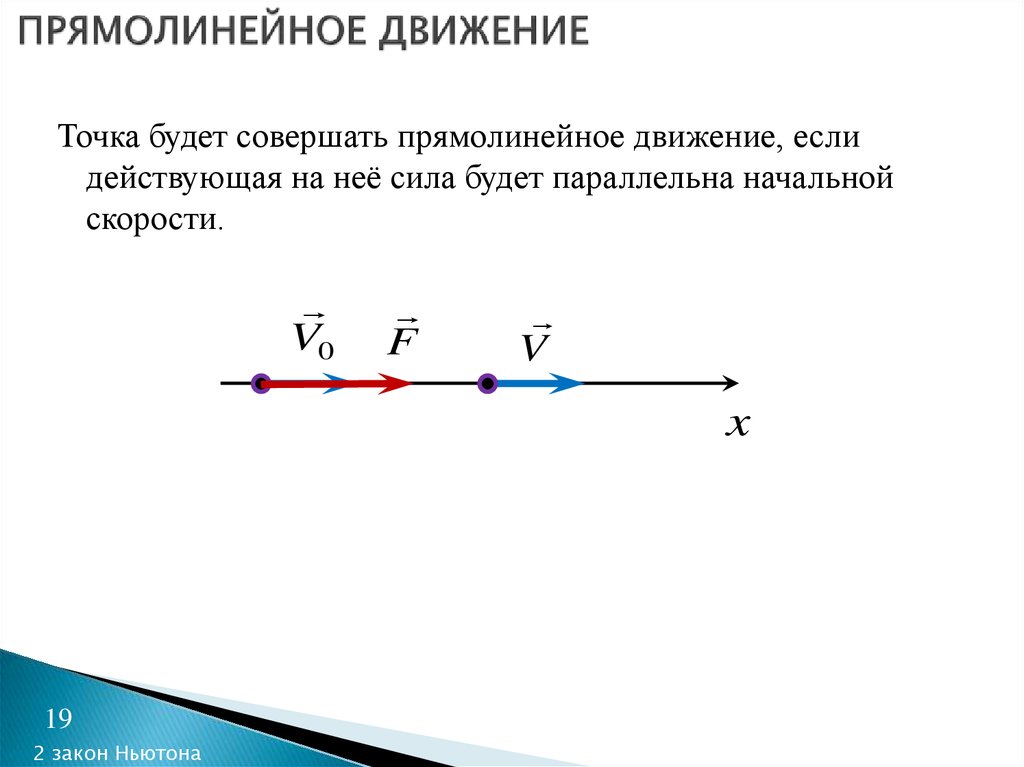
19. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
Точка будет совершать прямолинейное движение, еслидействующая на неё сила будет параллельна начальной
скорости.
V0
F
V
x
19
2 закон Ньютона
20. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
1. Сила зависит от времениm x F (t )
x
F F (t )
dx 1
F (t )
dt m x
1
x F (t )dt C
1
m x
1
x F (t )dt dt C t C
1
2
m x
20
2 закон Ньютона
21. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
F F (V )2. Сила зависит от скорости
m x F (V )
x
dV
x
dt
dV
m
Fx (V )
dt
dV
t m
C ,
1
F (V )
x
21
2 закон Ньютона
dV
dt m
Fx (V )
t (V , C )
1
22. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
3. Сила зависит от координатыm x F (x)
x
F F (x)
dV
dV
dx
dV
x
V
dt dx dt
dx
1
VdV Fx ( x)dx
m
V
2
2
m
F
V
22
2 закон Ньютона
x
( x ) dx C1
2
Fx ( x)dx C1
m
23. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
3. Сила зависит от координатыdx
2
Fx dx C1 ,
dt
m
t
23
2 закон Ньютона
dx
2
Fx dx C1
m
dt
C2
F F (x)
dx
2
Fx dx C1
m



















 physics
physics








