Similar presentations:
Динамика материальной точки. Законы Ньютона
1. Динамика материальной точки Законы Ньютона
Сэр Исааак Ньюатон(1642-1727)—
английский физик,
математик, механик и
астроном, один из
создателей
классической физики.
2.
Ускорение тела или его деформациявызываются нескомпенсированными
воздействиями других тел.
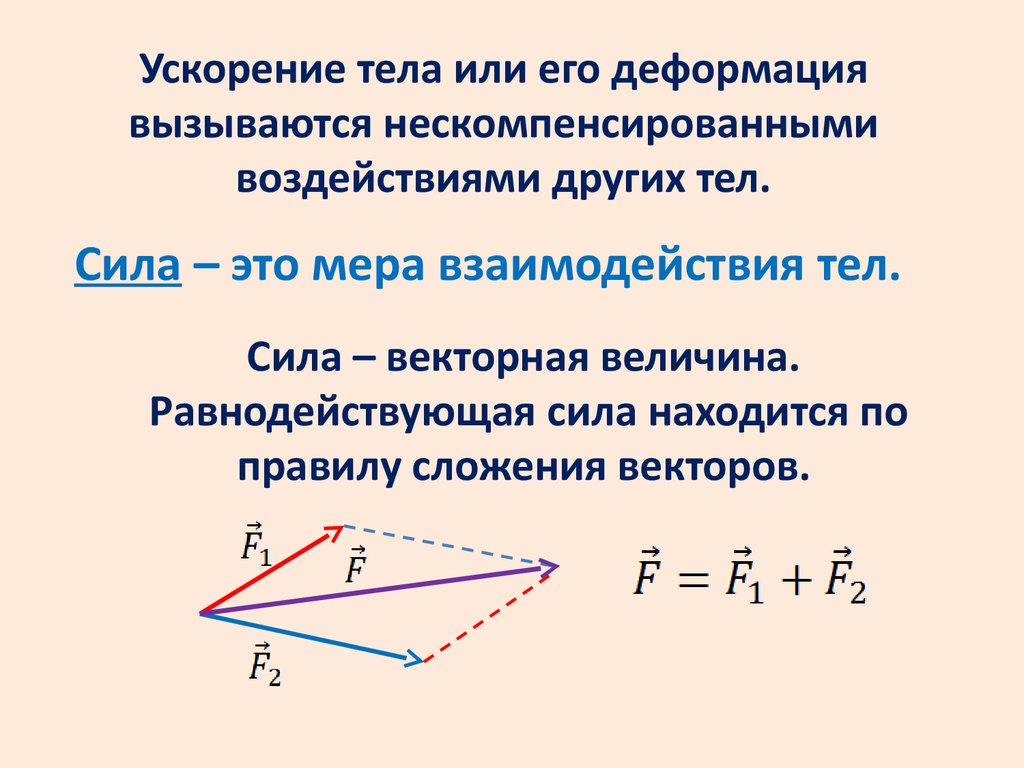
Сила – это мера взаимодействия тел.
Сила – векторная величина.
Равнодействующая сила находится по
правилу сложения векторов.
3.
4.
Первый закон НьютонаСуществуют такие системы отсчёта, называемые
инерциальными,
относительно которых:
если на тело не действует сила или
действие сил скомпенсировано, то это
тело находится в состоянии покоя или
прямолинейного равномерного
движения.
5.
Иначе:в инерциальных системах
отсчета свободное или
квазисвободное тело сохраняет
свою скорость.
6.
При воздействии одной и той же силыразные тела получают разные
ускорения.
Способность тела сохранять скорость
своего движения называется
инертностью .
7.
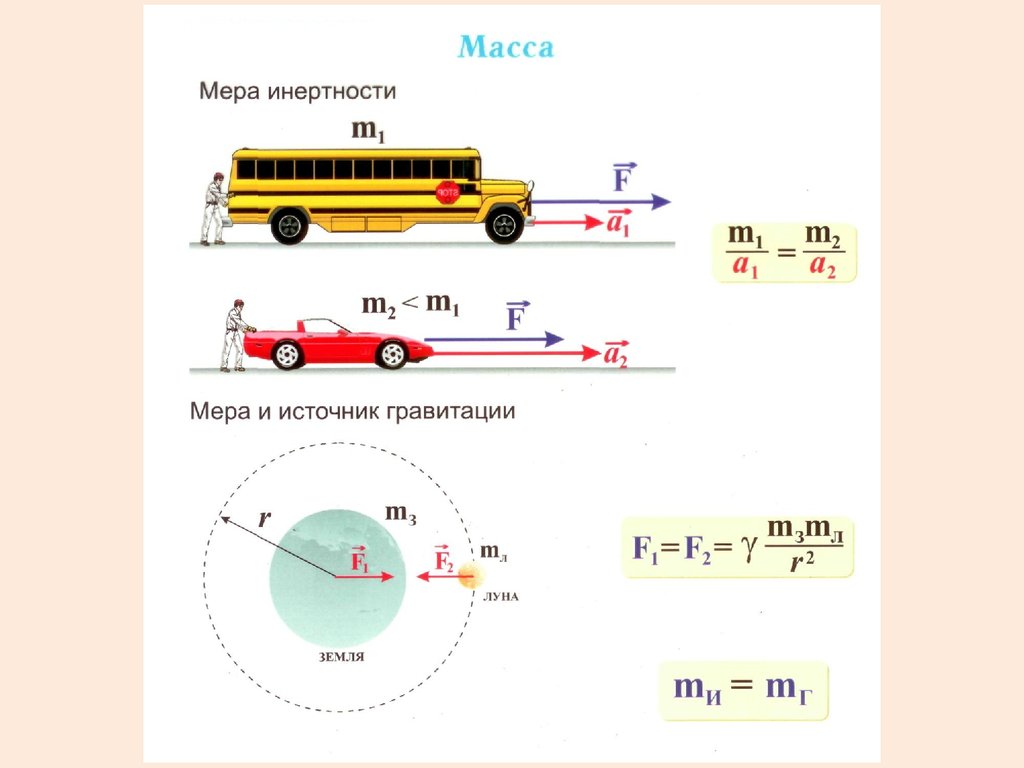
Масса — мера инертности тела припоступательном движении.
Такую массу называют инертной
(mин).
[ mкг
] =[ ]
8.
Масса также является источникомгравитационного взаимодействия тел.
Такую массу называют
гравитационной (mгр).
9.
Закон всемирного тяготения(установлен Ньютоном):
m1m2
F =G 2 .
r
G - гравитационная постоянная
Инертная и гравитационная массы равны.
mин = m гр
10.
11.
12.
Опыт показывает, что:• при воздействии на одно и то же тело
разной силой ускорение, сообщаемое телу,
прямо пропорционально силе;
• если на тела действует одинаковая сила, то
ускорения тел обратно пропорциональны их
массам.
ü
r rï
a~F
ï
ý
1ï
a~ ï
mþ
r
F
r
a=k
m
13.
Полагая k=1, введем единицу измерениясилы 1 Ньютон (Н).
Сила в 1 Н сообщает телу массой 1 кг
ускорение 1м/с2 .
Эталон 1 кг массы, представляет собой
цилиндр из сплава платины (90%) и иридия
(10%) диаметром около 39 мм и такой же
высоты. Масса 1 л воды приблизительно
равна 1 кг.
14.
Второй закон НьютонаВ инерциальной системе отсчета
ускорение, сообщаемое телу, прямо
пропорционально силе, действующей на
тело, и обратно пропорционально массе
этого тела.
r
r F
a=
m
15.
илиr
r
F = ma
Ускорение тела направлено
в сторону действия силы.
16.
Принцип независимости действия силЕсли на МТ действуют несколько сил, то
каждая из них сообщает такое же ускорение,
как если бы других сил не было.
r
å Fi
r
r F
i
a= =
m
m
r
r
a = å ai
i
17.
ИмпульсИмпульсом тела называют
произведение его массы на скорость:
r
r
p = mv
18.
Другая (более общая )форма II-го законаНьютона:
r
r
dv
r
F = ma = m
dt
r
r
r d ( mv ) dp
F=
=
dt
dt
r r
&
F= p
Скорость изменения импульса тела
равна действующей на тело силе.
19.
Чем дольше действует сила и чем онабольше, тем сильнее изменяется
импульс тела:
r r
Dp = F × Dt
Величину справа называют
импульсом силы.
20.
Третий закон НьютонаСилы взаимодействия двух тел равны по
величине, противоположны по направлению
и действуют вдоль одной прямой.
r
r
f12 = - f 21
m1
r
f12
r
f 21
m2
Эти силы приложены к разным телам и не могут
компенсировать друг друга.
21.
ВИДЫ СИЛ В ПРИРОДЕВ настоящее время определено четыре
основных вида взаимодействий.
Вид
Проявление
Радиус действия (м)
Сильное
Ядерные силы
Электромагнитное
Кулоновское
взаимодействие
¥
Слабое
Β-распад
10-18
Гравитационное
Всемирное
тяготение
¥
10-15
Интенсивность взаимодействия убывает сверху вниз.
22.
Механика изучает силыэлектромагнитной и гравитационной
природы
= - kx ,
силы трения F = m N ,
силы сопротивления среды Fv = - k ¢v
Упругие силы Fx
m1m2
Силы тяготения F = G
2 ,
r
r
r
в т.ч. сила тяжести F = mg
23.
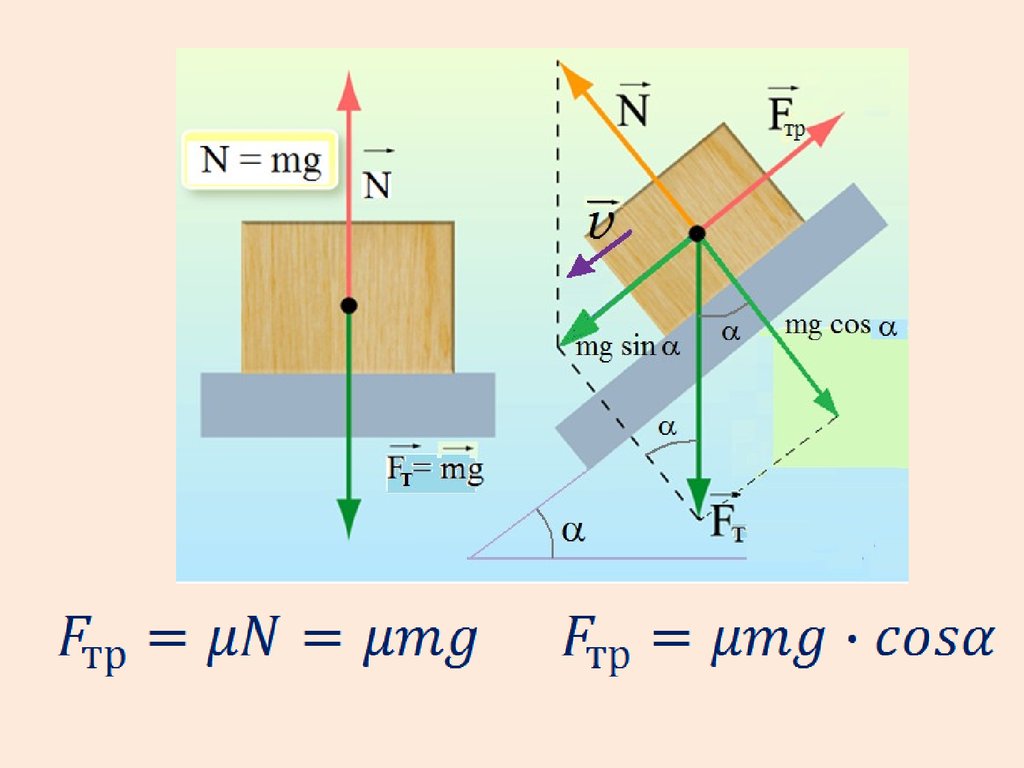
Сила трения – это сила сопротивления,действующая в плоскости касания двух
прижатых друг к другу тел.
Виды трения:
вязкое
24.
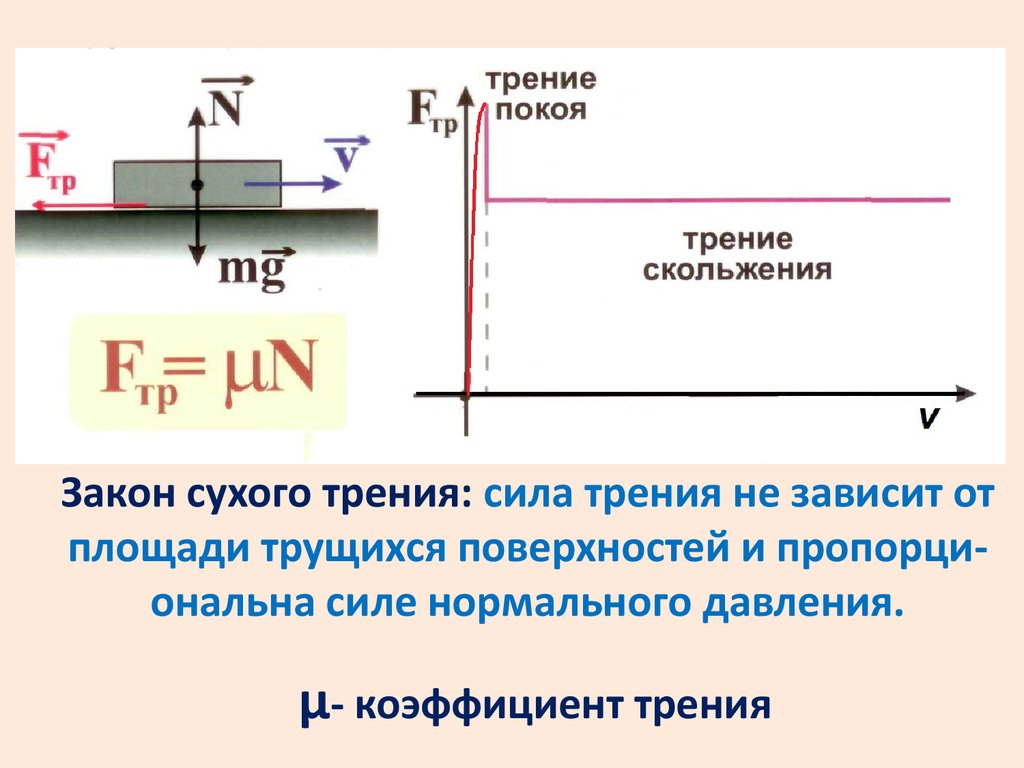
Закон сухого трения: сила трения не зависит отплощади трущихся поверхностей и пропорциональна силе нормального давления.
μ- коэффициент трения
25.
26.
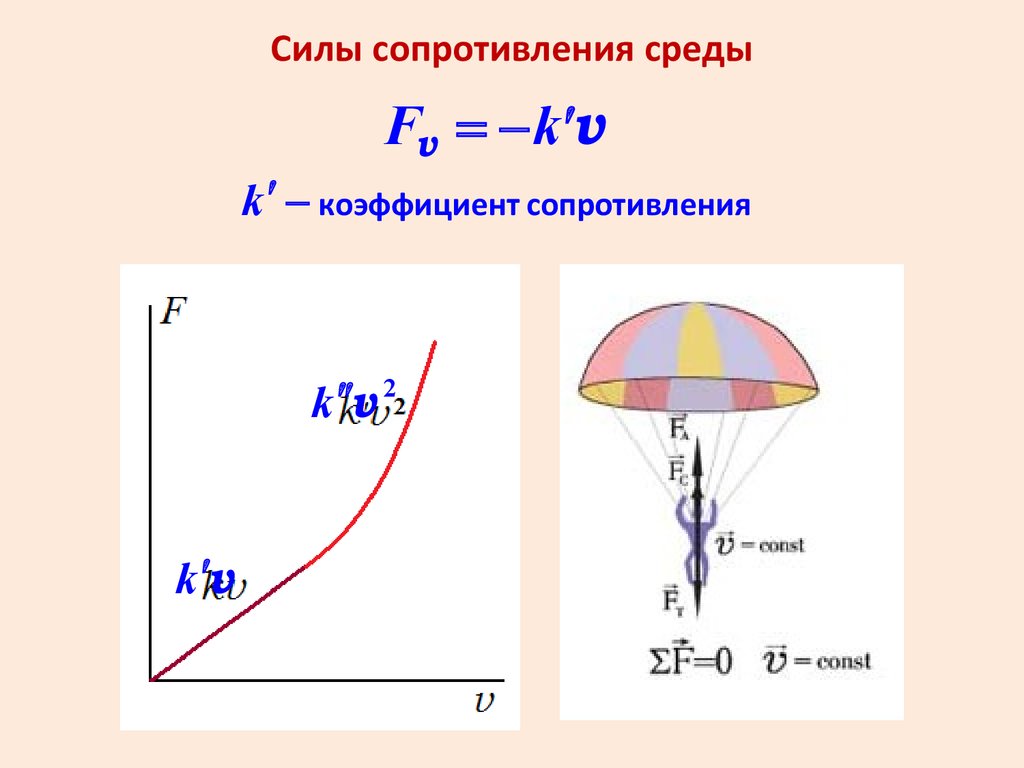
Силы сопротивления средыFv = - k ¢v
k ¢ - коэффициент сопротивления
2
¢¢
k v
k ¢v
27.
Преобразования Галилея.Классический закон сложения
скоростей.
Рассмотрим движение материальной
точки М в двух системах отсчета (СО):
K и K’.
Пусть система K’ равномерно движется
относительно системы К вдоль оси х со
скоростью v0.
28.
ry¢ v
0
y
K
K¢
r
r
r r
r0 = v0t
O
z
z¢
O¢
M
r
r¢
x¢
x
29.
Найдем радиус-вектор точки М в системе К:r r r
r = r0 + r ¢
r r
r
r = v0t + r ¢
Радиус-вектор и координаты точки М в
обеих СО разные.
30.
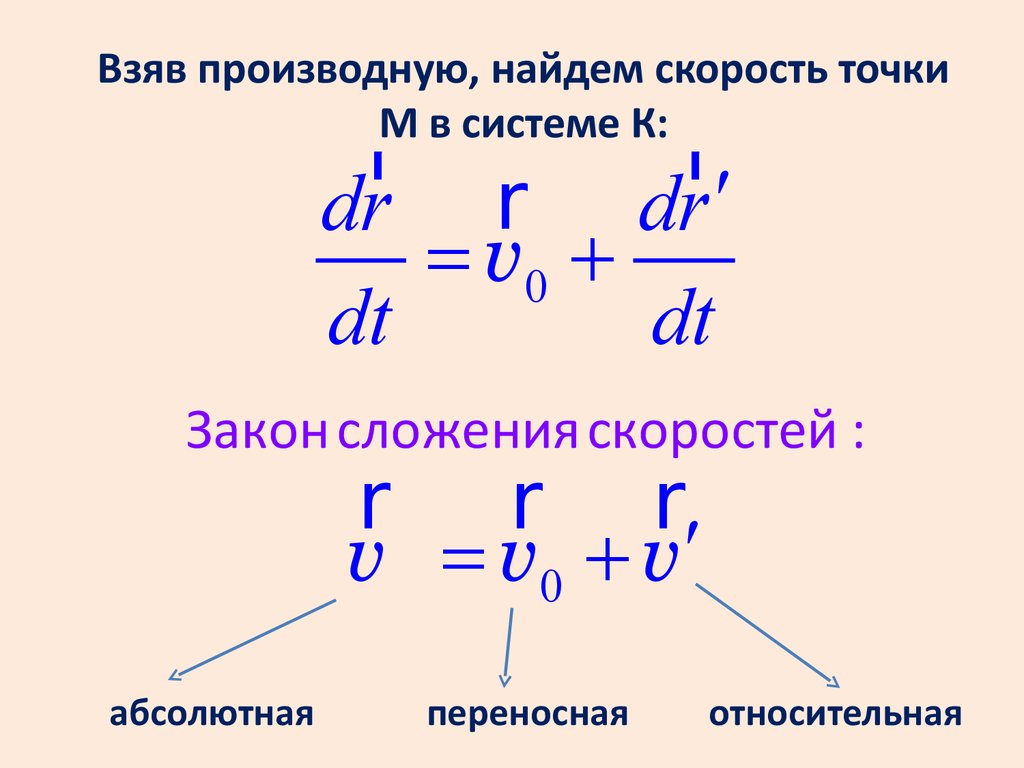
Взяв производную, найдем скорость точкиМ в системе К:
r
r
dr r dr ¢
= v0 +
dt
dt
Закон сложения скоростей :
r r r
v = v0 + v¢
абсолютная
переносная
относительная
31.
Дифференцируя скорость повремени,
найдем ускорение точки М:
r
r
r
dv dv0 dv¢
=
+
dt
dt
dt
r r
a = a¢
Ускорение точки М одинаково во всех
инерциальных системах отсчёта.
32.
Принцип относительности Галилея:в инерциальных системах отсчета
все механические явления
протекают одинаково.
33.
Если СО движется равномерно ипрямолинейно относительно другой
инерциальной СО, то она также
инерциальная. Если движение
происходит с ускорением, то эта СО
неинерциальная.



























 physics
physics








