Similar presentations:
Динамика материальной точки
1.
ЛЕКЦИЯ №2Динамика материальной
точки
2.
План лекции.1.Первый
закон
Ньютона.
Инерциальные системы отсчета
2.Сила, масса, плотность, вес тела
3.2-ой и 3-й законы Ньютона. Импульс
4.Закон
сохранения
импульса
для
механической системы
5.Неинерциальные системы отсчета
6.Момент силы
7.Кинетическая энергия. Теорема об
изменении кинетической энергии
3. 1. Первый закон Ньютона. Инерциальные системы отсчета
4.
Динамика - раздел механики, который изучаетзаконы движения и причины вызывающие те или
иные перемещения.
В основе динамики лежат законы Ньютона.
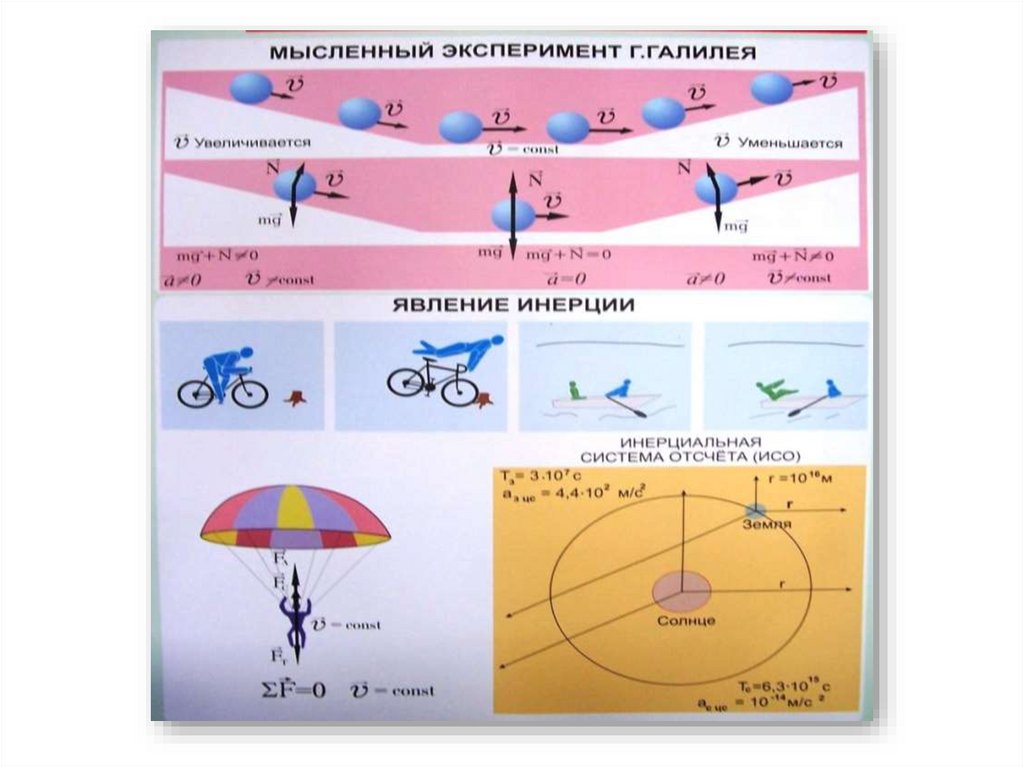
Первый закон Ньютона (закон инерции):
Всякое тело сохраняет состояние покоя или
равномерного прямолинейного движения, до тех пор,
пока внешние воздействия не выведут его из этого
состояния.
5.
Инерциальная система отсчета - системаотсчета, относительно которой свободная
материальная
точка,
не
подверженная
воздействию других тел, движется равномерно и
прямолинейно, или, как говорят, по инерции.
Инерция - это физическое явление, заключающееся
в том, что тела стремятся сохранить свою
скорость.
Инертность- это свойство тел сохранять свою
скорость.
6.
7. 2. Сила, масса, плотность, вес тела
8.
Опыт показывает, что различные тела под действиемодинаковых сил приобретают различные ускорения, т.е.
обладают различной инертностью.
Инертность тел - свойство, присущее всем телам и
заключающееся в том, что тела оказывают сопротивление
изменению их скорости (как по модулю, так и по направлению)
Масса- это мера инертности тела при поступательном
движении m- скалярная величина (кг)
Масса - величина аддитивная, это значит если тело состоит
из n количества материальных точек, тогда масса тела равна
сумме масс составляющих данное тело.
n
m mi
i 1
1
9.
В классической механикеЕсли тело движется со скоростью V1 соизмеримой со скоростью
света c = 3•108м/с, то
2
где β- безразмерный коэффициент;
m0- масса покоя тела.
10.
Плотность - распределение массы по объему.m кг
3
V м
3
Равномерное распределение m по V
4
Неравномерное распределение m по V
Сила – это физическая величина, являющаяся мерой
механического воздействия на тело со стороны других тел, в
результате которого тело приобретает ускорение или
деформируется.
кг м
F m a H 2
с
5
11.
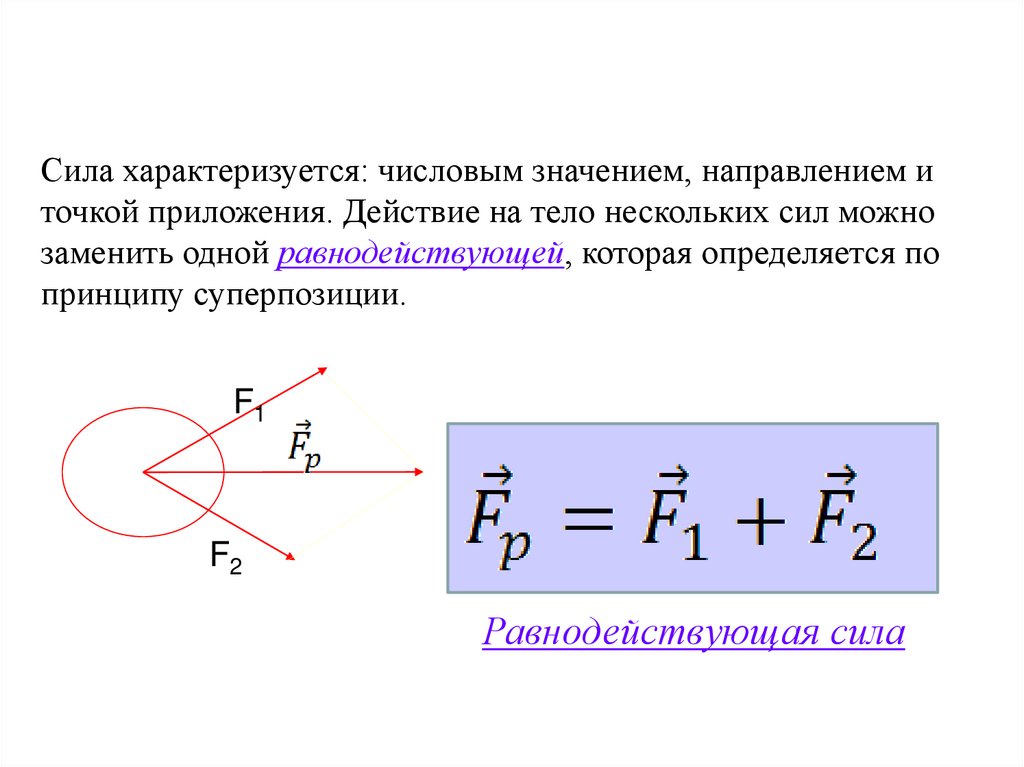
Сила характеризуется: числовым значением, направлением иточкой приложения. Действие на тело нескольких сил можно
заменить одной равнодействующей, которая определяется по
принципу суперпозиции.
F1
F2
Равнодействующая сила
12.
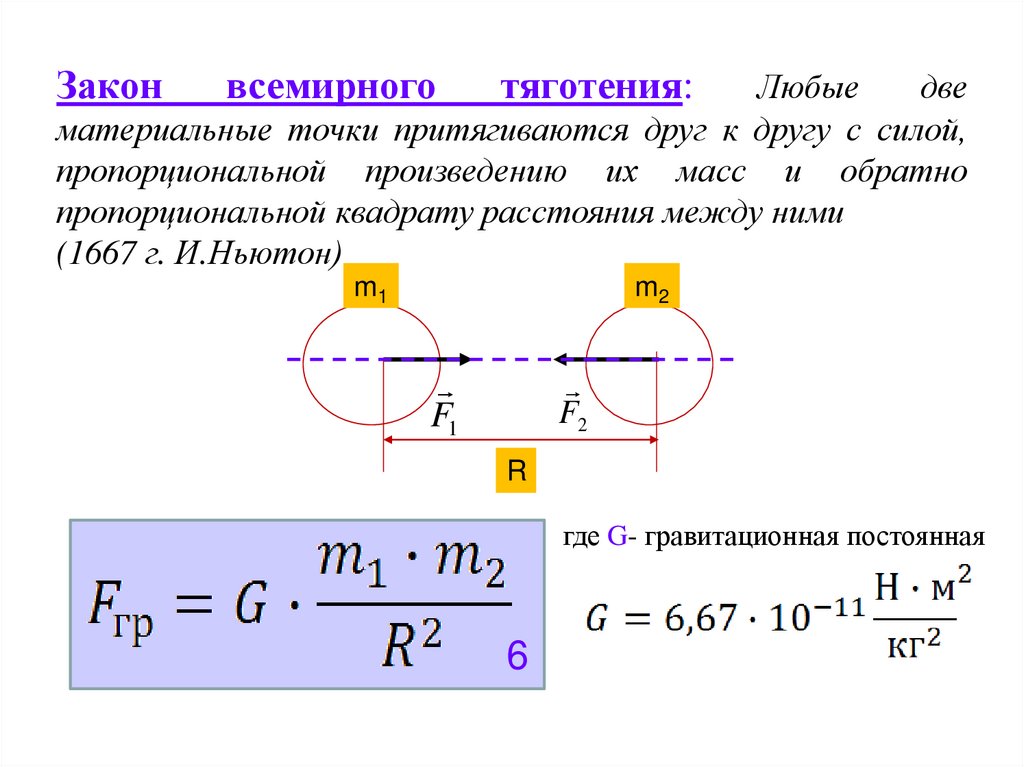
Законвсемирного
тяготения:
Любые
две
материальные точки притягиваются друг к другу с силой,
пропорциональной произведению их масс и обратно
пропорциональной квадрату расстояния между ними
(1667 г. И.Ньютон)
m1
m2
F1
F2
R
где G- гравитационная постоянная
6
13.
Эту силу называют силой тяготения илигравитационной силой. Закон всемирного тяготения
справедлив для точечных масс.
Физический смысл
Гравитационная постоянная численно равна силе, с
которой притягиваются две материальные точки
массой по 1кг на расстоянии1м.
Гравитационные силы - являются центральными,
т.е. направлены вдоль прямой, соединяющей центры
взаимодействия тел.
14.
Сила тяжести – это сила с которой тело притягивается к Земле.По закону всемирного тяготения на поверхности земли на тело
массой «m» действует сила тяжести.
M m
F G
2
R
М-масса Земли; R-радиус Земли
7
Если на тело действует только сила тяжести земли, оно
совершает свободное падение
где g –ускорение свободного падения
15.
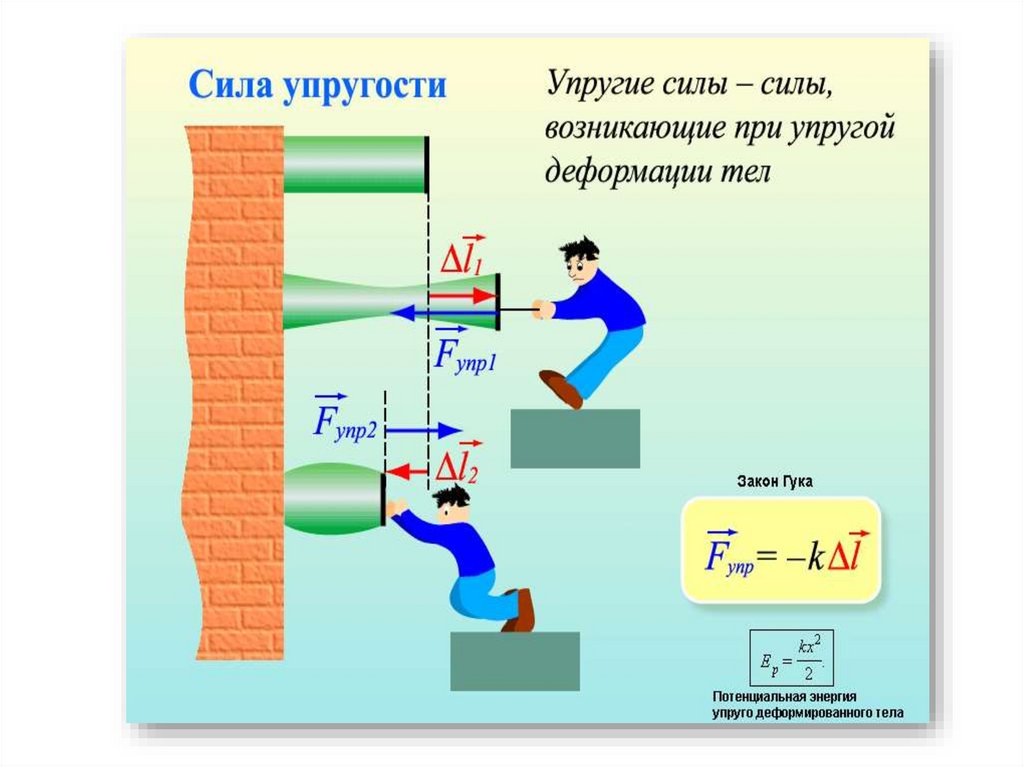
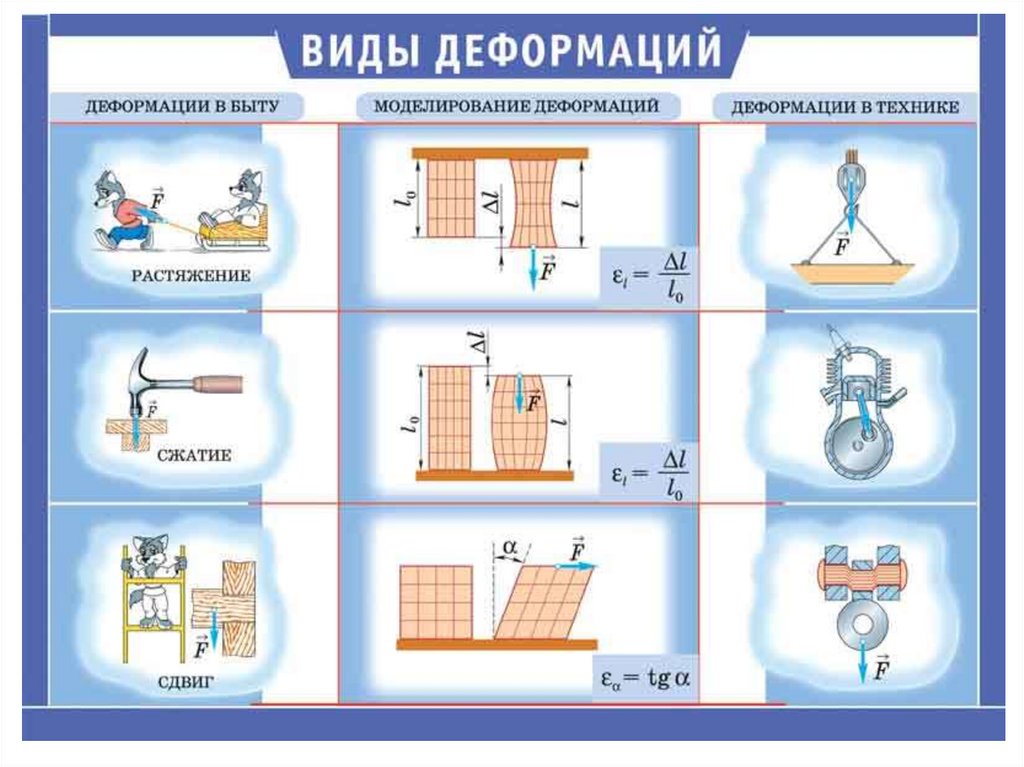
Силы упругости возникают при деформации тел•Деформация- изменение формы и объема тела при
внешнем воздействии.
•Упругая деформация –исчезает после прекращения
воздействия.
•Пластическая деформация – не исчезает после
прекращения воздействия.
•Деформация
растяжения
и
сжатия
характеризуется удлинением:
16.
17.
18.
Сила упругости - подчиняется закону Гука.Сила упругости прямо пропорциональна смещению тела
и противоположна ему по знаку.
F k x
где
8
Δx удлинение(деформация)
k- коэффициент жесткости
19.
Вес тела - это сила с которой тело действуетна опору или подвес.
Невесомость – это когда тело не действует
на опору или подвес, и вследствие этого
внутри тела отсутствует деформация
9
кг м
Н 2
с
20.
21. 3. Второй и Третий законы Ньютона. Импульс
22.
Второйзакон
Ньютона:
Ускорение
приобретаемое телом в инерциальной системе
отсчета прямо пропорционально действию на
тело силы и обратно пропорциональна его
массе.
F
а
m
10
F- равнодействующая всех сил действующих на тело.
n
F Fi
i 1
23.
Второй закон Ньютона, выраженный через импульс F= mad
a
dt
11
md
F
dt
12
Внесем массу под знак дифференциала
13
24.
Величина равная произведению массы тела на скоростьназывается импульсом
p m
Fdt - импульс силы; mV- импульс тела
14
25.
Третий Закон Ньютона утверждает, чтотела взаимодействуют с силами
равными
по
величине
и
противоположными по направлению.
Все силы всегда равны по модулю как бы они не двигались F12 = -F21
26.
При взаимодействии двух тел всегда возникает парасил, которые:
Равны по модулю
Противоположны по направлению
Лежат на одной прямой
Одной природы
Выражая силу через второй з-н Ньютона третий з-н можно
переписать:
27.
4. Закон сохраненияимпульса для
механической системы
28.
Механическая система- совокупность материальных точеки тел рассматриваемых как единое целое.
Внутренние
силысилы
взаимодействия
материальными точками системы.
между
Внешние силы- силы с которыми внешние тела действуют
на замкнутую систему.
Замкнутая система- система, которая не взаимодействует со
внешними силами.
29.
F – равнодействующая внутренних силF´ – равнодействующая внешних сил
Запишем Второй Закон Ньютона для каждой системы.
d m1 2
F 1 F1
dt
d m2 2
F 2 F2
dt
d mn n
`
Fn Fn
dt
15
30.
Сложим по численно эти уравнения и получимd m
`
`
`
F1 F1 F2 F2 Fn Fn
dt
Система замкнута, поэтому равнодействующая всех внешних сил = 0
`
`
`
Fi F1 F2 Fn 0
n
i 1
Материальная точка внутри системы взаимодействует между собой
F1= -F2, => Геометрическая сумма внутренних сил = 0, произведение от
импульса = 0
dp
0
dt
, p= const
16
31.
Закон сохранения импульса:импульс замкнутой системы
тел при любых движениях и
взаимодействиях
тел системы с течением
времени не изменяется.
32.
5. Неинерциальная системаотсчета
33.
Законы Ньютона выполняются только в инерциальныхсистемах отсчета.
Системы
отсчета,
движущиеся
относительно
инерциальной системы с ускорением, называются
неинерциальными.
В неинерциальных системах законы Ньютона, вообще
говоря, несправедливы. Однако законы динамики можно
применять и для них, если кроме сил, обусловленных
воздействие и тел друг на друга ввести силы особого рода
силы инерции.
34.
Если учесть силы инерции, то второй закон Ньютона будетсправедлив для любой системы отсчета.
17
Произведение массы тела на ускорение в рассматриваемой
системе отсчета равно сумме всех сил действующих на тело
(включая Fин )
Так как F=ma (в инерциальной системе отсчета)
ma ma Fин
18
35.
Рассмотрим конкретные примеры,действия сил инерции.
1.Силы
инерции
при
ускоренном
поступательном движении системы отсчета.
Шарик массой m движется в тележке. Если
тележку привести в поступательное движение с
ускорением α0 , то нить отклонится на α.
F Fн mg
19
36.
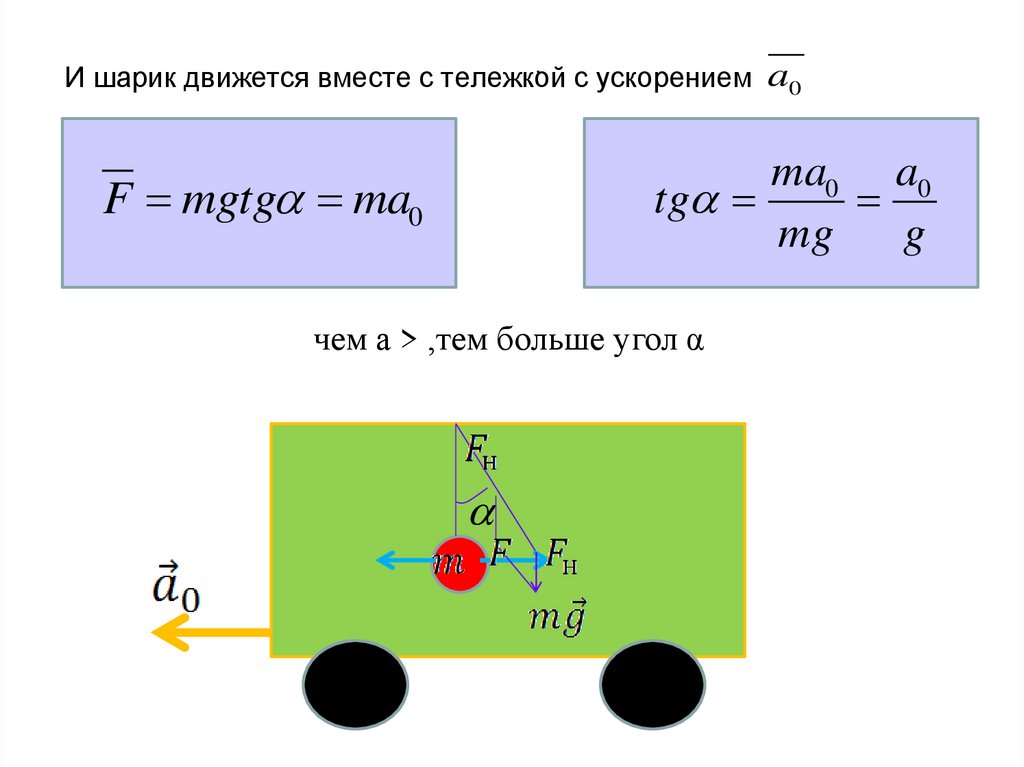
,И шарик движется вместе с тележкой
с ускорением a0
ma0 a0
tg
mg
g
F mgtg ma0
чем а > ,тем больше угол α
37.
Шарик покоится относительно систем, движущихсяс ускорением, и силе F уравновешенно силой
инерции, которая противоположно ей направления.
Fин ma0
20
38.
2. Силы инерции, действующие на тело, покоящееся вовращательной системе.
Пусть диск вращается с угловой скоростью (ω)
Fn
R
Fин
F
mg
α > если ω и R >
39.
F Fн mg21
40.
tgR
2
g
22
Шарик будет покоиться если Fин -центробежная сила инерции.
Fи н m R
2
23
Проявляются при поворотах, выполнении летчиками пилотажа, в насосах,
центрифугах.
41.
3. Силы инерции, действующие на тело, движущееся вовращательной системе отсчета.
Пусть шарик массой m движется вдоль радиуса. Если V = сonst; ω=0, то
шарик окажется в точке А; Если V= const; ω≠const, то шарик окажется в
точке В. F – сила, действующая на шарик со стороны желоба. Если V = const,
то это возможно, если F уравнено Fк - кариолисова сила инерции.
V = сonst
ω≠const
желоб
V= const
ω=0
Fи н 2m[V ]
24
42.
6. Момент силы43.
Момент силы – это скалярная величина, равнаяпроизведению модуля силы на плечо этой силы.
M F d
o
25
d
o
F
d
F
F- модули силы ;d- плечо силы- расстояние от оси
вращения до линии действия силы.
o1
44. 7. Кинетическая энергия. Теорема об изменении кинетической энергии
45.
Энергия – это скалярная физическая величина, являющаясяединой мерой различных форм движения материи и перехода
движения материи из одних форм в другие.
Кинетическая энергия
– это энергия механического
движения системы.
Пусть на покоящееся тело массой m действует сила F, создающая
перемещение dS по некоторой траектории и совершающая работу dA
dA FdS cos ,
Обозначим dS· cosα
=dS`
по второму закону Ньютона
dV
dA m
ds cos ;
dt
46.
dSТак как
= V, то
dt
dS
dA mdV
;
dt
dA mdV dV
26
47.
2mv
A
C
2
mv
A
2
2
При V=0, A=0, то и C=0 => получим
mv
Ek
2
2
27
Кинетическая энергия при поступательном движении
48.
22
2
1
mv
mv
A Ek Ek2 Ek1
2
2
28
Теорема об изменении кинетической энергии тела:
Работа сил, приложенных к телу, равна изменению
его кинетической энергии.
































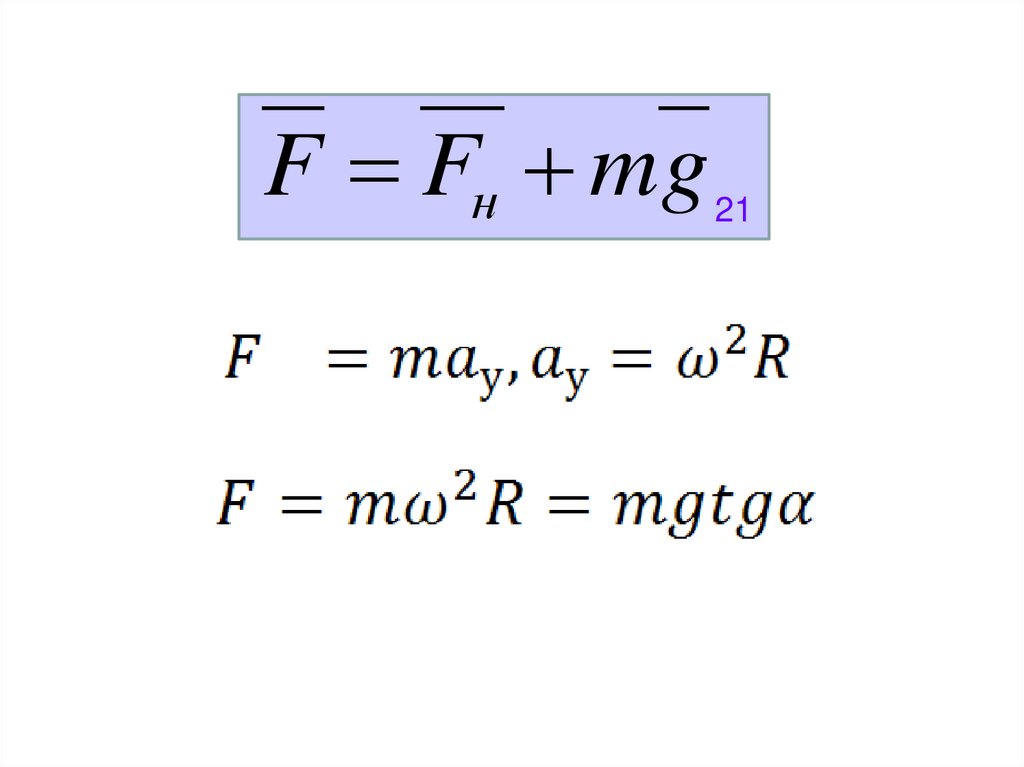









 physics
physics








