Динамика материальной точки

1. 2.2 Динамика материальной точки

Динамика - изучает движение тел, с учетом причин,
вызывающих или изменяющих это движение.
Законы динамики возникли в результате обобщения
экспериментальных фактов.
В основе динамики лежат три закона Ньютона. Эти
законы
сформулированы
материальных точек.
для
тел,
как
для

2. 2.2.1 Первый закон Ньютона

Явление сохранения скорости тела при отсутствии
действия на него других тел носит название инерция.
Первый закон динамики в формулировке Ньютона
гласит:
Тело
находится
в
состоянии
покоя
или
равномерного прямолинейного движения, если на
него
не
действуют
другие
силы
равнодействующая сил, приложенных
равна нулю.
или
к телу,

3.

С точки зрения динамики характер движения зависит
от того, каким образом выбрана система отсчета.
Система
отсчета,
в
которой
справедлив
закон
инерции, называется инерциальной системой отсчета.
Всякая система отсчета, движущаяся относительно
инерциальной
системы
прямолинейно,
отсчета
является
равномерно
также
и
инерциальной
системой отсчета.
Первый
закон
инерциальные
Ньютона
системы
вводит
отсчета
(т.е.
понятие
-
системы,
в
которых выполняется первый закон Ньютона).

4.

5. 2.2.2 Сила

Для
количественного
описания
действия
на
материальную точку других тел, вводится понятие сила.
Сила (F) - векторная величина, являющаяся мерой
механического воздействия на материальную точку
со стороны других тел, в результате которого тело
изменяет
скорость
движения
(т.е.
приобретает
ускорение) или изменяет форму и размеры.
В единицах СИ сила измеряется в Ньютонах [Н].

6.

Если к материальной точке приложено несколько
сил F1 , F2 , F3 , ....
, их действие
эквивалентно одной силе
F F1 F2 F3 ...
равнодействующей всех сил.
F1
F
F2
-

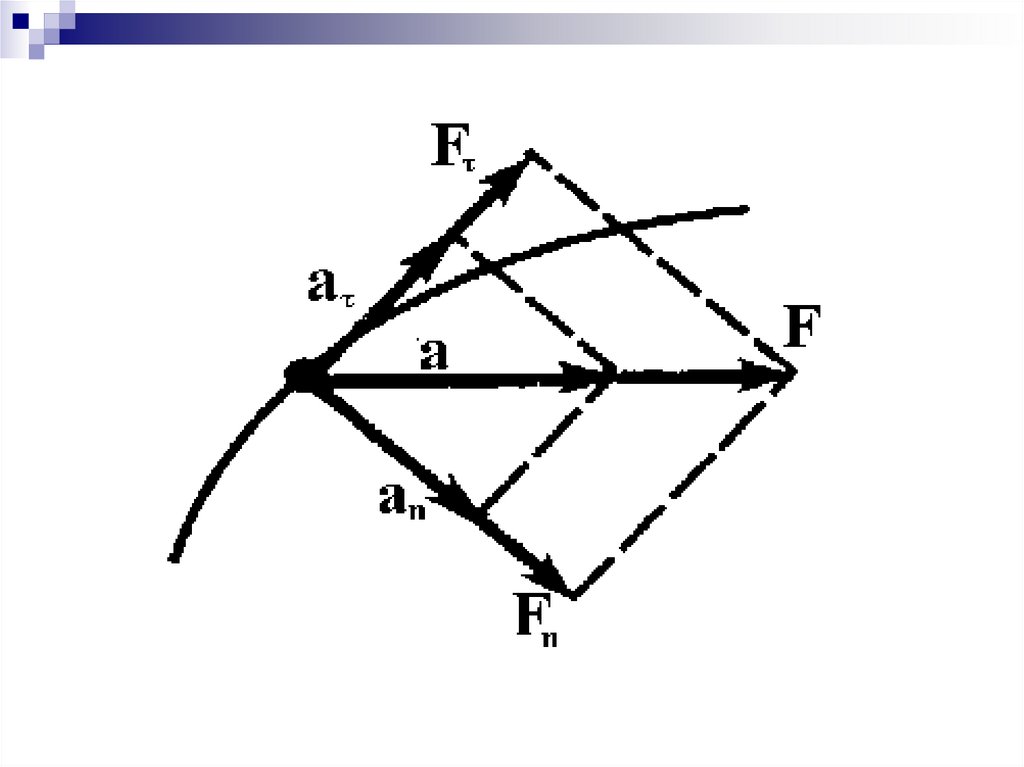
7.

Для плоской траектории вектор F направлен к центру
кривизны траектории (как и вектор a ) и он может
быть разложен на две составляющие F - касательную
к
траектории
сила) и
(касательная
или
тангенциальная
Fn нормальную к траектории (нормальная
или центростремительная сила):
F F Fn
и для центростремительной силы имеем
mv 2
Fn
R
где R - радиус кривизны траектории.

8.

9. 2.2.3 Второй закон Ньютона

Второй
закон
Ньютона
справедлив
только
в
инерциальных системах.
Ускорение, приобретаемое телом в результате
взаимодействия
с
другими
телами,
прямо
пропорционально действующей на него силе и
обратно пропорционально его массе.
F
a
m

10.

dV
F ma m
dt
где m - положительный скалярный коэффициент
пропорциональности,
постоянный
для
каждого
конкретного тела, носит название массы.
Масса
характеризует
ускоряющимся
телам,
способность
противостоять
т.е.
характеризует
масса
инертность материального тела.
Масса тела зависит от его размера и природы
вещества.
В единицах СИ масса измеряется в килограммах (кг).

11.

12. 2.2.4 Третий закон Ньютона

Две
материальные
друга
с
силами,
направленными
в
точки
действуют
равными
по
друг
на
модулю
и
противоположные
стороны
вдоль прямой, соединяющей эти точки:
F12 F21
F12 -
сила, действующая на первую материальную
точку со стороны второй;
F21 - сила, действующая на вторую точку со стороны
первой.
Силы,
подчиняющиеся
трем
законам
называются ньютоновскими силами.
Ньютона,

13.

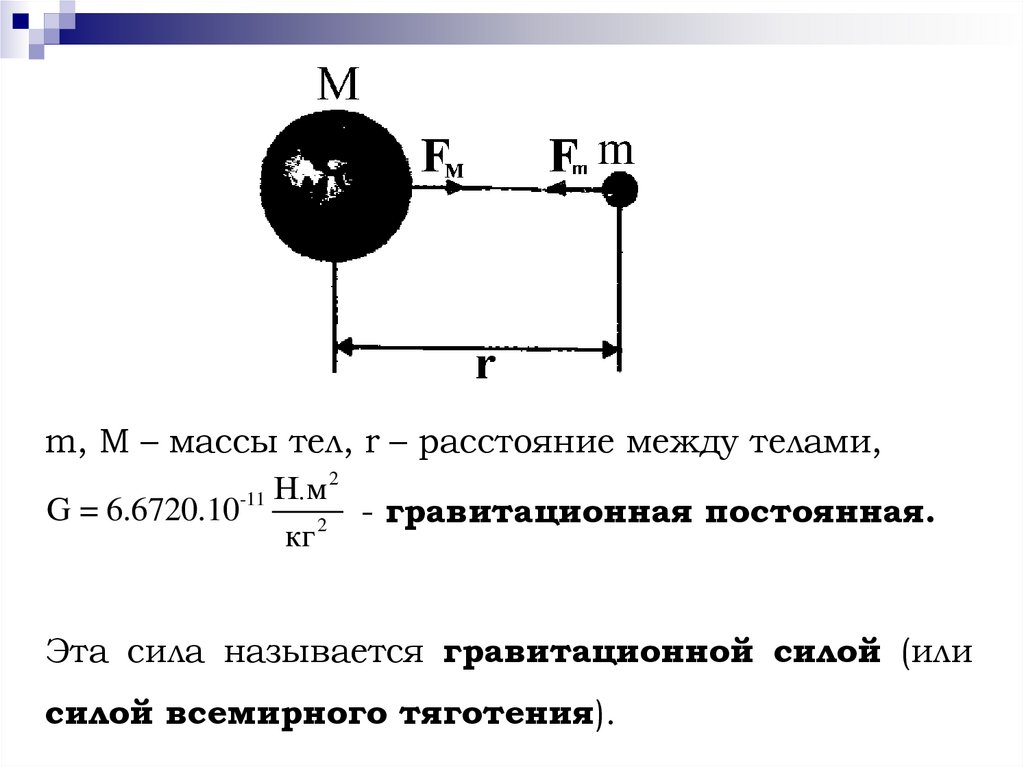
14. 2.2.5 Закон всемирного тяготения

Был сформулирован Ньютоном в 1685 г.
Между двумя материальными телами действует
сила
взаимного
притяжения
пропорциональная
произведению
тел
пропорциональная
и
обратно
прямо
массы
этих
квадрату
расстояния между ними, направленная вдоль
прямой, соединяющей эти тела.
mM
F G 2
r

15.

m, M – массы тел, r – расстояние между телами,
2
-11 Н.м
G = 6.6720.10
- гравитационная постоянная.
2
кг
Эта сила называется гравитационной силой (или
силой всемирного тяготения).

16.

Гравитационные
силы
всегда
являются
взаимодействия
между
двумя
силами
притяжения.
Сила
телами
не
зависит от среды, в которой находятся тела.
Закон всемирного тяготения установлен для тел,
принимаемых за материальные точки, т.е. для таких
тел,
размеры
которых
малы
по
сравнению
с
расстоянием между ними. Однако он справедлив и
для тел в виде шара (в этом случае r – расстояние
между
центрами
точками).
шаров,
т.е.
шары
считаются

17.

Массы, входящие в уравнение, называются
гравитационными
массами.
Этим
подчеркивается, что в принципе массы,
входящие во второй закон Ньютона
закон
всемирного
различную природу.
тяготения
и в
имеют

18.

Если сравнить второй закон Ньютона и закон
всемирного тяготения,
mM
ma G 2
r
то получим, что гравитационная сила приводит к
ускорению тела массы m на величину:
M
g G 2
r

19.

Если мы имеем дело с гравитационным притяжением
тела массы m к Земле (земная гравитация), то на
поверхности Земли
Mo
g G 2
Ro
где Мо = 5.976∙1024 кг – масса Земли,
Ro=6.371030∙106 м - радиус Земли.

20.

Подставив значения Мо и Ro в последнюю формулу,
получим
Эту
величину
м
g = 9.81 2
с
принято
называть
ускорением
свободного падения – это ускорение, приобретаемым
телом под действием гравитационной силы вблизи
поверхности небесных тел (планет, звезд).
Ускорение свободного падения одинаково для всех тел
(закон Галилея).

21.

Поскольку Земля не является идеальным шаром
(у полюсов Ro=6.356799∙106м,
на экваторе Ro=6.378164∙106м),
то величина g несколько зависит от широты
(она меняется от 9.780 до 9.832 м/с2).

22.

Сила тяжести – это сила гравитации, действующая
на тело массы m со стороны Земли.
FТ = mg.
Если тело находится на высоте h над поверхностью
Земли, то
G M0
FТ m
2
R0 h
т.е. сила тяжести с удалением от поверхности Земли
уменьшается.
Вес тела P - это сила, с которой тело вследствие
тяготения к Земле действует на опору (или подвес),
удерживающую тело от свободного падения.