Similar presentations:
Основная теорема статики
1. ОСНОВНАЯ ТЕОРЕМА СТАТИКИ
ЛЕММА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫСилу, приложенную в некоторой точке АТТ, можно переносить параллельно самой себе в любую другую точку этого тела, прикладывая при
этом пару сил с моментом, равным моменту переносимой силы относительно новой точки приложения.
Доказательство:
F2
M
d
A
F
B
F1
A
F
B
d
A
F1
( F , F1 , F2 ) ~ F в точке А т.к. ( F1 , F2 ) ~0;
( F , F1 , F2 ) ~ F1 в точке В пара сил ( F , F2 );
Следовательно, сила F в точке А эквивалентна
силе F1 в точке В и паре сил ( F , F2 ).
1
2. ОСНОВНАЯ ТЕОРЕМА СТАТИКИ
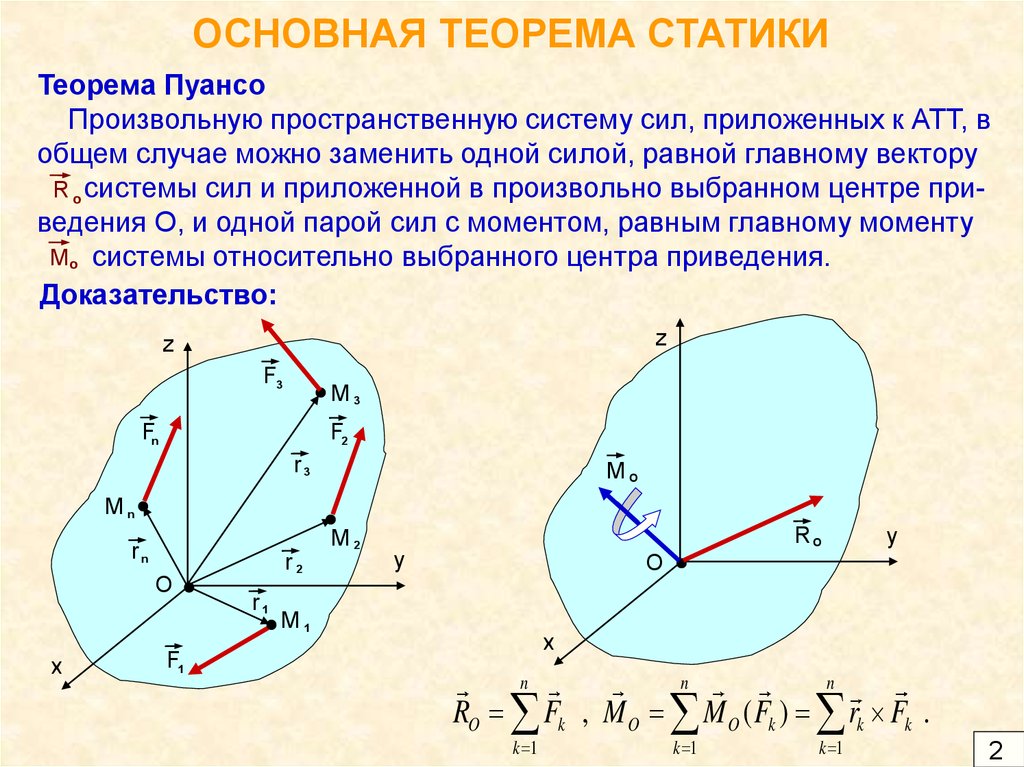
Теорема ПуансоПроизвольную пространственную систему сил, приложенных к АТТ, в
общем случае можно заменить одной силой, равной главному вектору
R о системы сил и приложенной в произвольно выбранном центре приведения О, и одной парой сил с моментом, равным главному моменту
Mо системы относительно выбранного центра приведения.
Доказательство:
z
z
F3
M3
Fn
F2
r3
MO
Mn
M2
rn
r2
O
x
F1
r1
RO
y
y
O
M1
x
n
n
n
k 1
k 1
k 1
RO Fk , M O M O ( Fk ) rk Fk .
2
3. АНАЛИТИЧЕСКИЕ ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ
nRx Fkx ,
k 1
n
Ry Fky ,
k 1
n
Rz Fkx .
k 1
n
n
M x M x ( Fk ) ( yk Fkz zk Fky ) ,
k 1
k 1
n
n
M y M y ( Fk ) ( zk Fkx xk Fkz ) ,
k 1
k 1
n
n
M x M x ( Fk ) ( xk Fky yk Fkx ) .
k 1
k 1
RO Rx2 Ry2 Rz2 ,
M O M x2 M y2 M z2 ,
cos( R x) R / R ,
O,
x
O
cos(
R
O , y ) R y / RO ,
cos( R z ) R / R .
O,
z
O
cos( M x) M / M ,
O,
x
O
cos(
M
O, y) M y / M O ,
cos( M O, z ) M z / M O .
3
4. ПЕРЕМЕНА ЦЕНТРА ПРИВЕДЕНИЯ
При перемене центра приведения главный вектор системы сил не изменяется, а главный момент системы сил относительно нового центра приведения равен главному моменту системы сил относительно старого центраприведения, сложенному с моментом главного вектора системы сил, взятого в старом центре приведения относительно нового центра приведения.
ДОКАЗАТЕЛЬСТВО
Fk
Mk
rk
rk
O
O1
rk O1O rk
Центр O :
Центр O1 :
n
R O Fk ,
k 1
n
M r F .
k
k
O
k 1
n
R O1 Fk ,
k 1
n
M r F .
k
k
O1
k 1
n
n
n
n
k 1
k 1
k 1
k 1
M O1 rk Fk (O1O rk ) Fk O1O Fk rk Fk
n
n
k 1
k 1
O1O ( Fk ) M O ( Fk ) M O O1O RO .
Величины, не изменяющиеся при каком-либо преобразовании, называют инвариантами этого преобразования. В рассматриваемом случае существуют два
инварианта: RO RO1 invar ; RO M O RO1 M O1 invar.
RO1 RO
M O1 M O O1O RO .
4
5. ВОЗМОЖНЫЕ СЛУЧАИ ПРИВЕДЕНИЯ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ЗАДАННОМУ ЦЕНТРУ
Ось динамы1) Динамический винт (динама).
О
Динамическим винтом (динамой)
называют совокупность главного
вектора и коллинеарного ему
главного момента.
Пусть в центре приведения О
Rо
≠0,
Mо
≠0,
Rо
┴
МО
О
•O
•O
МО
правый
левый
Mо
MO
R2
M2
RO
O
d
M1
M1
R1
Ось динамы
5
6. ВОЗМОЖНЫЕ СЛУЧАИ ПРИВЕДЕНИЯ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ЗАДАННОМУ ЦЕНТРУ
2) Пусть в центре приведения ОRо
≠0,
Mо
≠0,
Rо
┴
Mо
MО
R2
RO
∟
d
O
R1
d
Равнодействующая,
не проходящая через
выбранный центр приведения.
MO
RO
6
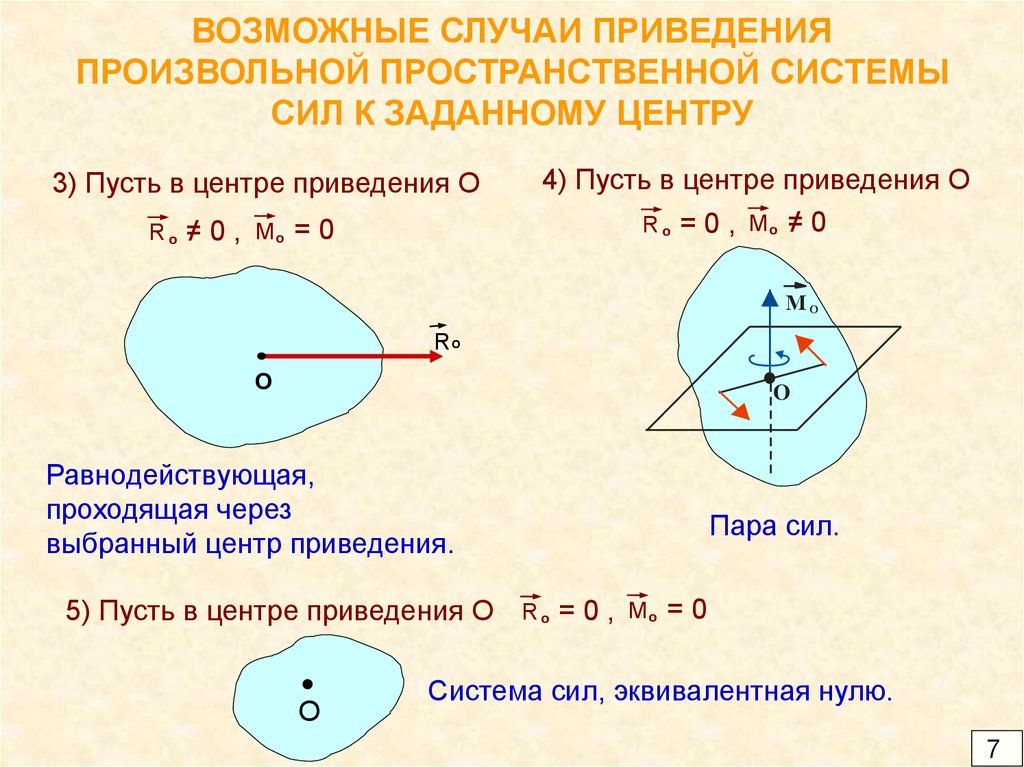
7. ВОЗМОЖНЫЕ СЛУЧАИ ПРИВЕДЕНИЯ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ЗАДАННОМУ ЦЕНТРУ
3) Пусть в центре приведения ОRо
≠0,
Mо
=0
4) Пусть в центре приведения О
R о = 0 , Mо ≠ 0
МО
RO
•O
O
Равнодействующая,
проходящая через
выбранный центр приведения.
5) Пусть в центре приведения О
О
Пара сил.
Rо
=0,
Mо
=0
Система сил, эквивалентная нулю.
7
8. ТЕОРЕМА ВАРИНЬОНА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ ДЛЯ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
Если произвольная пространственная система сил приводится кравнодействующей, то момент этой равнодействующей относительно
любого центра равен векторной сумме моментов всех сил данной
системы относительно того же центра.
Доказательство:
Пусть в центре приведения O : R O 0, M O 0.
Тогда в произвольном центре О1
M O1 M O O1O RO O1O RO M O1 ( RO ) т.к. M O 0.
n
n
k 1
k 1
С другой стороны M O1 rk Fk M O1 ( Fk ).
n
Таким образом : M O1 ( RO ) M O1 ( Fk ) .
k 1
Замечание. Данная теорема справедлива и для момента равнодействующей силы
относительно произвольной оси, что позволяет при решении задач существенно
упростить вычисление моментов сил относительно выбранных осей координат.
8
9. ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ
Пьер Вариньон (фр. Pierre Varignon)Кан,1654 —23.12,1722,Париж)
французский математик и механик,
член Парижской Академии наук,
профессор математики коллежа Мазарини,
профессор Коллеж де Франс.
Обучался в иезуитском коллеже
и университете в Кане, где стал магистром в 1682г.
Вариньон был другом Ньютона, Лейбница и Бернулли.
Основной вклад Вариньон совершил в статику и механику;
кроме того, труды Вариньона посвящены
анализу бесконечно малых, геометрии, гидромеханике.
Вариньон был самым первым пропагандистом
дифференциального исчисления во Франции.
В 1687 г. в своей работе «Проект новой механики…»
Вариньон дал точную формулировку закона
параллелограмма сил, развил понятие момента сил
и вывел теорему, получившую имя Вариньона.
В работе «Новая механика или статика,
проект которой был дан в 1687» (1725)
Вариньон дал систематическое изложение учения
о сложении и разложении сил,
о моментах сил и о правилах оперирования ими.
10. ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ
Луи́ Пуансо́ (фр. Louis Poinsot, 1777—1859) —Французский математик и механик,
академик Парижской Академии наук (1813);
пэр Франции (1846), сенатор (1852).
Известен своими трудами в области геометрии
и механики. Именно Пуансо впервые ввёл понятие
эллипсоида вращения.
В 1797 г. Пуансо окончил лицей Людовика Великого
и Политехническую школу в Париже.
В 1834 г. Пуансо опубликовал работу Éléments de statique
(«Элементы статики»), в которой им были применены
Геометрические методы исследования к учению о
равновесии твёрдых тел и их систем;
эта книга много раз переиздавалась,
причём автор неоднократно дополнял её своими
новыми статьями. Долгое время работа считалась
образцовым руководством для первоначального
преподавания механики.
В 1834 г. Пуансо построил теорию вращения
твердого тела вокруг неподвижной точки.








 physics
physics








