Similar presentations:
Момент силы относительно центра (точки)
1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА СТАТИКА
Лекция №22. 2.1 Момент силы относительно центра (точки)
3. Момент силы относительно центра
ZmO r F
B
mO F h
F
mO
h
O
r
A
4.
Моментом силы F относительно центра(точки) О называется вектор mO F равный векторному произведению радиуса вектора r , проведенного из центра О в точку А приложения силы, и
вектора силы F :
mO F r F
B
Z
F
mO
h
A
r
O
Вектор mO F приложен в точке О и направлен плоскости, проходящей через центр О и силу F , в ту сторону, откуда сила видна стремящейся повернуть
тело вокруг центра О против хода часовой стрелки.
Модуль mO F равен произведению модуля силы F на плечо h:
mO
= F·h,
где плечо h перпендикуляр, опущенный из центра О на линию действия
силы F .
Момент mO F характеризует вращательный эффект силы
но центра (точки) О.
F
относитель-
5. Свойства момента силы:
Момент силы относительно центра не изменяется при переносе силы вдольлинии ее действия в любую точку.
Если линия действия силы проходит через центр О (h = 0), то момент силы
относительно центра О равен нулю.
Для плоской системы сил при вычислении моментов сил относительно точки
(центра), находящейся в той же плоскости, пользуются понятием алгебраического момента силы относительно точки.
Алгебраический момент силы F относительно
точки О равен взятому с соответствующим знаком
произведению модуля силы на ее плечо:
mО( F ) = F h.
Момент считается положительным, если сила
стремится повернуть тело вокруг точки О против хода
часовой стрелки, и отрицательным по ходу часовой
стрелки:
mO ( F1 ) F1 h1 ;
mO ( F2 ) F2 h2 .
F1
h1 О
h2
F2
6.
РF
О
Р
F
7.
8. Пьер Вариньон
Пьер Вариньон (фр. Pierre Varignon, Кан, 1654 — 23 декабря, 1722,Париж) — французский математик, член Парижской Академии наук,
профессор математики коллежа Мазарини (1688), профессор Коллеж де
Франс.[1] Обучался в иезуитском коллеже и университете в Кане, где стал
магистром в 1682 году.
Вариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад
Вариньон совершил в статику и механику; кроме того, труды Вариньона
посвящены анализу бесконечно малых, геометрии, гидромеханике. За
исключением Лопиталя, Вариньон был самым первым пропагандистом
дифференциального исчисления во Франции. В 1687 году в своей работе
«Проект новой механики…» Вариньон дал точную формулировку закона
параллелограмма сил, развил понятие момента сил и вывел теорему,
получившую имя Вариньона. В работе «Новая механика или статика,
проект которой был дан в 1687» (1725) Вариньон дал систематическое
изложение учения о сложении и разложении сил, о моментах сил и о
правилах оперирования ими.[1]
9. Теорема Вариньона
При определении алгебраического момента силы относительноточки в случае, когда сложно найти плечо h, следует разложить
силу на составляющие, плечи которых найти проще, (часто параллельно осям координат), и применить теорему Вариньона:
если данная система сил имеет равнодействующую, то момент равнодействующей относительно любой точки О равен
сумме моментов составляющих сил, относительно той же
точки
mO ( R ) mO ( Fk ), где R Fk .
10. 2.2 Теория пар сил, свойства пар сил
Парой сил называется система двух равныхпо модулю, параллельных и направленных в
противоположные стороны сил ( F F ).
Плоскость, в которой лежат силы F и F , называется плоскостью пары, а кратчайшее расстояние d между линиями действия сил плечом пары.
Пара сил не может быть заменена одной эквивалентной ей силой, т.е. не имеет равнодействующей, так как R F F 0.
Пара может быть уравновешена только
другой парой сил.
Под действием пары сил тело вращается.
Вращательный эффект пары, характеризуется
моментом пары.
F
B
A
F
d
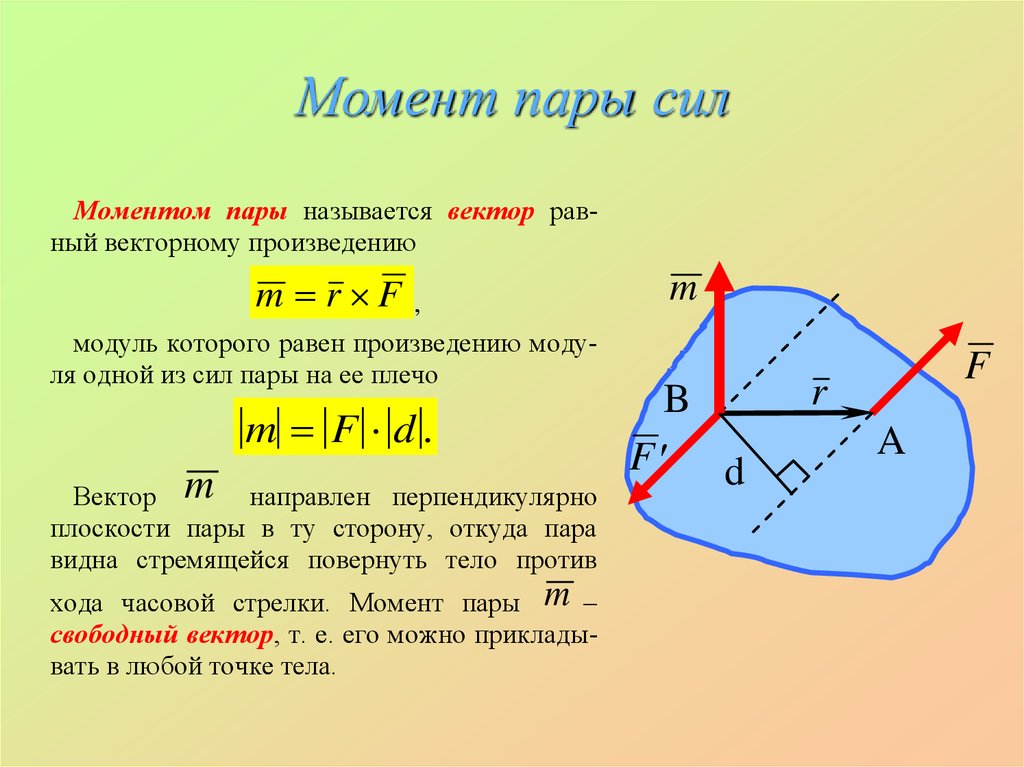
11. Момент пары сил
Моментом пары называется вектор равный векторному произведениюm r F
,
модуль которого равен произведению модуля одной из сил пары на ее плечо
m F d.
Вектор m направлен перпендикулярно
плоскости пары в ту сторону, откуда пара
видна стремящейся повернуть тело против
хода часовой стрелки. Момент пары m
свободный вектор, т. е. его можно прикладывать в любой точке тела.
m
B
F d
F
r
A
12. Свойства пар сил
1. Момент пары равен сумме моментов сил пары относительно произвольного центра (точки) О:mO mO ( F ) mO ( F ) .
2. Момент пары относительно любого центра
F
mO равен моменту пары m:
mO F h F (h d ) F d m.
mO m
h
d
B
A
F
O
3. Момент пары равен моменту одной из сил пары относительно точки
приложения другой силы пары:
m mB ( F ) mA ( F ).
13.
4. Теорема. Пары сил с равными моментами эквивалентны.Следствия:
Пару сил, приложенную к твердому телу, можно заменить другой
парой в той же плоскости, если при такой замене не изменяется величина момента пары и его направление:
Пару сил можно переносить в плоскость, параллельную плоскости
пары.
5. Теорема. Совокупность нескольких пар с моментами m1 , m2, mn
эквивалентна одной паре, момент
сумме моментов данных пар:
m которой равен геометрической
m m1 m2 mn .
6. Если на тело действует пространственная система пар, то тело находится в равновесии, если векторная сумма моментов пар равна нулю:
m 0.
14.
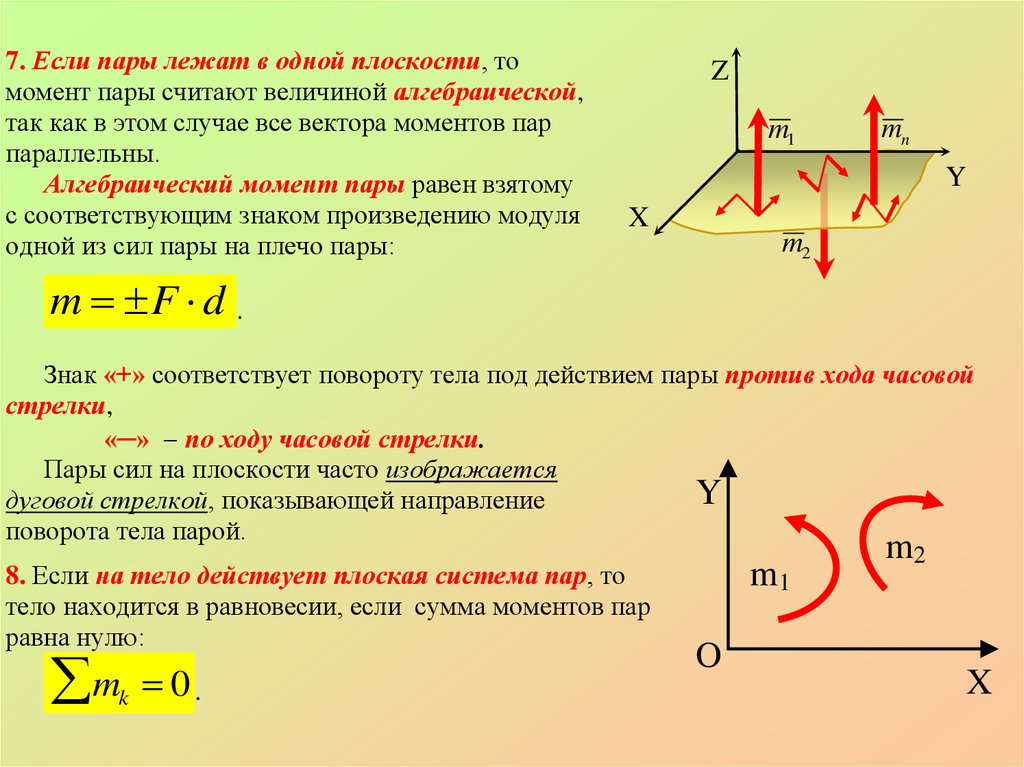
7. Если пары лежат в одной плоскости, томомент пары считают величиной алгебраической,
так как в этом случае все вектора моментов пар
параллельны.
Алгебраический момент пары равен взятому
с соответствующим знаком произведению модуля
одной из сил пары на плечо пары:
Z
m1
mn
Y
X
m2
m F d .
Знак «+» соответствует повороту тела под действием пары против хода часовой
стрелки,
«─» по ходу часовой стрелки.
Пары сил на плоскости часто изображается
Y
дуговой стрелкой, показывающей направление
поворота тела парой.
8. Если на тело действует плоская система пар, то
тело находится в равновесии, если сумма моментов пар
равна нулю:
m
k
0.
m1
O
m2
X
15.
16. 2.3 Приведение системы сил к заданному центру
Теорема Пуансо17. Пуансо Луи
Пуансо (Poinsot) Луи (3.1.1777, Париж, —5.12.1859, там же), французский математик
и механик, член Парижской АН с 1813.
Окончил
Политехническую
школу
в
Париже (1797), с 1809 профессор там же. В
период
Июльской
монархии
—
в
Министерстве народного образования. Пэр
Франции (1846), сенатор (1852). Первые
работы П. посвящены теории правильных
звездчатых
многогранников.
В
1803
опубликовал
"Элементы
статики",
в
которых применил разработанные им
геометрические методы исследования к
учению о равновесии твёрдых тел и их
систем. В 1834 построил теорию вращения
твёрдого тела вокруг неподвижной точки.
Впервые
ввёл
понятие
эллипсоида
вращения.
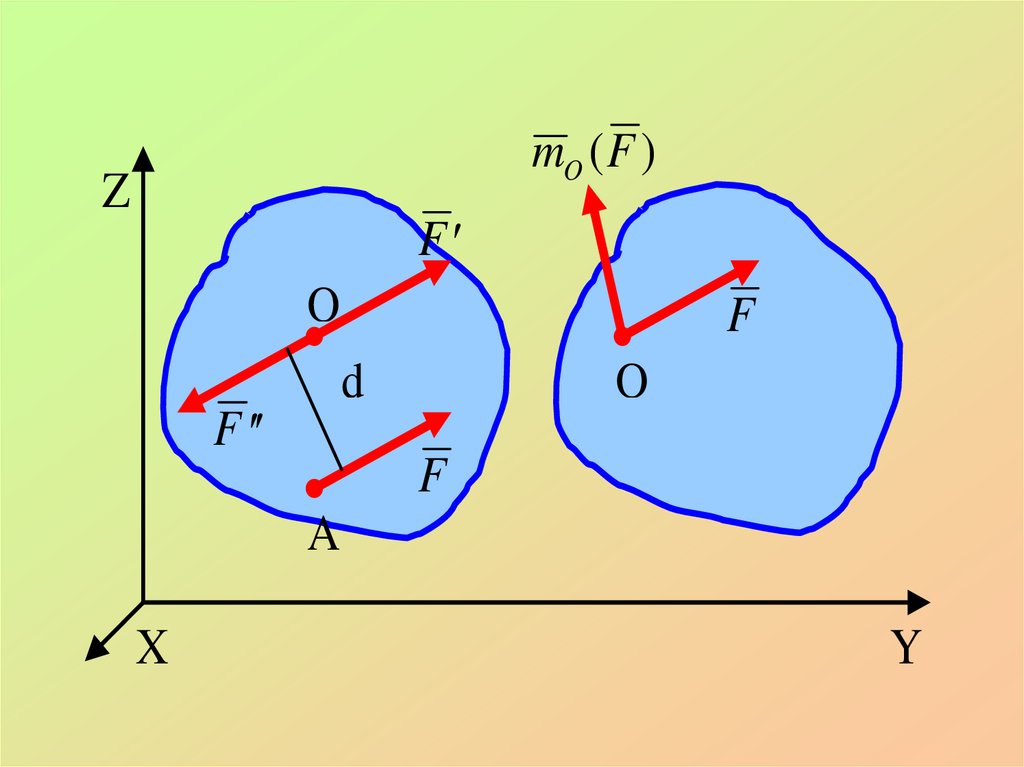
18. Теорема1 - О параллельном переносе силы (лемма Пуансо):
силу F, не изменяя ее действия наабсолютно твердое тело, можно
переносить из данной точки А в любую
другую точку О тела, прибавляя при
этом пару с моментом m равным
моменту переносимой силы
относительно точки О, в которую
переносится сила F.
19. Доказательство
mO (F )Z
F
F F F
O
F
d
F
A
X
Y
20.
mO (F )Z
F
O
F
d
F
O
F
A
X
Y
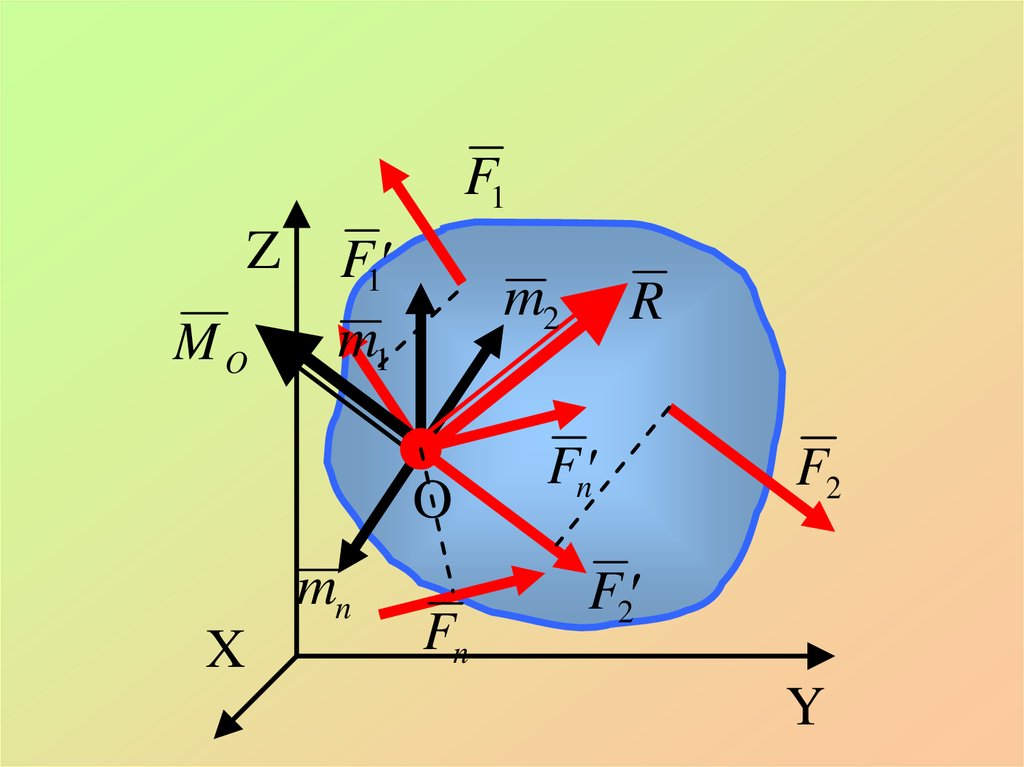
21. Теорема 2 – О приведении системы сил к заданному центру (теорема Пуансо):
Любая система сил , действующая наабсолютно твердое тело, при
приведении к произвольному центру О
заменяется главным вектором системы
сил, приложенным в центре О и парой
сил с моментом , равным главному
моменту системы сил относительно
центра О.
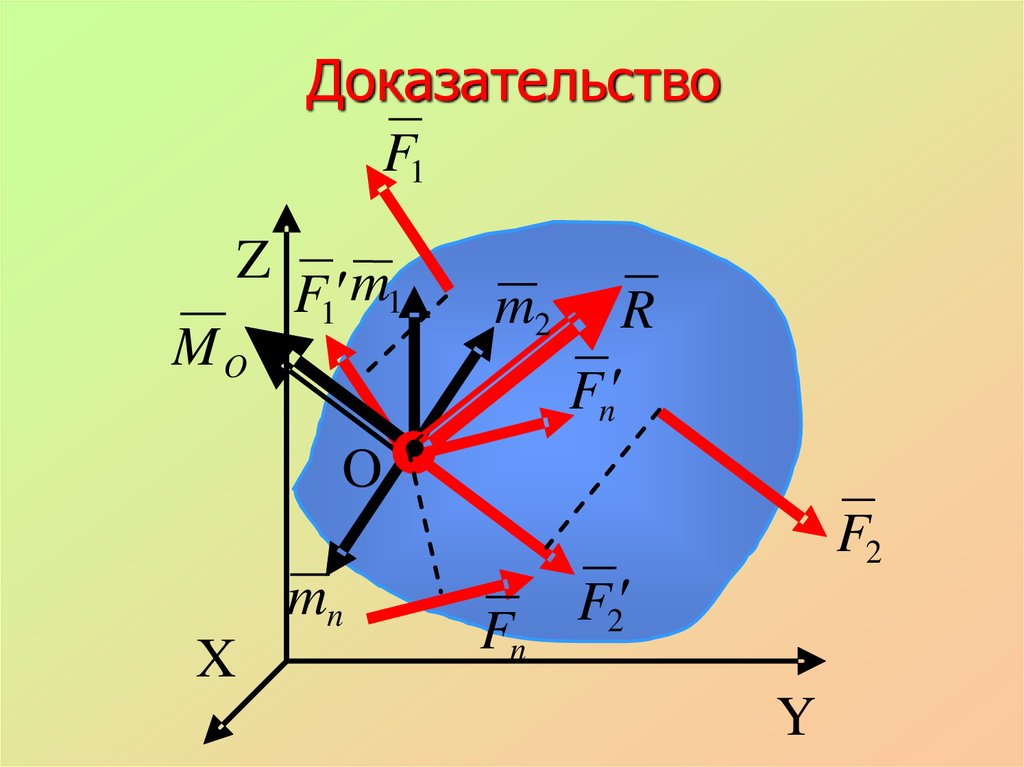
22. Доказательство
F1Z
MO
F1 m1
m2
R
Fn
O
mn
X
Fn
F2
F2
Y
23.
F1Z
MO
F1
m1
m2
O
mn
X
Fn
R
Fn
F2
F2
Y
24.
Используя теорему 1 перенесем все силы вцентр О прибавляя пары с моментами
равными моментам сил относительно
центра О. Сложив все силы и моменты
получим в центре О два вектора и равные:
k n
R F1 F2 Fn Fk ;
k 1
k n
M O M O F1 M O F2 M O Fn M O Fk .
k 1
Величина главного вектора
значение главного момента
может изменяться.
R не зависит от выбора центра О, а
M O при изменении положения центра О
25.
k nR F1 F2 Fn Fk ;
k 1
k n
M O M O F1 M O F2 M O Fn M O Fk .
Для плоской системы
сил главный вектор R
лежит в плоскости
действия сил, а главный
момент M Oперпендикулярен
этой плоскости. Поэтому
главный момент плоской
системы сил относительно
центра О определяется как
сумма алгебраических
моментов сил относительно
центра О и изображается
на плоскости дуговой
стрелкой.
k 1
Y
R XY
O
M O XY
Z
X
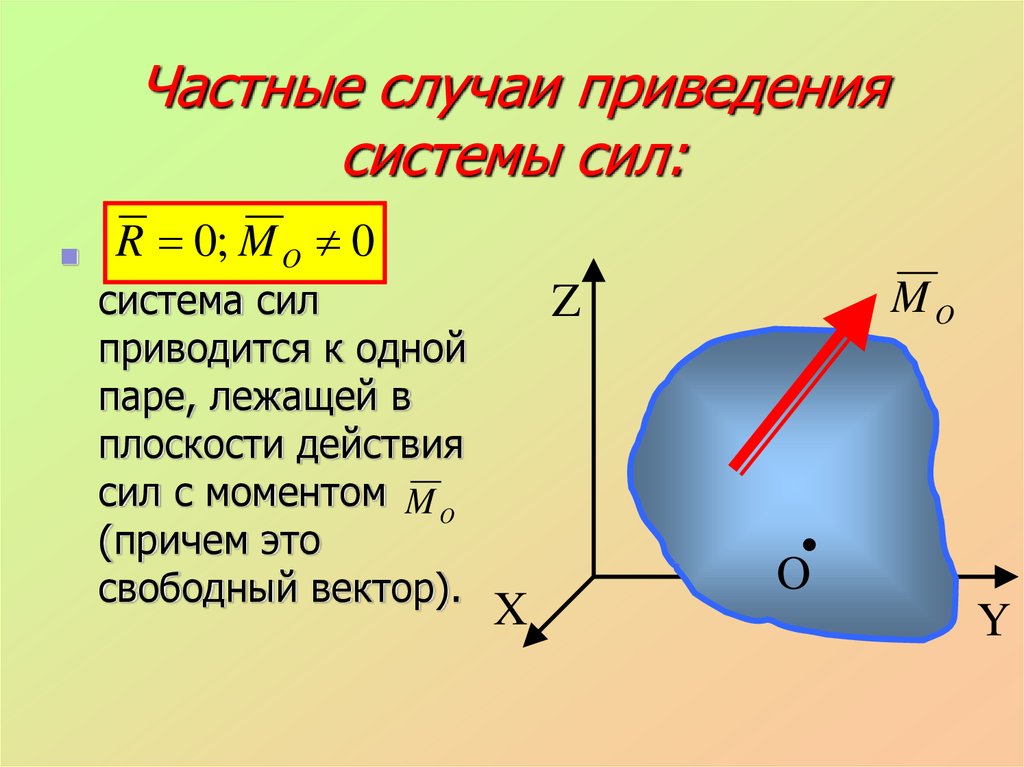
26. Частные случаи приведения системы сил:
R 0; M O 0система сил
приводится к одной
паре, лежащей в
плоскости действия
сил с моментом M O
(причем это
свободный вектор).
MO
Z
X
O
Y
27.
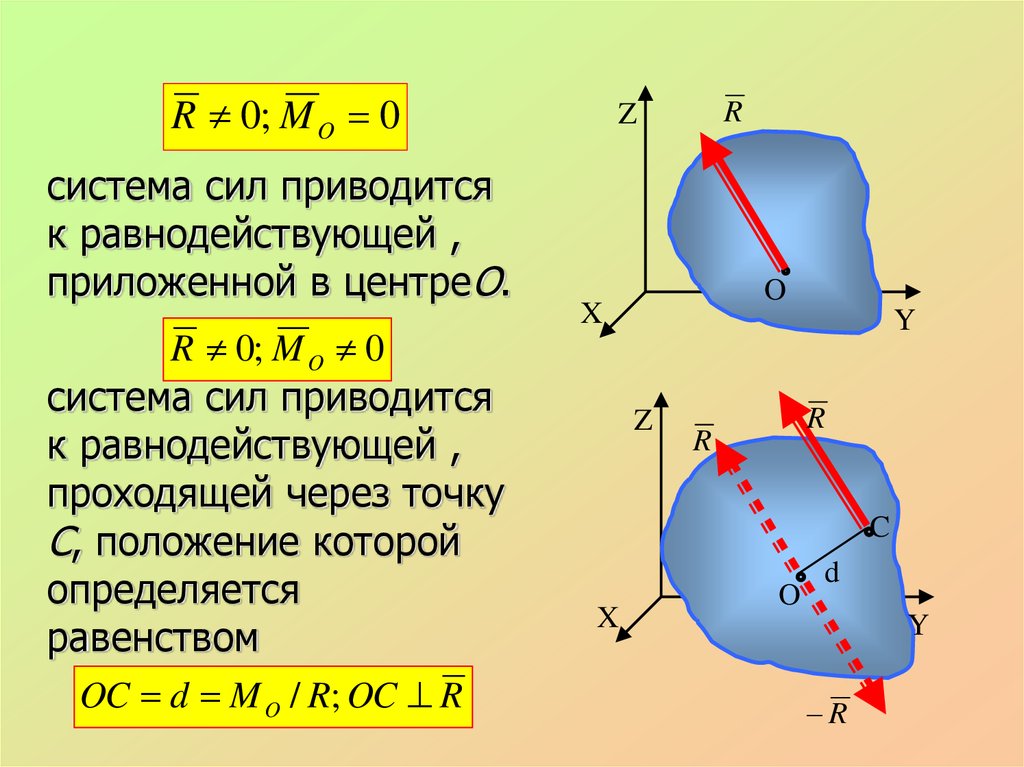
R 0; M O 0система сил приводится
к равнодействующей ,
приложенной в центреО.
R 0; M O 0
система сил приводится
к равнодействующей ,
проходящей через точку
С, положение которой
определяется
равенством
OC d M O / R; OC R
R
Z
O
X
Y
Z
R
R
C
X
O
d
Y
R
28.
R 0; M O 0система сил уравновешена.
Теорема: Для равновесия любой
системы сил необходимо и достаточно,
чтобы главный вектор и главный
момент этой системы относительно
любого центра (точки) были равны
нулю.
29. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПЛОСКОЙ СИСТЕМЫ СИЛ
Необходимые и достаточные условияравновесия твердого тела, находящегося под
действием произвольной плоской
системы сил в векторной форме имеют вид
R 0; M O O
Из этих векторных уравнений следуют три
формы аналитических условий
равновесия.
30. Основная форма условий равновесия
для сил, лежащих в плоскости ОХУ:F
kX
0; FkY 0; mO ( Fk ) 0.
Для равновесия произвольной плоской
системы сил необходимо и достаточно,
чтобы сумма проекций сил на каждую из
координатных осей и сумма моментов сил
относительно любой точки, лежащей в
плоскости действия сил, были равны нулю.
31. Вторая форма условий равновесия:
FkX
0; mA ( Fk ) 0; mB ( Fk ) 0,
OX не AB.
Для равновесия произвольной плоской
системы сил необходимо и достаточно,
чтобы суммы моментов всех сил
относительно двух точек А и В и сумма
их проекций на ось ОX,
не перпендикулярную прямой АВ,
были равны нулю.
32.
AB не OXправильно
Y
AB OX
R
Y
B
B
A
O
A
X
O
m
X
A
0; mB 0; FX 0,
но R 0, система не уравновешена!
33. Третья форма условий равновесия
m ( F ) 0; m ( F ) 0; mA
k
B
k
C
( Fk ) 0,
точки A, B, C не лежат на одной прямой.
Для равновесия произвольной плоской
системы сил необходимо и достаточно,
чтобы суммы моментов всех сил
относительно любых трех точек А, В и
С, не лежащих на одной прямой,
были равны нулю.
34.
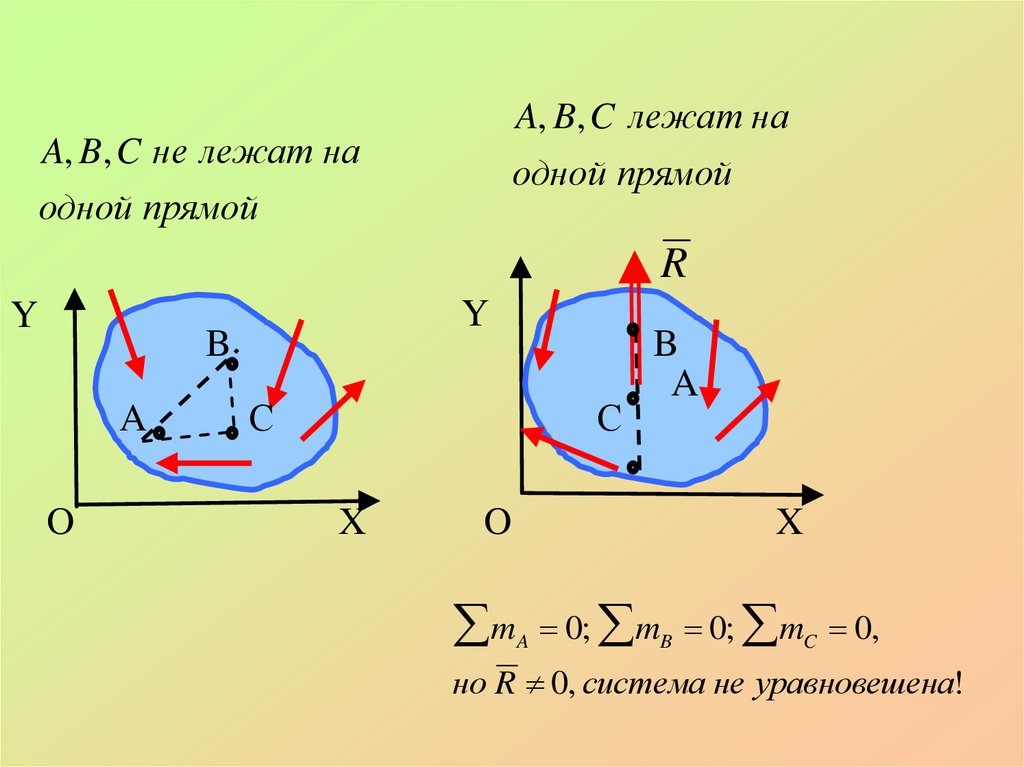
A, B, C лежат наA, B, C не лежат на
одной прямой
правильно
Y
B
A
O
одной прямой
R
Y
С
С
X
O
m
B
A
X
A
0; mB 0; mC 0,
но R 0, система не уравновешена!
35.
Для проверки решения задачина равновесие плоской системы сил
составляют сумму моментов всех сил
относительно других точек или строят в
масштабе многоугольник всех сил,
действующих на тело. Если
проверочное уравнение обращается в
тождество, а многоугольник сил
замкнут, то задача решена верно.

























 physics
physics








