Момент силы относительно центра

1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА

Моментом силы относительно центра в пространстве (векторным
моментом) называют вектор, приложенный в этой точке, с модулем,
равным произведению модуля силы на плечо относительно данной точки
и направленный перпендикулярно плоскости, содержащей линию действия
силы и моментную точку в ту сторону, откуда поворот, вызываемый силой,
кажется происходящим против движения часовой стрелки.
1) Момент силы не изменяется при переносе силы
z
МО
по линии ее действия.
•B
k
О
j
i
r
h
•А
F
2) Момент силы равен нулю если плечо силы h=0.
F h = 2 S OAB.
y
Момент силы относительно центра
можно выразить в виде векторного
произведения:
3)
Mo ( F ) =
r F r F sin F h M O ( F ) .
x
MO (F ) r F
1

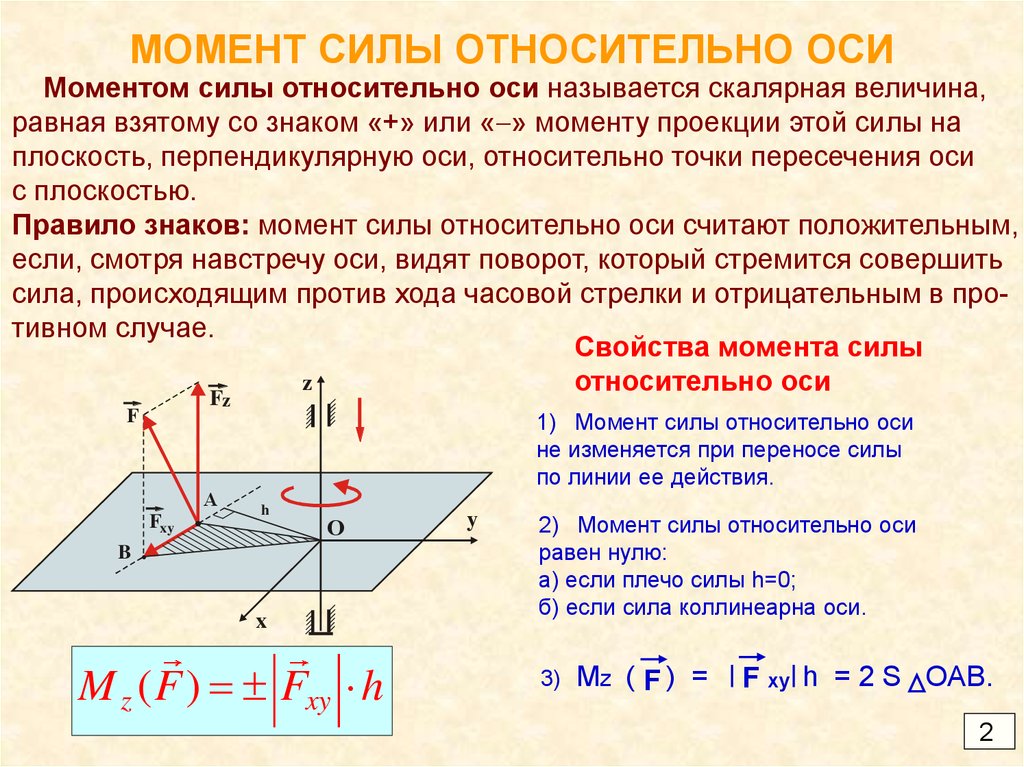
2. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ

Моментом силы относительно оси называется скалярная величина,
равная взятому со знаком «+» или « » моменту проекции этой силы на
плоскость, перпендикулярную оси, относительно точки пересечения оси
с плоскостью.
Правило знаков: момент силы относительно оси считают положительным,
если, смотря навстречу оси, видят поворот, который стремится совершить
сила, происходящим против хода часовой стрелки и отрицательным в противном случае.
Свойства момента силы
z
относительно оси
Fz
F
А
Fxy
1) Момент силы относительно оси
не изменяется при переносе силы
по линии ее действия.
h
О
B
x
M z ( F ) Fxy h
y
2) Момент силы относительно оси
равен нулю:
а) если плечо силы h=0;
б) если сила коллинеарна оси.
3)
Mz ( F ) =
F xy h = 2 S OAB.
2

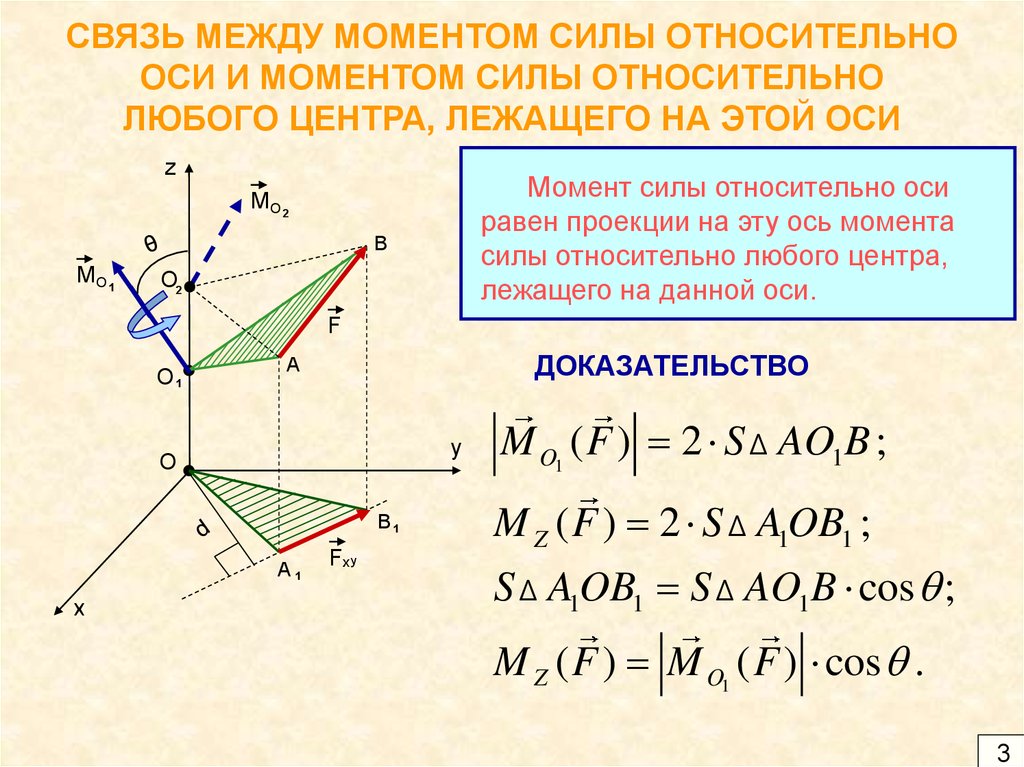
3. СВЯЗЬ МЕЖДУ МОМЕНТОМ СИЛЫ ОТНОСИТЕЛЬНО ОСИ И МОМЕНТОМ СИЛЫ ОТНОСИТЕЛЬНО ЛЮБОГО ЦЕНТРА, ЛЕЖАЩЕГО НА ЭТОЙ ОСИ

z
Момент силы относительно оси
равен проекции на эту ось момента
силы относительно любого центра,
лежащего на данной оси.
MO 2
B
MO 1
O2
F
O1
ДОКАЗАТЕЛЬСТВО
A
y
O
B1
A1
x
Fxy
M O1 ( F ) 2 S Δ AO1 B ;
M Z ( F ) 2 S Δ A1OB1 ;
S Δ A1OB1 S Δ AO1B cos ;
M Z ( F ) M O1 ( F ) cos .
3

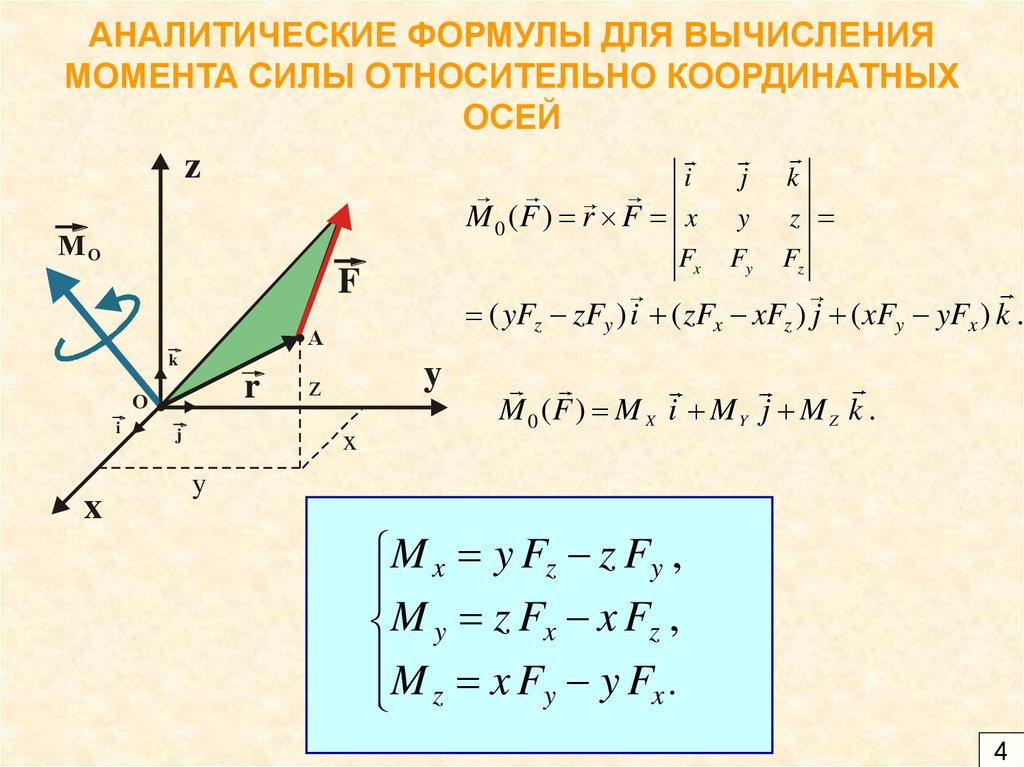
4. АНАЛИТИЧЕСКИЕ ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ МОМЕНТА СИЛЫ ОТНОСИТЕЛЬНО КООРДИНАТНЫХ ОСЕЙ

z
МО
F
О
i
x
r
j
y
z
x
j
k
M 0 (F ) r F x
y
z
Fx
Fy
Fz
( yFz zFy ) i ( zFx xFz ) j ( xFy yFx ) k .
•А
k
i
M 0 (F ) M X i M Y j M Z k .
y
M x y Fz z Fy ,
M y z Fx x Fz ,
M z x Fy y Fx .
4

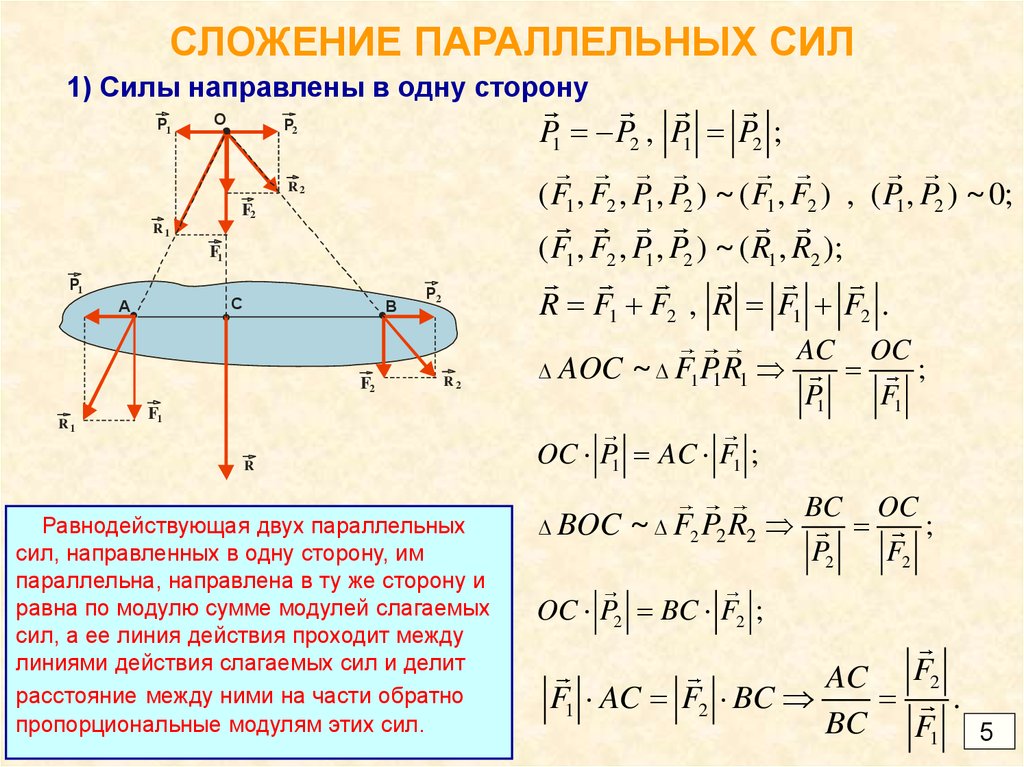
5. СЛОЖЕНИЕ ПАРАЛЛЕЛЬНЫХ СИЛ

1) Силы направлены в одну сторону
P1
O
P1 P2 , P1 P2 ;
P2
( F1 , F2 , P1 , P2 ) ~ ( F1 , F2 ) , ( P1 , P2 ) ~ 0;
R2
F2
( F1 , F2 , P1 , P2 ) ~ ( R1 , R2 );
R1
F1
P1
C
A
B
F2
R1
R F1 F2 , R F1 F2 .
P2
R2
AOC ~ F1 P1R1
F1
R
Равнодействующая двух параллельных
сил, направленных в одну сторону, им
параллельна, направлена в ту же сторону и
равна по модулю сумме модулей слагаемых
сил, а ее линия действия проходит между
линиями действия слагаемых сил и делит
расстояние между ними на части обратно
пропорциональные модулям этих сил.
AC
P1
OC
OC
F1
;
OC P1 AC F1 ;
BOC
~ F2 P2 R2
BC
P2
F2
;
OC P2 BC F2 ;
AC F2
F1 AC F2 BC
.
BC F1
5

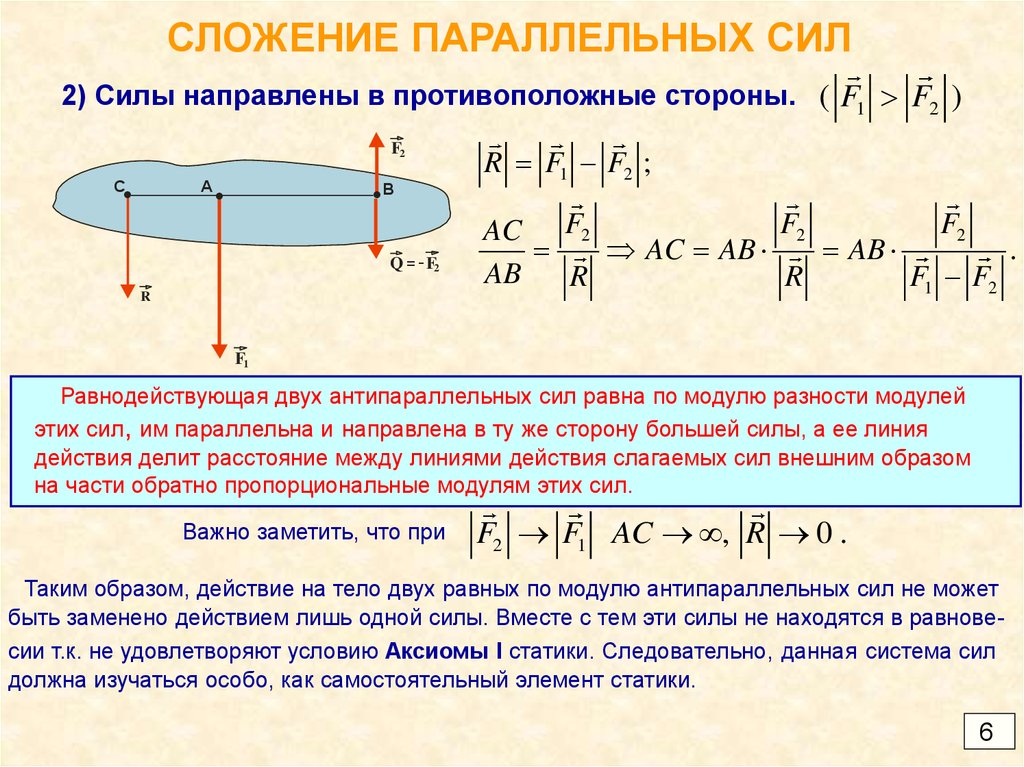
6. СЛОЖЕНИЕ ПАРАЛЛЕЛЬНЫХ СИЛ

2) Силы направлены в противоположные стороны. ( F1 F2 )
F2
C
A
•B
Q = - F2
R
R F1 F2 ;
F2
F2
AC F2
AC AB
AB
.
AB
R
R
F1 F2
F1
Равнодействующая двух антипараллельных сил равна по модулю разности модулей
этих сил, им параллельна и направлена в ту же сторону большей силы, а ее линия
действия делит расстояние между линиями действия слагаемых сил внешним образом
на части обратно пропорциональные модулям этих сил.
Важно заметить, что при
F2 F1 AC , R 0 .
Таким образом, действие на тело двух равных по модулю антипараллельных сил не может
быть заменено действием лишь одной силы. Вместе с тем эти силы не находятся в равновесии т.к. не удовлетворяют условию Аксиомы l статики. Следовательно, данная система сил
должна изучаться особо, как самостоятельный элемент статики.
6

7. ТЕОРИЯ ПАР

Парой сил называется система двух равных по модулю, параллельных
и направленных в противоположные стороны сил, действующих на АТТ.
Плоскость, проходящая через линии действия сил пары, называется
плоскостью действия пары.
Плечом пары d называется кратчайшее расстояние между линиями
действия сил пары.
Пара сил, действующая на твердое тело, может вызвать его вращение.
Вращательный эффект, создаваемый парой, зависит от:
величины момента пары, равного произведению модуля одной из сил
пары на ее плечо;
плоскости действия пары;
направления поворота, вызываемого парой в плоскости ее действия.
Все эти характеристики действия пары сил можно задать одновременно
вводя вектор-момент пары, модуль которого равен моменту пары,
направив его перпендикулярно плоскости действия пары в ту сторону
откуда поворот, вызываемый парой кажется происходящим против хода
часовой стрелки.
7

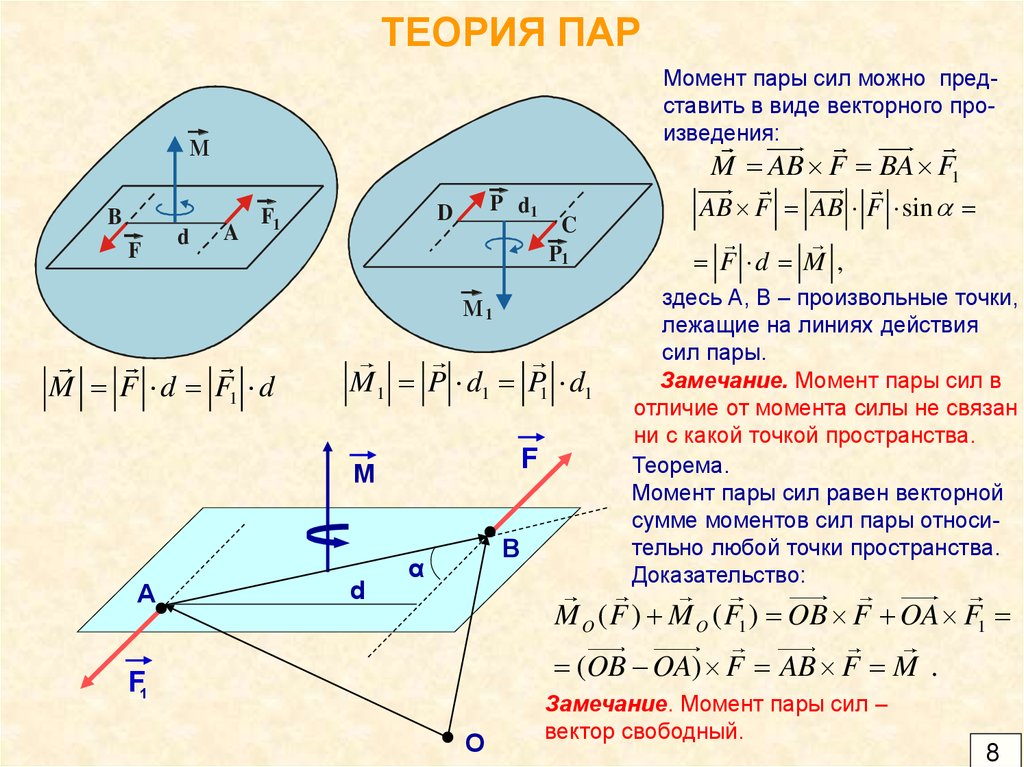
8. ТЕОРИЯ ПАР

Момент пары сил можно представить в виде векторного произведения:
М
B
F
d
A
P d1
D
F1
C
P1
М1
M F d F1 d
M 1 P d1 P1 d1
F
M
A
d
B
α
M AB F BA F1
AB F AB F sin
F d M ,
здесь А, В – произвольные точки,
лежащие на линиях действия
сил пары.
Замечание. Момент пары сил в
отличие от момента силы не связан
ни с какой точкой пространства.
Теорема.
Момент пары сил равен векторной
сумме моментов сил пары относительно любой точки пространства.
Доказательство:
M O ( F ) M O ( F1 ) OB F OA F1
(OB OA) F AB F M .
F1
O
Замечание. Момент пары сил –
вектор свободный.
8

9. ТЕОРИЯ ПАР

ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ ПАР
Теорема 1.
Не изменяя механического действия пары сил на свободное АТТ ее
можно переносить и как угодно поворачивать в плоскости действия.
Теорема 2.
Не изменяя механического действия пары сил на свободное АТТ ее
можно переносить в любую плоскость параллельную плоскости действия
пары.
Теорема 3.
Не изменяя механического действия пары сил на свободное АТТ можно
произвольным образом изменять модули сил пары и ее плечо, сохранив
неизменным их произведение (величину момента пары).
Теорема 4.
Действие системы пар сил на свободное АТТ эквивалентно действию
одной пары с моментом равным векторной сумме моментов пар системы.
M M1 M 2
n
Mn Mk .
k 1
9

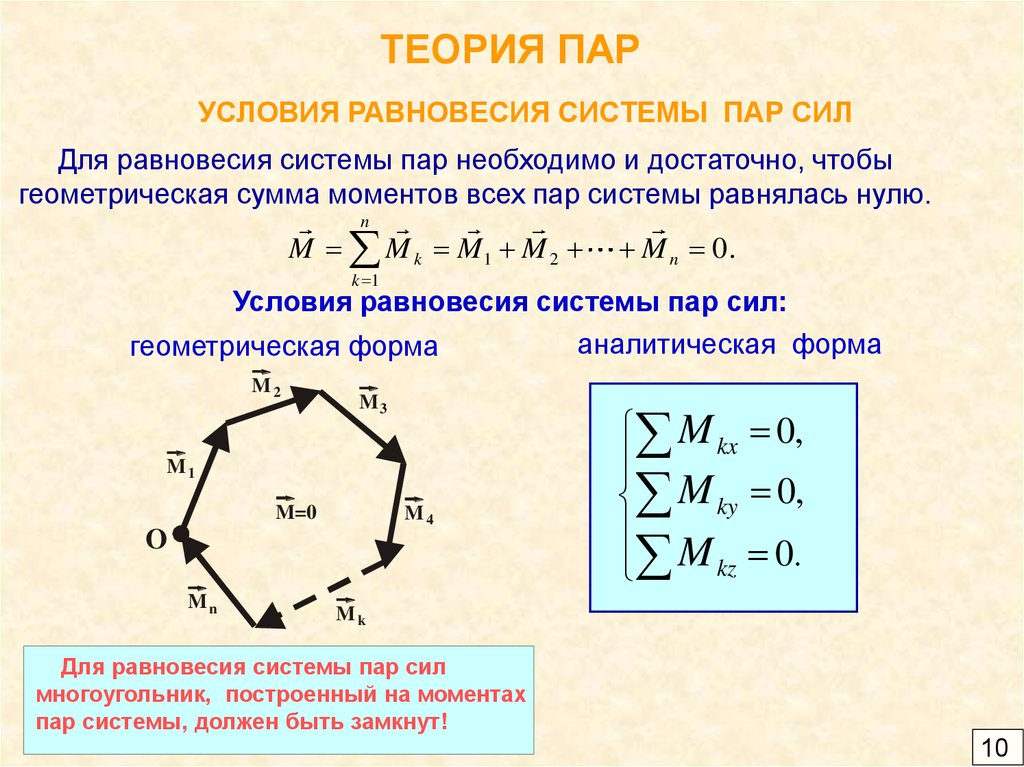
10. ТЕОРИЯ ПАР

УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ ПАР СИЛ
Для равновесия системы пар необходимо и достаточно, чтобы
геометрическая сумма моментов всех пар системы равнялась нулю.
n
M M k M1 M 2
k 1
M n 0.
Условия равновесия системы пар сил:
аналитическая форма
геометрическая форма
M2
M3
M1
M=0
M4
O
Mn
M kx 0,
M ky 0,
M kz 0.
Mk
Для равновесия системы пар сил
многоугольник, построенный на моментах
пар системы, должен быть замкнут!
10