Система сил, моменты. Геометрический метод сложения сил, приложенных в одной точке

1. Система сил, моменты

2. Геометрический метод сложения сил, приложенных в одной точке

• Поскольку силу можно переносить по
линии ее действия, то сходящиеся силы
всегда можно перенести в одну точку –
в точку пересечения этих линий
действия. Пусть даны четыре силы.
Перенесем эти силы в точку К.

3.

4.

• По правилу треугольника сложим
последовательно данные силы.
F12 F1 F2
F F123 F4
F123 F12 F3

5.

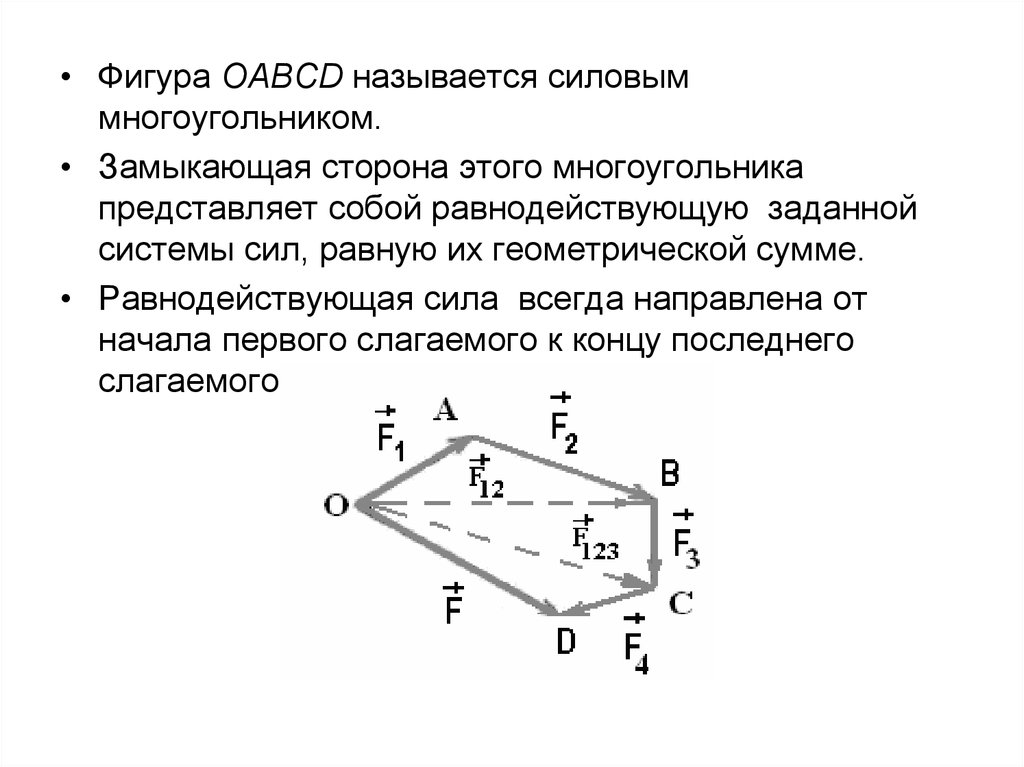
• Фигура ОАВСD называется силовым
многоугольником.
• Замыкающая сторона этого многоугольника
представляет собой равнодействующую заданной
системы сил, равную их геометрической сумме.
• Равнодействующая сила всегда направлена от
начала первого слагаемого к концу последнего
слагаемого

6. Проекция силы на ось.

• Проекция вектора на ось является скалярной величиной,
которая определяется отрезком оси, отсекаемым
перпендикулярами, опущенными на нее из начала и конца
вектора.
• Проекция вектора считается положительной, если направление
от начала проекции к ее концу совпадает с положительным
направлением оси. Проекция вектора считается
отрицательной, если направление от начала проекции к ее
концу противоположно положительному направлению оси.

7.

• Проекция силы на ось координат
равна произведению модуля силы
на косинус угла между вектором
силы и положительным
направлением оси.
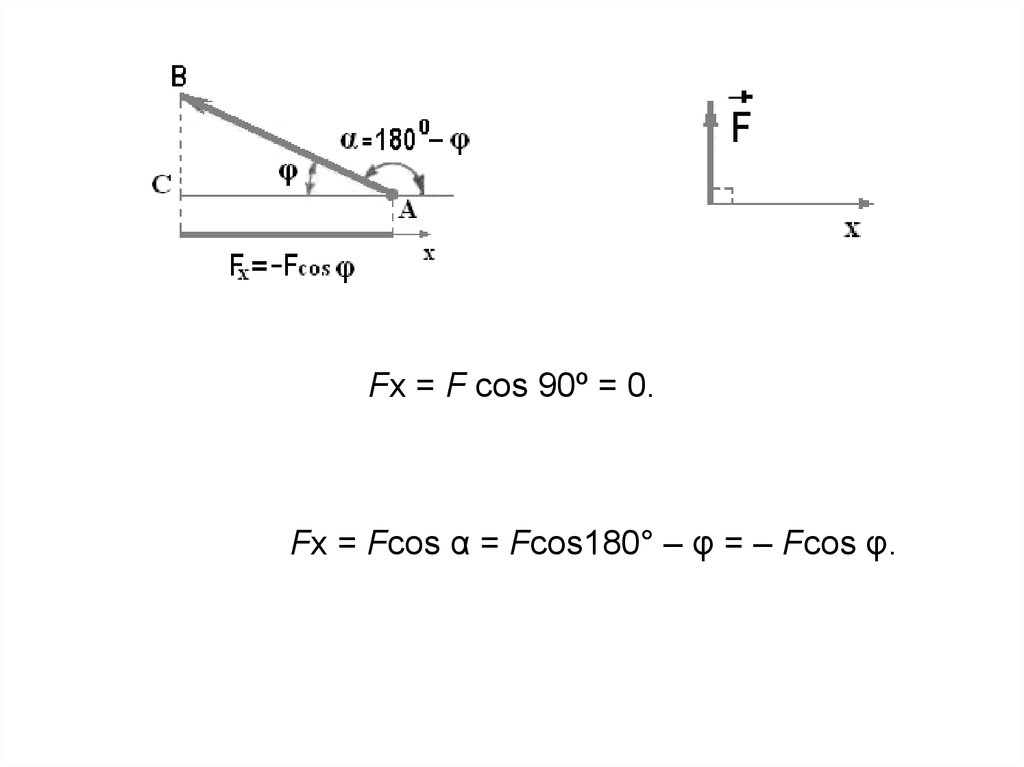
• Fx = F cos α

8.

Fx = F cos 90º = 0.
Fx = Fcos α = Fcos180° – φ = – Fcos φ.

9.

Из ΔОАВ
: Fx=F cos α, Fx=F sin φ.
F
Из ΔОАС: Fx=F cos φ, Fx=F sin α.
Модуль
силы
можно
найти
по
теореме
Пифагора
.
F F F
2
x
2
y

10.

• Проекция векторной суммы или равнодействующей
на какую-либо ось равна алгебраической сумме
проекций слагаемых векторов на ту же ось.
• Fх = F1x+F2x+F3x+ F4x

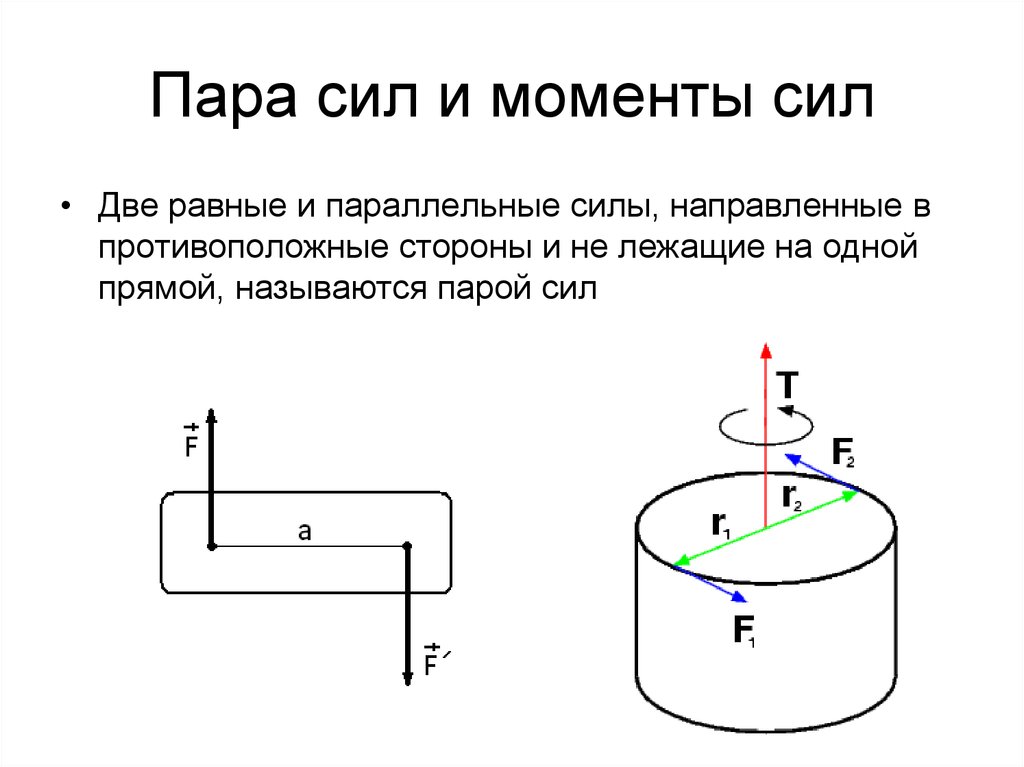
11. Пара сил и моменты сил

• Две равные и параллельные силы, направленные в
противоположные стороны и не лежащие на одной
прямой, называются парой сил

12.

• Действие пары сил на твердое тело состоит в
том, что она стремится вращать это тело.
• Способность пары сил производить
вращение определяется моментом пары,
равным произведению силы на кратчайшее
расстояние (взятое по перпендикуляру к
силам) между линиями действия сил.
• М = F·a = F '·а.
• Кратчайшее расстояние между линиями
действия сил а называется плечом пары.

13.

• Эффект действия пары сил полностью
определяется ее моментом.
• Момент пары в СИ измеряется в
ньютон-метрах (Н·м) или в единицах,
кратных ньютон-метру: кН·м, МН·м

14.

• Момент пары сил будем считать положительным, если пара
стремится повернуть тело по направлению хода часовой
стрелки, и отрицательным, если пара стремится вращать тело
против хода часовой стрелки

15.

• Две пары сил считаются эквивалентными в том
случае, если после замены одной пары другой
парой механическое состояние тела не
изменяется, т. е. не изменяется движение тела
или не нарушается его равновесие.
• Сложение пар производится алгебраическим
суммированием их моментов, т. е. момент
результирующей пары равен алгебраической сумме
моментов составляющих пар.
• М = М1 + М2 + … + Мn =
n
М
i 1
i

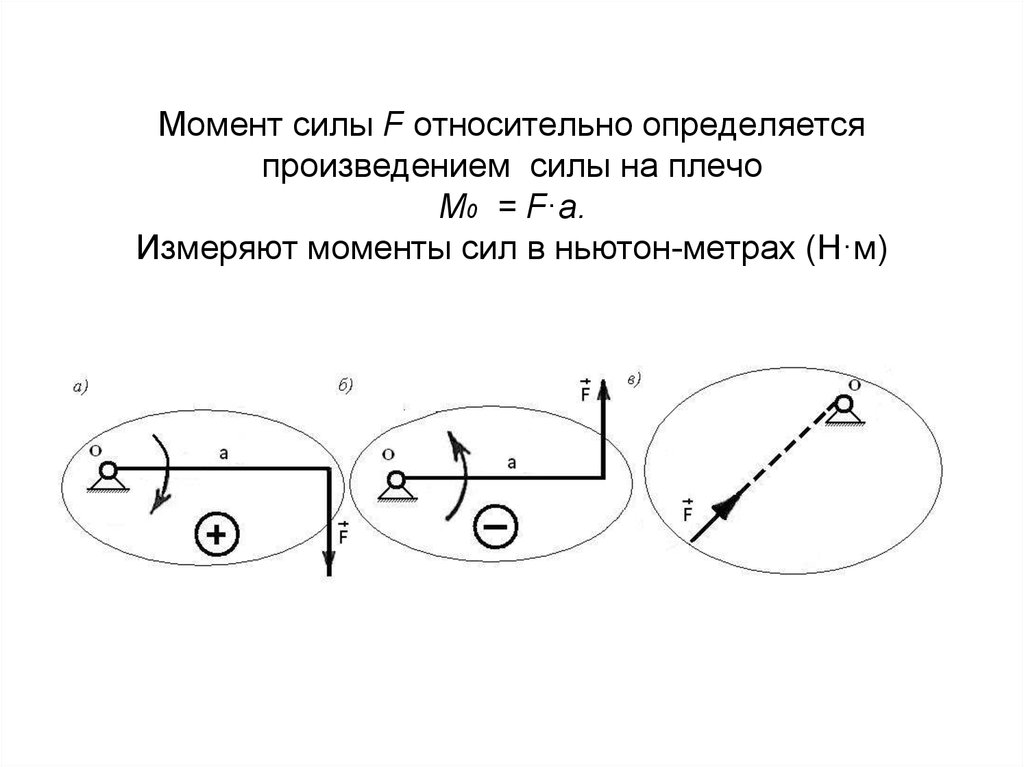
16. Момент силы относительно точки и оси

• Момент силы относительно точки определяется
произведением, модуля силы на длину перпендикуляра,
опущенного из точки на линию действия силы

17. Момент силы F относительно определяется произведением силы на плечо М0 = F·a. Измеряют моменты сил в ньютон-метрах (Н·м)

18.

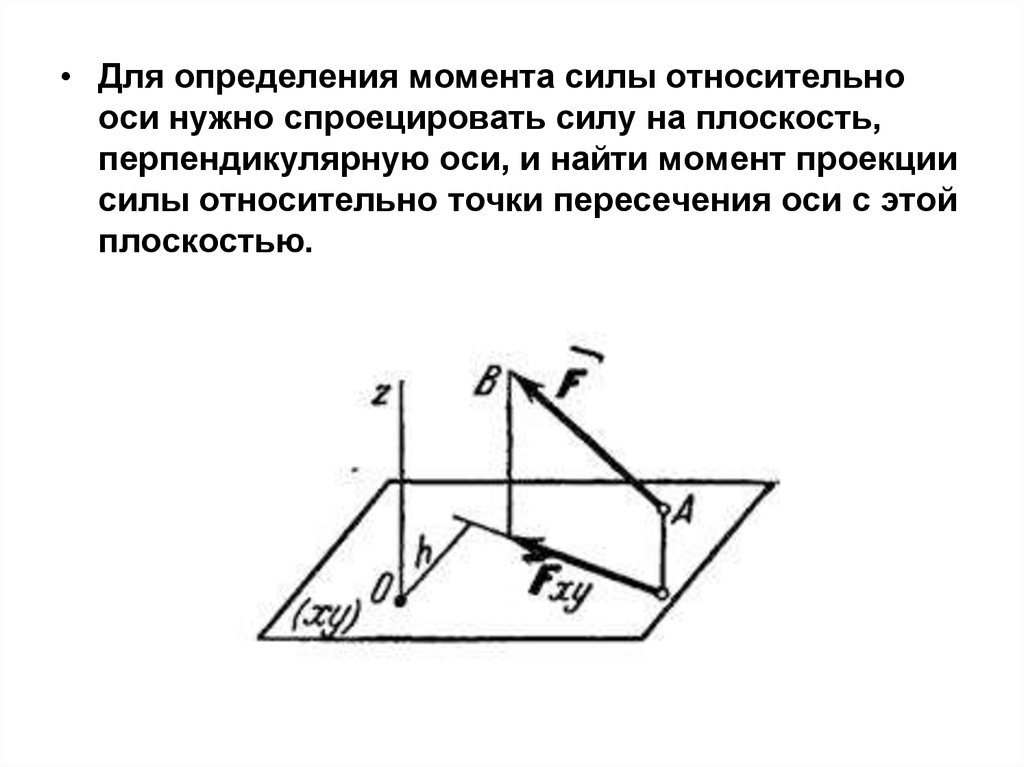
• Для определения момента силы относительно
оси нужно спроецировать силу на плоскость,
перпендикулярную оси, и найти момент проекции
силы относительно точки пересечения оси с этой
плоскостью.

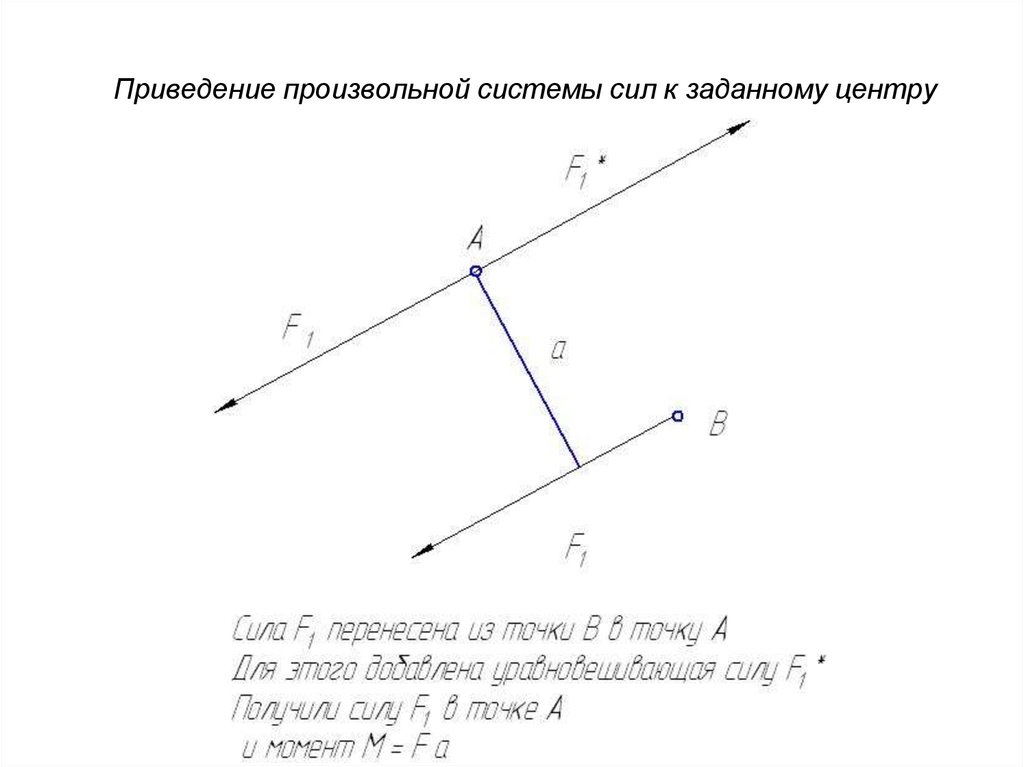
19. Приведение произвольной системы сил к заданному центру

20.

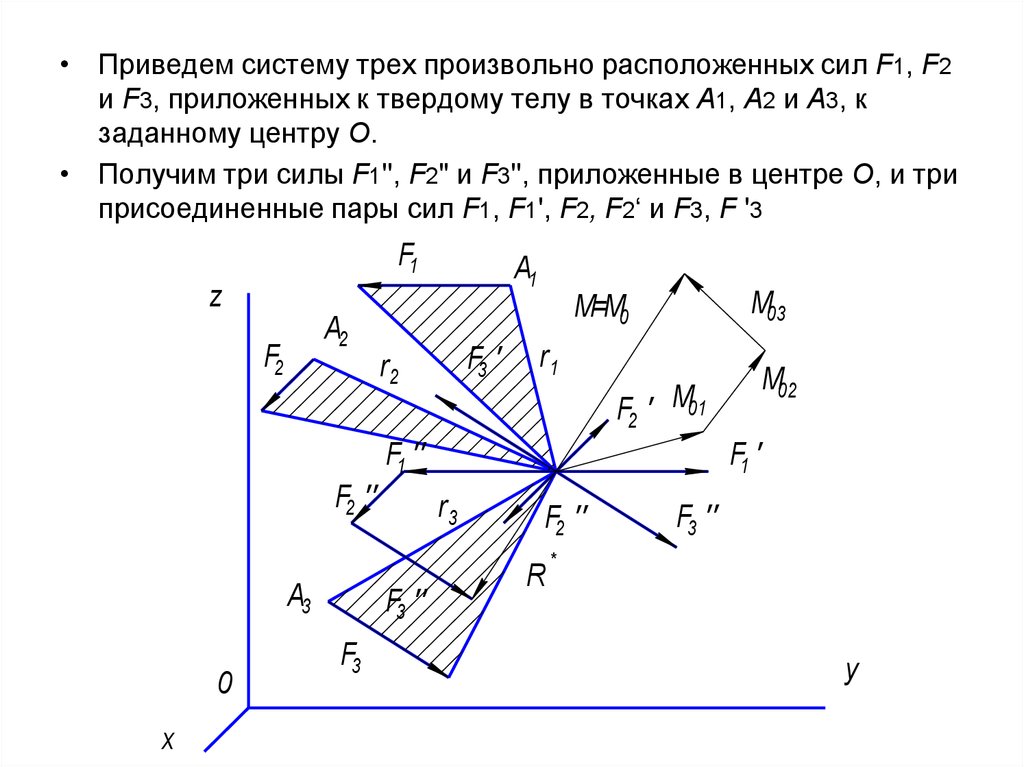
• Приведем систему трех произвольно расположенных сил F1, F2
и F3, приложенных к твердому телу в точках А1, А2 и А3, к
заданному центру О.
• Получим три силы F1'', F2" и F3'', приложенные в центре О, и три
присоединенные пары сил F1, F1', F2, F2‘ и F3, F '3
F1
A1
z
A2
F2
x
F3
r1
M02
F2 ' M01
F1 ''
F1 '
r3
F3 ''
A3
0
F3 '
r2
F2 ''
M03
M=M0
F2 ''
R
F3 ''
*
y

21.

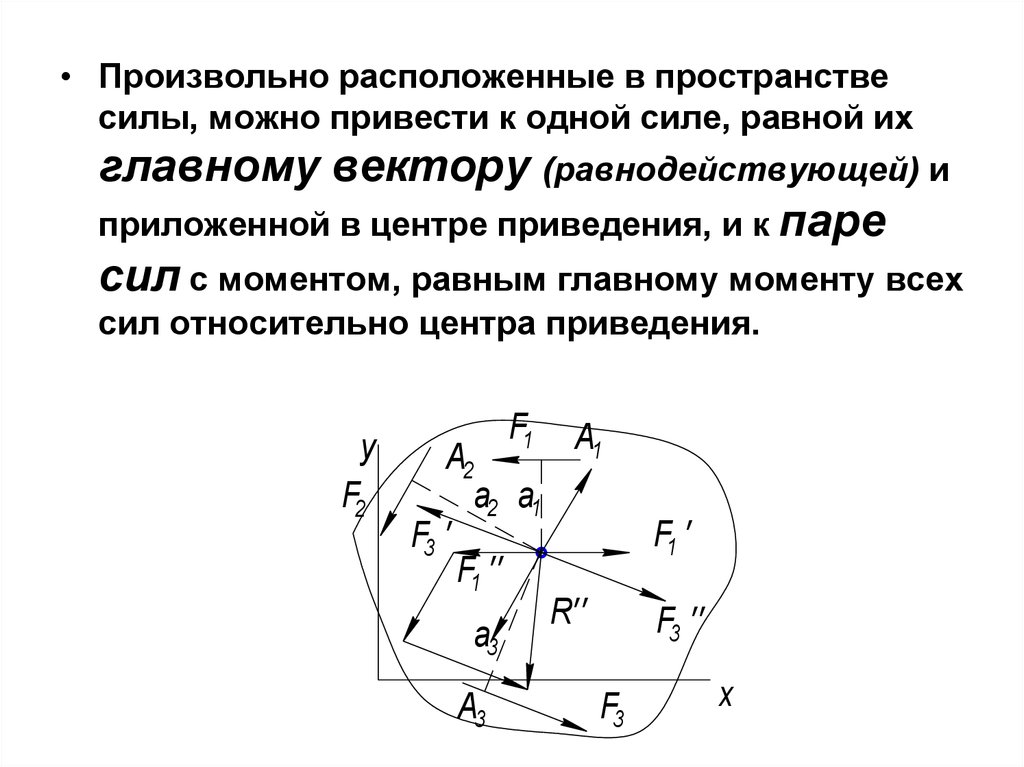
• Произвольно расположенные в пространстве
силы, можно привести к одной силе, равной их
главному вектору (равнодействующей) и
приложенной в центре приведения, и к паре
сил с моментом, равным главному моменту всех
сил относительно центра приведения.
y
F2
A2
F3 '
F1
A1
а2 а1
F1 ''
а3
A3
F1 '
R''
F3 ''
F3
x

22.

• Для вычисления главного вектора R* системы
сил, произвольно
расположенных на плоскости, воспользуемся
методом проекций.
R*=F1+F2+…+Fn.
• Обозначив Rx, Ry – проекции главного
вектора на оси координат, получим
• Rx = F1x+F2x+…+Fnx,
• Ry = F1y+F2y+…+Fny,
• где F1x, F2x, ..., Fnx; F1y, F2y, Fny – проекции
сил F1, F2, …, Fn соответственно на оси x и y.
• Модуль и направление главного вектора R*
определяются по формулам
• .
*
2
2
*
*
*
R F X Fy ; cos(R , i ) Rx / R ; cos(R , j ) Ry / R *

23.

• Все присоединенные пары сил лежат в
одной плоскости.
• Момент эквивалентной им пары сил,
равный главному моменту системы сил
относительно центра приведения,
определяется согласно как
алгебраическая сумма моментов
сил относительно этого центра.
• М = М0 =.
М
10