Сложение и разложение сил. Равновесие сходящейся системы сил

1.

СТАТИКА
Тема 5. Сложение и разложение сил.
Тема 6. Равновесие сходящейся системы сил

2. Тема 5. Сложение и разложение сил.

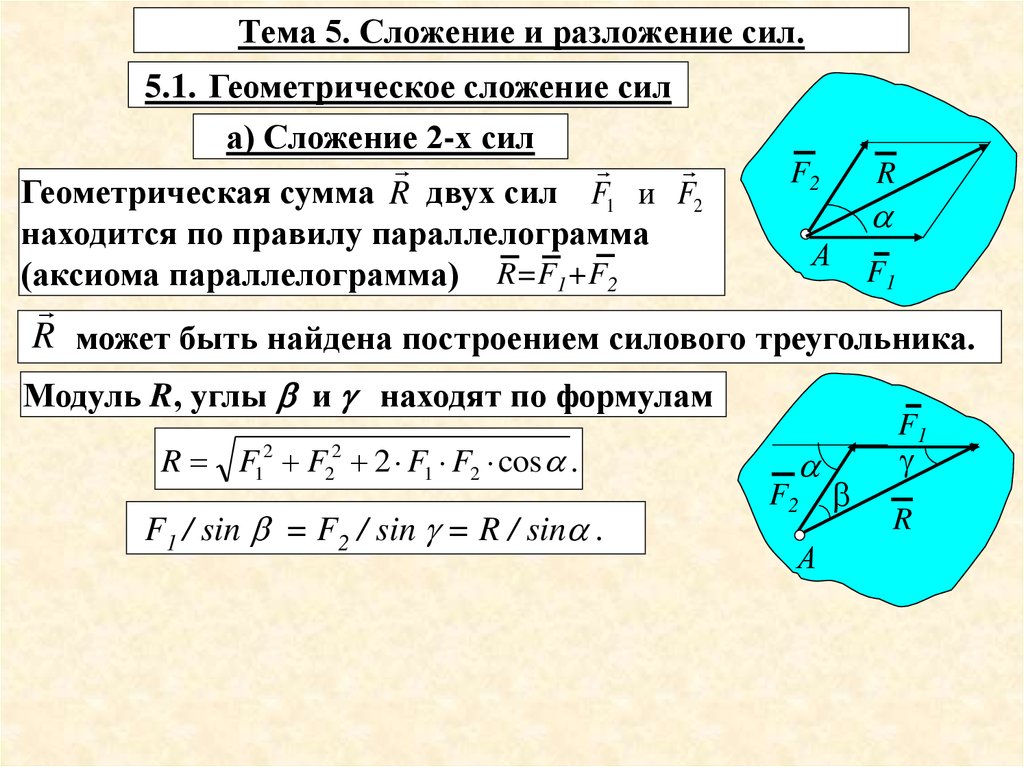
5.1. Геометрическое сложение сил
а) Сложение 2-х сил
Геометрическая сумма R двух сил F1 и F2
находится по правилу параллелограмма
(аксиома параллелограмма) R=F1+F2
F2
R
А
F1
R может быть найдена построением силового треугольника.
Модуль R, углы b и g находят по формулам
R F12 F22 2 F1 F2 cos .
F1 / sin b = F2 / sin g = R / sin .
F2
А
F1
b
g
R

3.

ЗАДАНИЕ № 15
Силы Р = 1н , Q =1н приложены в одной точке, угол между
ними = 30˚.
Равнодействующая этих сил равна (с точностью до 0,1)…
R
ВАРИАНТЫ ОТВЕТОВ:
1) 1,4 Н
2) 2,0 Н
4) 1,9 Н
3) 1,0 Н
5) 1,7 Н
Модуль равнодействующей равен длине диагонали
параллелограмма, построенного на заданных силах как на
сторонах
2
2
| R | | P | | Q | 2 | P | | Q | cos 300 12 12 2 1 1 3 / 2 1,9 Н .

4.

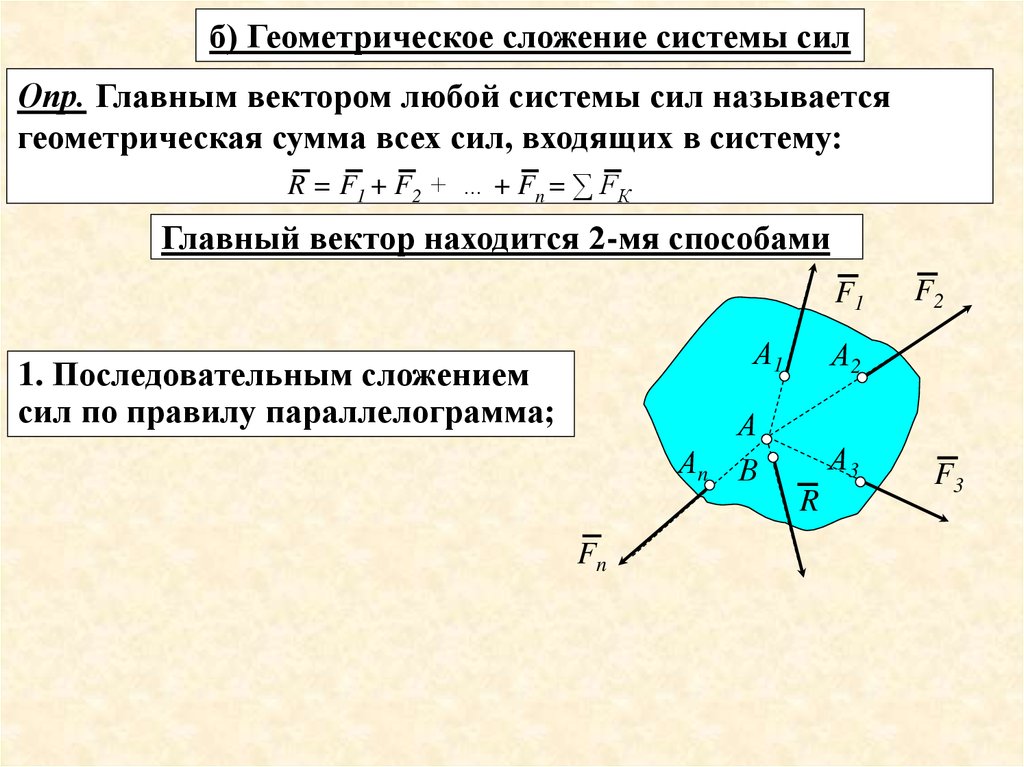
б) Геометрическое сложение системы сил
Опр. Главным вектором любой системы сил называется
геометрическая сумма всех сил, входящих в систему:
R = F1 + F2 + … + Fn = ∑ FК
Главный вектор находится 2-мя способами
F1
А1
1. Последовательным сложением
сил по правилу параллелограмма;
Аn
А2
А
В
А3
R
Fn
F2
F3

5.

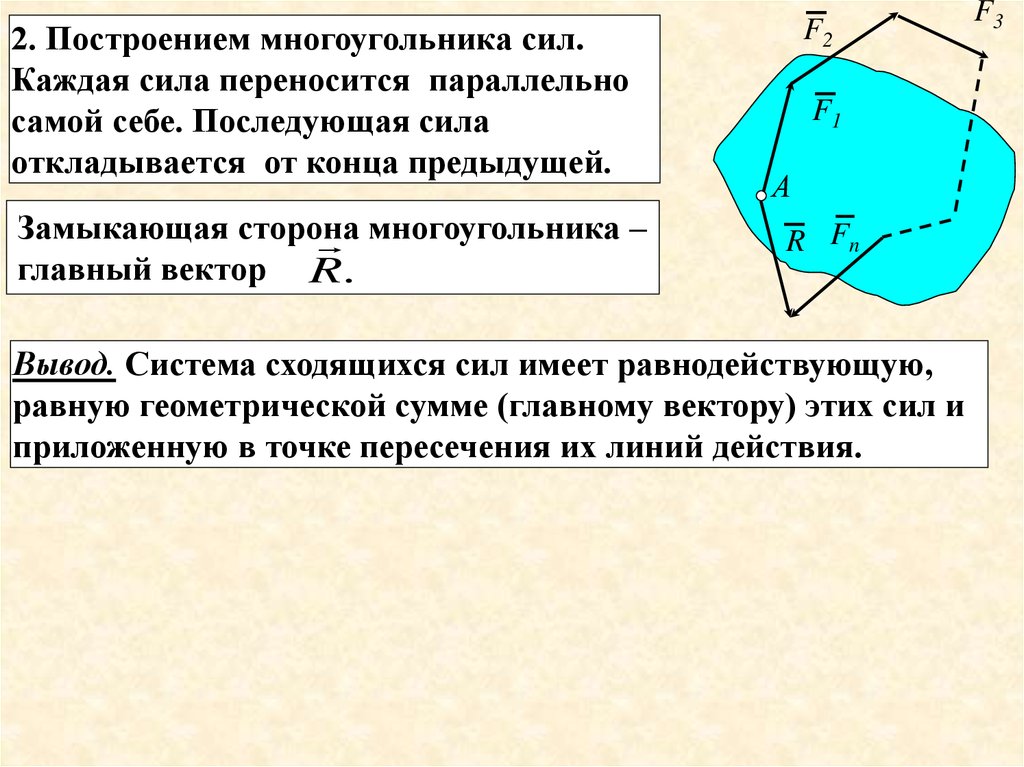
2. Построением многоугольника сил.
Каждая сила переносится параллельно
самой себе. Последующая сила
откладывается от конца предыдущей.
Замыкающая сторона
многоугольника –
главный вектор R.
F2
F1
А
R Fn
Вывод. Система сходящихся сил имеет равнодействующую,
равную геометрической сумме (главному вектору) этих сил и
приложенную в точке пересечения их линий действия.
F3

6. 5.3. Разложение силы по двум заданным направлениям

Пусть требуется разложить силу R по двум заданным
направлениям АВ и АD.
Построим параллелограмм, у
которого разлагаемая сила является
диагональю, а стороны || заданным
направлениям.
Силы F1 и F2 , направленные по
сторонам параллелограмма будут
составляющими силами.
B
F2
А
R
F1
D

7.

5.4. Аналитический способ задания и сложения сил
а) Проекция силы на ось
Опр. Проекцией
силы (или любого другого
вектора) F на ось Ох называется взятая с
соответствующим знаком скалярная
величина Fх , равная длине отрезка ,
заключенного между проекцией начала и
проекцией конца данного вектора на ось Ох.
F
А
х/
Fх
а
b х
Проекцией силы на ось равна произведению модуля силы на
косинус угла между силой и положительным
направлением оси
Fх= ab = | F | ∙ сos .
аb Fx
cos
F F
О
Fx F cos .
Если угол острый, то проекция Fх > 0 , так как сos > 0.

8.

Q
Если угол 1 тупой, то проекция Qх < 0 ,
так как сos 1 < 0 и
Qx=| Q|· сos 1=−|Q |·сosb= −dc.
1
b
А
Оd
х/
c
Если угол 900 , то проекция силы на ось ровна 0, так как
Рx = | Р | · сos 900 = 0.
Р
В
х

9.

б) Проекция силы на плоскость.
Опр. Проекция
силы F на плоскость Оху вектор Fху О В1 , заключенный между
проекциями начала и конца силы F на эту
плоскость
Модуль проекции | Fху | | F | соs .
z
А
Fу
О
Fх
х
В
F
j
Fху
В1
у
Проекции силы на ось часто находят методом двойного
проектирования, т.е. сначала проектируют силу на плоскость, а
затем на оси:
Fx | Fху | cosj | F | cos cosj , Fу | Fху | sinj | F | cos sinj .

10.

Другой метод – метод прямого
проектирования:
Fх | F | соs ,
Fу | F | соsb ,
Fz | F | соsg .
z/
z
Fx
Fz
А
g
F
b Fу
у/
х/
х
О
у

11. в) Аналитический способ задания сил

z/
Утверждение. Для того чтобы задать
силу аналитически достаточно задать
ее проекции на оси координат.
z
Fz
А
Пространственный случай.
Пусть заданы проекции силы F на
оси координат Fх , Fу , Fz ,
х/
х
Fx
g
О
Модуль силы определится в виде: F F 2х F 2у F 2z
Косинусы углов , b и g (направляющие косинусы) :
cos Fх / | F |, cosb Fу / | F |, cosg Fz / | F | .
F
b Fу
у/
у

12.

у
Плоский случай.
Пусть заданы проекции силы F на оси
координат Fх , Fу .
Модуль силы и угол найдем из формул
2
2
F F х F у,
cos Fх / | F | .
Аналитический способ сложения сил
Fу
О
F
Fх
Аналитический способ сложения сил базируется на теореме:
Теорема 1. Проекция вектора суммы на какую - нибудь ось
равна алгебраической сумме проекций слагаемых векторов
на ту же ось, то есть, если а аk , то ах = ∑ аk х .
х

13.

Сложение пространственной системы сил
Пусть силы F1 , F2 ,..., Fn заданы аналитически, т.е. известны
проекции сил на оси координат: F1х ,F2х , …,Fnх; F1у , F2у ,…,Fnу ;
F1z , F2z , …, Fnz .
Тогда, в соответствии с Теоремой 1, если R Fk , то
Rх = ∑ Fкх , Rу = ∑ Fку , Rz = ∑ Fкz .
Вычислив Rх , Rу , R z , найдем модуль | R |
R
Rх R у Rz
2
2
2
Направляющие косинусы
углов , b и g - в виде:
cos Rх / | R |, cosb Rу / | R |, cosg Rz / | R | .

14.

ЗАДАНИЕ № 16
Вдоль ребер единичного куба направлены три силы: F1= 2 Н,
F2 = F3 = 1 (Н).
Угол, который образует главный вектор системы сил с
осью Ох, равен = arccos…
ВАРИАНТЫ ОТВЕТОВ:
1) – 1 Н
2) 0 Н
3) -0,5 Н
4) 2 /2 Н
Проекции главного вектора на оси координат
Rx = - F2 = -1; Rу = - F3 = -1; Rz = - F1 = - 2 .
Модуль главного вектора
cos = Rx / | R | = - 0,5.
| R | Rх2 Rу2 Rz2 2.
= arсcos(-0,5).

15.

Сложение плоской системы сил
Пусть силы F1 , F2 ,..., Fn лежат в одной плоскости и заданы
аналитически, т.е. известны проекции сил на оси координат:
F1х , F2х , …, Fnх; F1у , F2у , …,Fnу .
Тогда, в соответствии с Теоремой 1, если
R Fk , то Rх = ∑ Fкх , Rу = ∑ Fку .
Вычислив Rх , Rу , найдем R
у
2
2
R х R у . Rу
Направляющие косинусы:
cos Rх / | R |, cosb Rу / | R | .
О
b
R
Rх
х

16. Тема 6. Равновесие сходящейся системы сил

Ранее был сделан вывод. Система сходящихся сил имеет
равнодействующую, равную геометрической сумме
(главному вектору) этих сил и приложенную в точке
пересечения их линий действия.
Вывод. Для равновесия сходящейся системы сил,
приложенной к твердому телу, необходимо и достаточно,
чтобы равнодействующая , а следовательно, и главный
вектор сил были равны нулю.
Условия, которым при этом должны удовлетворять сами
силы, можно выразить в геометрической или в
аналитической форме.

17.

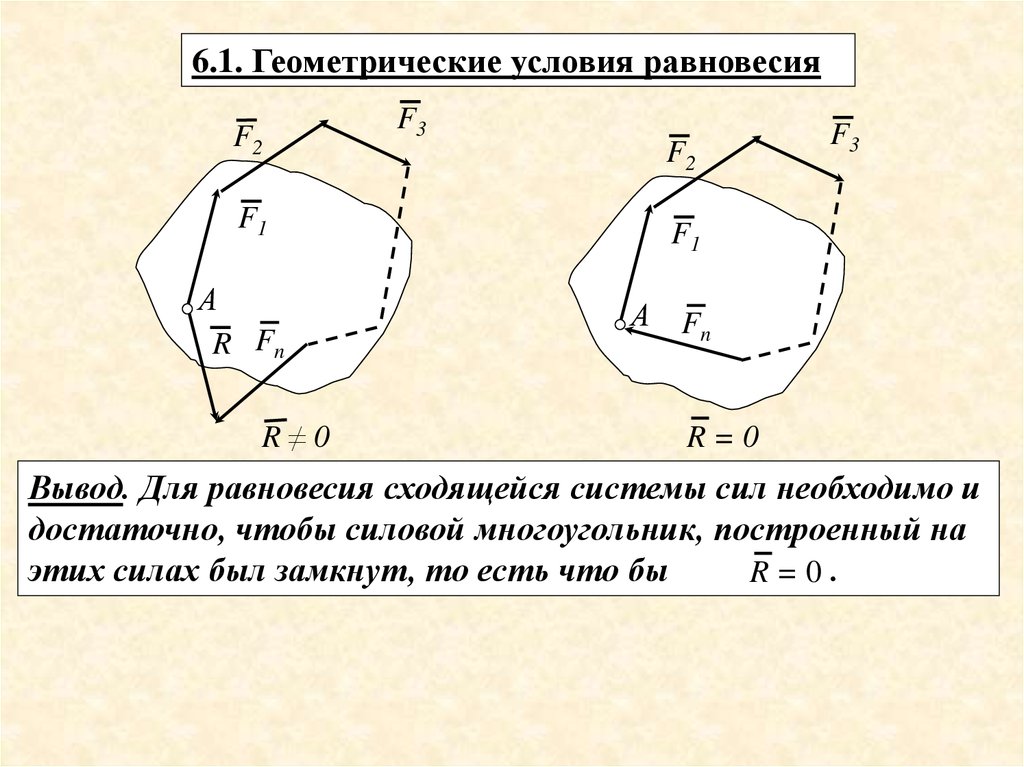
6.1. Геометрические условия равновесия
F2
F1
А
R Fn
R≠0
F3
F2
F3
F1
А Fn
R=0
Вывод. Для равновесия сходящейся системы сил необходимо и
достаточно, чтобы силовой многоугольник, построенный на
этих силах был замкнут, то есть что бы
R=0.

18.

6.2. Аналитические условия равновесия
Случай пространственной сходящейся системы сил
Аналитически модуль главного вектора системы сил
определяется формулой: R R2х R2у R2z .
Равенство нулю возможно только в случае, когда Rх , Rу , Rz
одновременно равны нулю, то есть когда одновременно
Rх = 0, Rу = 0, R z = 0.
Проекции главного вектора на оси координат:
Rх = ∑ Fкх , Rу = ∑ Fку , Rz = ∑ Fкz .
Для сходящейся системы сил главный вектор совпадает с
равнодействующей

19.

Для сходящейся системы сил главный вектор совпадает с
равнодействующей, поэтому при равновесии пространственной
сходящейся системы сил имеем условия
Rx = ∑ Fкх = 0,
Rу = ∑ Fку = 0,
Rz = ∑ Fкz = 0 .
(*)
Равенства (*) выражают условия равновесия в аналитической
форме пространственной сходящейся системы сил.
Вывод: для равновесия пространственной сходящейся системы
сил необходимо и достаточно, чтобы суммы проекций этих сил
на каждую из трех координатных осей были равны нулю.

20.

Случай плоской сходящейся системы сил
Если сходящаяся система сил является плоской, то вместо
трех условий (*) имеем только два условия равновесия
∑ Fкх = 0,
(**)
∑ Fку = 0.
Равенства (**) выражают условия равновесия в
аналитической форме плоской сходящейся системы сил.

21.

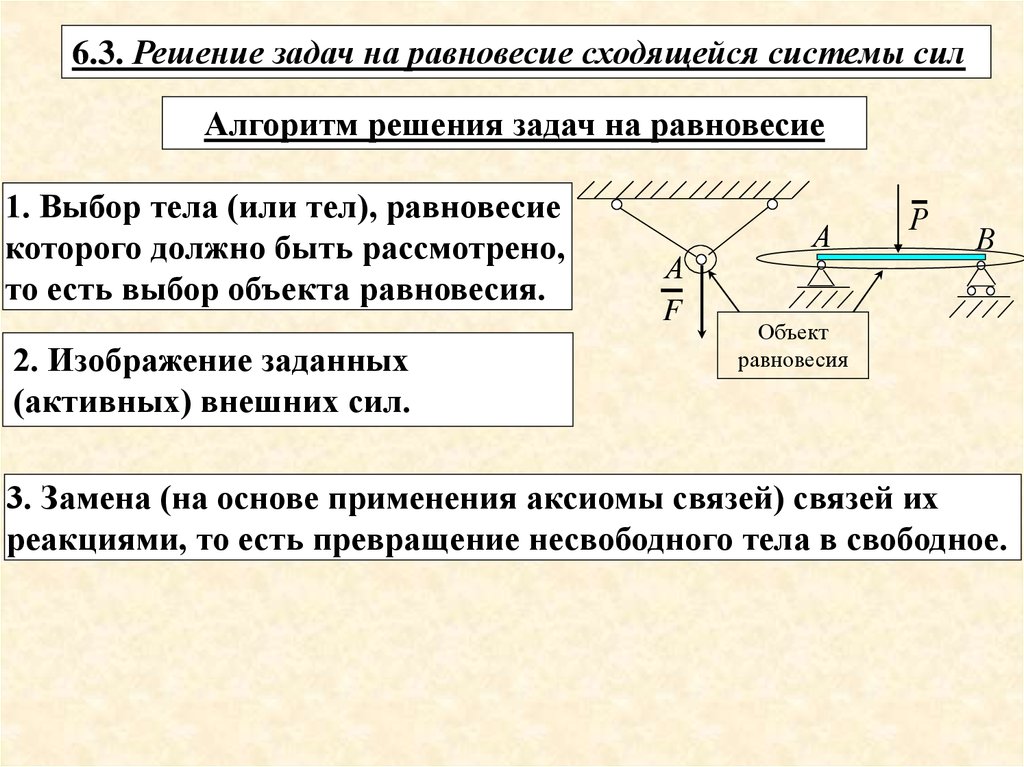
6.3. Решение задач на равновесие сходящейся системы сил
Алгоритм решения задач на равновесие
1. Выбор тела (или тел), равновесие
которого должно быть рассмотрено,
то есть выбор объекта равновесия.
2. Изображение заданных
(активных) внешних сил.
А
F
А
Р
В
Объект
равновесия
3. Замена (на основе применения аксиомы связей) связей их
реакциями, то есть превращение несвободного тела в свободное.

22.

4. Составление уравнений равновесия для системы сил,
приложенной к свободному твердому телу.
5. Определение искомых величин.
6. Проверка правильности решений и исследование
полученных результатов.

23.

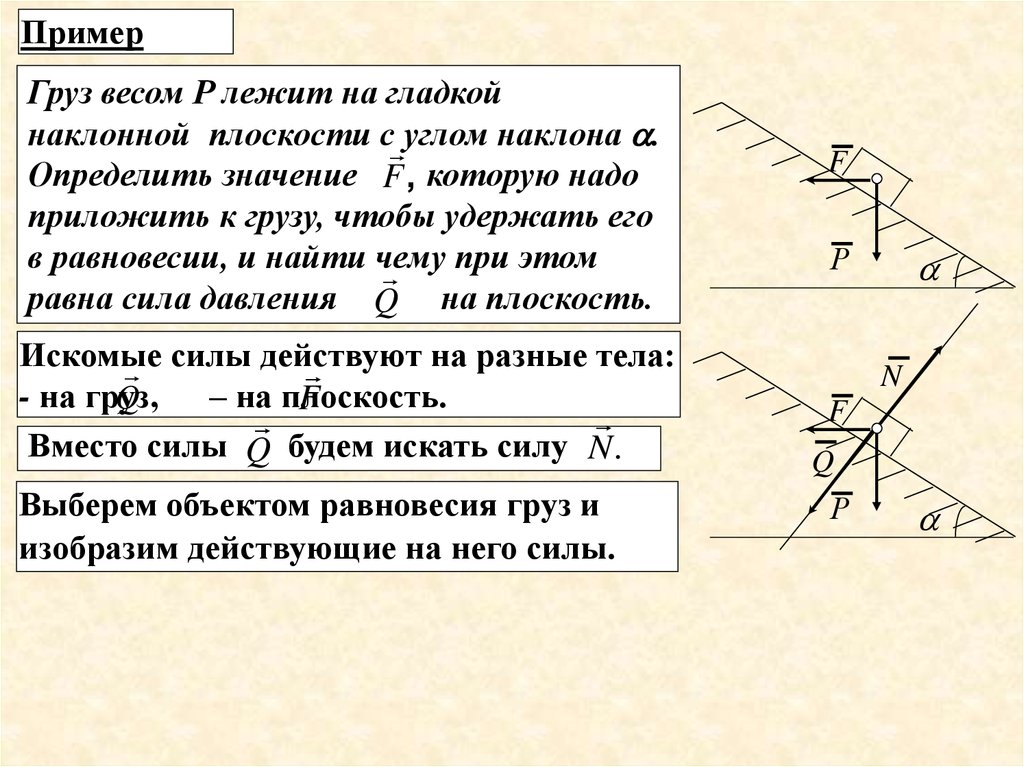
Пример
Груз весом Р лежит на гладкой
наклонной плоскости с углом наклона .
Определить значение F , которую надо
приложить к грузу, чтобы удержать его
в равновесии, и найти чему
при этом
равна сила давления Q на плоскость.
Искомые
на разные тела:
силы действуют
- на груз,
– на плоскость.
Q
F
Вместо силы Q будем искать силу N.
Выберем объектом равновесия груз и
изобразим действующие на него силы.
F
Р
N
F
Q
Р

24.

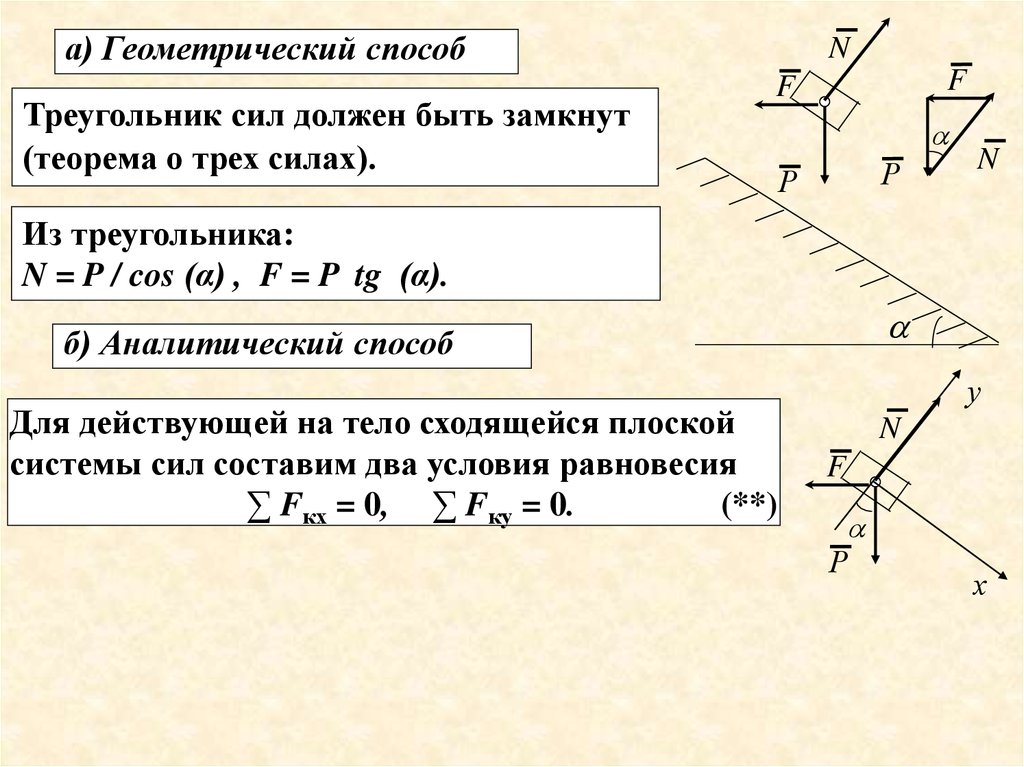
а) Геометрический способ
Треугольник сил должен быть замкнут
(теорема о трех силах).
N
F
F
Р
Р
N
Из треугольника:
N = P / cos (α) , F = P tg (α).
б) Аналитический способ
Для действующей на тело сходящейся плоской
системы сил составим два условия равновесия
∑ Fкх = 0, ∑ Fку = 0.
(**)
у
N
F
Р
х

25.

Составим таблицу проекций сил на оси.
Fk
Р
F
N
Р sin a
- F cos a
0
Fкх
Fку
- Р cos a
- F sin a
N
Уравнения (**) имеют вид:
∑ Fкх = Р sin - F cos 0,
у
Fx N
F
F
Pу у
Р
Px
х
∑ Fку = - Р cos - F sin N 0.
Решая систему уравнений, получим: N = P / cos (α), F = P tg (α).
Замечание. Рассмотренный алгоритм решения задач на
равновесие применяется не только для сходящихся систем сил,
но и для любых систем сил.

26.

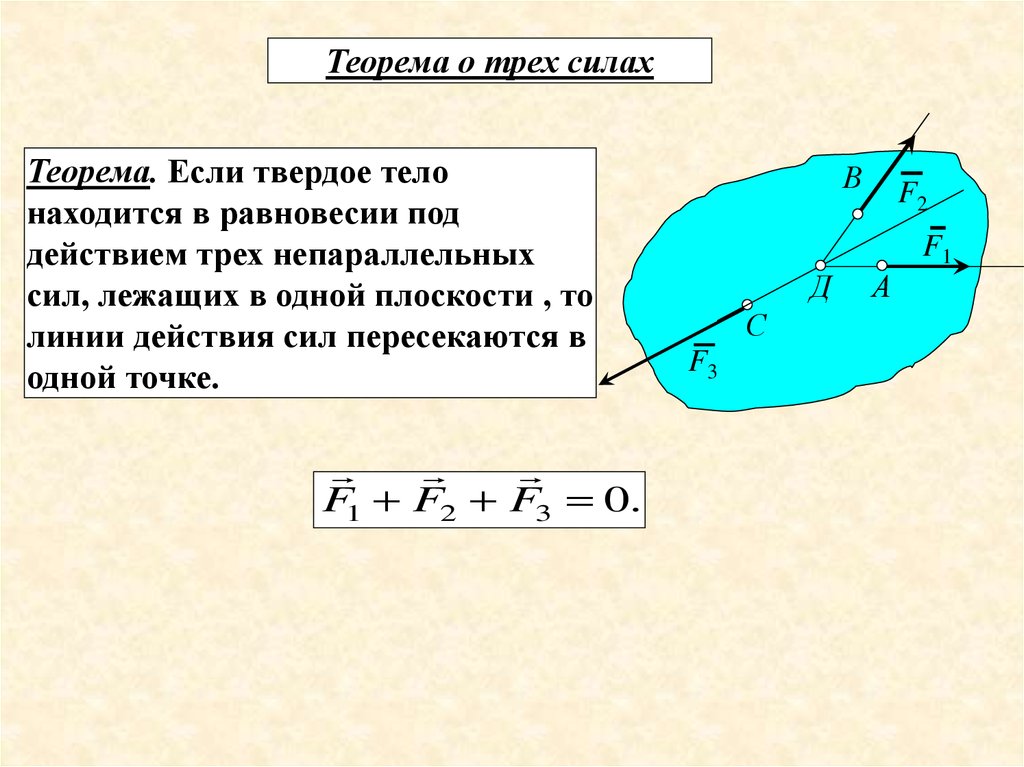
Теорема о трех силах
Теорема. Если твердое тело
находится в равновесии под
действием трех непараллельных
сил, лежащих в одной плоскости , то
линии действия сил пересекаются в
одной точке.
F1 F2 F3 0.
В
F2
F1
Д
С
F3
А

27.

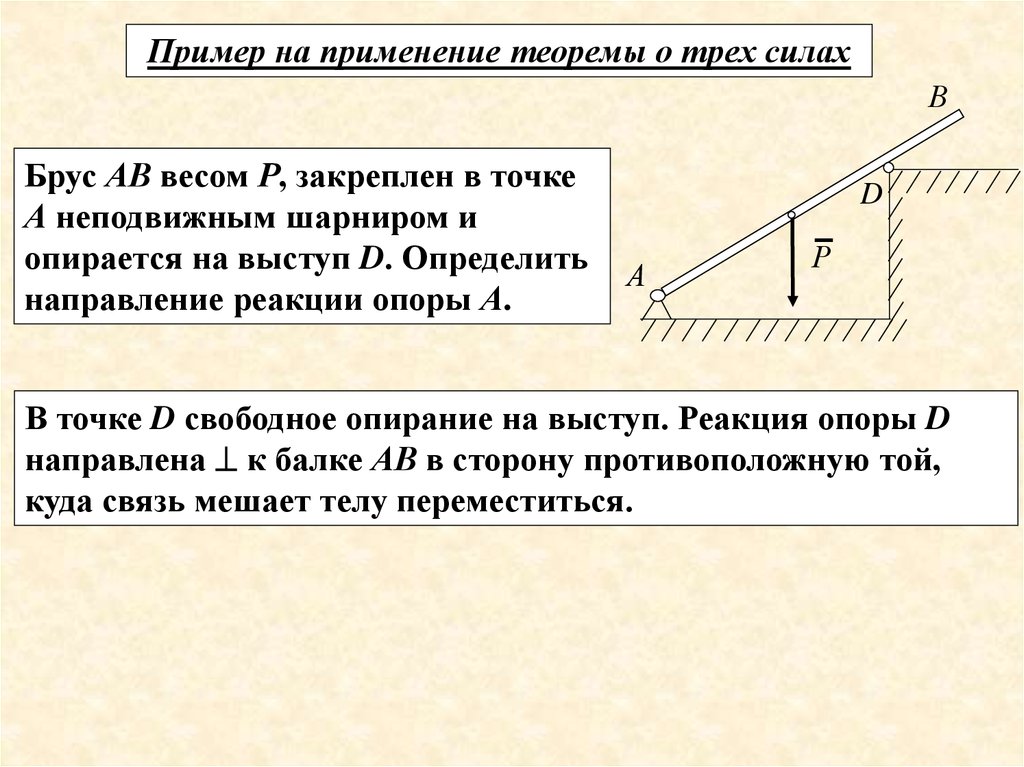
Пример на применение теоремы о трех силах
В
Брус АВ весом Р, закреплен в точке
А неподвижным шарниром и
опирается на выступ D. Определить
направление реакции опоры А.
D
А
Р
В точке D свободное опирание на выступ. Реакция опоры D
направлена к балке АВ в сторону противоположную той,
куда связь мешает телу переместиться.

28.

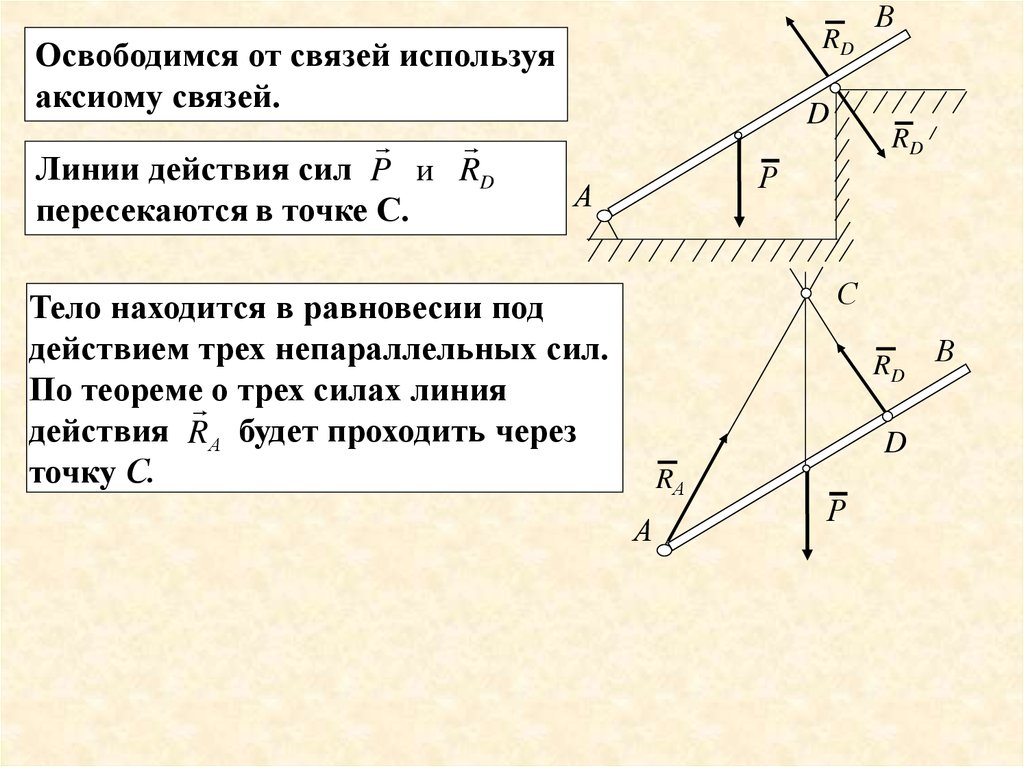
RD
Освободимся от связей используя
аксиому связей.
Линии действия сил P и RD
А
пересекаются в точке С.
D
В
RD /
Р
С
Тело находится в равновесии под
действием трех непараллельных сил.
По теореме о трех силах линия
действия RА будет проходить через
точку С.
RD
D
RА
А
Р
В