Пространственная система сил

1.

СТАТИКА
10. Пространственная система сил

2.

10.1.Вычисление модулей главного вектора и главного момента
Теорема о приведении системы сил:
Любая система сил, действующих на абсолютно твердое
тело, при приведении к произвольно
выбранному центру О
заменяется одной силой R, равной главному вектору
системы сил и приложенной
в центре приведения О, и
одной парой с моментом М 0 , равным главному моменту
системы сил относительно центра О.
Главный момент системы
центра О сил относительно
М О mO(Fk ).
Главный вектор системы сил R Fk .
заданы аналитически, т.е.
Пусть силы F1 , F2 ,...., Fn
известны проекции сил на оси координат: F1х ,F2х , …,Fnх;
F1у , F2у , …,Fnу ; F1z , F2z , …, Fnz .

3.

Тогда проекции главного вектора на оси координат
определятся по формулам
Rх = ∑ Fкх , Rу = ∑ Fку , Rz = ∑ Fкz .
(1)
Проекции главного момента - по формулам
МОх = ∑ mОх (Fк ), МОу = ∑ mОу (Fк ), , МОz= ∑ mОz (Fк ) .
(2)
Модули главного вектора и главного момента
R R2х R2у R2z ;
2
2
2
М 0 М ох
М оу
М оz
;
(3)

4.

10.2.Условия равновесия произвольной пространственной
системы сил
В случае равновесия произвольной пространственной
системы сил главный вектор и главный момент равны нули,
то есть R = 0 и МО = 0 .
Следовательно, равны нулю и их модули: |R | = 0, |МО| = 0 ,
2
2
2
2
2
2
то есть R R х R у R z 0, М 0 М ох М оу М оz 0. (4)
Так как подкоренные выражения не могут быть
отрицательными, то условия (4) могут выполнятся только
в случаях, если
Rх = 0 , Rу = 0, Rz = 0 .
(5)

5.

МОх = 0,
МОу = 0,
МОz= 0 .
(6)
или, с учетом формул (1) и (2)
∑ Fкх = 0 ,
∑ Fку = 0 ,
∑ Fкz = 0,
mOx ( F k ) 0,
mOу ( F k ) 0,
mOz ( Fk ) 0.
Вывод. Для равновесия произвольной пространственной
системы сил необходимо и достаточно, чтобы суммы
проекций всех сил на каждую из трех координатных осей и
суммы их моментов относительно этих осей были равны нулю.

6.

10.3. Случай параллельных сил
z
Если все действующие силы
параллельны друг другу, то можно
выбрать координатные оси так, что
ось Оz , будет параллельна силам.
Тогда проекции каждой из сил на оси х
Ох и Оу и их моменты относительно
оси Оz будут равны нулю и система
(7) даст три условия равновесия:
F1
О
F2
∑ Fкz = 0,
mOу ( Fk ) 0 ,
mOz ( Fk ) 0.
Остальные равенства обратятся в тождества (0 ≡ 0).
F3
Fn
у

7.

Вывод. Для равновесия пространственной системы
параллельных сил необходимо и достаточно, чтобы сумма
проекций всех сил на ось параллельную силам, и сумма их
моментов относительно двух других координатных осей
были равны нулю.
10.4. Пример решения задач на равновесие произвольной
пространственной системы сил.

8.

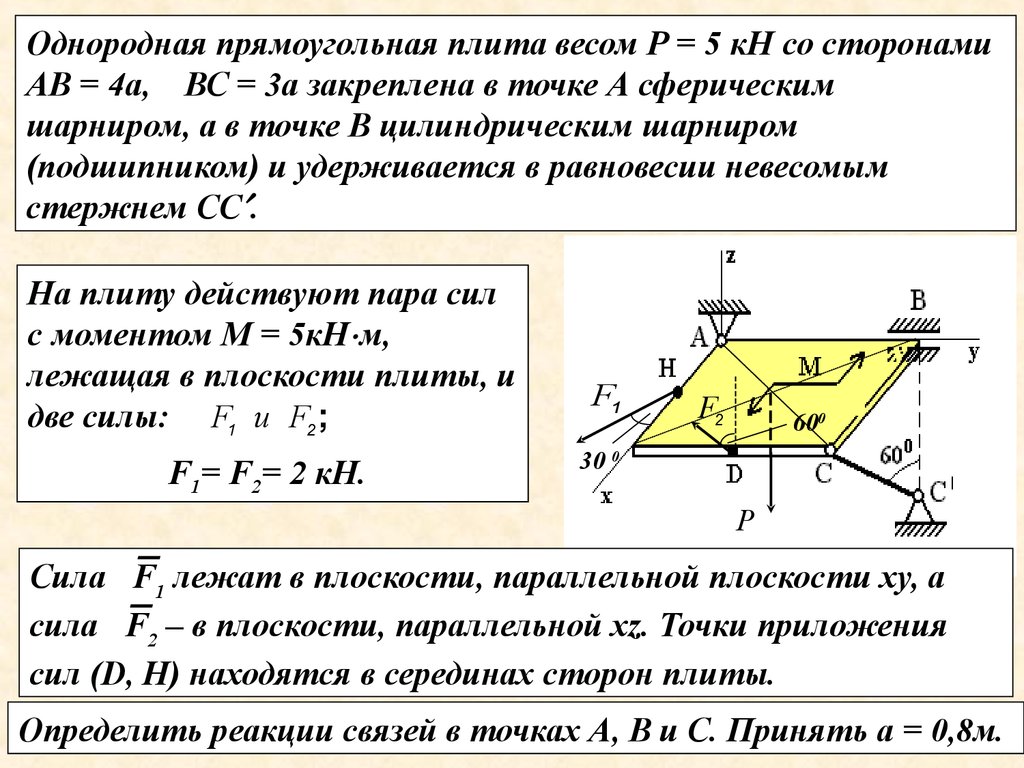
Однородная прямоугольная плита весом Р = 5 кН со сторонами
АВ = 4а, ВС = 3а закреплена в точке А сферическим
шарниром, а в точке В цилиндрическим шарниром
(подшипником) и удерживается в равновесии невесомым
стержнем СС .
На плиту действуют пара сил
с моментом М = 5кН м,
лежащая в плоскости
плиты, и
две силы: F1 и F2 ;
F1= F2= 2 кН.
F1
F2
600
30 0
Р
Сила F1 лежат в плоскости, параллельной плоскости ху, а
сила F2 – в плоскости, параллельной хz. Точки приложения
сил (D, H) находятся в серединах сторон плиты.
Определить реакции связей в точках А, В и С. Принять а = 0,8м.

9.

Решение .
1.Выберем объект равновесия.
Плита.
2. Приложим к объекту
равновесия заданные силы.
Силы Р, F1 , F2 и пара сил с
моментом М .
ZA
F1
30
F2
ХА
ZВ
УА
ХВ
600
600
0
Р
S
3. Освободимся от связей.
В точке А сферический
шарнир, который заменяется тремя
реакциями Х А , У А и Z А .
В точке В цилиндрический
шарнир, который заменяется
двумя реакциями Х В , и Z В .
Усилие в невесомом стержне СС / - S направлено вдоль
стержня.

10.

4. Составим уравнения равновесия.
Предварительно, в целях
применения теоремы
Вариньона о моменте
равнодействующей, разложим
наклонные силы на
составляющие, направленные
параллельно осям координат.
F1 у
F1
30
0
ZA
Х А
F2 z
600
F2
F1 x F2 у
ZВ
УА
ХВ
Sx
600
Р
Sz
S
А) Уравнения проекций.
0
0
F
X
X
F
cos
30
S
cos60
0,
kx
A
B
1
F
F
kу
kz
У А F1 cos60 0 F2 cos300 0,
Z A Z B F2 cos600 S cos30 0 Р 0.
(1)
(2)
(3)

11.

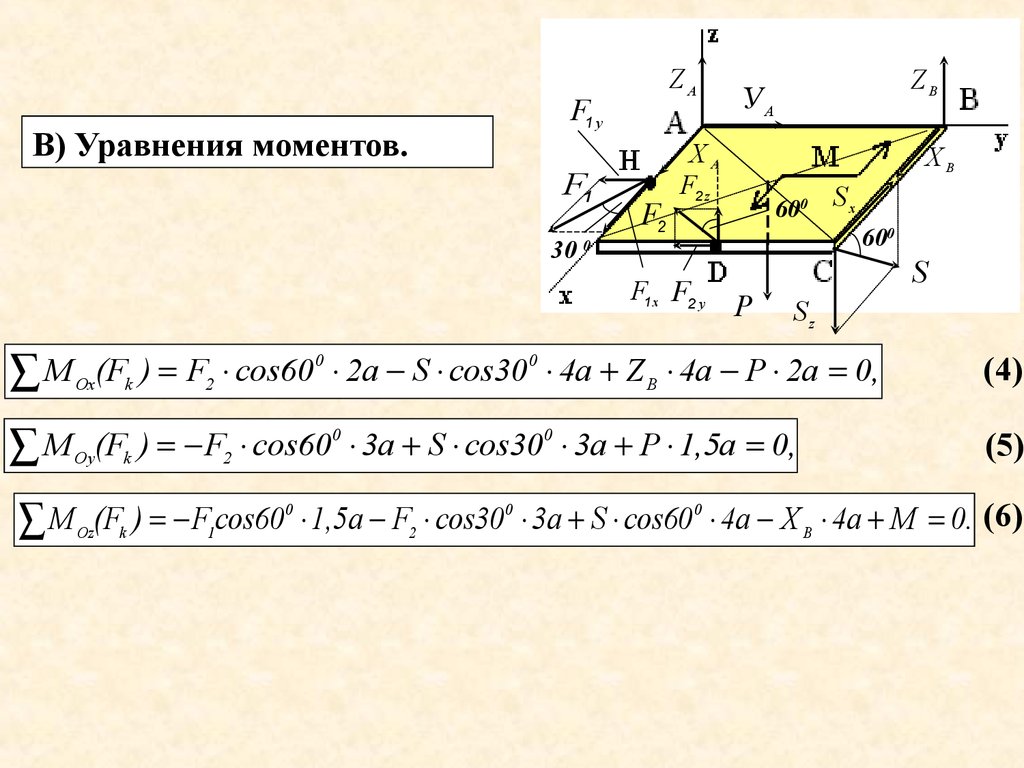
В) Уравнения моментов.
F1 у
F1
30
0
ZA
Х А
F2 z
600
F2
F1 x F2 у
ZВ
УА
ХВ
Sx
600
Р
Sz
S
(4)
М Ох(Fk ) F2 cos600 2a S cos300 4a Z B 4a Р 2а 0,
(5)
М Оу(Fk ) F2 cos600 3a S cos300 3a Р 1,5а 0,
М Оz(Fk ) F1cos600 1,5a F2 cos300 3a S cos600 4a X B 4a M 0. (6)

12.

4. Решение системы уравнений (1) – (6).
Из уравнения (2) найдем УА= 2,73 кН.
Из уравнения (5) найдем S = - 2,89 кН.
Из уравнения (4) найдем ZB = - 0,5 кН.
Из уравнения (6) найдем XB = - 1,56 кН.
Из уравнения (1) найдем XA = - 1,6 кН.
Из уравнения (3) найдем ZA = 1,0 кН.
Реакции S, ZB , XB , XA в стороны противоположные
изображенным на рисунке.