Пространственная система сил. Центр тяжести

1.

Тема 8.
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ. ЦЕНТР ТЯЖЕСТИ.
Для задания любой пространственной системы сил,
действующих на твёрдое тело, достаточно определить её
главный вектор R и главный момент M0 относительно
некоторого центра, т. е. шесть величин из равенств ниже.
RX FkX , M 0 X m0 X (Fk )
RY FkY , M 0Y m0Y (Fk )
RZ FkZ , M 0 Z m0 Z (Fk )
1

2.

8.1. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К
ПРОСТЕЙШЕМУ ВИДУ.
Необходимые и достаточные условия равновесия любой системы
сил выражаются равенствами R = 0, М0 = 0.
Векторы R и М0 равны нулю только тогда, когда
RX = RY = RZ = 0 и МX = МY = МZ = 0,
т. е. когда действующие силы будут удовлетворять условиям:
RX FkX 0, M 0 X m0 X (Fk ) 0
RY FkY 0, M 0Y m0Y (Fk ) 0
RZ FkZ 0, M 0 Z m0 Z (Fk ) 0
Для равновесия произвольной пространственной
системы сил необходимо и достаточно, чтобы суммы
проекций всех сил на каждую из трёх координатных
осей и суммы их моментов относительно этих осей
2
были равны нулю.

3.

8.1. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К
ПРОСТЕЙШЕМУ ВИДУ.
Случай параллельных сил .
В случае, когда все действующие на тело силы
параллельны друг другу, можно выбрать координатные оси
так, что ось z будет параллельна силам. Тогда проекции
каждой из сил на оси х и у и их моменты относительно оси z
будут равны нулю и система уравнений равновесия в этом
случае будет содержать три равенства:
RZ FkZ 0, M 0 X m0 X (Fk ) 0, M 0Y m0Y (Fk ) 0
Следовательно, для равновесия пространственной
системы параллельных сил необходимо и достаточно,
чтобы сумма проекций всех сил на ось, параллельную
силам, и суммы их моментов относительно двух
других координатных осей были равны нулю.
3

4.

8.1. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К
ПРОСТЕЙШЕМУ ВИДУ.
Пример решения задачи.
На горизонтальный вал, лежащий в подшипниках А и В
насажены перпендикулярно оси вала шкив радиусом r1 = 20
см и барабан радиусом r2 = 15 см. Вал приводится во
вращение ремнём, накинутым на шкив; при этом равномерно
поднимается груз весом Р = 540 Н, привязанный к верёвке,
которая наматывается на барабан.
Пренебрегая весом вала,
барабана и шкива, определить
реакции подшипников А и В и
натяжение T1 ведущей ветви
ремня, если известно, что оно
вдвое больше натяжения T2
ведомой ветви.
Дано: а = 40 см, b =60 см, =30°.
4

5.

8.1. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К
ПРОСТЕЙШЕМУ ВИДУ.
Решение.
В данной задаче при равномерном вращении вала
действующие на него силы удовлетворяют условиям
равновесия:
FkX 0, m0 X (Fk ) 0
FkY 0, m0Y (Fk ) 0
FkZ 0, m0 Z (Fk ) 0
Проведём координатные оси как показано на рисунке.
Укажем действующие на вал силы:
- сила натяжения верёвки F, по модулю она равна весу груза P;
- сила натяжения ремня T1 и T2;
- силы реакции подшипников RA и RB, которые разложим на
составляющие по осям YA, ZA, YB, ZB.
5

6.

8.1. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К
ПРОСТЕЙШЕМУ ВИДУ.
Решение.
Определим проекции всех сил на координатные оси и их
моментов относительно этих осей. Это нам понадобится для
составления условий равновесия пространственной системы
сил.
Fk
F
T1
T2
RA
RB
Fkx
0
0
0
0
0
Fky
Fcos
T1
T2
YA
YB
Fkz
-Fsin
0
0
ZA
ZB
mx(Fk)
-F∙r2
T1∙r1
-T2∙r1
0
0
my(Fk)
Fsin ∙b
0
0
0
-ZB(a+b)
mz(Fk)
Fcos ∙b
-T1∙a
-T2∙a
0
YB(a+b)
6

7.

8.1. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К
ПРОСТЕЙШЕМУ ВИДУ.
Решение.
Составим систему уравнений равновесия для данного
случая. Y : P cos T1 T2 YA YB 0
Z : P sin Z A Z B 0
m Ax : r2 P r1 T1 r1 T2 0
m Ay : b P sin (a b) Z B 0
m Az : b P cos a T1 a T2 (a b) YB 0
7

8.

8.1. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К
ПРОСТЕЙШЕМУ ВИДУ.
Решение.
Решим эту систему уравнений и определим неизвестные
величины.
Учтём, что T1 2T2 , тогда из уравнений третьего и четвёртого
уравнений
r2 P
bP sin
T2
405 H , Z B
162 H
r1
( a b)
Из пятого уравнения найдём YB
3aT2 bP cos
YB
205 H
( a b)
Далее из первого и второго уравнения находим
YA YB 3T2 P cos 1890 H , Z A P sin Z B
8

9.

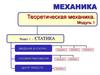
8.2. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЁРДОГО ТЕЛА.
Область, в каждой точке которой на помещённую туда
материальную частицу действует сила, зависящая от
положения (координат) этой точки, называется
силовым полем.
На каждую частицу тела,
находящегося вблизи земной
поверхности, действует направленная
вертикально вниз сила, которую
называют силой тяжести. Эти силы
образуют поле сил тяжести.
Для тел, размеры которых очень малы по
сравнению с земным радиусом, силы
тяжести можно считать параллельными друг другу и
сохраняющими для каждой частицы постоянное значение при
любых поворотах тела. Поле тяжести, в котором
выполняются эти два условия, называют однородным
полем тяжести.

10.

8.2. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЁРДОГО ТЕЛА.
Область, в каждой точке которой на помещённую туда
материальную частицу действует сила, зависящая от
положения (координат) этой точки, называется
силовым полем.
Равнодействующую сил тяжести
р1, р2 … рn, действующих на частицы
данного тела, обозначим Р. Модуль этой
силы называется весом тела и
определяется равенством
P pk
Центром тяжести твёрдого тела называется
неизменно связанная с этим телом точка, через которую
проходит линия действия равнодействующей сил
тяжести, действующих на частицы данного тела, при
любом положении тела в пространстве.
10

11.

8.2. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЁРДОГО ТЕЛА.
Координаты центра тяжести определяются формулами
1
1
1
xC pk xk , yC pk yk , zC pk zk .
P
P
P
где xk, yk, zk — координаты точек приложения сил тяжести рk,
действующих на частицы тела.
Согласно определению центр тяжести — это точка
геометрическая; она может лежать и вне пределов данного
тела.
8.3. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ.
Положение центра тяжести однородного тела зависит только от
его геометрической формы.
Координаты центра тяжести объёма можно определить по
формулам
1
1
1
xC
vk xk ,
V
yC
vk yk ,
V
zC
где V – объём всего тела, k – объём его частей.
vk zk ,
V

12.

8.3. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ.
Если тело представляет собой однородную плоскую и тонкую
пластину, то координату точки центра тяжести площади
S можно найти по формулам
1
1
xC sk xk , yC sk yk ,
S
S
где S – объём всего тела, sk – объём его частей.
Формулы для координат центра тяжести линии:
1
1
1
xC lk xk , yC lk yk , zC lk zk .
L
L
L
где L – объём всего тела, lk – объём его частей.
Таким образом, центр тяжести однородного тела определяется,
как центр тяжести соответствующего объёма, площади или
12
12
линии.

13.

8.4. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ
ТЕЛ.
1. Симметрия .
Если однородное тело имеет плоскость, ось или центр
симметрии, то его центр тяжести лежит соответственно или в
плоскости симметрии, или на оси симметрии, или в центре
симметрии.
2. Разбиение.
Если тело можно разбить на конечное число таких частей, для
каждой из которых положение центра тяжести известно, то
координаты центра тяжести всего тела можно
непосредственно вычислить по формулам. При этом число
слагаемых в каждой из сумм будет равно числу частей, на
которые разбито тело.
3. Дополнение.
Этот способ является частным случаем способа разбиения.
Он применяется к телам, имеющим вырезы, если центры
13
тяжести тела без выреза и вырезанной части известны. 13

14.

8.4. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ
ТЕЛ.
4. Интегрирование.
Если тело нельзя разбить на несколько конечных частей,
положения центров тяжести которых известны, то тело
разбивают сначала на произвольные малые объёмы k,
затем переходят к пределу, устремляя все k к нулю, т. е.
стягивая эти объёмы в точки. Тогда суммы в формулах для
определения координат центров тяжести объёма, площади и
линии обращаются в интегралы:
1
1
1
xC xdv, yC ydv, zC zdv,
VV
VV
VV
1
1
xC xds, yC yds,
SS
SS
1
1
1
xC xdl , yC ydl , zC zdl.
LL
LL
LL
14

15.

8.5. ОПРЕДЕЛЕНИЕ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
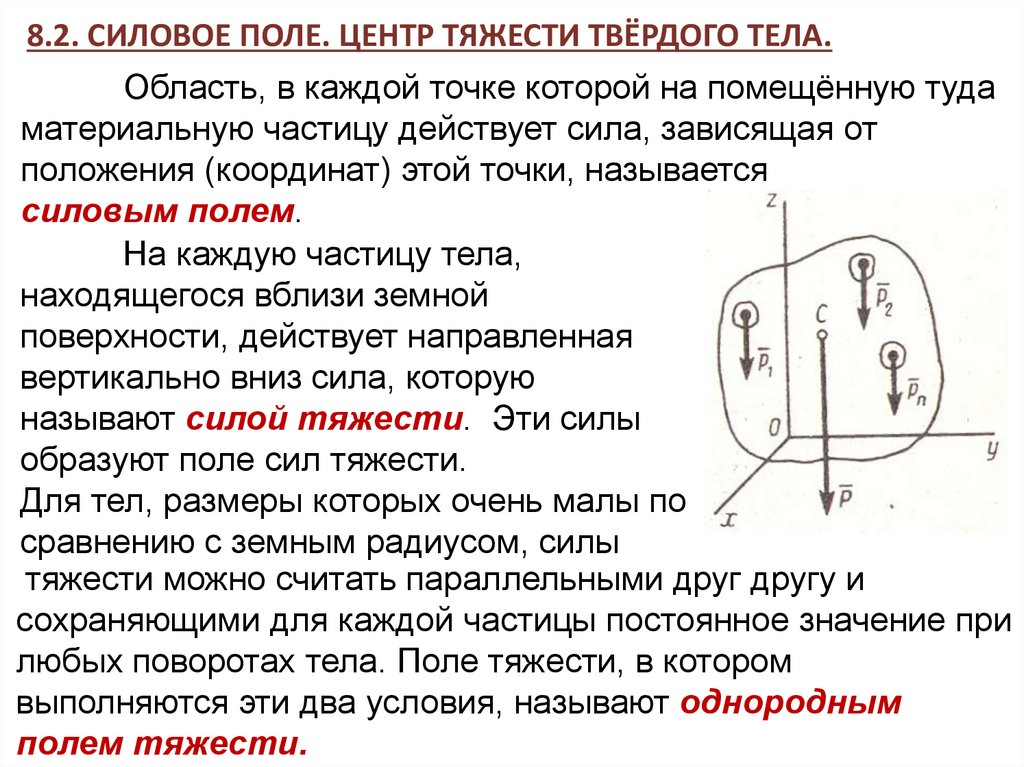
Задача 1.
Определить координаты центра тяжести однородной пластины,
изображённой на рисунке. Все размеры даны в сантиметрах.
Решение.
Проводим оси х, у и разбиваем пластину на три прямоугольника
(линии разреза показаны на рисунке). Вычисляем координаты
центров тяжести каждого из прямоугольников и их площади (см.
таблицу).
15

16.

8.5. ОПРЕДЕЛЕНИЕ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
Решение.
Площадь всей пластины
S s1 s2 s3 36 см 2
Подставим вычисленные величины в формулы для расчёта
координаты центра тяжести площади
x1s1 x2 s2 x3 s3 4 20 60
xC
0,22 см
S
36
y1s1 y2 s2 y3 s3 4 100 108
yC
4,44 см
S
36
Найденное положение центра тяжести С показано на чертеже;
точка С оказалась вне пластины.
16

17.

8.5. ОПРЕДЕЛЕНИЕ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
Задача 2.
Определить положение центра тяжести круглой пластины радиуса R с
вырезом радиуса r . Расстояние С1С2= а.
Решение.
Линия C1С2 является осью симметрии фигуры, центр
тяжести пластины лежит на этой линии.
Проводим координатные оси как показано на рисунке к
задаче.
Для нахождения координаты Xс дополним площадь
пластины до полного круга (часть 1), а затем вычтем из
полученной площади площадь вырезанного круга
(часть 2).
2
2
s1 R , s2 r , S s1 s2 , x1 0, x2 a
S R2 r 2 ,
x1s1 x2 s2
ar 2
xc
2 2 ; yc 0.
S
R r
17
17

18.

8.6. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ.
1. Центр тяжести дуги окружности.
Рассмотрим дугу АВ радиуса R с центральным
углом АОВ =2 .
В силу симметрии центр тяжести этой дуги лежит
на оси Ох.
Найдём координату Xс по формуле для центра
тяжести линии.
Выделим на дуге АВ элемент ММ' длиной dl=Rd .
Положение этого элемента определяется углом .
Координату элемента ММ' можно выразить как x =
R∙cos .
Подставим x и dl в формулу для расчёта центра тяжести линии
В
2
1
R
R2
xC xdl
cos d 2 sin , L R 2
LА
L
L
Центр тяжести дуги окружности лежит на её оси
симметрии на расстоянии от центра О
18
xC R sin / .

19.

8.6. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ.
2. Центр тяжести площади
треугольника.
Разобьём площадь треугольника
ABD прямыми, параллельными
стороне AD, на n узких полосок.
Центры тяжести этих полосок
будут лежать на медиане BE
треугольника.
Следовательно, и центр тяжести всего треугольника лежит
на этой медиане. Аналогичный результат получается для
двух других медиан.
Центр тяжести площади треугольника лежит в
точке пересечения его медиан.
BE
СЕ
19
19
3

20.

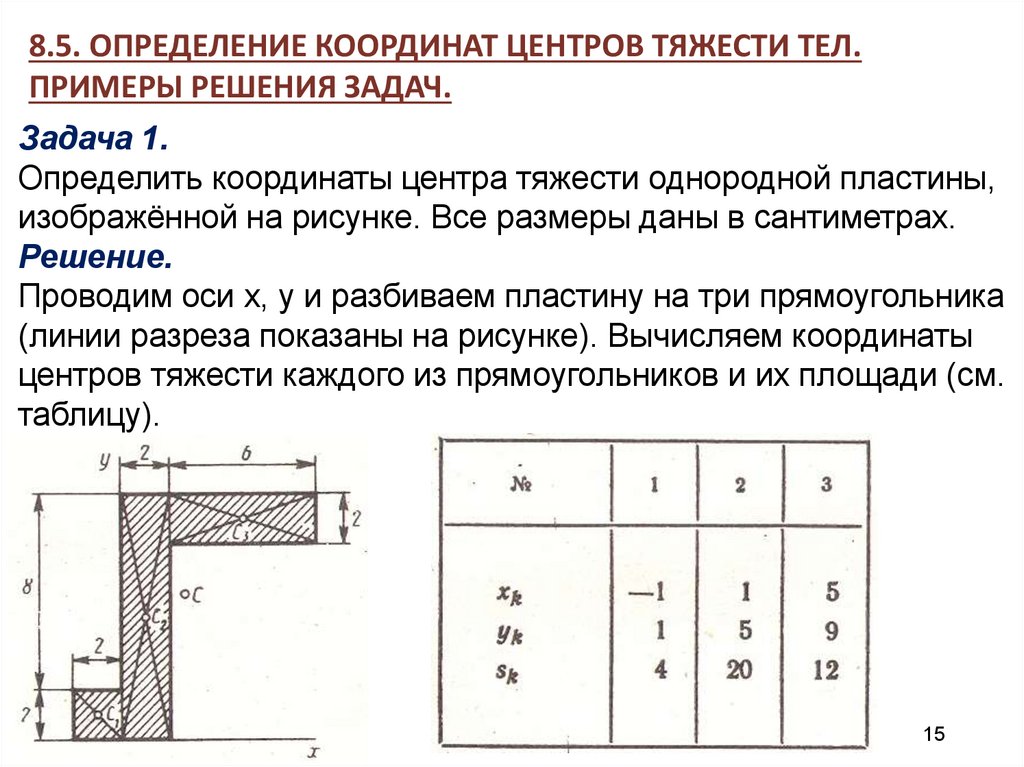
8.6. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ.
3. Центр тяжести площади
кругового сектора.
Рассмотрим круговой сектор ОАВ
радиуса R с центральным углом 2 .
Разобьём мысленно площадь сектора
ОАВ радиусами, проведёнными из
центра О, на n секторов. Эти секторы
можно рассматривать как плоские
треугольники, центры тяжести которых
лежат на дуге DE радиуса 2R/3. Следовательно, центр
тяжести сектора ОАВ совпадает с центром тяжести дуги DE.
Тогда, по формуле для центра тяжести дуги
2 R sin
xC
3
Центр тяжести площади кругового сектора лежит на
его оси симметрии на расстоянии от центра О.20

21.

8.6. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ.
4. Центр тяжести объёма пирамиды.
Этот центр С лежит на прямой С1Е, где Е вершина, а С1 - центр тяжести площади
основания пирамиды.
BE
СЕ
3
Результат справедлив для любой
многоугольной пирамиды и для конуса.
5. Центр тяжести объёма половины
шара.
Этот центр С лежит на оси Ох
(оси симметрии), а его координата
3R
xC OС
8
21