Similar presentations:
Центр тяжести
1. Центр тяжести
1.2.
3.
Понятие центра тяжести.
Теорема о центре тяжести.
Положение цт стандартных фигур.
2. 1.
Центр тяжести- это такая,неизменно связанная с телом точка,
через которую проходит линия
действия силы тяжести при любом
положении тела в пространстве.
3. Координаты центра тяжести можно найти с помощью метода разбиения.
A1 X 1 A2 X 2 ... An X nXC
A
A1 Y1 A2 Y2 ... An Yn
YC
A
Разбиваем сложную фигуру
на простые.
У каждой простой фигуры
находим координаты
центра тяжести и
площадь.
Подставляем найденные
значения в формулы и
находим координаты
общего центра тяжести.
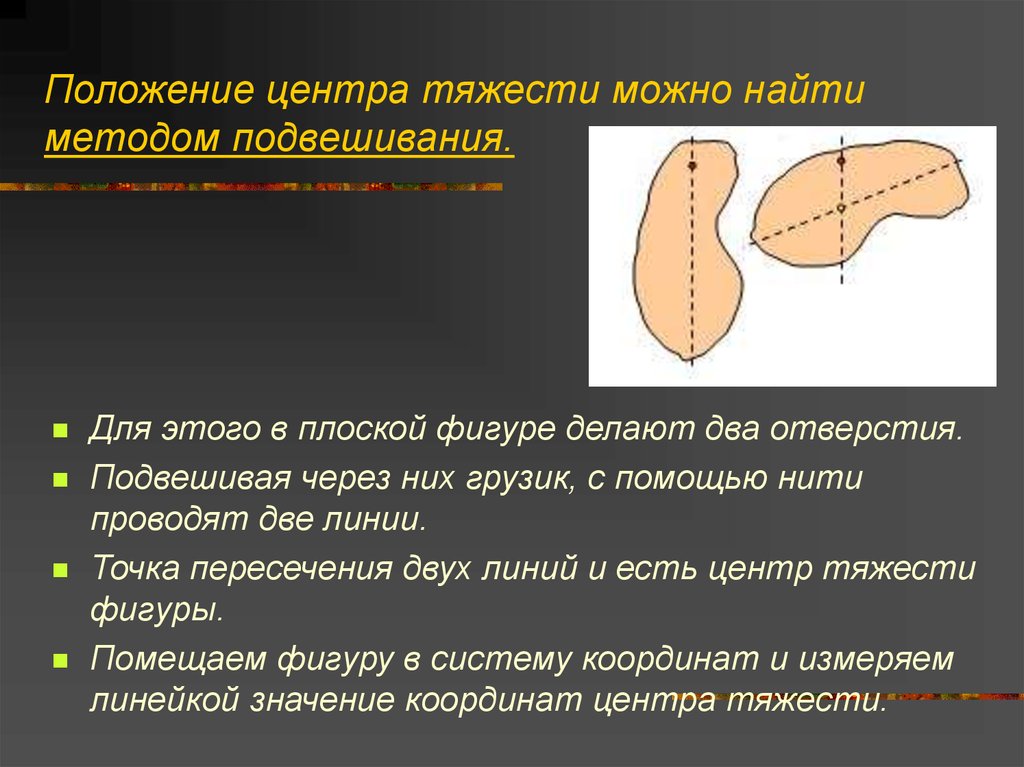
4. Положение центра тяжести можно найти методом подвешивания.
Для этого в плоской фигуре делают два отверстия.Подвешивая через них грузик, с помощью нити
проводят две линии.
Точка пересечения двух линий и есть центр тяжести
фигуры.
Помещаем фигуру в систему координат и измеряем
линейкой значение координат центра тяжести.
5. 2. Теорема о центре тяжести
«Если однородное тело имеет плоскость, ось илицентр симметрии, то центр тяжести лежит
соответственно в плоскости, на оси или в центре
симметрии.»
Следствия:
Центр тяжести отрезка лежит на его середине.
Центр тяжести параллелограмма лежит на
пересечении его диагоналей.
Центр тяжести прямоугольника, круга, эллипса
лежит в их геометрических центрах.
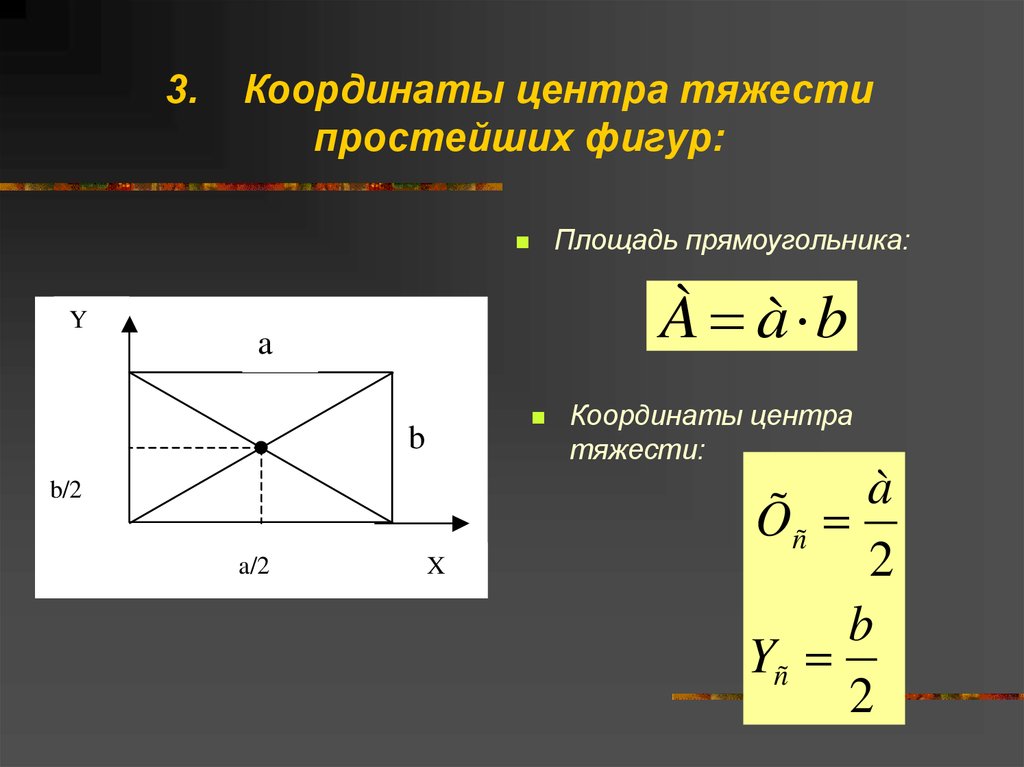
6. 3. Координаты центра тяжести простейших фигур:
Площадь прямоугольника:Y
À à b
a
b
b/2
a/2
X
Координаты центра
тяжести:
à
Õñ
2
b
Yñ
2
7.
Площадь треугольника:à b
À
2
Y
a
а/3
b/3
b
X
Координаты центра
тяжести:
b
Õñ
3
à
Yñ
3
8.
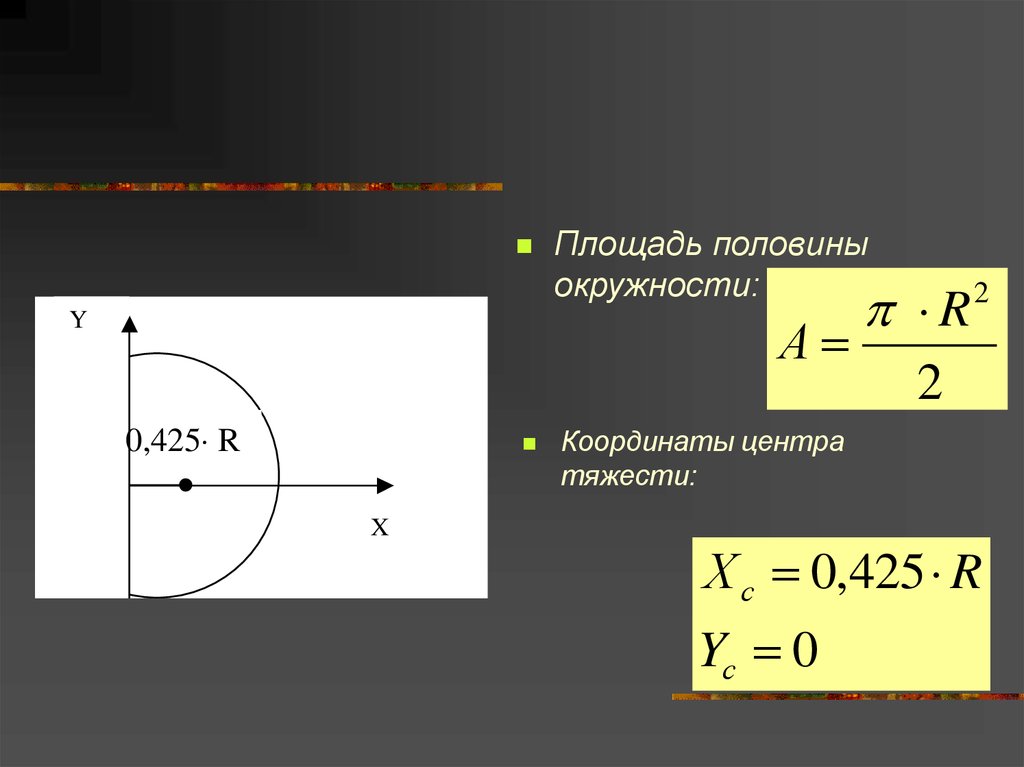
Площадь половиныокружности:
А
Y
0,425 R
X
R
2
2
Координаты центра
тяжести:
Х с 0,425 R
Yс 0





 physics
physics








