Similar presentations:
Центр тяжести и устойчивое равновесие
1. Тема: Центр тяжести и устойчивое равновесие
2. План занятия
1.2.
3.
4.
5.
Знакомство с понятием центра тяжести;
Методы нахождения центра тяжести;
Нахождение центра тяжести и площадей
простых геометрических фигур;
Нахождение центра тяжести
стандартных прокатных профилей;
Нахождение центра тяжести объемных
фигур
3. Центром тяжести называется центр параллельных сил тяжести всех элементарных частиц, из которых состоит тело.
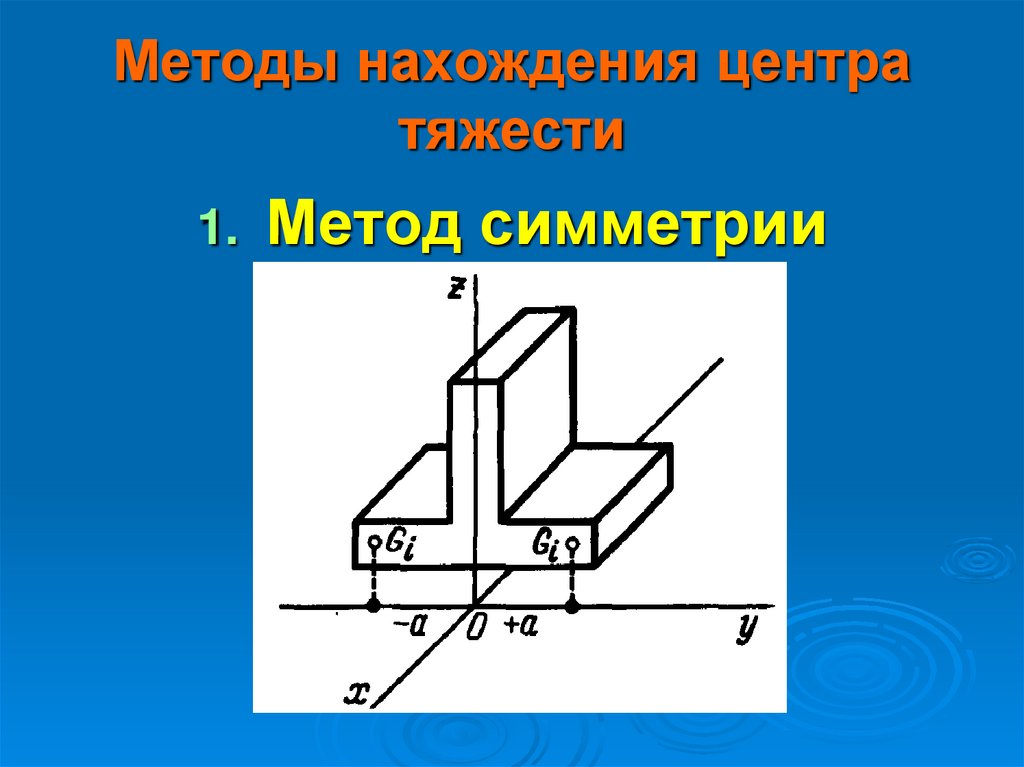
4. Методы нахождения центра тяжести
1.Метод симметрии
5. Если однородное тело имеет площадь симметрии, то центр тяжести лежит в этой плоскости.
6.
если однородное тело имеет осьсимметрии, то центр тяжести тела
лежит на этой оси;
если
однородное тело имеет 2 оси
симметрии, то центр тяжести тела
находится в точке их пересечения;
центр
тяжести однородного тела
вращения лежит на оси вращения.
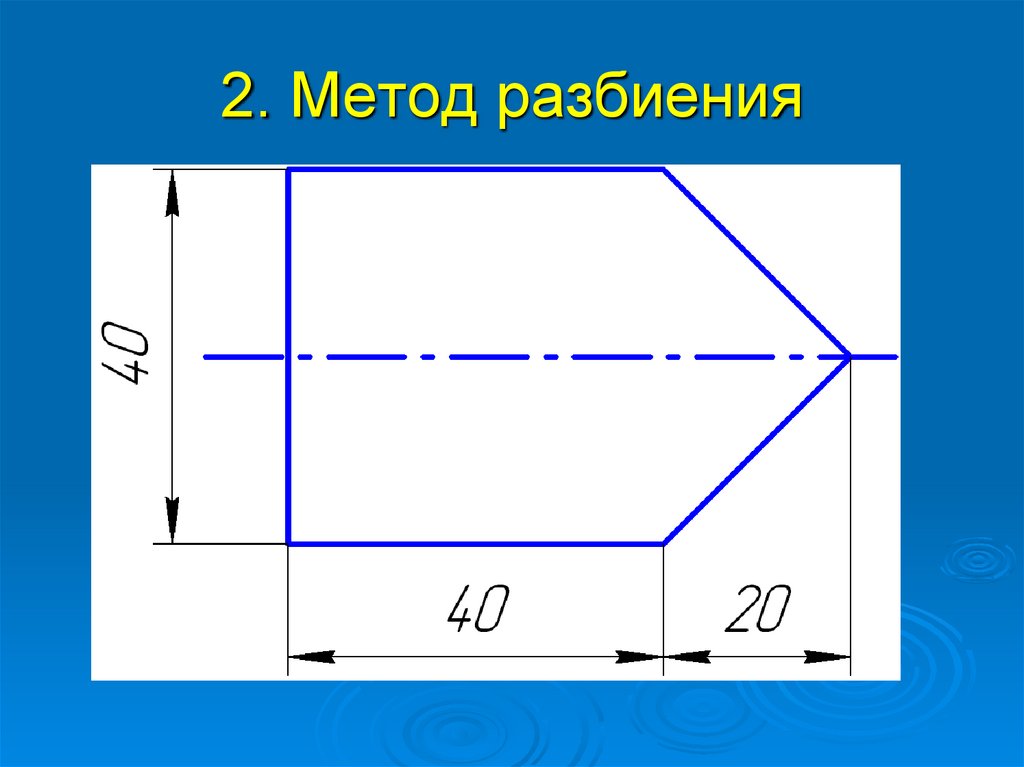
7. 2. Метод разбиения
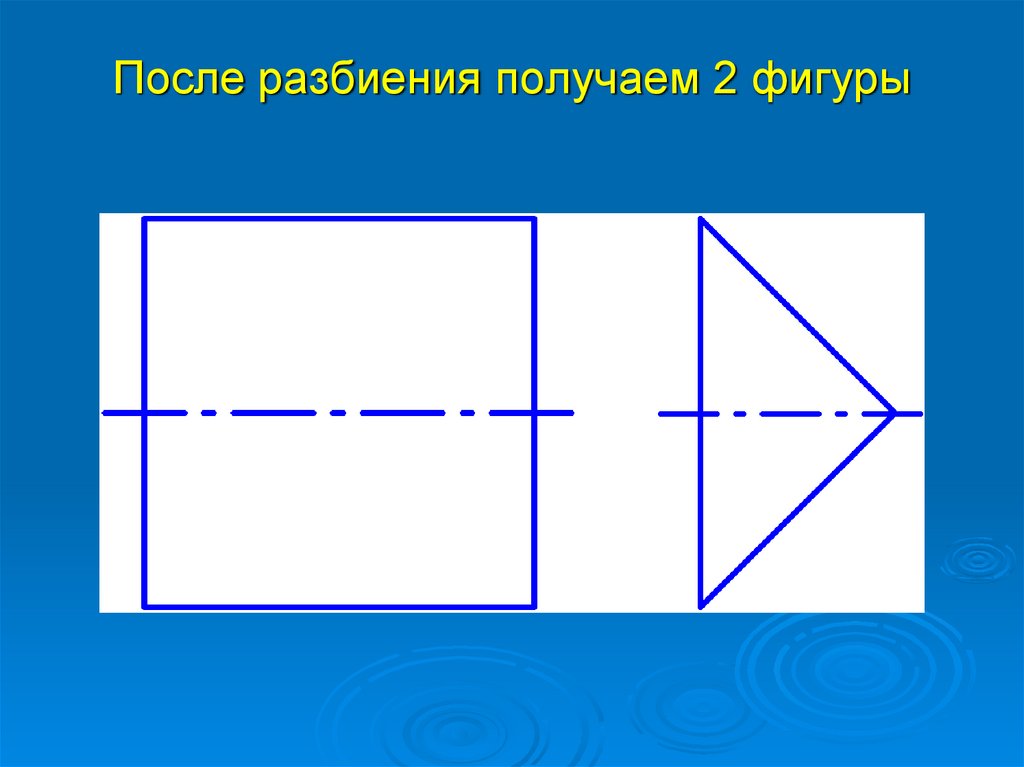
8.
После разбиения получаем 2 фигуры9.
A1 x1 A2 x2 ... An xnxc
A1 A2 ... An
Где А1- площадь первой фигуры;
А2- площадь второй фигуры;
Аn- площадь n-ой фигуры;
Х1- координата х центра тяжести первой фигуры;
Х2- координата х центра тяжести второй фигуры;
Х3- координата х центра тяжести n-ой фигуры;
n – число частей, на которое разбито тело.
10.
A1 y1 A2 y2 ... An ynyc
A1 A2 ... An
Где А1- площадь первой фигуры;
А2- площадь второй фигуры;
Аn- площадь n-ой фигуры;
y1- координата y центра тяжести первой
фигуры;
y2- координата y центра тяжести второй
фигуры;
y3- координата y центра тяжести n-ой фигуры;
n – число частей, на которое разбито тело.
11.
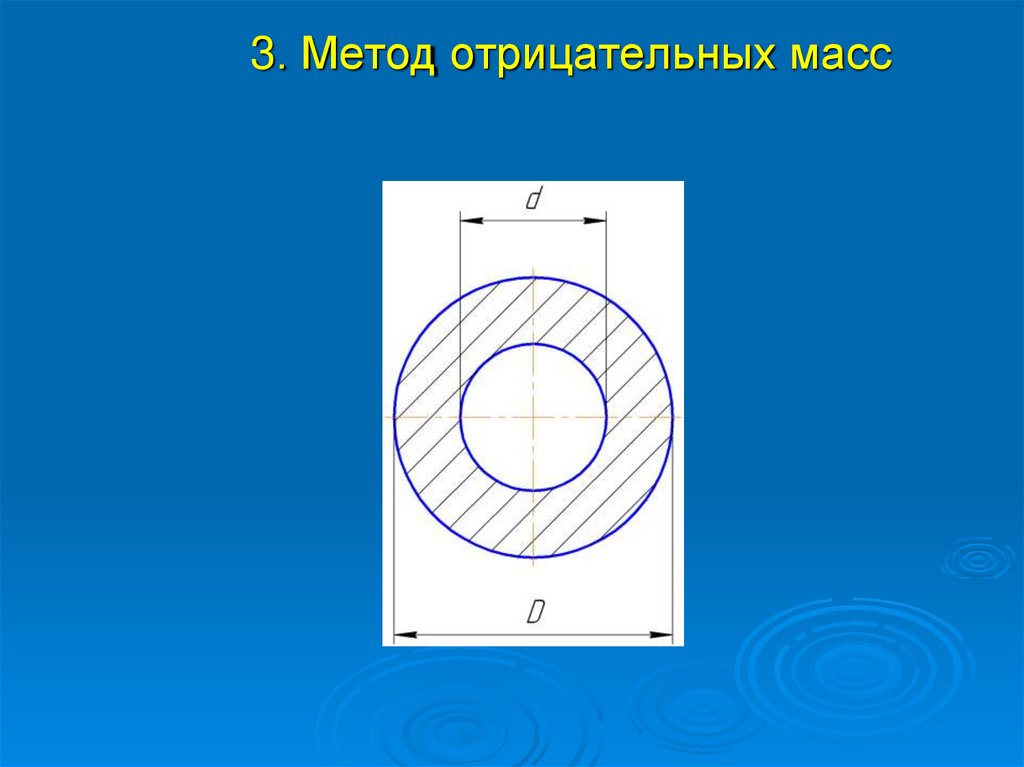
3. Метод отрицательных масс12.
A1 x1 A2 x2xc
A1 A2
Где А1- площадь первой фигуры;
А2- площадь второй фигуры;
Х1- координата х центра тяжести
первой фигуры;
Х2- координата х центра тяжести
второй фигуры;
13.
A1 y1 A2 y2yc
A1 A2
Где А1- площадь первой фигуры;
А2- площадь второй фигуры;
у1- координата у центра тяжести
первой фигуры;
у2- координата у центра тяжести
второй фигуры;
14. 3. Нахождение центра тяжести и площадей геометрических фигур, на которые может быть разделено тело.
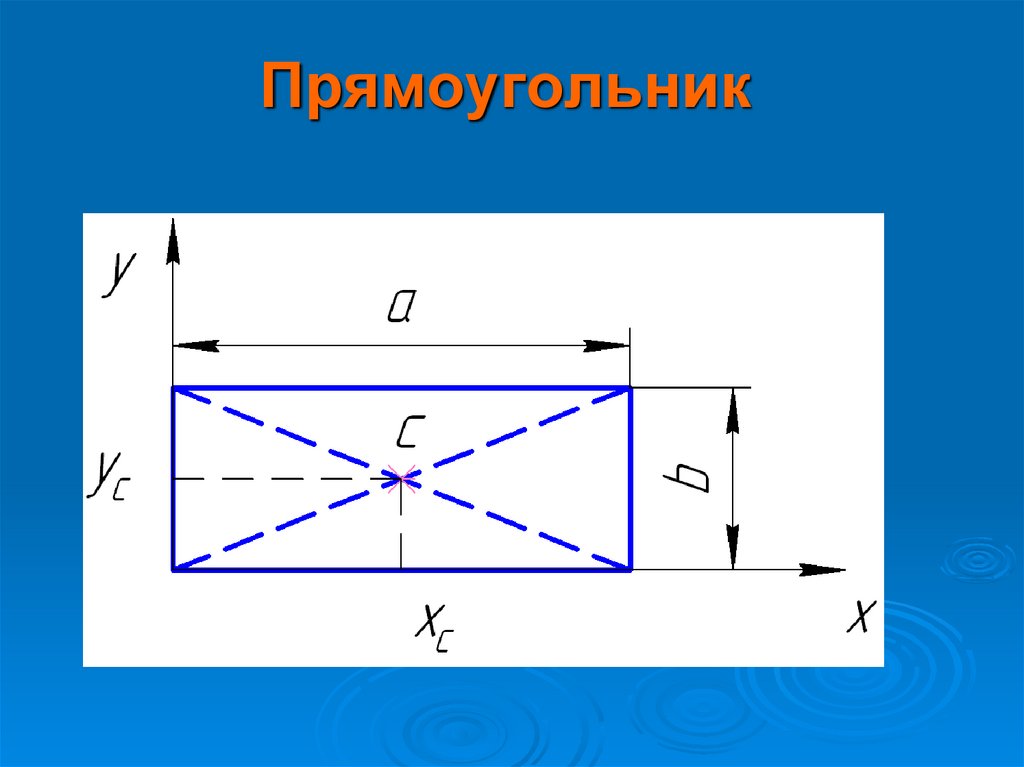
15. Прямоугольник
16.
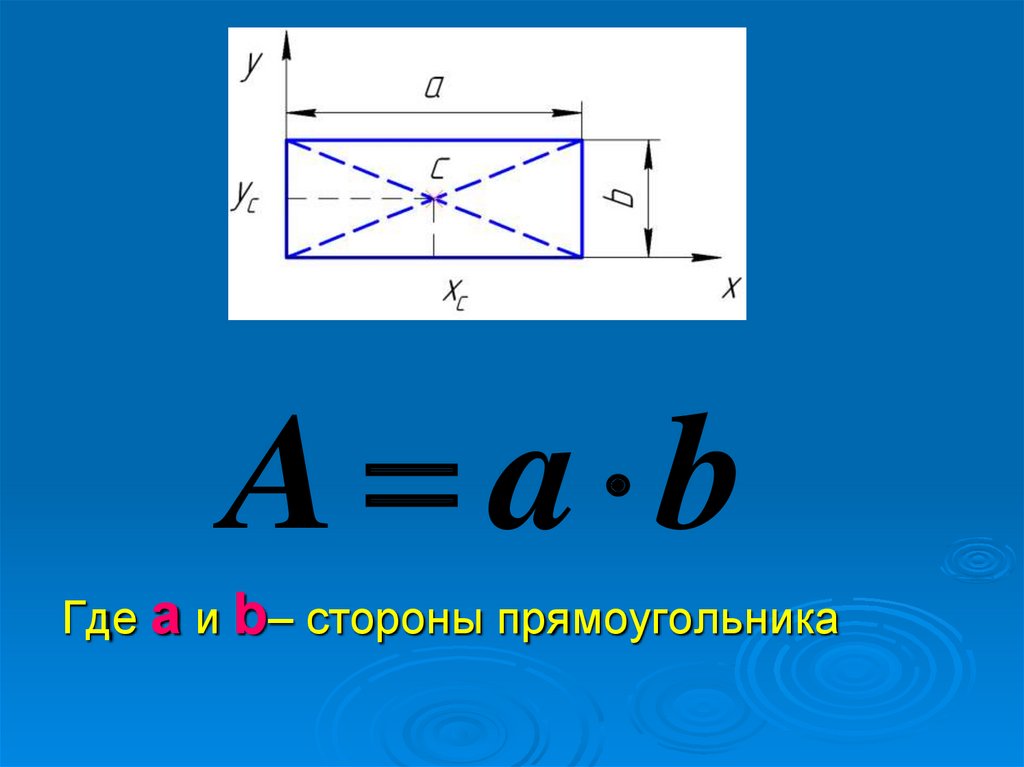
A a bГде а и b– стороны прямоугольника
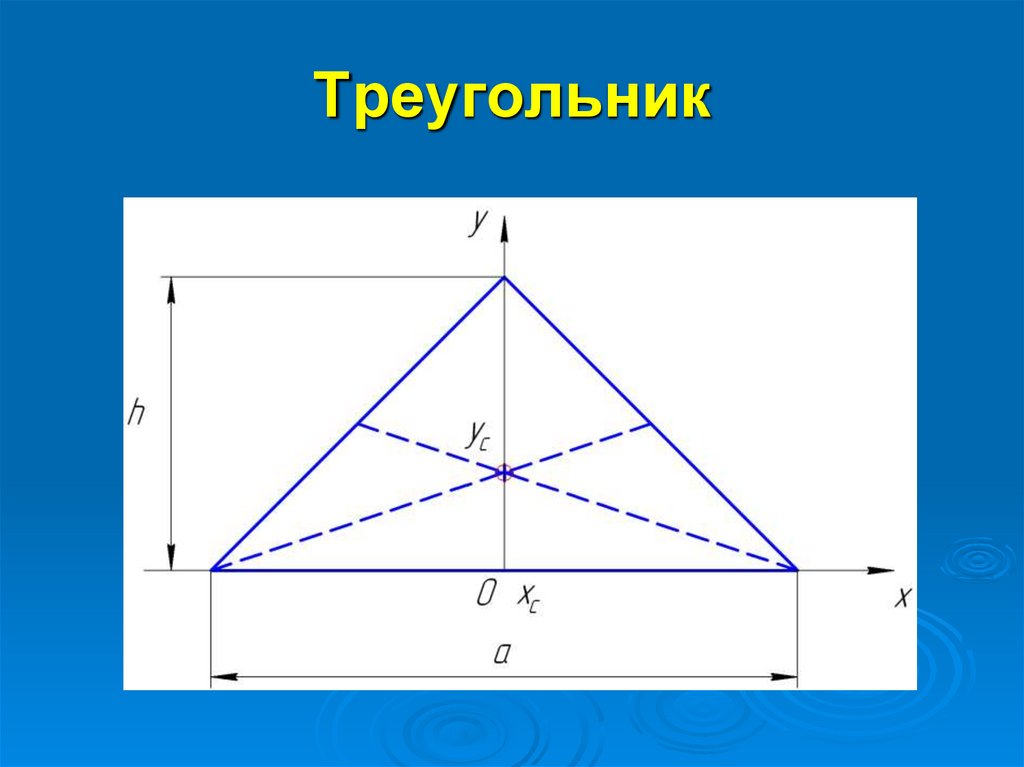
17. Треугольник
18.
1A h a
2
Где h – высота треугольника;
а – основание треугольника.
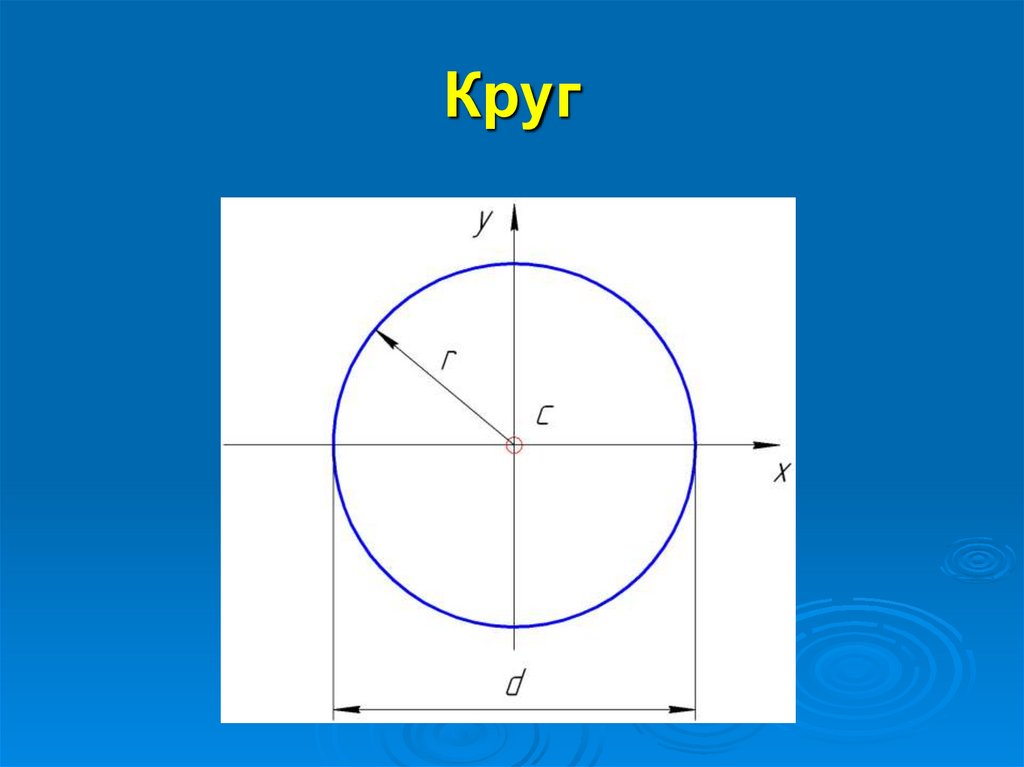
19. Круг
20.
A r2
d 2 d
A ( )
2
4
Где r – радиус круга;
d – диаметр круга;
2
21. 4. Нахождение центра тяжести стандартных прокатных профилей
Двутавр;Швеллер;
Уголок
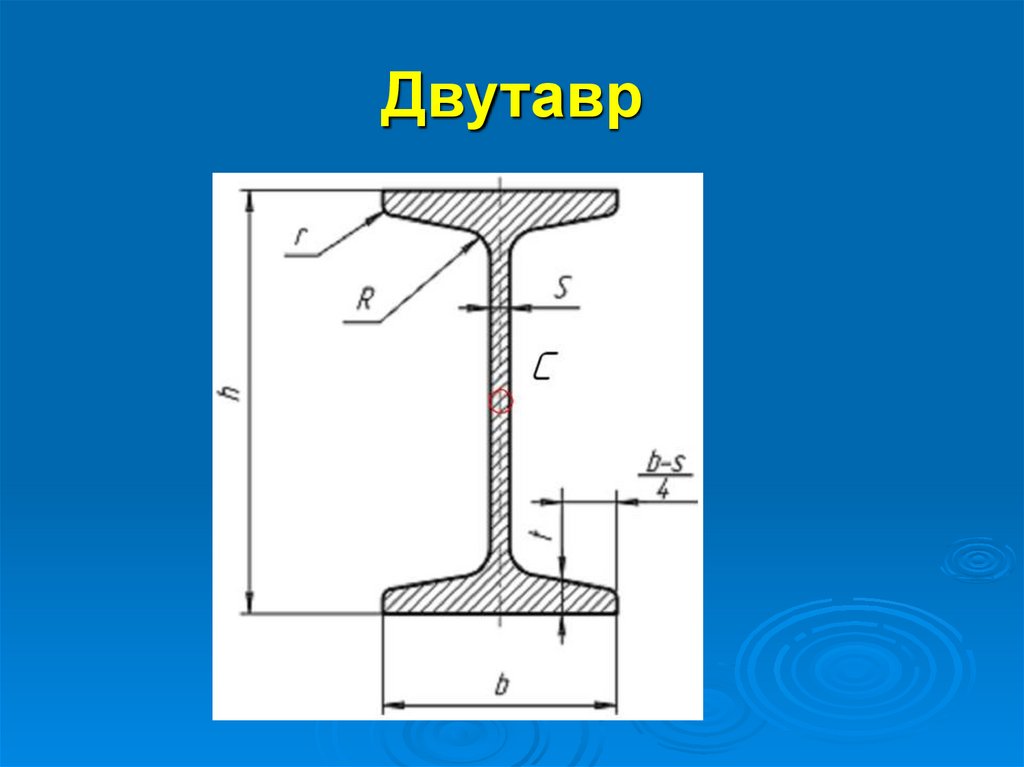
22. Двутавр
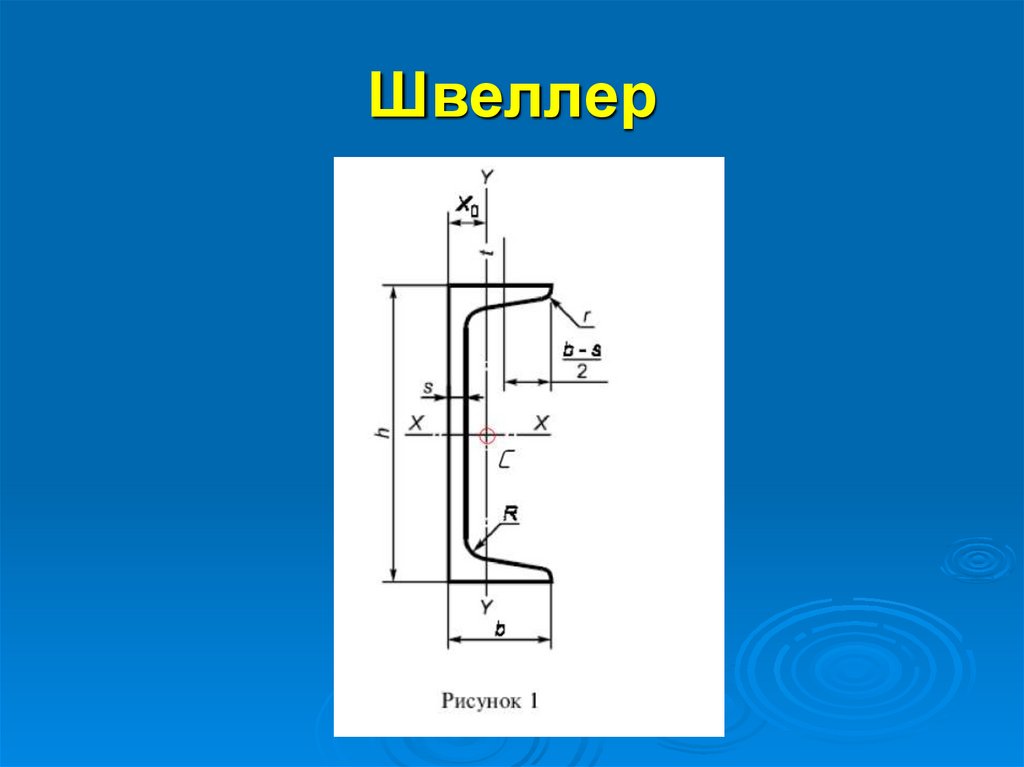
23. Швеллер
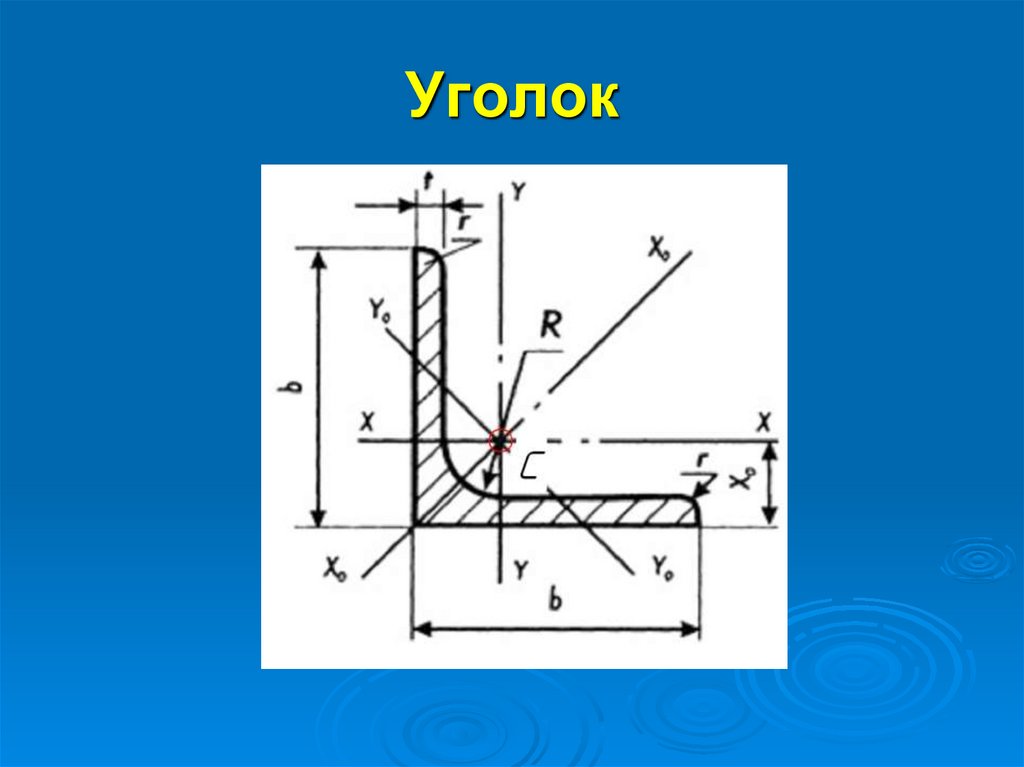
24. Уголок
25. 5. Нахождение центра тяжести объемных фигур
26.
V1 x1 V2 x2 ... Vn xnxc
V1 V2 ... Vn
Где V1- площадь первой фигуры;
V2- площадь второй фигуры;
Vn- площадь n-ой фигуры;
Х1- координата х центра тяжести первой
фигуры;
Х2- координата х центра тяжести второй
фигуры;
Х3- координата х центра тяжести n-ой фигуры;
n – число частей, на которое разбито тело.
27.
V1 y1 V2 y2 ... Vn ynyc
A1 A2 ... An
V1 z1 V2 z2 ... Vn zn
zc
V1 V2 ... Vn
28. Домашнее задание
--
Назвать простые объемные фигуры;
Написать формулу нахождения объема
и центра тяжести для этих фигур.















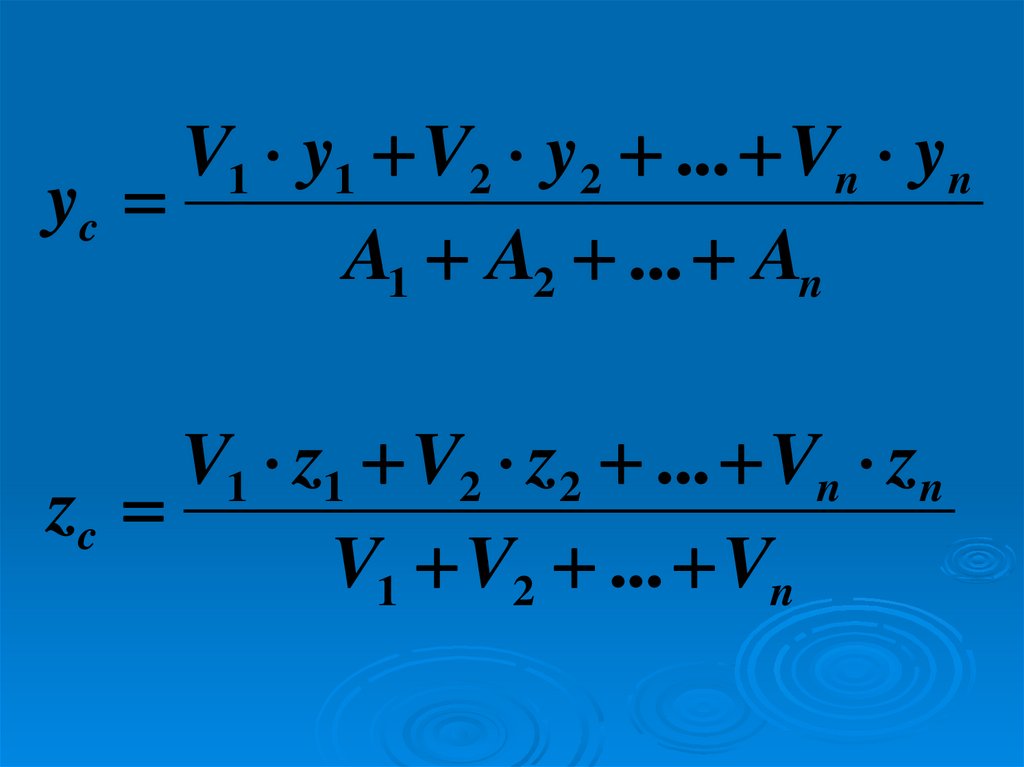

 physics
physics








