Similar presentations:
Лекция 09. Центр тяжести
1.
F , F ,..., F ,..., FF , F ,..., F ,..., F R , M
z
F1
A1
Fn
A2
F2
Ai
1
2
i
n
1
2
i
n
Rx
Ry
Rz
0;
0;
F 0.
n
F
i 1 ix
n
F
i 1 iy
n
i 1 iz
F 0;
i 1 ix
Fi n Fiy 0 ;
i 1
n
Fiz 0.
i
1
y
n
in 1 M x ( F i ) 0 ;
ni 1 M y ( F i ) 0 ;
i 1 Mz ( F i ) 0.
Mx
My
Mz
n
M x ( F i ) 0;
i 1
n
M y( F i ) 0;
i 1
n
M z ( F i ) 0.
i 1
n
An
O
x
ni 1 Fiz 0.
in 1 M x ( F i ) 0 ;
i 1 M y ( F i ) 0 ;
n
2.
A1CC
α
α
B
α
*
*
F1
R F1 F2 ;
R F1 F2 ;
AC BC F2 F1 ;
1
C1
A
F , F R ;
F2
2
* * *
* *
*
F1 , F2 R ; R F1 F2 ;
*
*
*
R F1 F2 F1 F2 R;
A1C1 BC1 F2* F1* F2 F1 ;
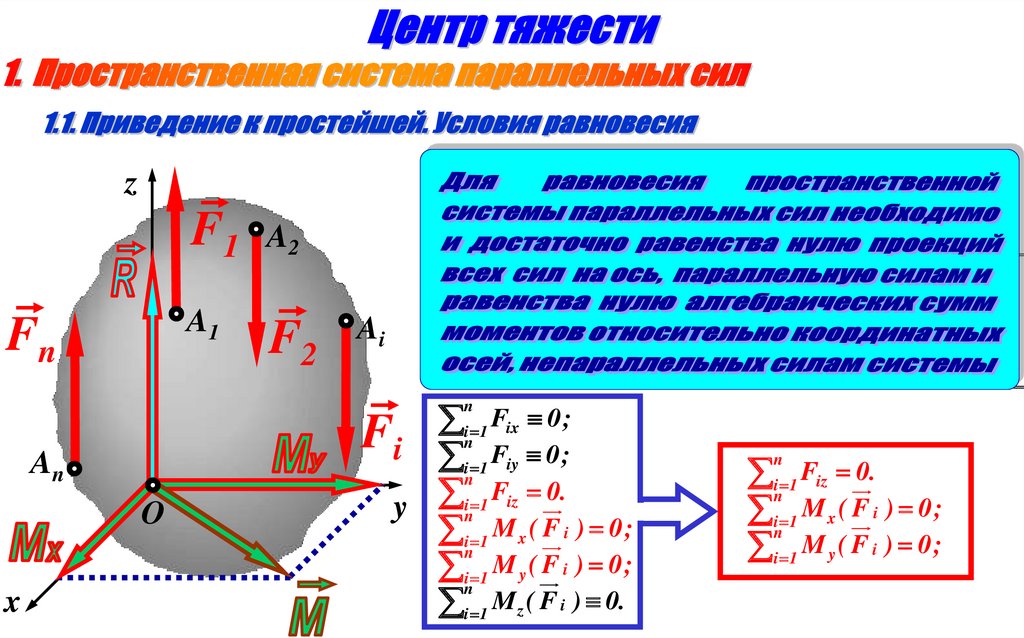
При повороте любой системы параллельных сил вокруг их
точек приложения на одинаковый угол равнодействующая
так же поворачивается вокруг своей точки приложения
на тот же угол.
На линии действия равнодействующей имеется точка,
вокруг которой она поворачивается при повороте
системы параллельных сил. Эта точка называется –
центр системы параллельных сил.
3.
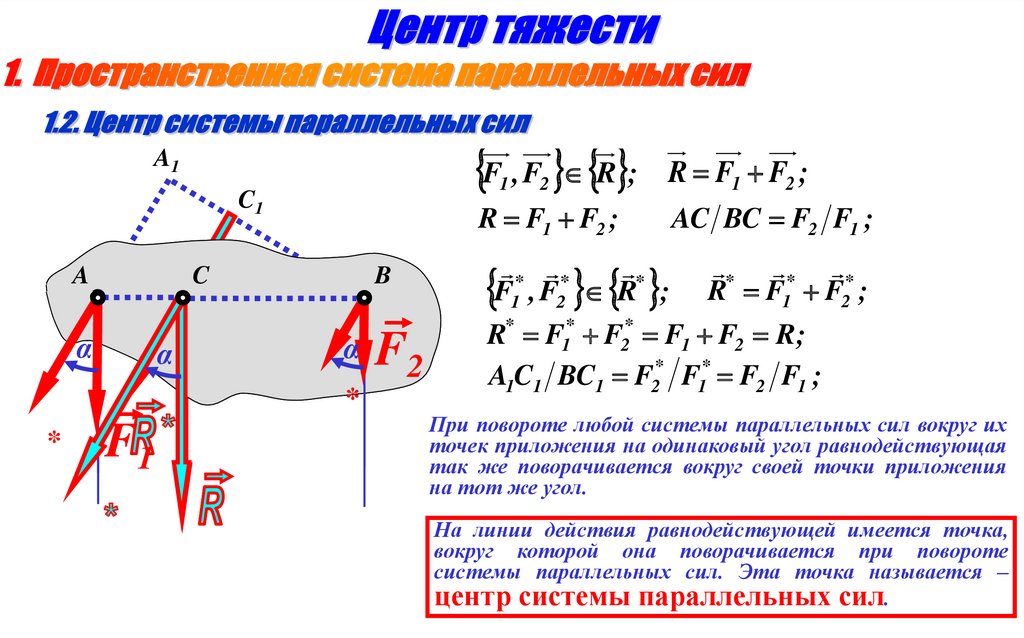
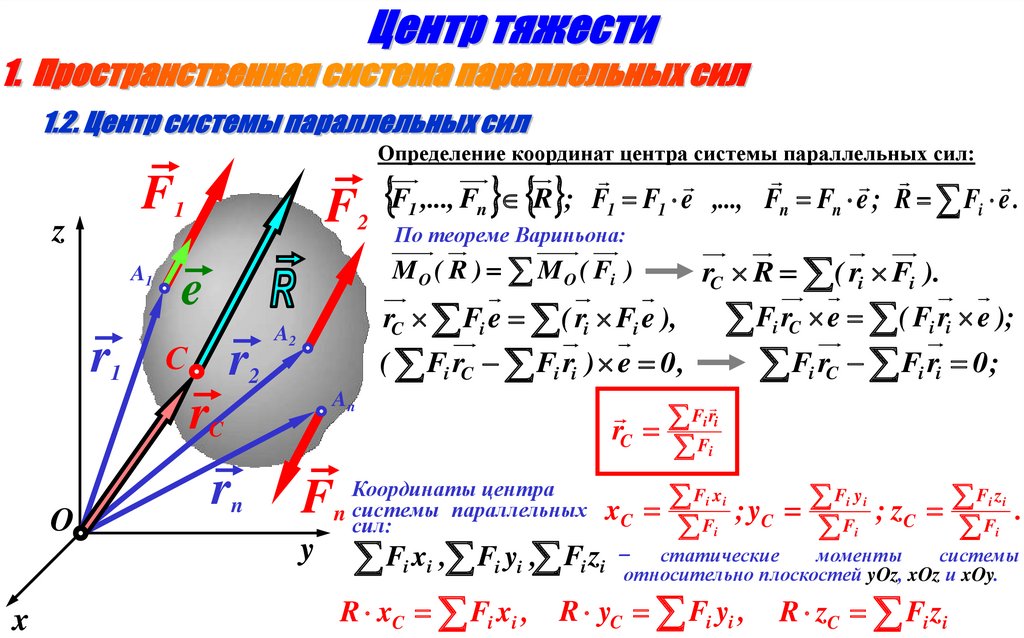
Определение координат центра системы параллельных сил:F2 По теореме Вариньона:
F1 ,..., Fn R ; F1 F1 e ,..., Fn Fn e ; R Fi e .
F1
z
A1
r1
M O ( R ) M O ( Fi )
e
С
r2
rC Fi e ( ri Fi e ),
A2
( Fi rC Fi ri ) e 0 ,
An
rC
O
x
rn
rC R ( ri Fi ).
Координаты центра
n системы параллельных
сил:
F
y
Fi rC e ( Fi ri e );
Fi rC Fi ri 0 ;
Fi r i
rC F
i
Fi x i
Fi z i
Fi y i
x C F ; yC F ; z C F .
i
i
i
статические
моменты
системы
Fi xi , Fi yi , Fi zi ̶относительно
плоскостей yOz, xOz и xOy.
R xC Fi xi , R yC Fi yi , R zC Fi zi
4.
ΔΔ
v
2
v
1
P2
Δ
P1
Δ
z
Pi
C
Δ
rC
Δ
v
n
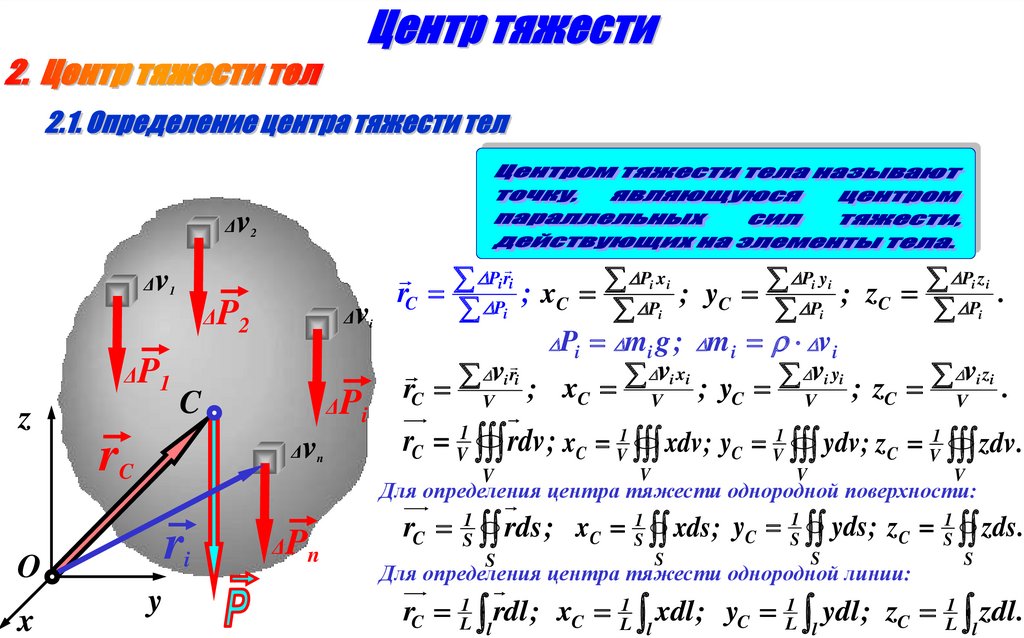
rC V1 rdv ; xC V1 xdv ; yC V1 ydv ; zC V1 zdv .
V
V
V
V
Для определения центра тяжести однородной поверхности:
ri
O
x
Pi r i
Pi z i
Pi x i
Pi yi
rC P ; xC P ; yC P ; zC P .
i
i
i
i
Δvi
Pi mi g ; m i v i
vi r i
vi xi
vi yi
vi zi
rC V ; xC V ; yC V ; zC V .
y
Pn
Δ
rC
1
S
1
x
xds ; yC
r
ds
;
C
S
S
S
1
S
yds; zC
S
Для определения центра тяжести однородной линии:
rC
1
rdl ;
L l
xC
1
xdl ;
L l
yC
1
ydl ;
L l
zC
1
S
zds.
S
1
zdl .
L l
5.
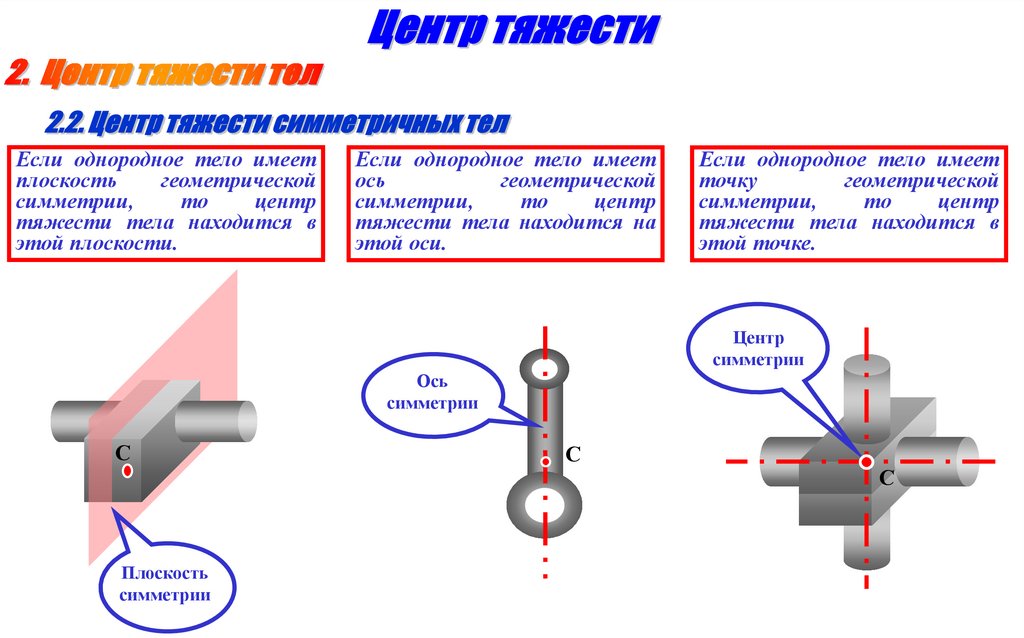
Если однородное тело имеетплоскость
геометрической
симметрии,
то
центр
тяжести тела находится в
этой плоскости.
Если однородное тело имеет
ось
геометрической
симметрии,
то
центр
тяжести тела находится на
этой оси.
Если однородное тело имеет
точку
геометрической
симметрии,
то
центр
тяжести тела находится в
этой точке.
Центр
симметрии
Ось
симметрии
С
Плоскость
симметрии
С
С
6.
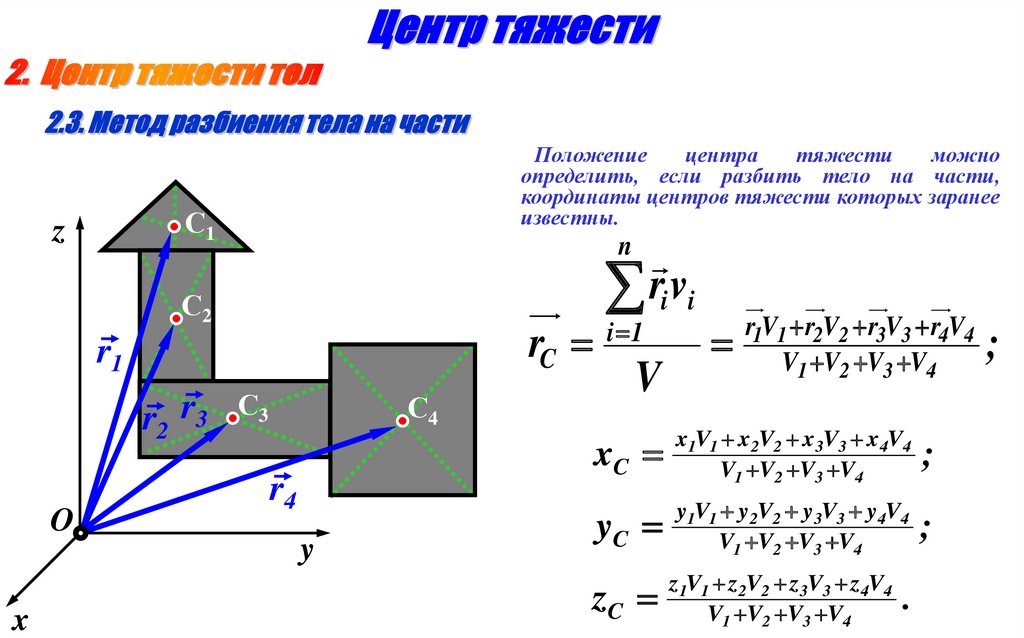
Положениецентра
тяжести
можно
определить, если разбить тело на части,
координаты центров тяжести которых заранее
известны.
С1
z
n
С2
rC
r1
С3
r
3
r2
O
x
С4
r4
y
ri vi
i 1
V
r1V1 r2V2 r3V3 r4V4
V1 V2 V3 V4
xC
x1V1 x 2V2 x 3V3 x4V4
V1 V2 V3 V4
;
yC
y1V1 y 2V2 y 3V3 y4V4
V1 V2 V3 V4
;
zC
z1V1 z 2V2 z 3V3 z 4V4
V1 V2 V3 V4
.
;
7.
Рассмотрим тело, имеющее пустые полости.Центр тяжести массы, которая могла бы занимать
полость обозначим как С2 , ее объем – V2 .
Центр тяжести полностью заполненного тела (без
полости) обозначим как С1 , его объем – V1 .
Центр тяжести тела с полостью (исходного)
обозначим как С, его объем – V .
z
С1
С
r
С2
1
r
r
O
x
V1 V V2 ;
r V r 2V2
r1 V1 ;
r
r1V1 r2V2
V1 V2
xC ( x1V1 x 2V2 ) ( V1 V2 ) ;
2
y
yC ( y1V1 y 2V2 ) ( V1 V2 ) ;
zC ( z1V1 z 2V2 ) ( V1 V2 ) .
.
8.
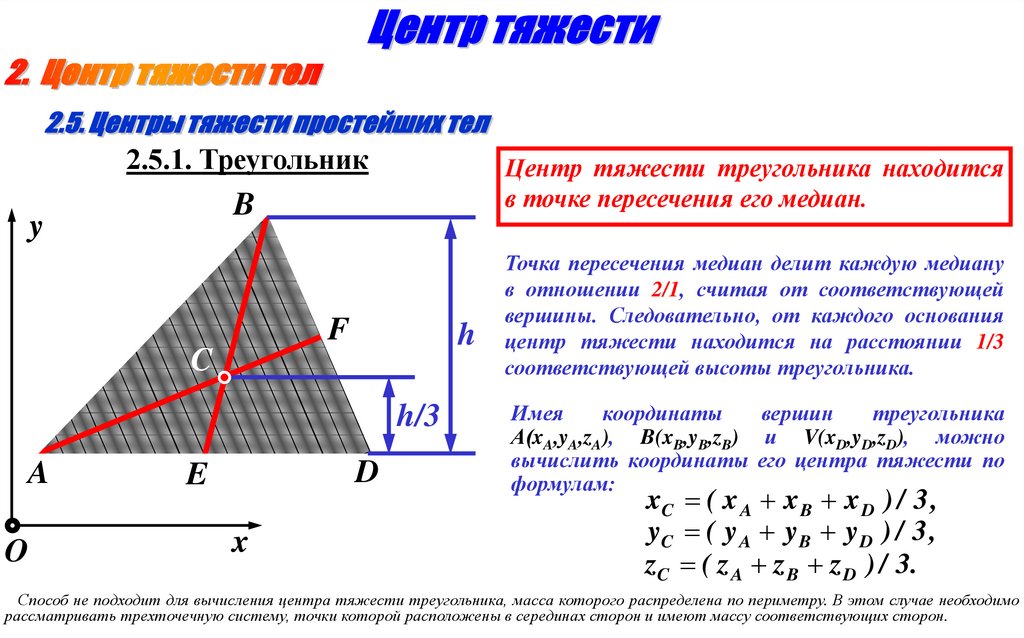
2.5.1. ТреугольникЦентр тяжести треугольника находится
в точке пересечения его медиан.
B
y
F
h
C
h/3
A
O
D
E
x
Точка пересечения медиан делит каждую медиану
в отношении 2/1, считая от соответствующей
вершины. Следовательно, от каждого основания
центр тяжести находится на расстоянии 1/3
соответствующей высоты треугольника.
Имея
координаты
вершин
треугольника
А(xA,yA,zA), B(xB,yB,zB) и V(xD,yD,zD), можно
вычислить координаты его центра тяжести по
формулам:
xC ( x A x B x D ) / 3 ,
yC ( y A y B y D ) / 3 ,
zC ( z A z B z D ) / 3.
Способ не подходит для вычисления центра тяжести треугольника, масса которого распределена по периметру. В этом случае необходимо
рассматривать трехточечную систему, точки которой расположены в серединах сторон и имеют массу соответствующих сторон.
9.
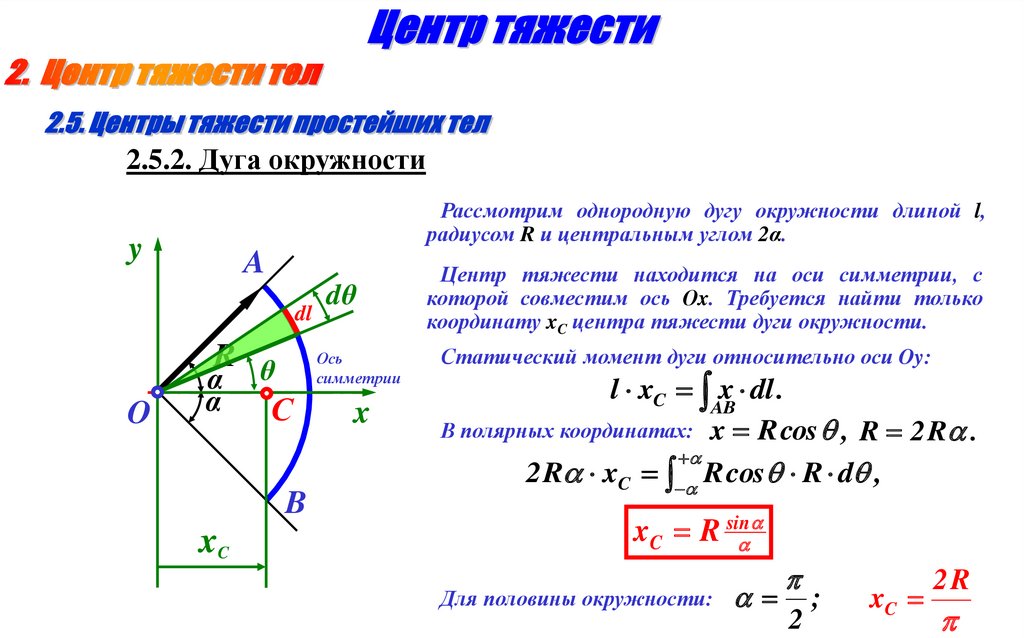
2.5.2. Дуга окружностиРассмотрим однородную дугу окружности длиной l,
радиусом R и центральным углом 2α.
y
A
dl
O
R θ
α
α
С
B
xC
dθ
Ось
симметрии
x
Центр тяжести находится на оси симметрии, с
которой совместим ось Оx. Требуется найти только
координату xC центра тяжести дуги окружности.
Статический момент дуги относительно оси Oy:
l xC x dl .
AB
В полярных координатах: x R cos , R 2 R .
2 R xC R cos R d ,
xC R sin
Для половины окружности:
2
;
xC
2R
10.
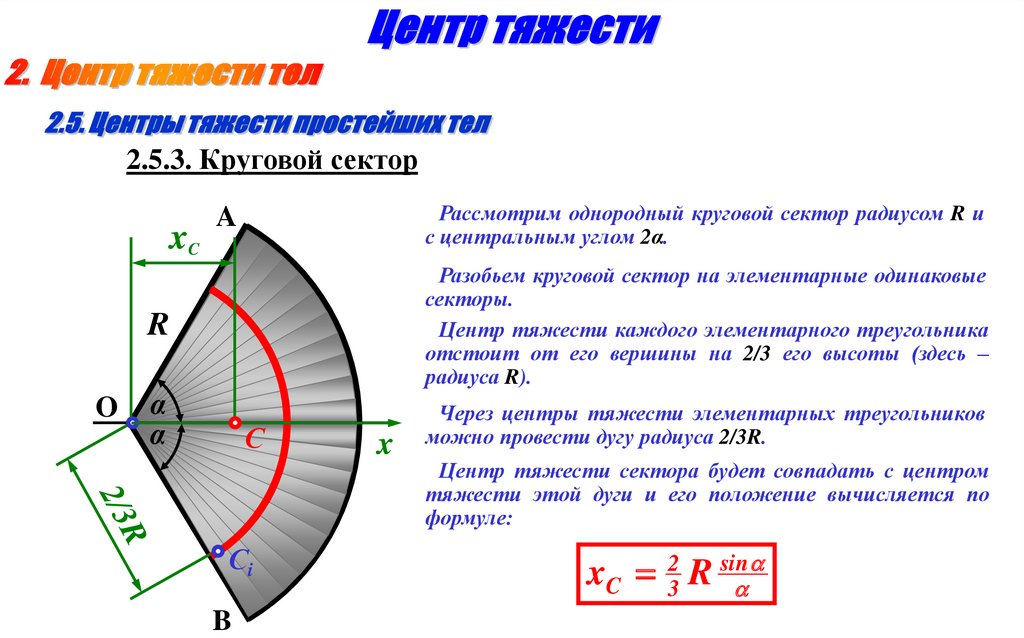
2.5.3. Круговой секторxC
Рассмотрим однородный круговой сектор радиусом R и
с центральным углом 2α.
A
Разобьем круговой сектор на элементарные одинаковые
секторы.
Центр тяжести каждого элементарного треугольника
отстоит от его вершины на 2/3 его высоты (здесь –
радиуса R).
R
O
α
α
С
Сi
B
x
Через центры тяжести элементарных треугольников
можно провести дугу радиуса 2/3R.
Центр тяжести сектора будет совпадать с центром
тяжести этой дуги и его положение вычисляется по
формуле:
xC R
2
3
sin
11.
2.5.4. Объем конусаО
x
y
h
z
σ*
Определим центр тяжести конуса, имеющего ось
симметрии АО. Высота конуса – h, площадь основания
конуса – σ, объем конуса – V.
Центр тяжести конуса лежит на оси симметрии, с
которой совмещена ось Оz .
zC
1
V
z dV ;
V
dz
dV * dz ,
А
z
где σ* – площадь сечения конуса с
координатой z .
2
* z
dV 2 z dz ;
2,
h
h
h
2
3
1
h zC z 2 z dz ,
zC 4 h
3
h
0
2
С
V h.
1
3
12.
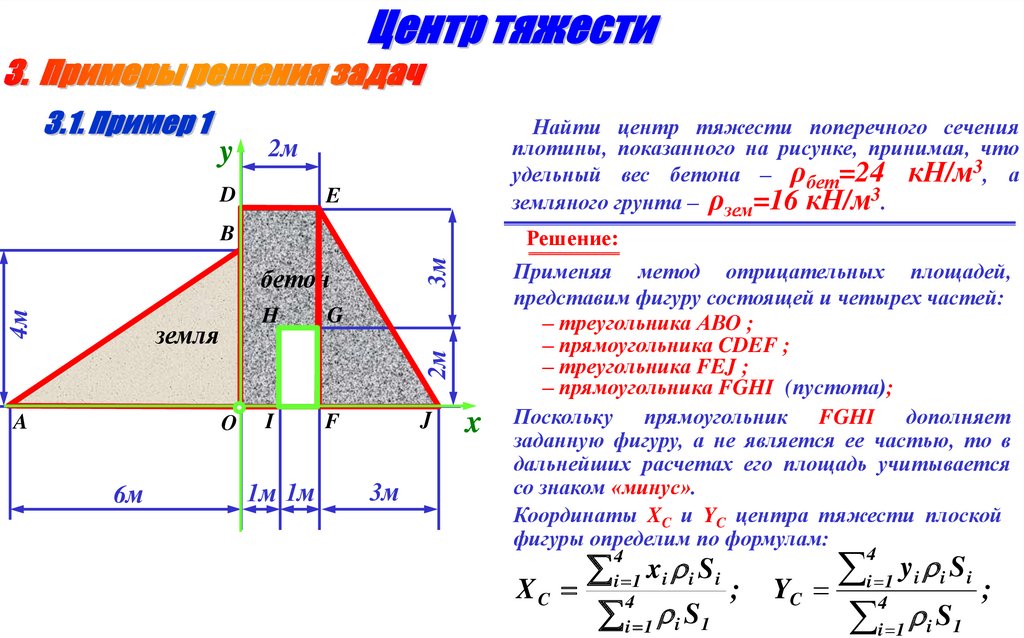
yНайти центр тяжести поперечного сечения
плотины, показанного на рисунке, принимая, что
удельный вес бетона – ρбет=24 кН/м3, а
земляного грунта – ρзем=16 кН/м3.
2м
D
E
Решение:
3м
B
4м
бетон
G
I
F
2м
земля
H
A
O
6м
1м 1м
J
3м
x
Применяя метод отрицательных площадей,
представим фигуру состоящей и четырех частей:
– треугольника АВO ;
– прямоугольника CDEF ;
– треугольника FEJ ;
– прямоугольника FGHI (пустота);
Поскольку прямоугольник FGHI дополняет
заданную фигуру, а не является ее частью, то в
дальнейших расчетах его площадь учитывается
со знаком «минус».
Координаты XC и YC центра тяжести плоской
фигуры определим по формулам:
y S
x S
i 1 i i i
;
XC
; YC
4
S
i 1 i S 1
4
i 1 i i i
4
i 1 i 1
4
13.
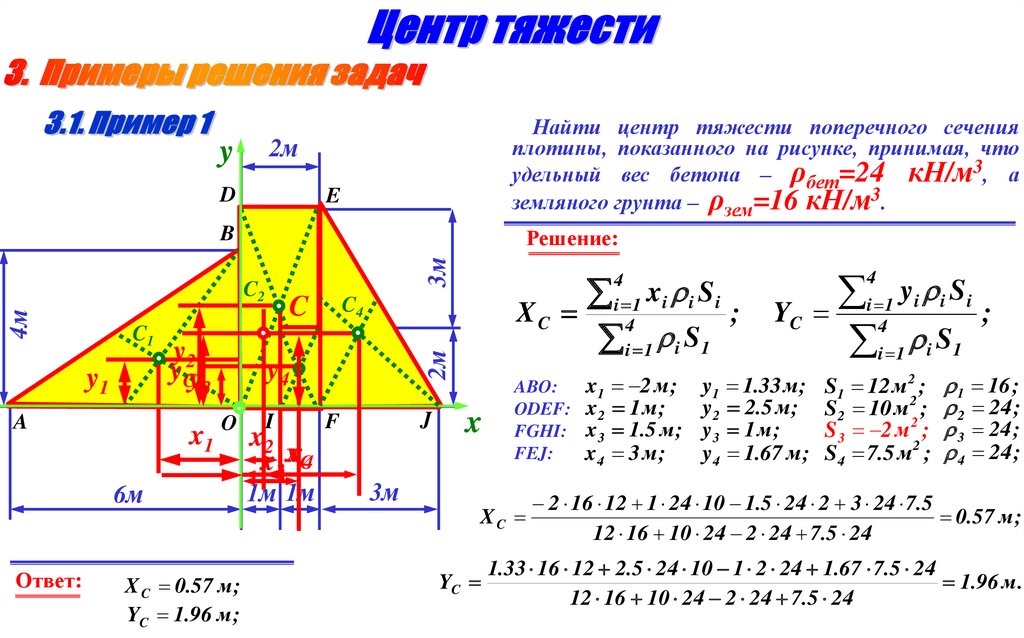
Найти центр тяжести поперечного сеченияплотины, показанного на рисунке, принимая, что
удельный вес бетона – ρбет=24 кН/м3, а
земляного грунта – ρзем=16 кН/м3.
2м
y
D
E
Решение:
3м
B
C бетон
H
C1 земля
y2
yCy
y1
A
3
x1
O
6м
Ответ:
X C 0.57 м ;
YC 1.96 м ;
C
y4
C3
I
F
x2
x3xxC4
1м 1м
y S
x S
i 1 i i i
;
XC
; YC
4
S
i 1 i S 1
GC4
2м
4м
2
4
i 1 i i i
4
i 1 i 1
J
3м
x
ABO:
ODEF:
FGHI:
FEJ:
XC
YC
x1 2 м ;
x2 1 м ;
x 3 1.5 м ;
x4 3 м ;
y1 1.33 м ;
y2 2.5 м ;
y3 1 м ;
y4 1.67 м ;
4
S1 12 м2 ;
S 2 10 м 2 ;
S 3 2 м 2 ;
S4 7.5 м2 ;
1 16 ;
2 24 ;
3 24 ;
4 24 ;
2 16 12 1 24 10 1.5 24 2 3 24 7.5
0.57 м ;
12 16 10 24 2 24 7.5 24
1.33 16 12 2.5 24 10 1 2 24 1.67 7.5 24
1.96 м .
12 16 10 24 2 24 7.5 24
14.
yE
D
Дан квадрат ABDE, сторона которого равна а.
Найти внутри него такую точку С, чтобы она
была центром тяжести площади, которая
получится, если из квадрата вырезать
равнобедренный треугольник АСВ.
Решение:
C
xC 0 ; y C h .
ABDE: x1 0 ; y1 a 2 ;
C1
ABC:
y1
h
A
y2
C2
B
x
a
S1 a ;
x 2 0 ; y2 h 3 ; S 2 a h 2 ;
2
2
a
2
a
h 3 a h 2
y1 S 1 y 2 S 2
;
yC
; h
2
a a h 2
S1 S 2
2
2
2 h 6 ah 3a 0 ;
h1 2.365a ;
h2 0.635a ;
Ответ:
h 0.635a
15.
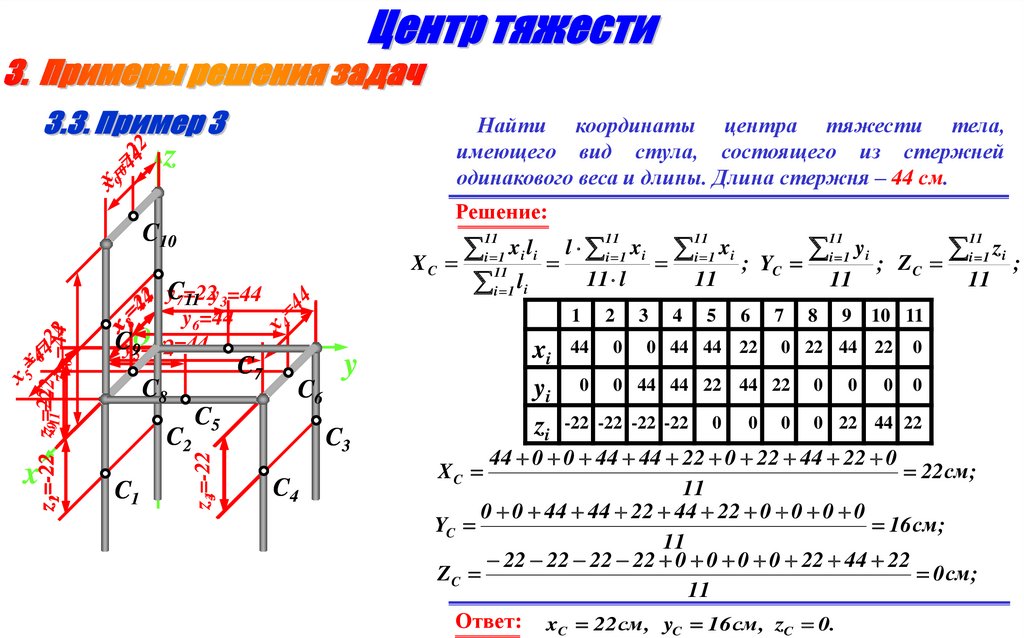
Найти координаты центра тяжести тела,имеющего вид стула, состоящего из стержней
одинакового веса и длины. Длина стержня – 44 см.
z
Решение:
x
XC
l
11
i 1 i i
11
i 1 i
xl
yC7=22
11 y3=44
y6=44
Cy9O
y4=44
5=22
C7
C8
C2
C1
C5
z43=-22
z12=-22 zz911=22
=22
z10=44
C10
l i 1 xi
11 l
11
1
C6
y
C3
C4
xi
yi
zi
44
0
2
0
3
11
i 1
xi
11
4
5
; YC
6
0 44 44 22
7
0
0
yi
11
9
z
;
; ZC
11
i 1 i
11
10 11
0 22 44 22
0 44 44 22 44 22
-22 -22 -22 -22
8
11
i 1
0
0
0
0
0
0
0 22 44 22
44 0 0 44 44 22 0 22 44 22 0
XC
22см ;
11
0 0 44 44 22 44 22 0 0 0 0
YC
16 см ;
11
22 22 22 22 0 0 0 0 22 44 22
ZC
0 см ;
11
Ответ: xC 22см , yC 16 см , zC 0.
16.
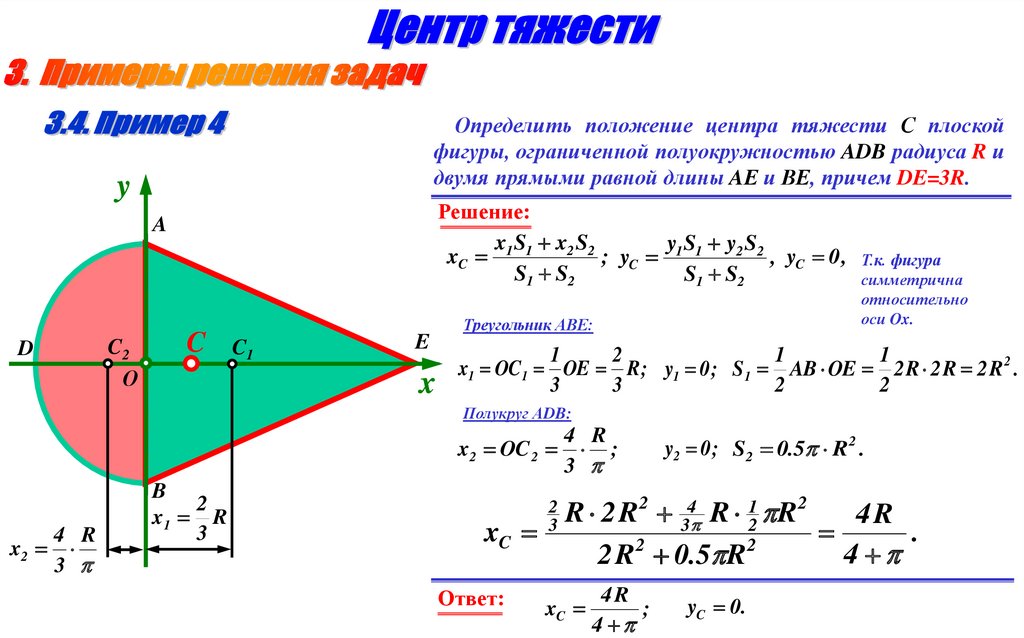
Определить положение центра тяжести С плоскойфигуры, ограниченной полуокружностью ADB радиуса R и
двумя прямыми равной длины AЕ и ВЕ, причем DE=3R.
y
Решение:
x1 S1 x2 S2
y1 S1 y2 S2
xC
; yC
, yC 0 ,
S1 S2
S1 S2
A
C2
О
D
C
C1
E
x
Треугольник АВЕ:
Т.к. фигура
симметрична
относительно
оси Ox.
1
2
1
1
x1 OC 1 OE R ; y1 0 ; S1 AB OE 2 R 2 R 2 R 2 .
2
2
3
3
Полукруг АDB:
4 R
x2 OC 2 ;
3
x2
4 R
3
B
2
x1 R
3
y2 0 ; S2 0.5 R 2 .
R 2 R R R
4R
xC
.
2
4
2 R 0.5 R
2
3
Ответ:
2
4R
xC
;
4
4
3
yC 0.
1
2
2
2
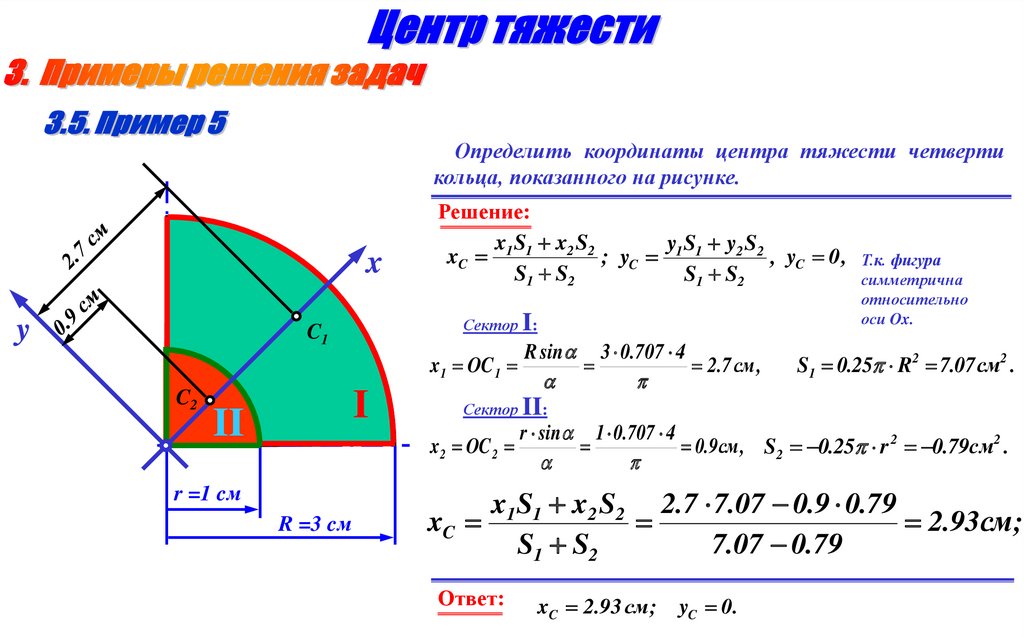
17.
Определить координаты центра тяжести четвертикольца, показанного на рисунке.
x
y
Сектор I:
C1
C2
I
II
r =1 cм
R =3 cм
Решение:
x1 S1 x2 S2
y1 S1 y2 S2
xC
; yC
, yC 0 ,
S1 S2
S1 S2
R sin 3 0.707 4
x1 OC 1
2.7 см ,
Т.к. фигура
симметрична
относительно
оси Ox.
S1 0.25 R2 7.07 см2 .
Сектор II:
r sin 1 0.707 4
x 2 OC 2
0.9см , S2 0.25 r 2 0.79см2 .
x1 S1 x2 S2 2.7 7.07 0.9 0.79
xC
2.93см ;
S1 S2
7.07 0.79
Ответ:
xC 2.93 см ;
yC 0.



 physics
physics