Центр системы параллельных сил. Центр тяжести. Тема 4

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
Кафедра строительной механики
Теоретическая механика
Тема 2
Статика. Центр тяжести.
Юлина Анна Олеговна
1

2.

Лекция № 4
Тема 4. Центр системы параллельных сил.
Центр тяжести.
УЧЕБНЫЕ ВОПРОСЫ
4.1. Центр системы параллельных сил
4.2. Центр тяжести
4.3. Методы определения центра тяжести

3.

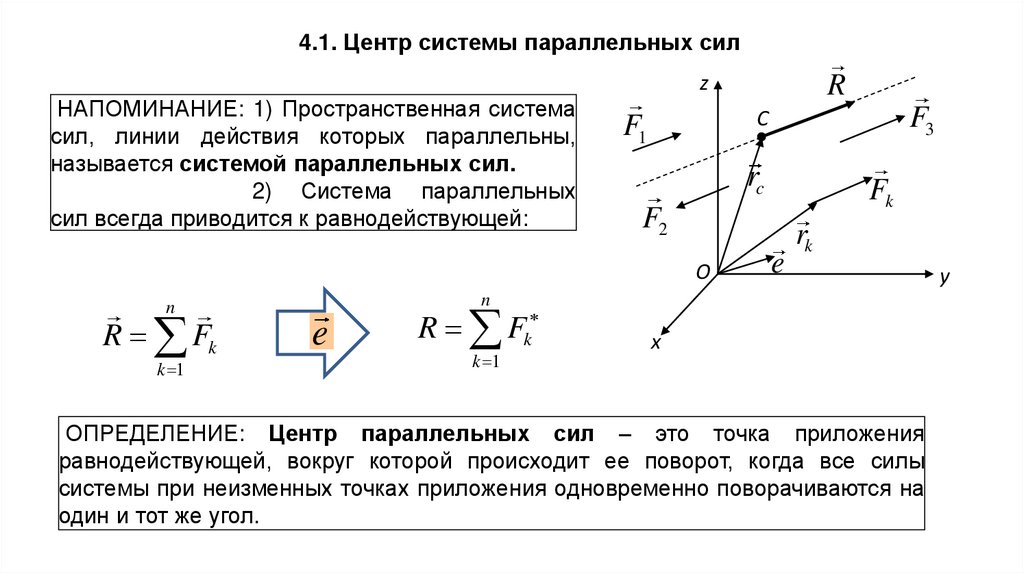
4.1. Центр системы параллельных сил
НАПОМИНАНИЕ: 1) Пространственная система
сил, линии действия которых параллельны,
называется системой параллельных сил.
2) Система параллельных
сил всегда приводится к равнодействующей:
z
rc
Fk
F2
e
rk
n
n
k 1
F3
C
F1
O
R Fk
R
e
R Fk
k 1
x
ОПРЕДЕЛЕНИЕ: Центр параллельных сил – это точка приложения
равнодействующей, вокруг которой происходит ее поворот, когда все силы
системы при неизменных точках приложения одновременно поворачиваются на
один и тот же угол.
y

4.

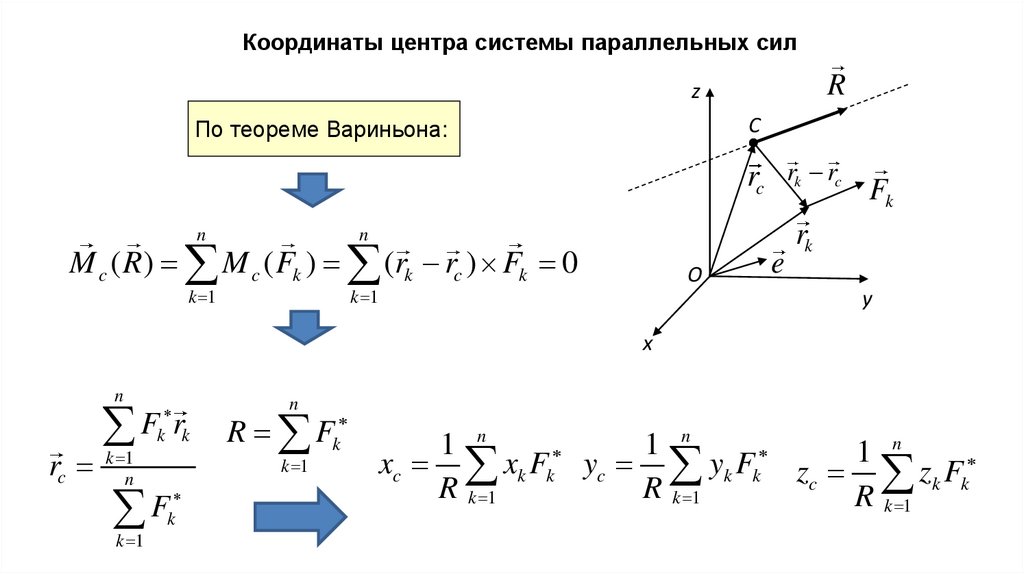
Координаты центра системы параллельных сил
R
z
C
По теореме Вариньона:
n
n
M c ( R) M c ( Fk ) (rk rc ) Fk 0
k 1
O
k 1
rc rk rc F
k
rk
e
y
x
n
F r
rc k n1
k k
F
k
k 1
n
R Fk
k 1
n
1 n
1 n
1
xc xk Fk yc yk Fk z z F
c
k k
R k 1
R k 1
R k 1

5.

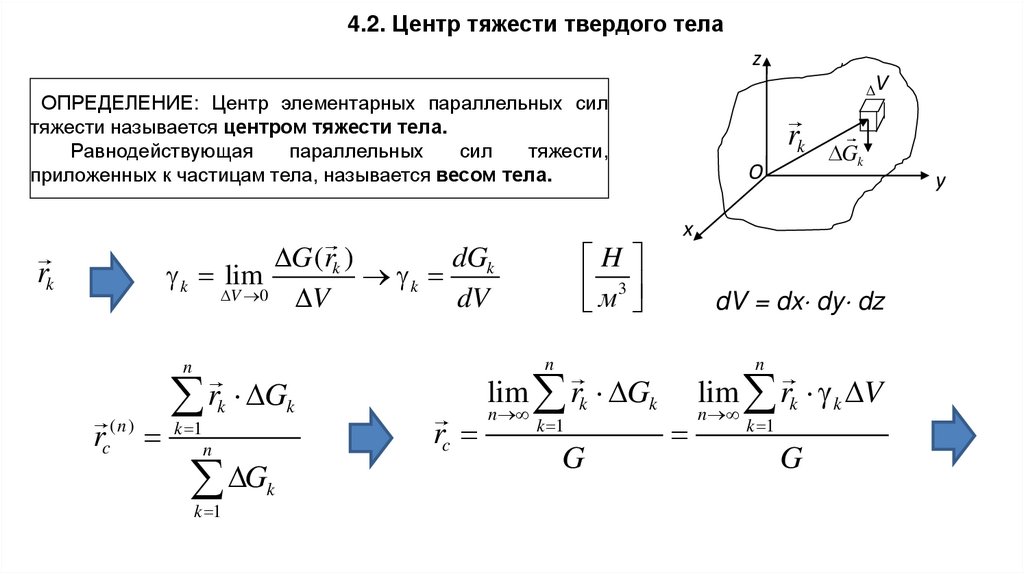
4.2. Центр тяжести твердого тела
z
V
ОПРЕДЕЛЕНИЕ: Центр элементарных параллельных сил
тяжести называется центром тяжести тела.
Равнодействующая
параллельных
сил
тяжести,
приложенных к частицам тела, называется весом тела.
G (rk )
dGk
k lim
k
V 0
V
dV
rk
(n)
c
r
k
k 1
n
Gk
k 1
k
O
rc
lim rk Gk
n
k 1
G
Gk
y
x
dV = dx dy dz
n
n
r G
H
м3
rk
n
lim rk k V
n
k 1
G

6.

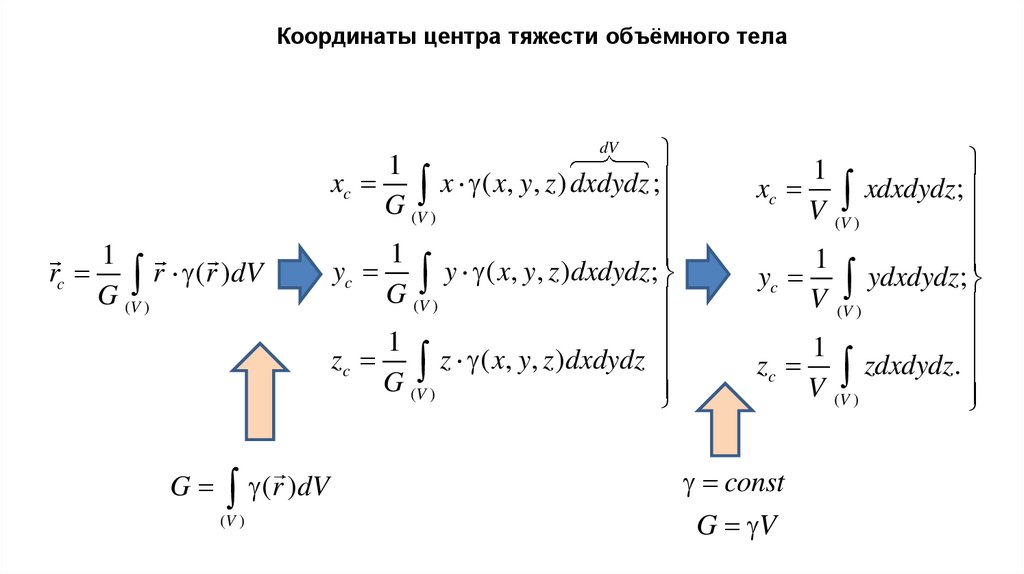
Координаты центра тяжести объёмного тела
rc
1
r (r )dV
G (V )
G (r )dV
(V )
dV
1
xc x ( x, y, z ) dxdydz ;
G (V )
1
yc y ( x, y, z )dxdydz;
G (V )
1
zc z ( x, y, z )dxdydz
G (V )
1
xc xdxdydz;
V (V )
1
yc ydxdydz;
V (V )
1
zc zdxdydz.
V (V )
const
G V

7.

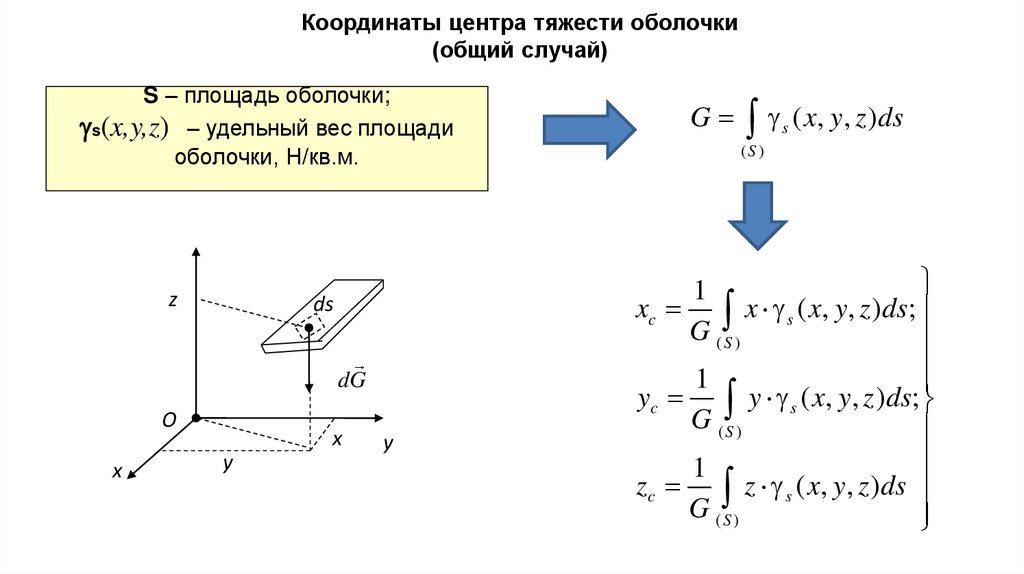
Координаты центра тяжести оболочки
(общий случай)
S – площадь оболочки;
s(x,y,z) – удельный вес площади
оболочки, Н/кв.м.
z
ds
dG
O
x
x
y
y
G s ( x, y, z )ds
(S )
1
xc x s ( x, y, z )ds;
G (S )
1
yc y s ( x, y, z )ds;
G (S )
1
zc z s ( x, y, z )ds
G (S )

8.

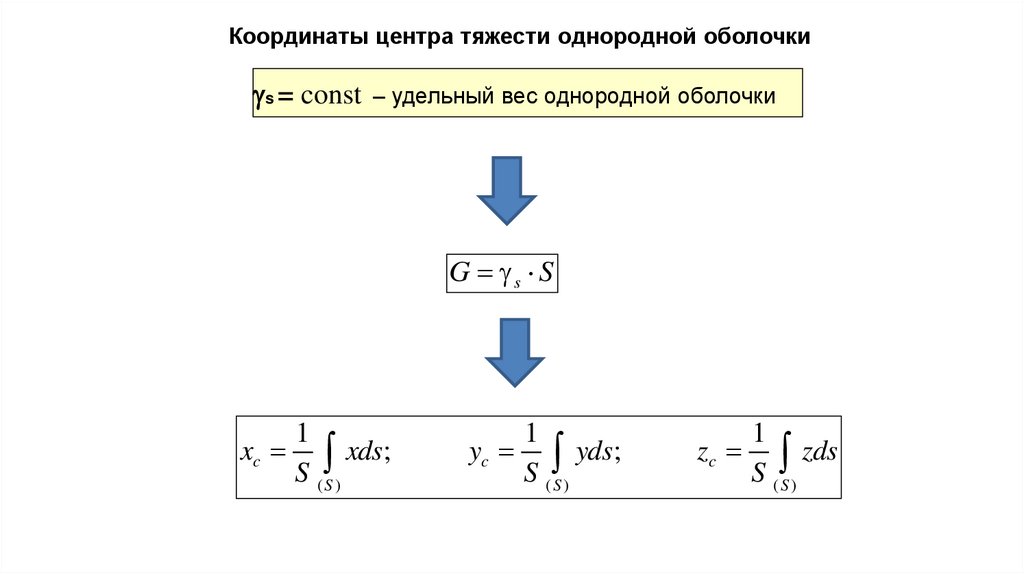
Координаты центра тяжести однородной оболочки
s = const – удельный вес однородной оболочки
G s S
xc
1
xds;
S (S )
yc
1
yds;
S (S )
zc
1
zds
S (S )

9.

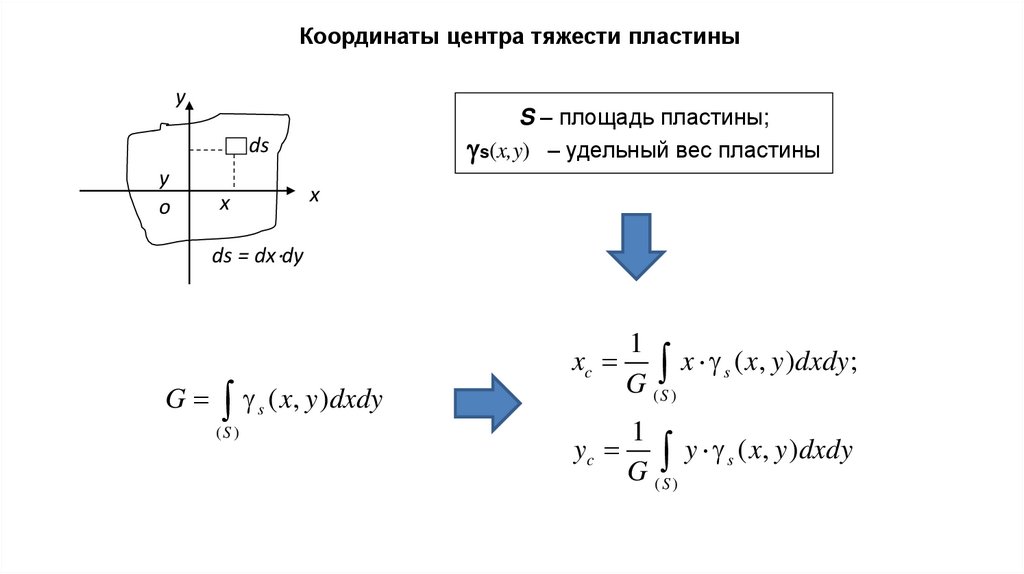
Координаты центра тяжести пластины
y
S – площадь пластины;
s(x,y) – удельный вес пластины
ds
y
o
x
x
ds = dx dy
G s ( x, y )dxdy
(S )
xc
1
x s ( x, y )dxdy;
G (S )
yc
1
y s ( x, y )dxdy
G (S )

10.

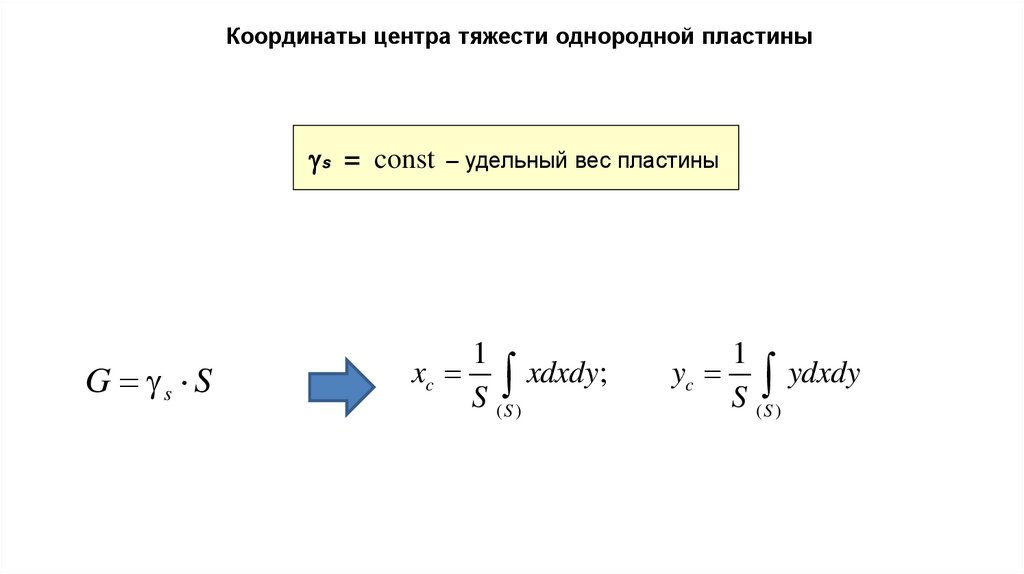
Координаты центра тяжести однородной пластины
s = const – удельный вес пластины
G s S
1
xc xdxdy;
S (S )
1
yc ydxdy
S (S )

11.

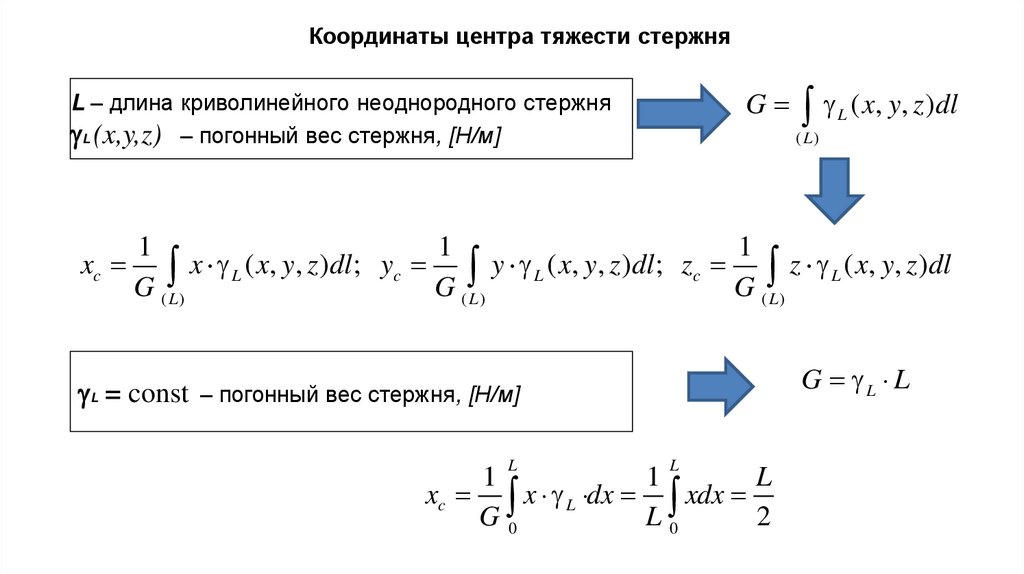
Координаты центра тяжести стержня
G L ( x, y, z )dl
L – длина криволинейного неоднородного стержня
L (x,y,z) – погонный вес стержня, [Н/м]
xc
( L)
1
1
1
x
(
x
,
y
,
z
)
dl
;
y
y
(
x
,
y
,
z
)
dl
;
z
z L ( x, y, z )dl
L
c
L
c
G ( L)
G ( L)
G ( L)
G L L
L = const – погонный вес стержня, [Н/м]
L
L
1
1
L
xc x L dx xdx
G0
L0
2

12.

7.3. Методы нахождения центра тяжести -1
1.
Метод симметрии для однородных тел
Плоская симметрии – центр тяжести имеет две координаты и лежит в плоскости симметрии
Несколько плоскостей симметрии (лучевая симметрия)– центр тяжести лежит на линии
пересечения плоскостей симметрии
Осевая симметрия – центр тяжести имеет одну координату и лежит на оси
Многоосевая симметрия – центр тяжести лежит в точке пересечения осей симметрии

13.

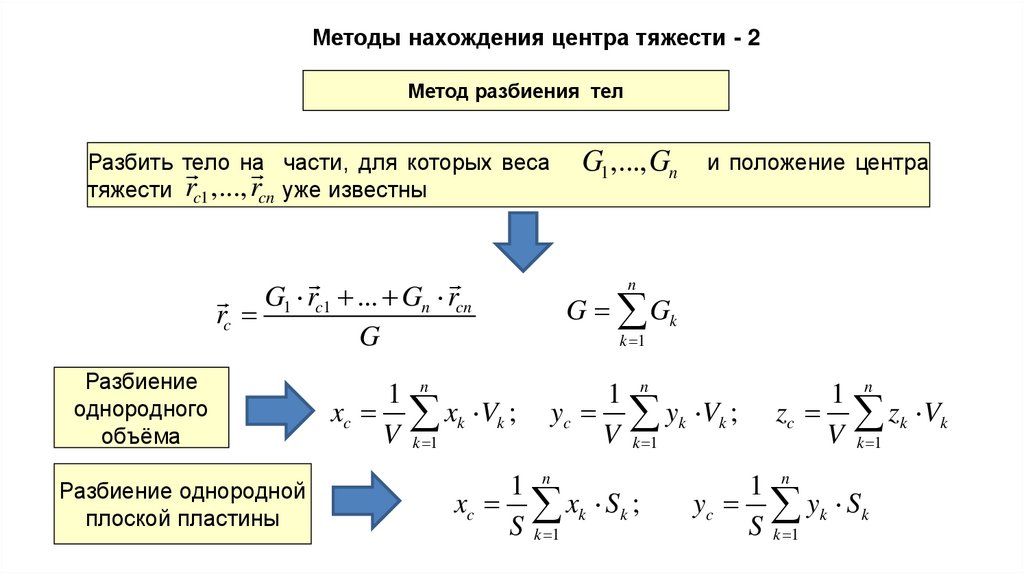
Методы нахождения центра тяжести - 2
Метод разбиения тел
Разбить тело на части, для которых веса
тяжести rc1 ,..., rcn уже известны
G r ... Gn rcn
rc 1 c1
G
Разбиение
однородного
объёма
Разбиение однородной
плоской пластины
1 n
xc xk Vk ;
V k 1
G1 ,..., Gn
и положение центра
n
G Gk
k 1
1 n
yc yk Vk ;
V k 1
1 n
xc xk Sk ;
S k 1
1 n
zc zk Vk
V k 1
1 n
yc yk Sk
S k 1

14.

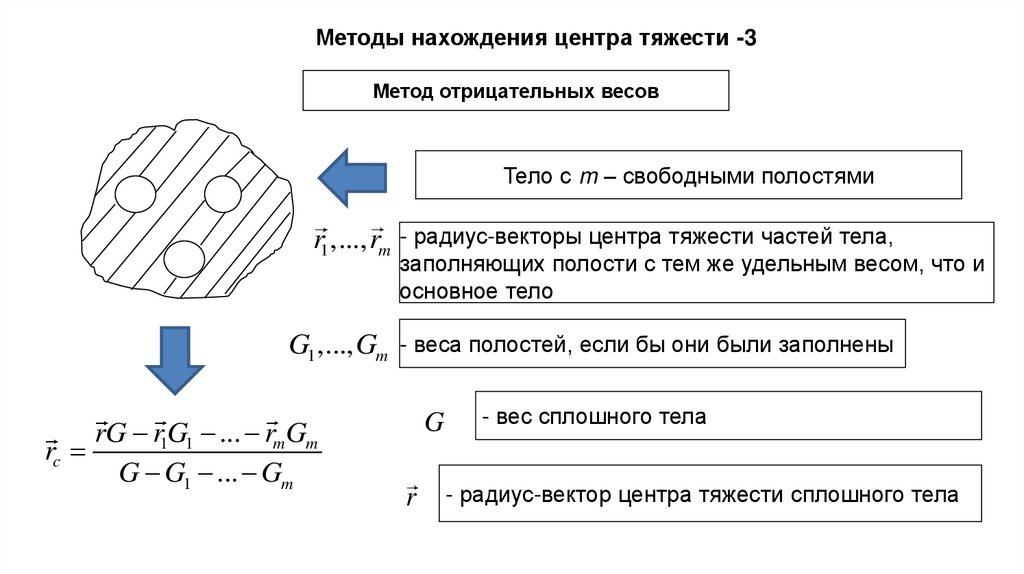
Методы нахождения центра тяжести -3
Метод отрицательных весов
Тело с m – свободными полостями
r1 ,..., rm - радиус-векторы центра тяжести частей тела,
заполняющих полости с тем же удельным весом, что и
основное тело
G1 ,..., Gm - веса полостей, если бы они были заполнены
rG rG
1 1 ... rmGm
rc
G G1 ... Gm
G
r
- вес сплошного тела
- радиус-вектор центра тяжести сплошного тела

15.

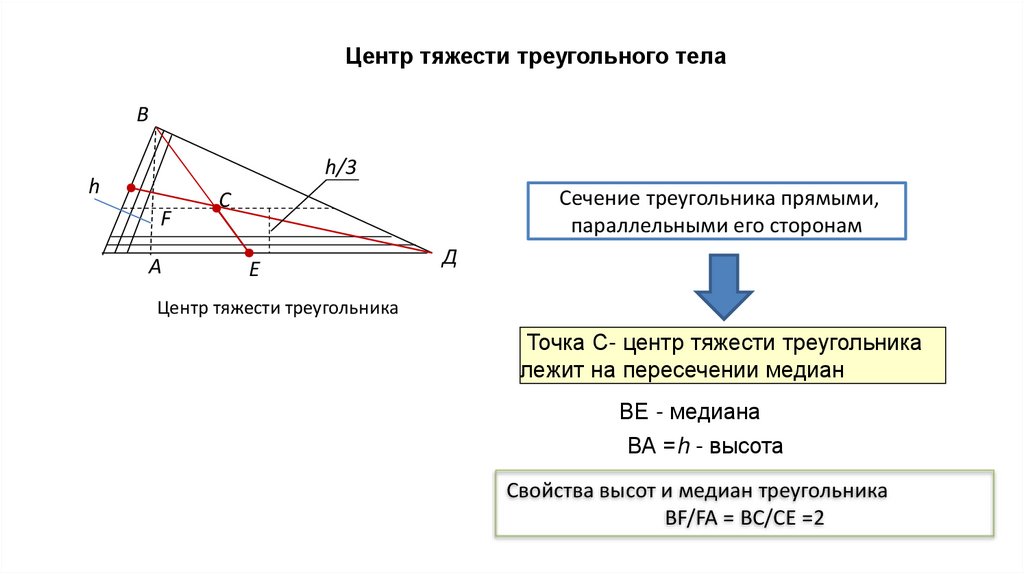
Центр тяжести треугольного тела
В
h/3
h
F
A
Сечение треугольника прямыми,
параллельными его сторонам
C
E
Д
Центр тяжести треугольника
Точка С- центр тяжести треугольника
лежит на пересечении медиан
ВЕ - медиана
ВА =h - высота
Свойства высот и медиан треугольника
ВF/FA = BC/CE =2

16.

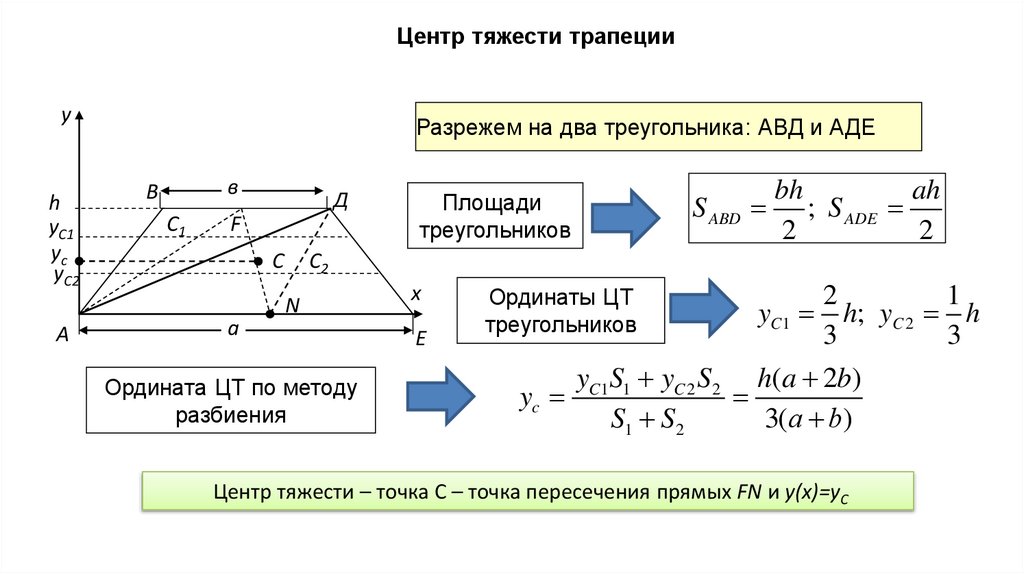
Центр тяжести трапеции
y
h
yС1
yc
yС2
А
Разрежем на два треугольника: АВД и АДЕ
в
В
C1
Д
F
C
а
S ABD
Площади
треугольников
bh
ah
; S ADE
2
2
C2
N
Ордината ЦТ по методу
разбиения
x
Е
Ординаты ЦТ
треугольников
yc
2
1
yC1 h; yC 2 h
3
3
yC1S1 yC 2 S2 h(a 2b)
S1 S2
3(а b)
Центр тяжести – точка С – точка пересечения прямых FN и y(x)=yС

17.

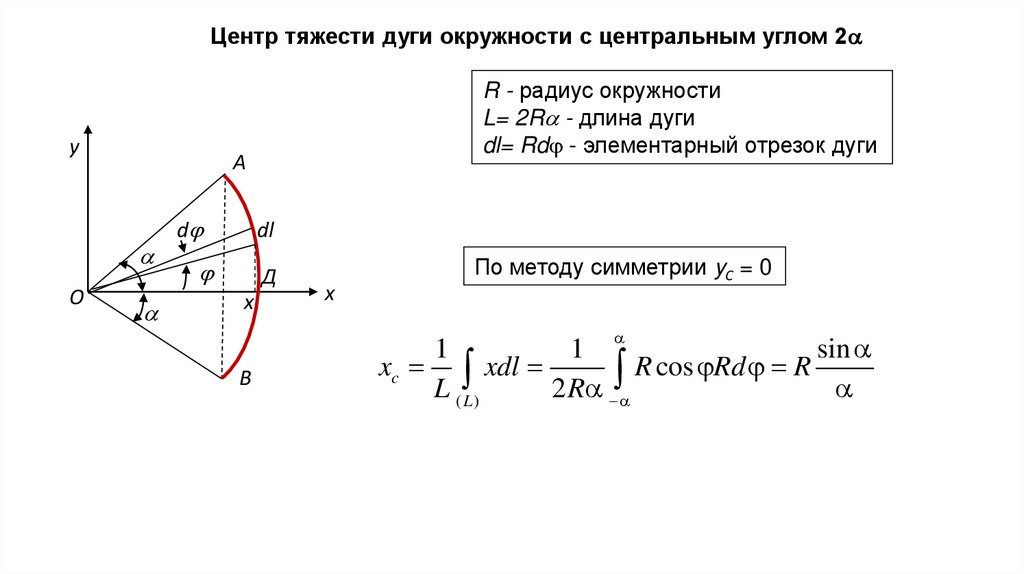
Центр тяжести дуги окружности с центральным углом 2
y
А
O
R - радиус окружности
L= 2R - длина дуги
dl= Rd - элементарный отрезок дуги
d
dl
Д
x
x
По методу симметрии yС = 0
В
1
1
sin
xc xdl
R cos Rd R
L ( L)
2 R

18.

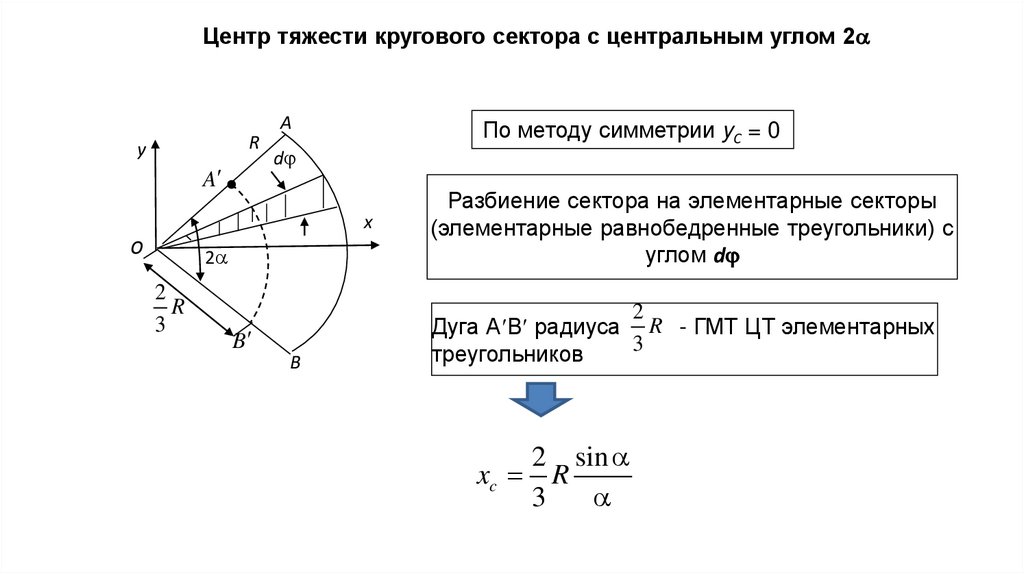
Центр тяжести кругового сектора с центральным углом 2
R
y
A
А
По методу симметрии yС = 0
d
x
o
2
2
R
3
B
B
Разбиение сектора на элементарные секторы
(элементарные равнобедренные треугольники) с
углом d
2
Дуга А В радиуса R - ГМТ ЦТ элементарных
3
треугольников
2 sin
xc R
3