Приведение произвольной системы сил к центру

1.

Новосибирский Государственный Архитектурно-Строительный
Университет (Сибстрин)
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
СТАТИКА
ЛЕКЦИЯ 6.
ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ
СИСТЕМЫ СИЛ К ЦЕНТРУ
Кафедра теоретической механики

2. План лекции

Введение. Две основные задачи статики.
Лемма о параллельном переносе силы.
Главный вектор и главный момент системы.
Основная теорема статики. Метод Пуансо.
Условия равновесия различных систем сил.
Статические инварианты.
Частные случаи приведения.
Контрольные вопросы к лекции.

3. На предыдущей лекции

В статике твердого тела, которую мы изучаем,
решаются две основные задачи. (см. Лекцию 1).
Сегодня мы выясним, как решается первая
задача статики –
приведение к простейшему виду любой
заданной системы сил.
ВВЕДЕНИЕ

4. Цель лекции

Доказать основную теорему статики.
Получить универсальный метод решения
задач на равновесие тел – метод Пуансо.
Выяснить, какими являются аналитические
условия равновесия различных систем сил.
ВВЕДЕНИЕ

5.

Зададим вопрос: к какому простейшему виду можно привести
любую заданную систему сил?
Для ответа на него вспомним, какие операции (действия) с
силами допустимы.
Не изменяя действие силы на тело, силу можно переносить
вдоль линии ее действия в любую точку.
Силы, линии действия которых пересекаются, можно
геометрически складывать (по правилу
параллелограмма).
На вопрос, как перенести силу параллельно самой себе в
другую точку приложения, отвечает Лемма о
параллельном переносе силы.
ВВЕДЕНИЕ

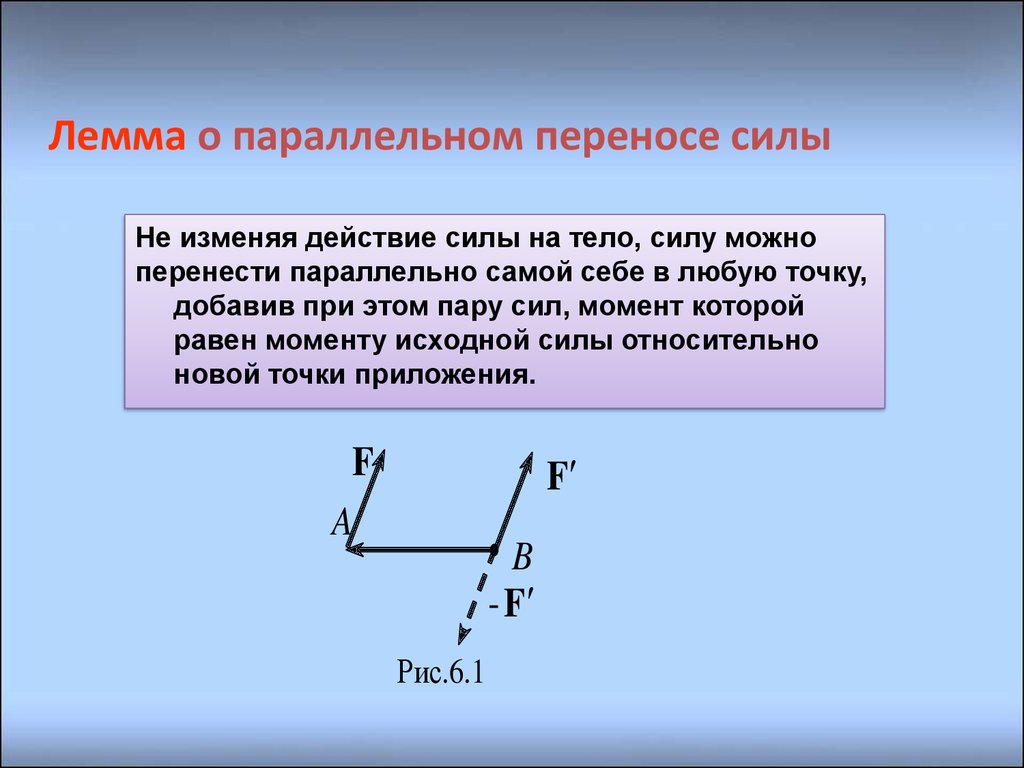
6. Лемма о параллельном переносе силы

Не изменяя действие силы на тело, силу можно
перенести параллельно самой себе в любую точку,
добавив при этом пару сил, момент которой
равен моменту исходной силы относительно
новой точки приложения.
F
F
A
B
- F
Рис.6.1

7. Сальвадор Дали

Невольничий рынок с явлением
незримого бюста Вольтера

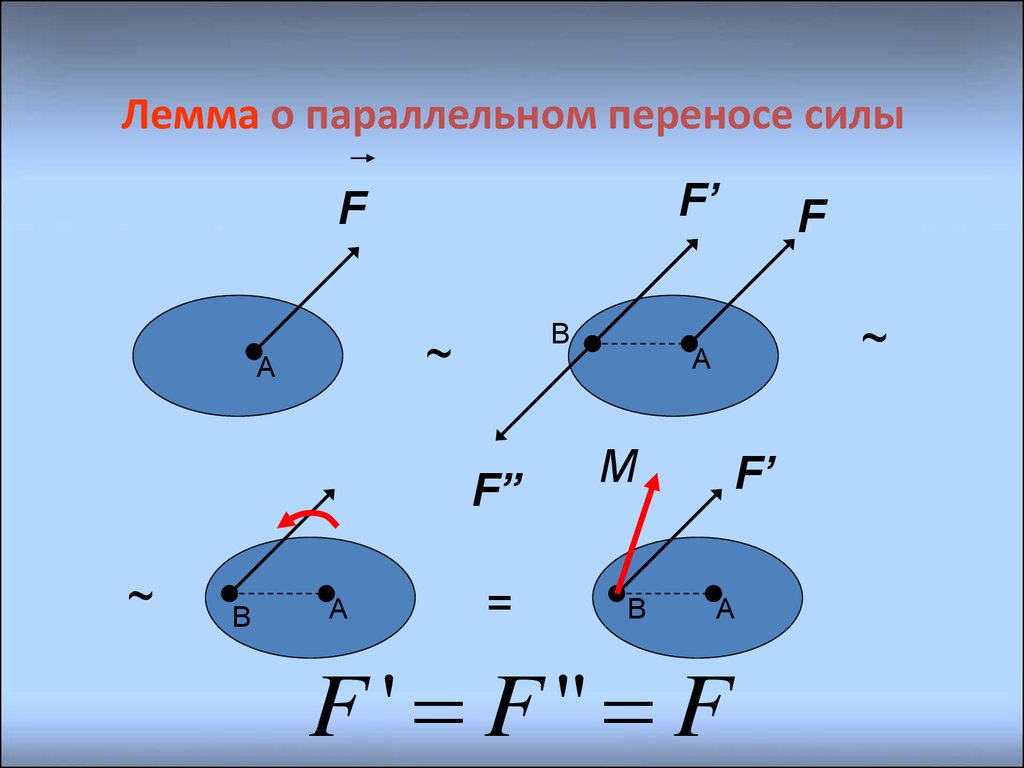
8. Лемма о параллельном переносе силы

F’
F
B
~
A
F”
~
B
A
=
F
~
A
F’
M
B
A
F ' F" F

9. Лемма о параллельном переносе силы

F F’
F
˜
o
B
F’’
F
˜
O
M
=
A
A
Доказательство. Пусть сила F приложена в точке А.
(Добавим к ней уравновешенную систему сил,
приложенную в точке B: {F’, -F’} ~ 0, F = F’. Тогда F~
{F,F’,−F’} = {(F,−F’),F’}, поскольку силы F,-F’
образуют пару сил с моментом m (F,-F’) =
BA F m B (F)
Лемма доказана.

10. Иллюстрация

Если удерживать рукой однородный брусок весом P за его
середину (рис. а), то нужно просто тянуть вверх с силой Q = P.
Чтобы удержать брусок в равновесии в случае (рис. б), необходимо
не только тянуть вверх с силой Q = P, но и создавать момент
m P AB / 2.
а)
A
б)
m
Q
Q
B
B
A
P
P
Рис. 6.2

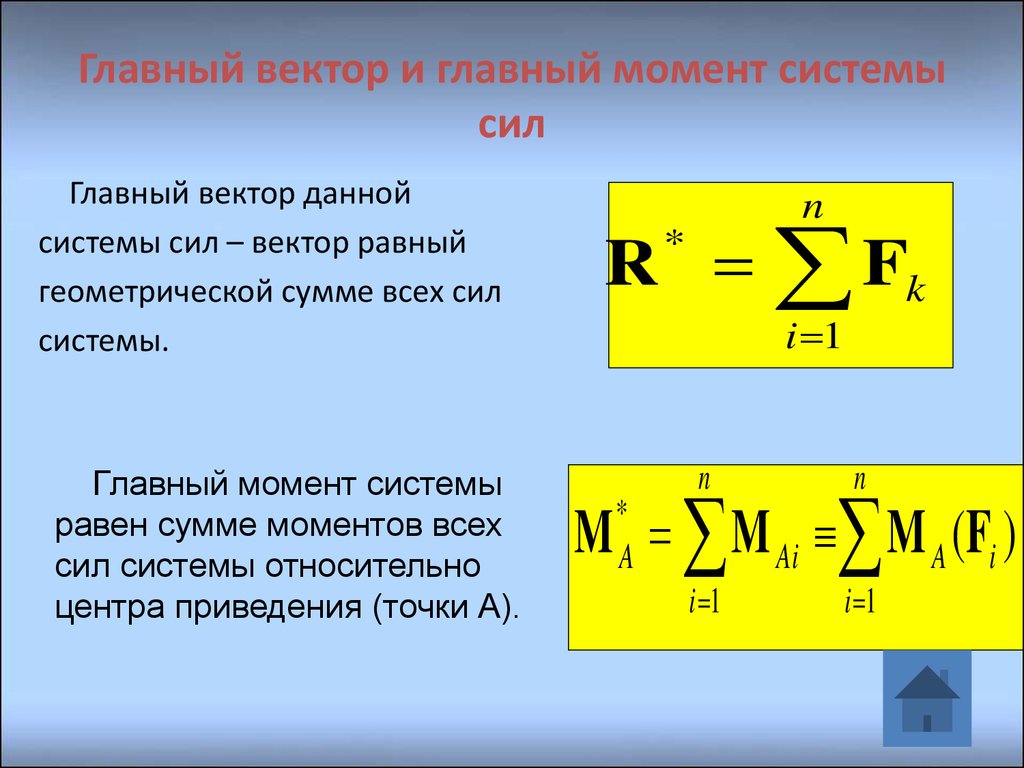
11. Главный вектор и главный момент системы сил

Главный вектор данной
системы сил – вектор равный
геометрической сумме всех сил
системы.
Главный момент системы
равен сумме моментов всех
сил системы относительно
центра приведения (точки А).
n
R Fk
*
i 1
n
n
i 1
i 1
M M Ai M A (Fi )
*
A

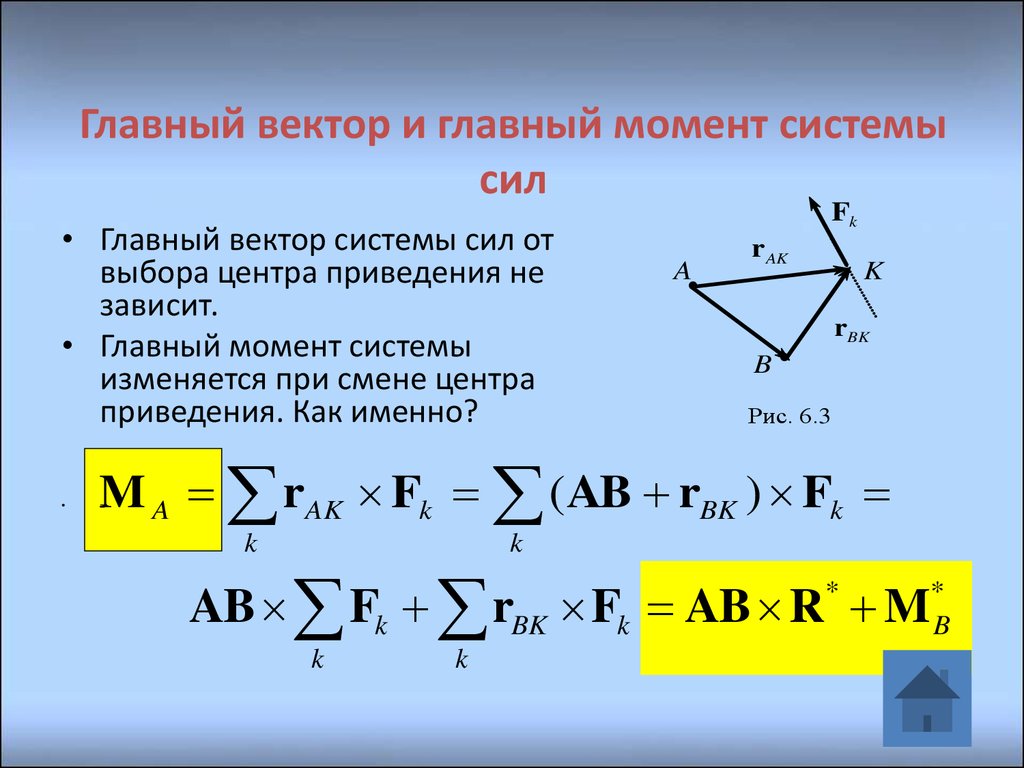
12. Главный вектор и главный момент системы сил

• Главный вектор системы сил от
выбора центра приведения не
зависит.
• Главный момент системы
изменяется при смене центра
приведения. Как именно?
Fk
A
r AK
K
rBK
B
Рис. 6.3
M A rAK Fk ( AB rBK ) Fk
=
k
k
AB Fk rBK Fk AB R M
*
k
k
*
B

13. Основная теорема статики

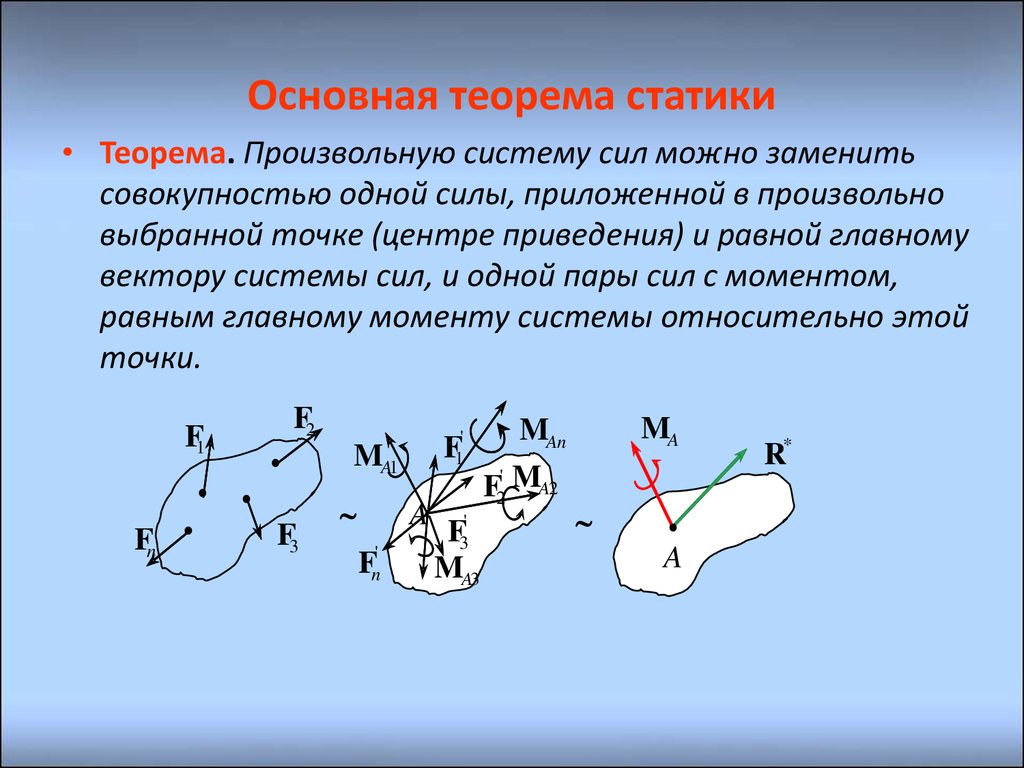
• Теорема. Произвольную систему сил можно заменить
совокупностью одной силы, приложенной в произвольно
выбранной точке (центре приведения) и равной главному
вектору системы сил, и одной пары сил с моментом,
равным главному моменту системы относительно этой
точки.
F1
Fn
F2
F1'
MA1
F3
~
A
Fn'
F3'
MA3
MA
MAn
F2' MA2
~
A
R*

14. Доказательство

Дана система сил {F , F ,…, F }.Выберем произвольную
точку А за центр приведения. Согласно теореме о
параллельном переносе силы, перенесем все силы
параллельно в точку А. В результате получим систему
сходящихся сил (,,…,) и систему пар сил () (рис. 6.4).
Систему сходящихся сил заменим силой R:
n
n
R F Fk R *
i 1
'
k
i 1
а систему пар – результирующей парой, момент
которой равен М:
n
n
i 1
i 1
M M A (Fk ) M Ak M *A

15. Критерий эквивалентности

Основная теорема статики позволяет сформулировать
Критерий эквивалентности действия на абсолютно
твердое тело различных систем сил:
для эквивалентности двух систем сил, приложенных к
твердому телу, необходимо и достаточно, чтобы их
главные векторы и главные моменты относительно
некоторой точки были одинаковы.
Основная теорема статики является конструктивной,
она дает простой способ аналитического определения
главного вектора и главного момента любой системы сил.

16. Аналитическое определение главного вектора и главного момента

R * Fk iRx* jR *y kRz* iFkx jFky kFkz
k
k
*
*
*
M*A iM Ax
jM Ay
k
M
Az M A (Fk )
=
=
iM
iM
k
=
x
k
Ax
(Fk ) jM Ay (Fk ) kM Az (Fk )
(Fk ) jM y (Fk ) kM z (Fk )
k
Т.о. вычисление главного вектора и главного момента
системы сил сводится к умению находить проекции
сил на оси координат и моменты сил относительно
координатных осей.

17. Немного истории

Французский механик
Луи Пуансо (Poinsot)
(1777-1859) доказал
основную теорему
статики в 1804 г.

18. ПРИМЕР

Задача. Привести к центру О систему сил P, F1, F2, F3
(рис. 6.5), если Р = 30 Н, F1 = F2 = = F3 = 20 Н, а = 0,3 м,
b = 0,5 м, = 60°.
Решение. Найдем главный
вектор и главный момент
P
системы сил, действующих на пластину. Т.к. данная
система сил плоская, то
- 40
R x* F1 cos F2 cos
F3(н),
R *y F1 sin F2 sin P 30
(н),
(н.м).
M O* aF1 cos 2bF2 sin aF3 bP
11,3
O
F2
P
Рис. 6.5
Т.о. исходная система сил
F3
заменяется силой
x
и парой
сил с моментом
M O*
11,3
н.м
a
y
F1
R * { 40, 30}

19. Условия равновесия произвольной системы сил

Любая система сил будет эквивалентна нулю, если
равны нулю ее главный вектор и главный момент.
R*
n
n
Fk 0
M *O M Oi 0
i 1
i 1
В координатной форме эти условия равновесия
имеют вид:
n
F
k 1
n
M
k 1
x
kx
0,
(Fk ) 0,
n
F
k 1
0,
ky
k 1
F
k 1
n
M
n
kz
0,
n
y
(Fk ) 0, M z (Fk ) 0
k 1

20. Условия равновесия различных систем сил

• Для системы параллельных сил в пространстве (линии
действия параллельны оси Oz):
n
F
k 1
kz
0,
n
M
k 1
x
(Fk ) 0,
n
M
k 1
y
(Fk ) 0
• Для пространственной системы сходящихся сил:
n
n
n
k 1
k 1
k 1
Fkx 0, Fky 0, Fkz 0.
Остальные три условия равновесия выполняются
тождественно.

21. Условия равновесия произвольной плоской системы сил

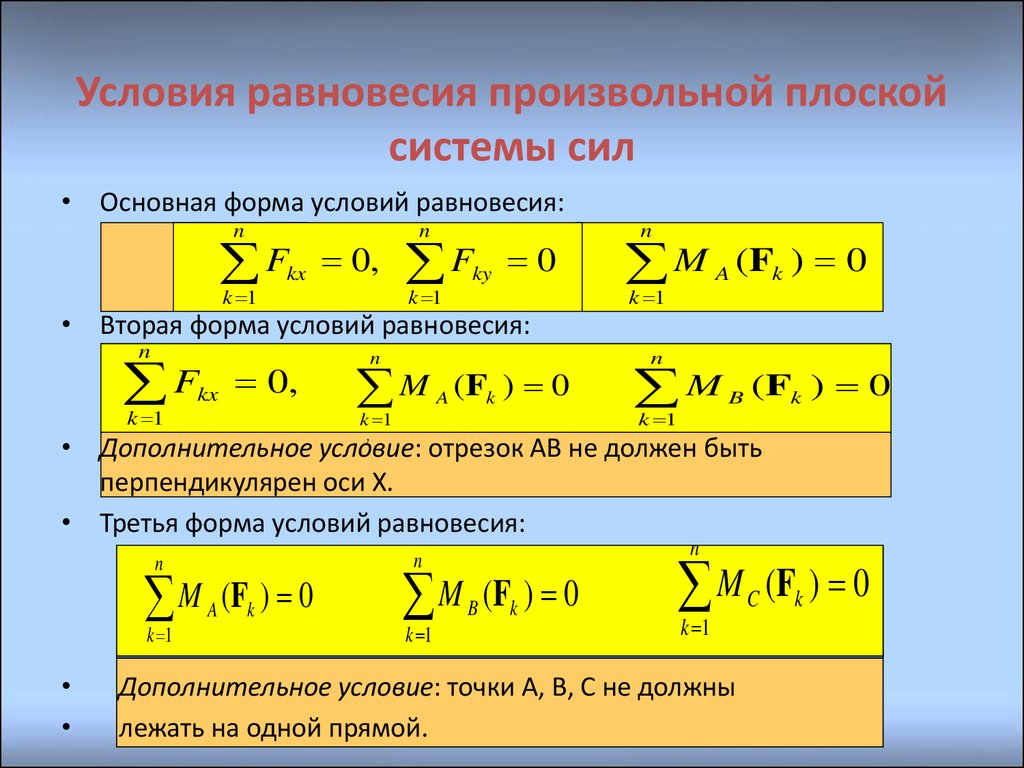
• Основная форма условий равновесия:
n
F
k 1
kx
0,
n
F
ky
k 1
0
n
M
k 1
A
(Fk ) 0
• Вторая форма условий равновесия:
n
F
k 1
kx
0,
n
M
k 1
A
(Fk ) 0
,
n
M
k 1
B
(Fk ) 0
• Дополнительное условие: отрезок АВ не должен быть
перпендикулярен оси Х.
• Третья форма условий равновесия:
n
M A (Fk ) 0
k 1
n
M
k 1
n
B (Fk ) 0
M
k 1
Дополнительное условие: точки А, В, С не должны
лежать на одной прямой.
C
(Fk ) 0

22. Статические инварианты

Инварианты – величины, неизменные при некотором
преобразовании. Статические инварианты – величины,
не зависящие от выбора центра приведения.
I статический инвариант – главный вектор системы сил.
R * Fk
II статический инвариант - скалярное произведение главного
вектора и главного момента системы.
M *A R * M *B R *
M R cos(M R ) M R cos(M R )
*
A
*
*
A
*
*
B
*
*
B
*

23.

Статические инварианты
Убедимся в том, что R* .
-M *Aстатический инвариант.
M *A M *B AB R *
Умножая скалярно обе части этого соотношения на
главный вектор R*, получим:
M *A R * M *B R * (AB R * ) R *
( AB R* ) R* 0
следовательно,
т.к.
M R M R
*
A
*
*
B
AB R * R *
*
т. е. скалярное произведение M* и R* от выбора центра
приведения не зависит.

24. Частные случаи приведения

1.
*
M
R 0, O –0 уравновешенная система сил.
*
*
M
2. R 0, O –0Система сил приводится к
*
равнодействующей, проходящей через точку О.
3.
R 0, M *O – 0система сил приводится к паре с
*
моментом M,*Oглавные моменты сил относительно любых
M *A M *O AO R * M *O
точек равны. Действительно,
4. R * 0, M O 0 R MВOэтом случае равен
нулю II статический инвариант и данная система сил
также приводится к равнодействующей.
*
*
*

25. Частные случаи приведения

*
*
R
0
,
M
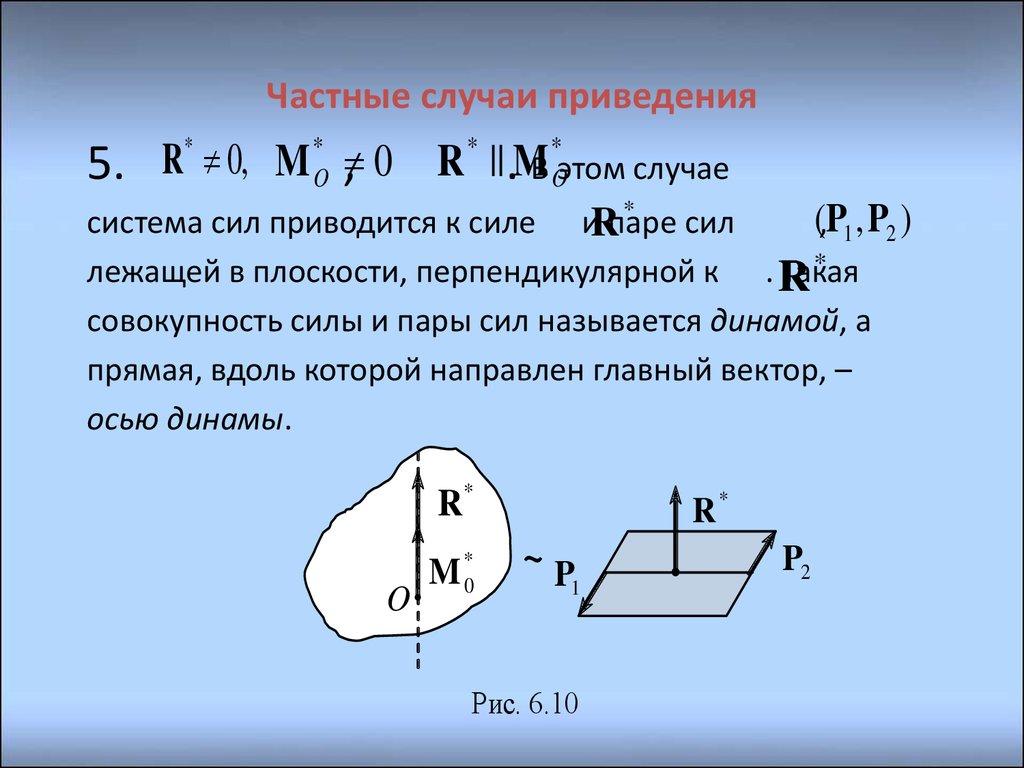
5.
O , 0
R * || .MВ *Oэтом случае
*
(,P1 , P2 )
система сил приводится к силе иRпаре
сил
*
лежащей в плоскости, перпендикулярной к . R
Такая
совокупность силы и пары сил называется динамой, а
прямая, вдоль которой направлен главный вектор, –
осью динамы.
R*
O
M *0
R*
~P
1
Рис. 6.10
P2

26. ПОДВЕДЕМ ИТОГИ

Мы выяснили, как решается первая задача статики –
к какому простейшему виду приводится любая система сил:
в общем случае – к совокупности одной силы и одной пары сил.
Если произвольная система сил не уравновешена, то она
приводится либо к паре сил, либо к равнодействующей, либо к
динаме.
Теперь мы знаем, как выглядят аналитические условия
равновесия для любой возможной системы сил.
Эти знания понадобятся нам при решении практических задач
о равновесии тела или системы тел, находящихся под действием
любых заданных сил и нагрузок. Эти вопросы будут рассмотрены
на следующей лекции, тема которой –
РАВНОВЕСИЕ СИСТЕМ ТЕЛ

27. Тема следующей лекции

РАВНОВЕСИЕ СИСТЕМ ТЕЛ
ЗАКЛЮЧЕНИЕ

28. Вопросы для самоконтроля

1. Сформулируйте лемму о параллельном
переносе силы.
2. Что такое главный вектор системы сил?
3. Что такое главный момент системы сил?
4. Сформулируйте основную теорему статики.
5. Когда главный вектор системы сил является и
равнодействующей?
6. Когда система сил приводится к паре?
7. Сколько линейно независимых уравнений
равновесия можно составить для плоской
(пространственной) системы параллельных сил?
8. Что такое статические инварианты?
9. Что такое первый статический инвариант?
10. Что такое второй статический инварианты?

29.

Спасибо за внимание!