Кинематика и динамика точки

1. Новосибирский Государственный Архитектурно- Строительный Университет (Сибстрин)

Новосибирский Государственный АрхитектурноСтроительный Университет (Сибстрин)
Лекция 6.
КИНЕМАТИКА И ДИНАМИКА
ТОЧКИ
Я никогда не должен говорить, что тело
находится в состоянии покоя или движения,
не прибавляя, к каким именно телам оно
покоится или изменяет свое положение.
Эммануил Кант
Кафедра теоретической механики

2.

Иммануи́л Кант
1724-1804, Кёнигсберг
2

3.

3

4. 1.1.2. Курс ТМ включает

• Кинематика
Кинематика исследует движение тел лишь с
геометрической точки зрения, без учета сил
вызывающих это движение
• Динамика
Динамика отвечает на основной вопрос курса –
из-за чего возникает и как изменяется движение
• Статика
Статика изучает условия равновесия (покоя) тел.
Фактически это частный случай движения, т.к.
покой и равномерное и прямолинейное движение
эквивалентны
4

5. 6.1. Введение в кинематику точки

6. 6.1.1. Задачи кинематики

Кинематика – это раздел теоретической механики, в
котором изучается движение тела с геометрической
точки зрения, т.е. без учета сил, действующих на тело
Движение материальной точки – это изменение ее положения
относительно какого-либо другого тела (тела отсчета) с
течением времени
Положение объекта задается расстоянием до некоторого
другого объекта и является относительным. Относительным
является и само движение
Задачи кинематики
1. Определение математических способов задания
движения тела
2. Определение для заданного способа задания движения
тела его кинематических характеристик
2.1.
ССС
6.1. ОПРЕДЕЛЕНИЕ
ВВЕДЕНИЕ В КИНЕМАТИКУ
ТОЧКИ
5

7. 6.1.2. Относительность движения

• Совокупность тела отсчета и жестко связанных с ним
координатных осей и часов называется системой отсчета
• Движение одного и того же тела относительно разных объектов
(тел) может быть совершенно различным
В системе отсчета поезда
В системе отсчета обходчика
2.1.
ССС
6.1. ОПРЕДЕЛЕНИЕ
ВВЕДЕНИЕ В КИНЕМАТИКУ
ТОЧКИ
6

8. 6.1.3. Пространство и время

• Постулируется существование не связанных между собой
абсолютного пространства и абсолютного времени
Свойства пространства и времени не зависят и от того, как
движутся тела
Пространство является трехмерным евклидовым пространством,
оно однородное и изотропное
Время также однородное и одинаково во всех точках пространства
Время изменяется непрерывно, а наблюдатель измеряет
"расстояние" между различными моментами времени часами
Часы универсальны и их показания не зависят от того,
расположены они в покоящихся или движущихся объектах
Однородность времени означает отсутствие выделенных моментов
времени. Выбор начала отсчета времени поэтому диктуется лишь
конкретной решаемой задачей
2.1.
ССС
6.1. ОПРЕДЕЛЕНИЕ
ВВЕДЕНИЕ В КИНЕМАТИКУ
ТОЧКИ
7

9. 6.2. Способы задания движения точки

10. 6.2.1. Векторный и координатный способы

z
k
i
• Пусть точка М движется относительно
системы отсчета Oxyz
М
• С течением времени положение точки М
относительно данной системы отсчета
меняется
O
j
y
x
Геометрическое место последовательно
занимаемых движущейся материальной
точко й п ол ожен и й в п р о ст р а н с т в е
относительно некоторого тела отсчета
След за атомной подводной лодкой
называется ее траекторией
ВЕКТОРНЫЙ
СПОСОБ
ЗАДАНИЯ ДВИЖЕНИЯ
2.1.
ССС
6.2. ОПРЕДЕЛЕНИЕ
СПОСОБЫ ЗАДАНИЯ
ДВИЖЕНИЯ ТОЧКИ
8

11. 6.2.1. Векторный и координатный способы

z
k
i
• Пусть точка М движется относительно
системы отсчета Oxyz
М
• С течением времени положение точки М
относительно данной системы отсчета
меняется
r (t )
O
y
j
x
r r t
Падение
метеорита
x x (t ), y y (t ), z z (t )
ВЕКТОРНЫЙ
СПОСОБ
ЗАДАНИЯ ДВИЖЕНИЯ
2.1.
ССС
6.2. ОПРЕДЕЛЕНИЕ
СПОСОБЫ ЗАДАНИЯ
ДВИЖЕНИЯ ТОЧКИ
9

12. 6.3. Скорость точки

13. 6.3.1. Апории Зенона

Догонит ли Ахиллес черепаху?
• Как охарактеризовать движение различных тел, преодолевающих
равные отрезки за разное время?
• Скорость материальной точки – это векторная кинематическая
характеристика движения точки, определяющая быстроту
изменения ее положения относительно заданной системы
координат
7.3. СКОРОСТЬ ТОЧКИ
6.3. СКОРОСТЬ ТОЧКИ
10

14.

Зенон Элейский
V век до н.э.
11

15. 6.3.2. Векторный способ задания скорости

z
M(t)
v
r
О
x
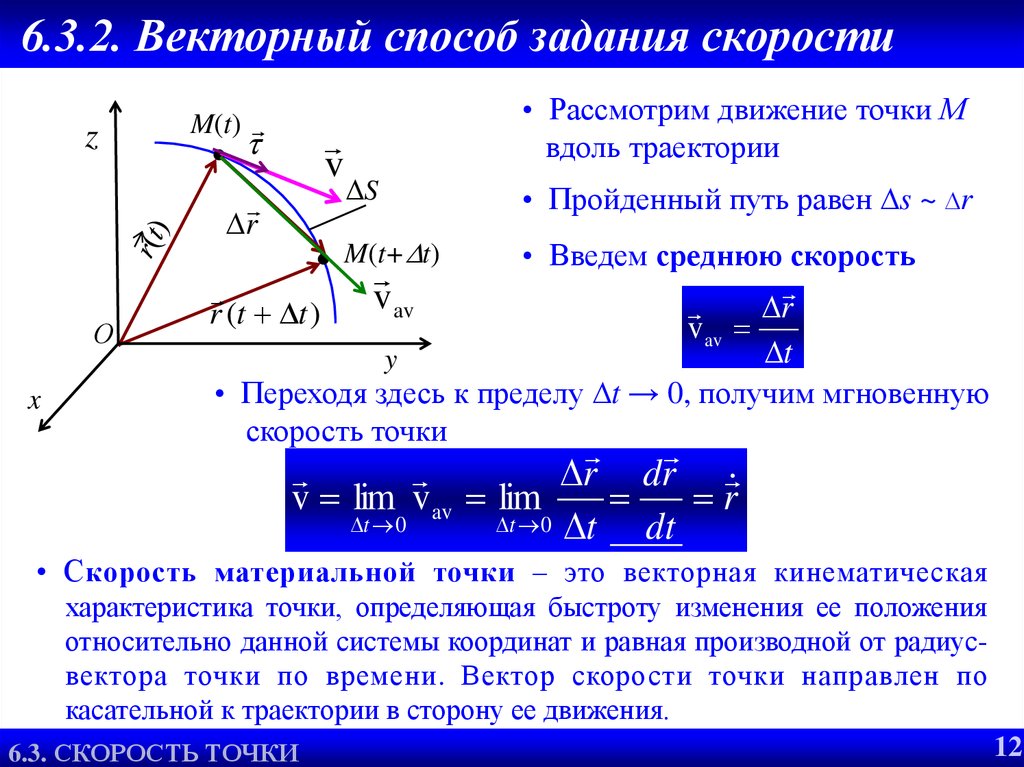
• Рассмотрим движение точки М
вдоль траектории
ΔS
• Пройденный путь равен s ~ r
M(t+ t)
• Введем среднюю скорость
v
av
r
r (t t )
v av
t
y
• Переходя здесь к пределу t → 0, получим мгновенную
скорость точки
r dr
v lim v av lim
r
t 0
t 0 t
dt
• С корость материальной точки – это векторная кинематическая
характеристика точки, определяющая быстроту изменения ее положения
относительно данной системы координат и равная производной от радиусвектора точки по времени. Вектор скорости точки направлен по
касательной к траектории в сторону ее движения.
2.1.
ССС
6.3. ОПРЕДЕЛЕНИЕ
СКОРОСТЬ ТОЧКИ
12

16. 6.3.3. Координатный способ задания скорости

dr
v
r i v x jv y kvz
dt
• Чтобы найти проекции скорости, продифференцируем радиусвектор точки
d
v r ( xi yj zk ) x i y j z k v x i v y j v z k
dt
v x x , v y y , v z z
v v 2x v 2y v 2z x 2 y 2 z 2
vx
vy
vz
cos( v, i ) , cos( v, j ) , cos( v, k )
v
v
v
2.1.
ССС
6.3. ОПРЕДЕЛЕНИЕ
СКОРОСТЬ ТОЧКИ
13

17. 6.4.1. Векторный способ задания ускорения

M(t)
v(t t )
v
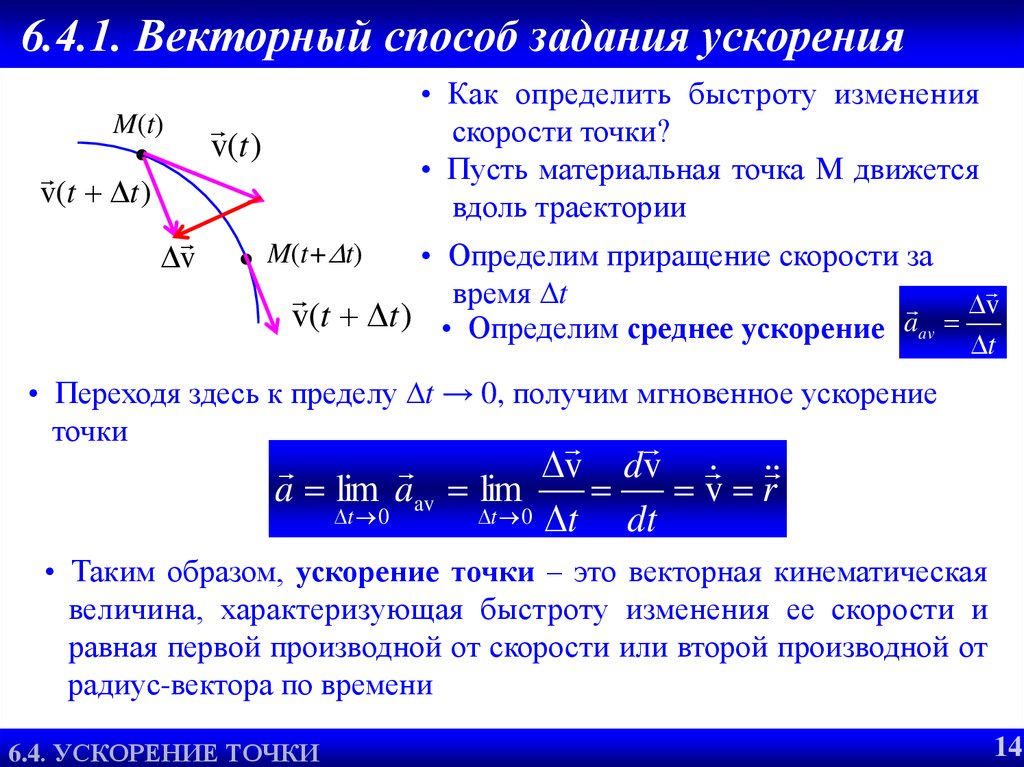
• Как определить быстроту изменения
скорости точки?
• Пусть материальная точка М движется
вдоль траектории
v(t )
M(t+ t)
• Определим приращение скорости за
время t
v
v(t t ) • Определим среднее ускорение aav
t
• Переходя здесь к пределу t → 0, получим мгновенное ускорение
точки
v dv
a lim aav lim
v r
t 0
t 0 t
dt
• Таким образом, ускорение точки – это векторная кинематическая
величина, характеризующая быстроту изменения ее скорости и
равная первой производной от скорости или второй производной от
радиус-вектора по времени
2.1.
ССС
6.4. ОПРЕДЕЛЕНИЕ
УСКОРЕНИЕ ТОЧКИ
14

18. 6.4.2. Координатный способ задания ускорения

• Чтобы получить выражение ускорения при координатном способе
задания движения точки, выразим вектор ускорения через его
проекции на оси координат
a i ax j a y k az
• С другой стороны,
a v i v x j v y k v z
• Сравнивая эти два выражения, находим
a x v x , a y v y , a z v z ,
a a x2 a y2 a z2 v 2x v 2y v 2z x 2 y 2 z 2
ay
ax
az
cos( a , i ) , cos( a , j ) , cos( a , k )
a
a
a
2.1.
ССС
6.4. ОПРЕДЕЛЕНИЕ
УСКОРЕНИЕ ТОЧКИ
15

19. 6.5. Аксиомы динамики

20. 6.5.1. Закон инерции Галилея

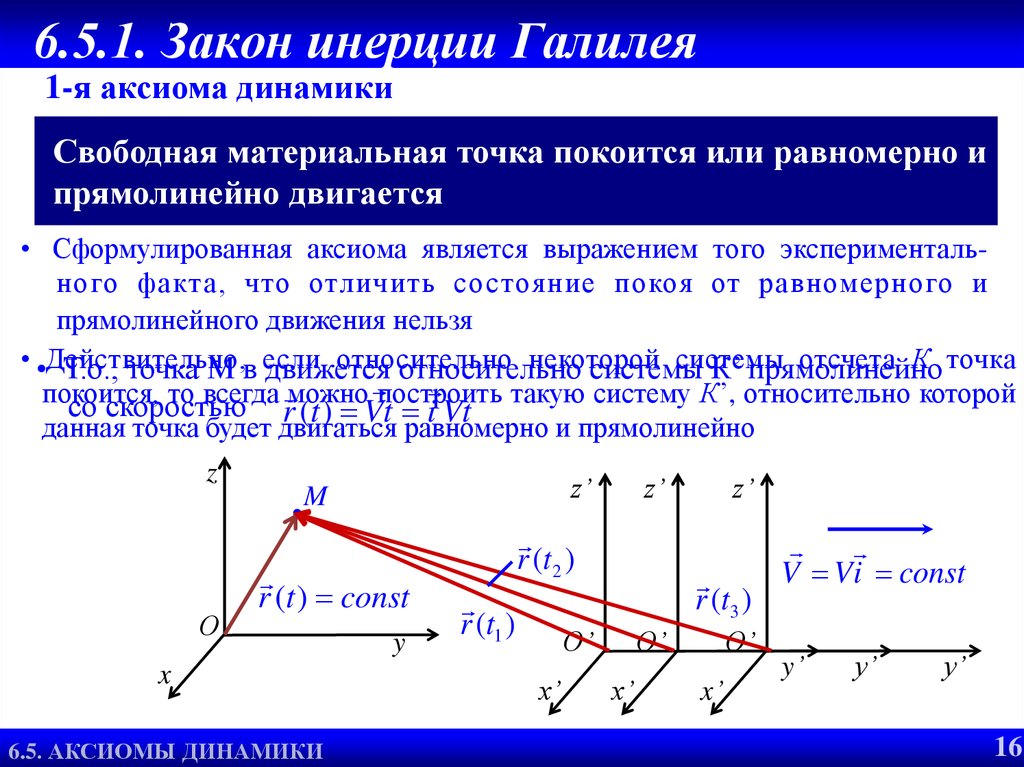
1-я аксиома динамики
Свободная материальная точка покоится или равномерно и
прямолинейно двигается
• Сформулированная аксиома является выражением того экспериментального факта, что отличить со стояние покоя от равномерного и
прямолинейного движения нельзя
• •Действительно,
относительно
некоторой
системы
отсчета К точка
Т.о., точка М в если
движется
относительно
системы
К’
прямолинейно
построить
покоится,
то
всегда
можно
со скоростью r (t ) Vt i Vt такую систему К’, относительно которой
данная точка будет двигаться равномерно и прямолинейно
z
О
z’
M
r (t ) const
x
2.1.
ОПРЕДЕЛЕНИЕ
ССС
6.5. АКСИОМЫ
ДИНАМИКИ
y
z’
r (t 2 )
r (t1 )
r (t3 )
О’
x’
z’
О’
x’
О’
x’
V Vi const
y’
y’
y’
16

21. 6.5.2. Принцип относительности Галилея

• Системы отсчета, относительно которых свободная
материальная точка покоится или равномерно и
прямолинейно движется называются инерциальными
• Инерциальных систем отсчета существует бесконечно много и
все они движутся друг относительно друга с постоянной
скоростью
• Все инерциальные системы отсчета эквивалентны
Принцип относительности Галилея
Все законы механики одинаково формулироваться и
во всех инерциальных системах отсчета
2.1.
ССС
6.5. ОПРЕДЕЛЕНИЕ
АКСИОМЫ ДИНАМИКИ
17

22. 6.5.4 Второй закон Ньютона

Аксиома 2
Если в некоторой инерциальной системе отсчета на свободную
материальную точку действует сила F , то скорость изменения
импульса (количества движения) материальной точки равна
действующей на нее силе
dp
F
dt
или
dmv
F
dt
• Т.о., масса является мерой инерции тела. Инертность тела, т.е. его
способность двигаться без изменения скорости тем больше, чем
больше масса. По этой причине эту массу называют инертной
N
• Масса величина аддитивная и скалярная M mi
i 1
• В классической механике
предполагается,
что масса тела во всех
отсчета одинакова и не меняется со временем
dv
инерциальных
системах
m
mr F или ma F
dt
2.1.
ССС
6.5. ОПРЕДЕЛЕНИЕ
АКСИОМЫ ДИНАМИКИ
18

23. 6.5.6. Третий закон Ньютона

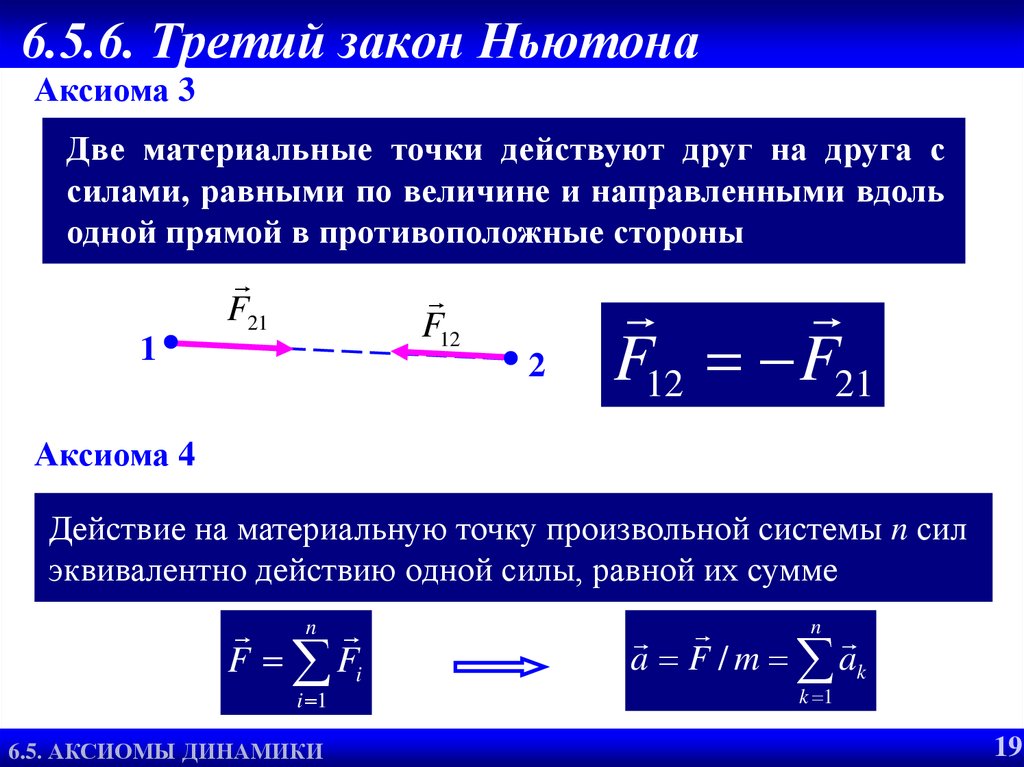
Аксиома 3
Две материальные точки действуют друг на друга с
силами, равными по величине и направленными вдоль
одной прямой в противоположные стороны
F21
F12
1
2
F12 F21
Аксиома 4
Действие на материальную точку произвольной системы n сил
эквивалентно действию одной силы, равной их сумме
n
F Fi
i 1
2.1.
ОПРЕДЕЛЕНИЕ
ССС
6.5. АКСИОМЫ
ДИНАМИКИ
n
a F / m ak
k 1
19

24.

Исаак Ньютон,
1642-1727, ВулсторнКембридж-Лондон
20

25. 6 .5.5. Силы, зависящие от скорости точки

F
M
Пусть точка массы m движется прямолинейно
v
x
x
под действием силы F = F(v)
• Уравнение Ньютона в данном случае имеет вид
dv
dx
m
F ( v), v
НУ: v( 0) v 0 , x (0) x0 ,
dt
dt
• Интегрируя первое уравнение:
0
v
dv
t
F ( v)
v0
m
• Закон движения имеет вид
f ( v) t
v v (t )
t
x x0 v(t )dt
0
Силы сопротивления в
сплошной среде
2.1.
ССС
6.5. ОПРЕДЕЛЕНИЕ
АКСИОМЫ ДИНАМИКА
Твердое
тело в газе
F v 2 v/ | v |
Твердое тело
в жидкости
F v
21

26. 6.5.6. Движение в вязкой жидкости

Задача 6.1
Материальная точка массы m, двигающаяся прямолинейно с постоянной
скоростью v, попадает
в вязкую жидкость, где на нее действует сила
сопротивления F m v . Найти закон движения точки в жидкости.
Решение
0
M
• Выберем за начало отсчета положение входа точки в жидкость
F
v
x
• Уравнение Ньютона в данном случае имеет вид
m v m v
v
НУ:
v( 0) v 0 , x (0) 0
t
dv
v v 0 dt
0
ln
v
t
v0
v v 0 e t
• Скорость движения точки в жидкости, т.о., экспоненциально затухает
• Закон движения находится интегрированием уравнения x v 0 e t
x V0
m
1 exp t
При t координата
2.1.
ССС
6.5. ОПРЕДЕЛЕНИЕ
ДИНАМИКА ПРЯМОЛИНЕЙНОГО
ДВИЖЕНИЯ
x V0
m
22

27. На предыдущих лекциях

• Изучены законы, описывающие движение
материальной точки относительно инерциальной
системы отсчета, в частности, относительно
покоящейся системы
“Согласно опытно установленному факту
не существует никакого физически
обнаруживаемого состояния движения,
которое можно было бы назвать
абсолютным покоем”.
Как же описывать движение относительно
неинерциальной системы отсчета?
23

28. 6.6.1. Измерение расстояния относительно НСО

z
z1
y1
M
z
y1
O1
ra
x1
O
O
x
j1
x1
i1
k1
z1
O1
rO1
k
y
rr
j
y
i
ra rO1 rr
x
неподвижную
системунеподвижной
отсчета
•• Введем
Движение
относительно
системы отсчета
называется
абсолютным
• Введем
неинерциальную
систему отсчета
• Движение относительно подвижной системы отсчета
• Наша задача описать движение точки относительно НСО
называется относительным
••Первое,
что необходимо
сделатьсистемы
– это задатьотсчета
движение относительно
точки
Движение
подвижной
неподвижной называется переносным движением
2.1.
ОПРЕДЕЛЕНИЕ
ССС
6.6.
КИНЕМАТИКА
ДВИЖЕНИЯ
ТОЧКИ ОТНОСИТЕЛЬНО НСО
СВОБОДНЫЕ
ЗАТУХАЮЩИЕ
КОЛЕБАНИЯ
24

29. 6.6.2. Скорость относительно НСО

M
dr
z
r
r
r
v
a
O1
r
r z
y1
ra
k
O
j
i
r
j1
x1
i1
a
1
k1
drO1
drr
a
dt
dt
dt
• Первый член равен
O1
drO1
rO1
x
y
v r x 1i1 y 1 j1 z 1k1
x i y j z k v O1
dt
• С другой стороны, rr x1i1 y1 j1 z1k1
drr
x 1i1 y 1 j1 z 1k1 x1i1 y1 j1 z1k1
dt
drr
v r x1i1 y1 j1 z1k1
dt
• Но изменение второго члена связано с изменением направлений
единичных векторов НСО относительно ИСО, т.е. с вращением
НСО относительно начала координат О1 с угловой скоростью
2.1.
ОПРЕДЕЛЕНИЕ
ССС
6.6.
КИНЕМАТИКА
ДВИЖЕНИЯ
ТОЧКИ ОТНОСИТЕЛЬНО НСО
СВОБОДНЫЕ
ЗАТУХАЮЩИЕ
КОЛЕБАНИЯ
25

30. 6.6.3. Переносная скорость

z
y1
ra
k
O
y
i1 i1 , j1 j1 , k1 k1
rr z1
drr
k1
v r x1 i1 y1 j1 z1 k1
dt
O1
i1
drr
v r x1i1 y1 j1 z1k1 v r rr
dt
M
j
i
j1
x1
rО1
v a v O1 rr v r
x
• Если точка М не движется относительно подвижной системы
отсчета, то v r 0 , и ее абсолютная скорость совпадает тогда со
скоростью движения подвижной системы отсчета относительно
неподвижной
• По определению это и есть скорость переносного движения
v e v O1 rr
Теорема. Абсолютная скорость точки равна
сумме относительной и переносной скоростей
2.1.
ОПРЕДЕЛЕНИЕ
ССС
6.6..
КИНЕМАТИКА
ДВИЖЕНИЯ
ТОЧКИ ОТНОСИТЕЛЬНО НСО
СВОБОДНЫЕ
ЗАТУХАЮЩИЕ
КОЛЕБАНИЯ
va ve vr
26

31. 6.6.4. Относительное ускорение

d
v
v a v O1 rr v r
a
a
• Первый член
dv O1
dt
d ( rr ) dv r
O1
dt
dt
dt
aO1 – это ускорение начала НСО относительно ИСО
d
(
r
)
d
d
r
r
• С другой стороны,
rr r r r v r r r
dt
dt
dt
• Наконец последний член
dv r d
x 1i1 y 1 j1 z 1k1 x 1i1 y 1 j1 z 1k1 x 1i1 y 1 j1 z 1k1
dt
dt
ar x 1i1 y 1 j1 z 1k ,
x 1i1 y 1 j1 z 1k1 x 1 i1 y 1 j1 z 1 k1
i1 x 1 j1 y 1 k1 z 1 v r
Время собирать камни
2.1.
ОПРЕДЕЛЕНИЕ
ССС
6.6.
КИНЕМАТИКА
ДВИЖЕНИЯ
ТОЧКИ ОТНОСИТЕЛЬНО НСО
СВОБОДНЫЕ
ЗАТУХАЮЩИЕ
КОЛЕБАНИЯ
27

32. 6.6.5. Теорема Кориолиса

dv O1
d ( rr ) dv r
dt
dt
dt
aa aO1 rr v r rr ar v r
aa
aa aO1 rr rr ar 2 v r
• Если точка покоится относительно подвижной системы отсчета, то ее
движение совпадает с переносным движением, а абсолютное ускорение –
с переносным ускорением
a a r r
e
O1
r
r
Теорема. Абсолютное ускорение точки равно сумме
относительного , переносного и кориолисова ускорений
a a a r ae ac
2.1.
ОПРЕДЕЛЕНИЕ
ССС
6.6.
КИНЕМАТИКА
ДВИЖЕНИЯ
ТОЧКИ ОТНОСИТЕЛЬНО НСО
СВОБОДНЫЕ
ЗАТУХАЮЩИЕ
КОЛЕБАНИЯ
28

33. 6.6.7. Ускорение Кориолиса

vr
ac 2 v r
ac
Это ускорение обращается в нуль, если
Гюстав Гаспар Кориолис
1792-1843
• угловая скорость подвижной системы отсчета
равна нулю ω=0, т. е. переносное движение поступательное
• угловая скорость вращения подвижной системы отсчета
параллельна относительной скорости ω
• относительная скорость точки равна нулю
Модуль ускорения Кориолиса равен
ac 2 v r sin
2.1.
ОПРЕДЕЛЕНИЕ
ССС
6.6.
КИНЕМАТИКА
ДВИЖЕНИЯ
ТОЧКИ ОТНОСИТЕЛЬНО НСО
СВОБОДНЫЕ
ЗАТУХАЮЩИЕ
КОЛЕБАНИЯ
29

34. 6.7. УРАВНЕНИЕ НЬЮТОНА ОТНОСИТЕЛЬНО НСО

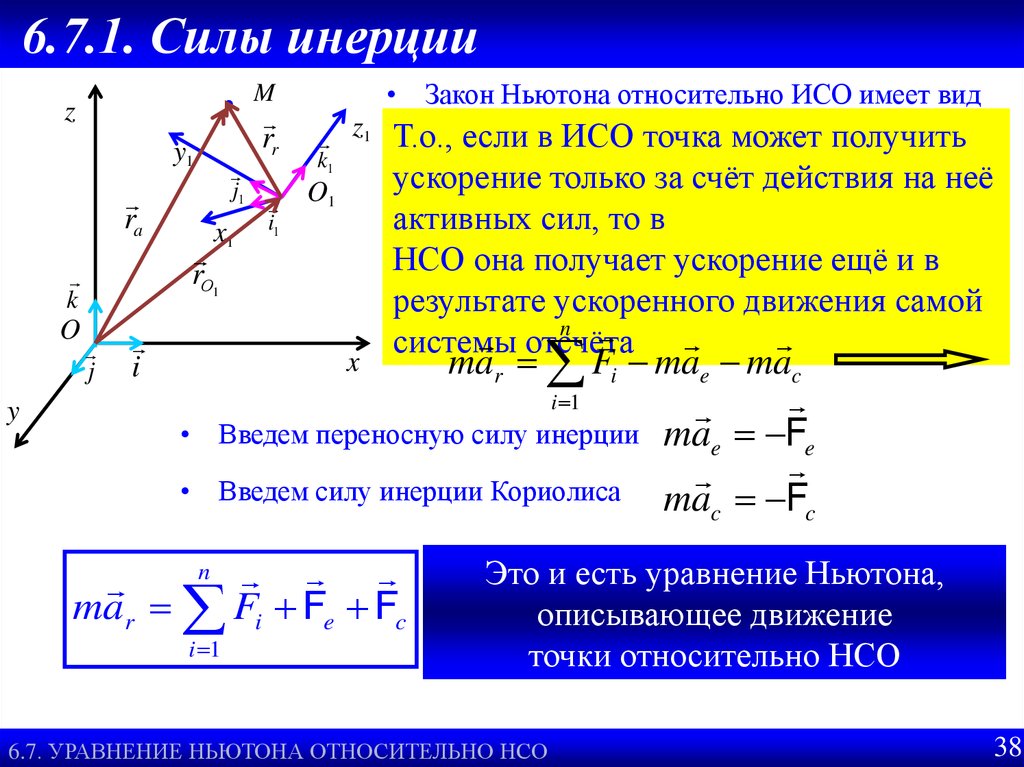
35. 6.7.1. Силы инерции

z
rr
y1
ra
y
j
j1
x1
i1
k1
O1
z1 Т.о., еслиnв ИСО
точка
может
получить
ac неё
maa только
Fi , нозаaсчёт
a a
e ar на
ускорение
действия
i
mar Fi mae mac
i 1
Введем переносную силу инерции mae Fe
Введем силу инерции Кориолиса ma F
c
c
x
активныхi 1сил, то в
n
НСО m
она
aeполучает
Fi ещё и в
ar ac ускорение
результате ускоренногоi движения
самой
1
n
отсчёта
системы
rО1
k
O
• Закон Ньютона относительно ИСО имеет вид
M
n
mar Fi Fe Fc
i 1
Это и есть уравнение Ньютона,
описывающее движение
точки относительно НСО
2.1.
ОПРЕДЕЛЕНИЕ
ССС
6.7.
УРАВНЕНИЕ
НЬЮТОНА
ОТНОСИТЕЛЬНО
НСО
СВОБОДНЫЕ
ЗАТУХАЮЩИЕ
КОЛЕБАНИЯ
38

36. 6.7.2. Природа сил инерции

Обычные силы являются результатом взаимодействия
тел между собой
Они определяются соответствующими физическими
законами и не зависят от выбора СО
Переносная и кориолисова силы инерции, наоборот,
полностью определяются выбором СО
Они в различных неинерциальных системах отсчета
разные
Движение с постоянным ускорением эквивалентно
однородному гравитационному полю
Принцип эквивалентности Эйнштейна
2.1.
ОПРЕДЕЛЕНИЕ
ССС
14.5.
УРАВНЕНИЕ
НЬЮТОНА
ОТНОСИТЕЛЬНО
НСО
СВОБОДНЫЕ
ЗАТУХАЮЩИЕ
КОЛЕБАНИЯ
31

37.

6.7.3. Закон Бэра
• Пусть тело (точка) движется по поверхности Земли в северном полушарии
вдоль меридиана на север
• Ускорение Кориолиса направлено по касательной
N v
r
ωe
ac
R
φ
ac
e
к параллели
Fc
e
S
Бэр Карл Максимович
1792-1876
• Сила Кориолиса направлена противоположно
• Эта сила вызовет отклонение точки вдоль касательной
к параллели вправо от направления её движения
• Т.о., в северном полушарии тело, движущееся
вд ол ь м е р и д и а н а , в с л е д с т в и е в р а щ е н и я
Земли отклоняется вправо от направления
движения
• В Южном полушарии отклонение происходит
влево
• Этим объясняется тот факт, что реки, текущие в
северном полушарии, подмывают правый берег,
а в южном – левый
2.1.
ОПРЕДЕЛЕНИЕ
ССС
6.7.
КИНЕМАТИКА
ДВИЖЕНИЯ
ТОЧКИ ОТНОСИТЕЛЬНО НСО
СВОБОДНЫЕ
ЗАТУХАЮЩИЕ
КОЛЕБАНИЯ
32

38. 6.8. НЕВЕСОМОСТЬ

39.

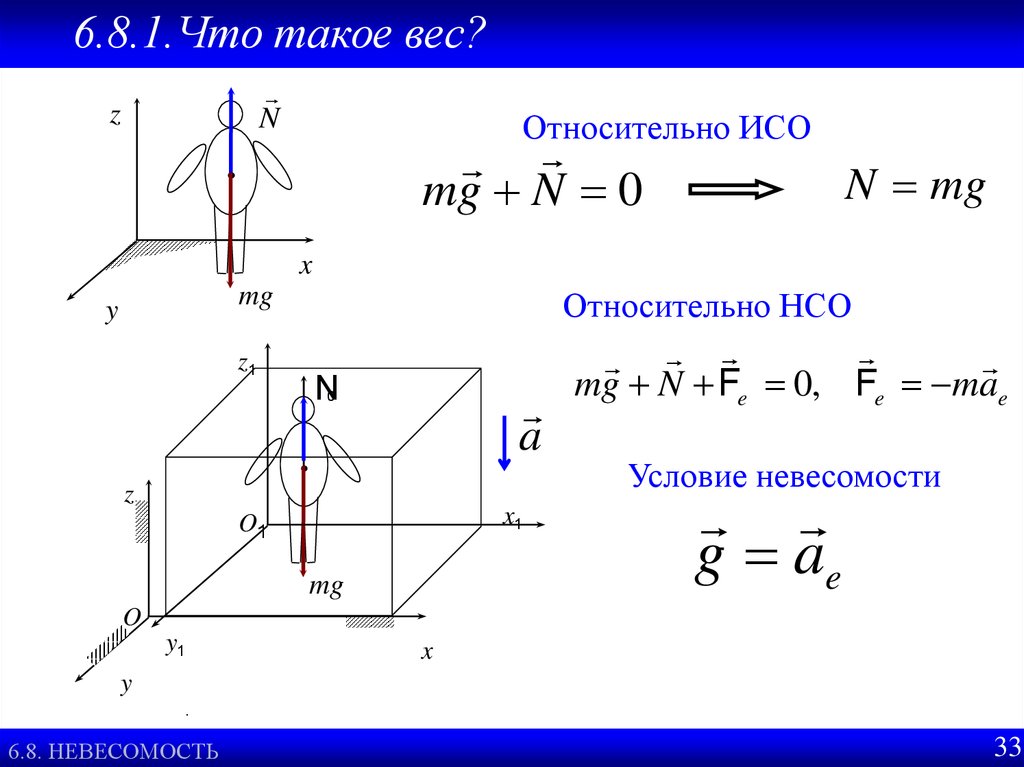
6.8.1.Что такое вес?
N
z
Относительно ИСО
mg N 0
N mg
x
mg
y
z1
Относительно НСО
N0
a
z
x1
O1
mg
mg N Fe 0, Fe mae
Условие невесомости
g ae
O
y1
x
y
.
2.1.
ОПРЕДЕЛЕНИЕ
ССС
6.8.
НЕВЕСОМОСТЬ
СВОБОДНЫЕ
ЗАТУХАЮЩИЕ
КОЛЕБАНИЯ
33

40.

6.8.2. Когда же космонавты будут невесомыми?
2.1.
ОПРЕДЕЛЕНИЕ
ССС
6.8.
НЕВЕСОМОСТЬ
СВОБОДНЫЕ
ЗАТУХАЮЩИЕ
КОЛЕБАНИЯ
34

41.

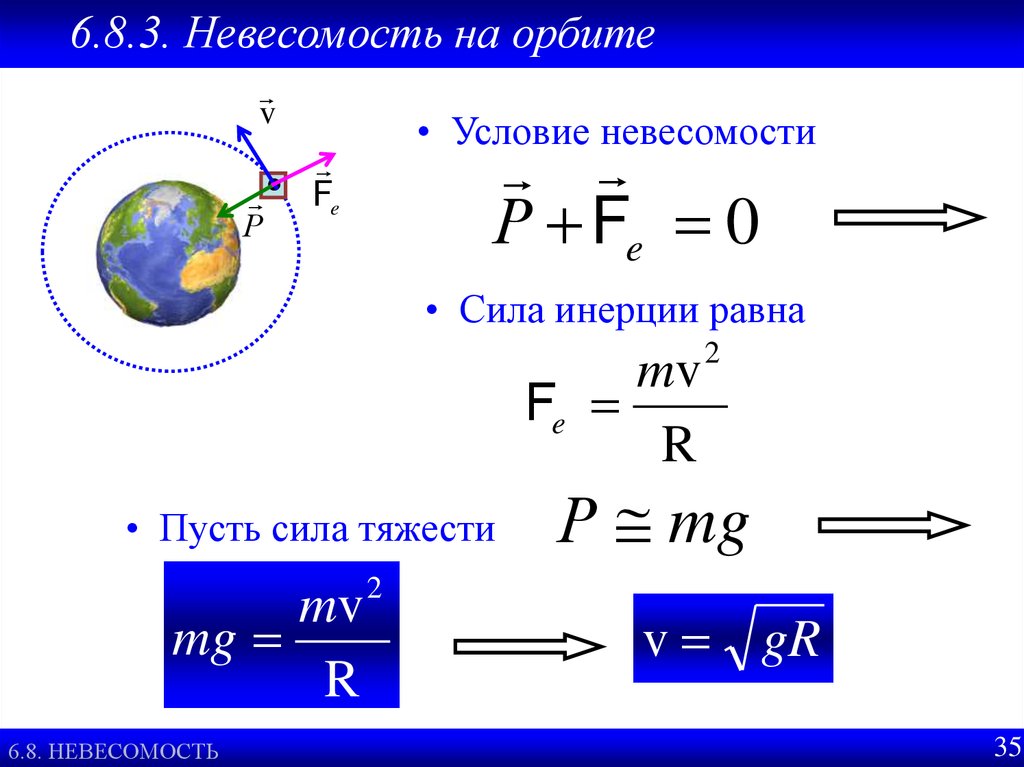
6.8.3. Невесомость на орбите
v
Р
• Условие невесомости
Р Fe 0
Fe
• Сила инерции равна
mv
Fe
R
• Пусть сила тяжести
mv
mg
R
2
2.1.
ОПРЕДЕЛЕНИЕ
ССС
6.8.
НЕВЕСОМОСТЬ
СВОБОДНЫЕ
ЗАТУХАЮЩИЕ
КОЛЕБАНИЯ
2
Р mg
v gR
35

42. 6.9. После лекции

Жди
Ждименя,
меня,иияявернусь,
вернусь.
Всем
Только
смертям
очень жди,
назло.
Кто
Жди,
некогда
ждалнаводят
меня, тот
грусть
пусть
Скажет:
Желтые- дожди,
Повезло.
Не
Жди,
понять,
когдане
снега
ждавшим
метут, им,
Как
Жди,
среди
когда
огня
жара,
Ожиданием
Жди, когда других
своим не ждут,
Ты
Позабыв
спаславчера.
меня.
Как
Жди,
я выжил,
когда избудем
дальних
знать
мест
Только
Писем мы
не придет,
с тобой,
-Просто
Жди, когда
ты умела
уж надоест
ждать,
-Как
Всем,
никто
кто вместе
другой. ждет.
Константин Михайлович Симонов
Симонов К.М.
1915-1979
6.9.ОСНОВНЫЕ
ЗАКЛЮЧЕНИЕ
ЗАКЛЮЧЕНИЕ
1.2.
ПОНЯТИЯ И МОДЕЛИ
36