Similar presentations:
Кинематика. Лекция № 1
1. Кинематика
Кинематикой называют раздел механики вкотором
изучаютгеометрические
свойства
движения тел без учета их инертности (массы)
и действующих на них сил
Кинематика точки
(точка тело, не имеющее размеров и массы)
Основной задачей кинематики точки является
отыскание траектории, скорости и ускорения (при
известном законе движения точки)
2.
Траектория точкиГеометрическое место положений движущейся
точки называется ее траекторией движения.(движение
происходит во времени и в пространстве)
А) Прямолинейное движение
Б) Криволинейное движение
→
V
→
V
М
Траектория
- прямая
М
Траектория
- кривая
→
V - вектор скорости точки М, [м/с]
Примечание: вектор скорости точки
касательной к траектории ее движения.
всегда
направлен
по
3. Три способа задания движения точки
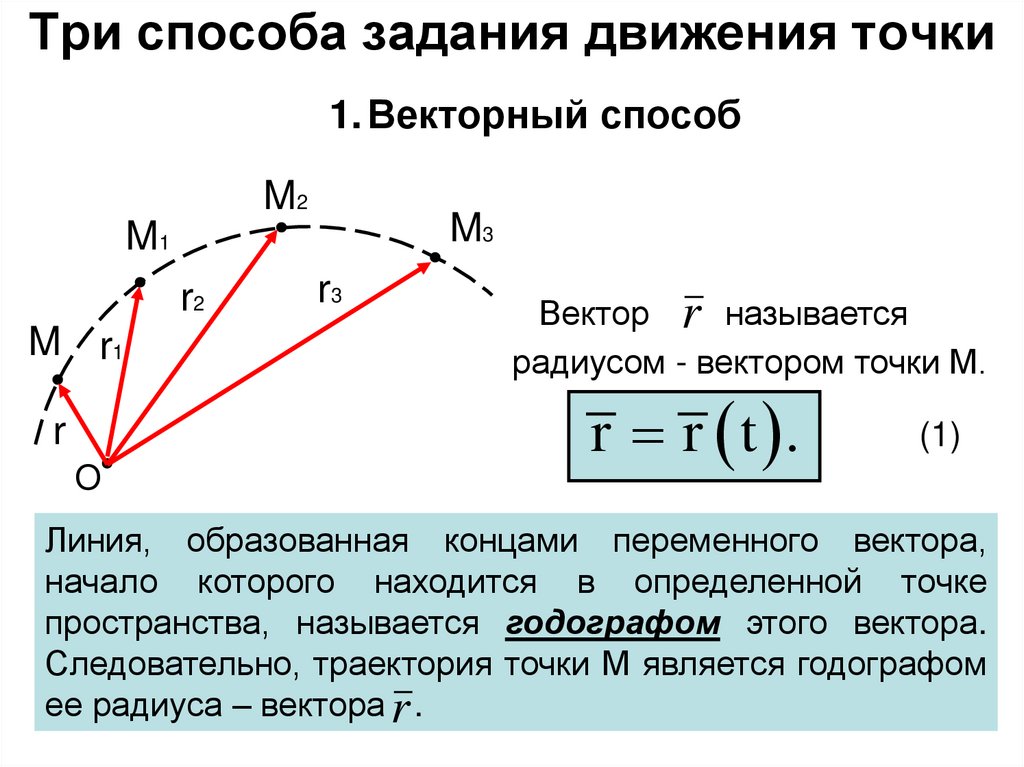
1. Векторный способM2
M3
M1
r2
M r1
r
O
r3
Вектор r называется
радиусом - вектором точки М.
r r t .
(1)
Линия, образованная концами переменного вектора,
начало которого находится в определенной точке
пространства, называется годографом этого вектора.
Следовательно, траектория точки М является годографом
ее радиуса – вектора r .
4. 2. Координатный способ
x = x(t)y = y(t)
z = z(t)
z
M(x,y,z)
r
k
z
j
о
i
x
x
y
y
(2)
Уравнения
(2)
называются
уравнениями движения точки в
декартовых координатах (параметрические уравнения траектории точки)
r i x j y k z
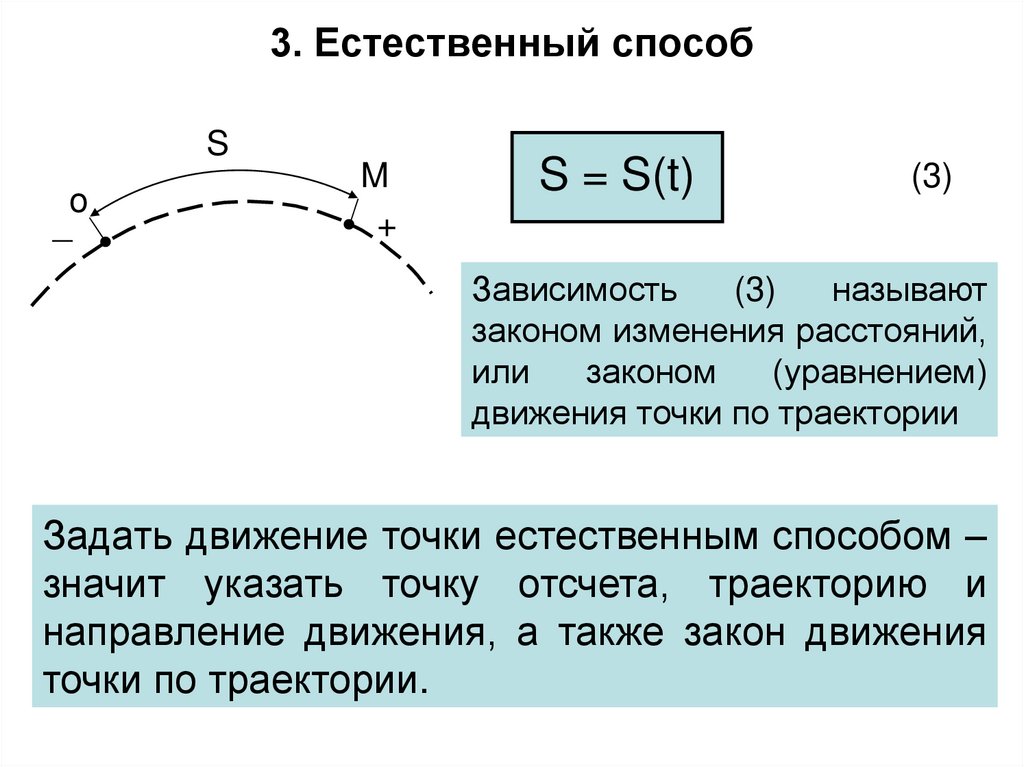
5. 3. Естественный способ
So
_
M
+
S = S(t)
(3)
Зависимость
(3)
называют
законом изменения расстояний,
или
законом
(уравнением)
движения точки по траектории
Задать движение точки естественным способом –
значит указать точку отсчета, траекторию и
направление движения, а также закон движения
точки по траектории.
6. Скорость точки
• Скорость – это векторная величина,характеризующая быстроту изменения
радиуса-вектора движущейся точки
ОБОЗНАЧЕНИЕ:
→
V
РАЗМЕРНОСТЬ в СИ:
[м/c]
НАПРАВЛЕНИЕ: по касательной к траектории
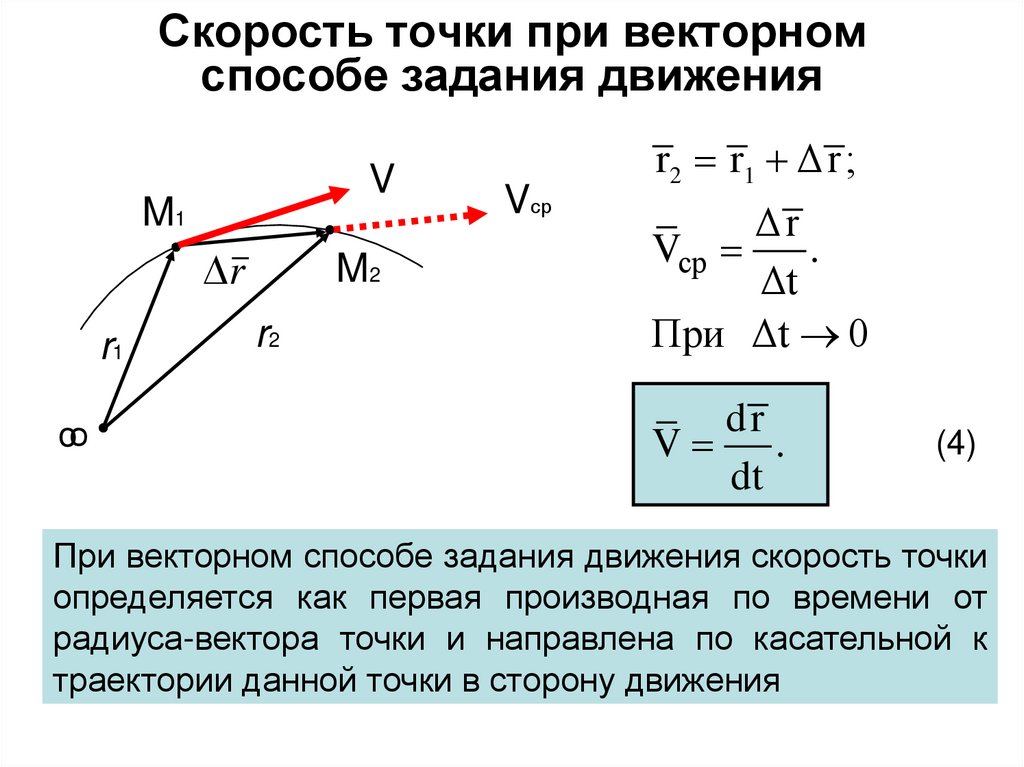
7. Скорость точки при векторном способе задания движения
VM1
r
r1
oо
M2
r2
Vср
r2 r1 Δr ;
Δr
Vср
.
Δt
При Δt 0
dr
V .
dt
(4)
При векторном способе задания движения скорость точки
определяется как первая производная по времени от
радиуса-вектора точки и направлена по касательной к
траектории данной точки в сторону движения
8. Скорость точки при координатном способе задания движения
Пусть движение точки задано в декартовых координатахуравнениями: x = x(t); y = y(t); z = z(t).
Векторное уравнение движения точки:
r ix jy kz ix t jy t kz t , ò î ãäà
dr
dx
dy
dz
V
i
j
k
ix jy kz.
dt
dt
dt
dt
x Vx ; y Vy ; z Vz ;
V
2
2
2
Vx +Vy +Vz .
(5)
При координатном способе задания движения скорость
точки определяется по своим проекциям Vx, Vy, Vz на оси
координат, каждая из которых находится как первая
производная по времени от соответствующей координаты.
9.
Скорость точки должна быть всегда направлена покасательной к траектории в данной точке
Направление вектора скорости может
определено по направляющим косинусам:
z
V
o
x
Vz
Vy
y
Vx
быть
также
Vx
x
cos α
;
V
V
Vy
y
cosβ
;
V
V
Vz
z
cos γ
.
V
V
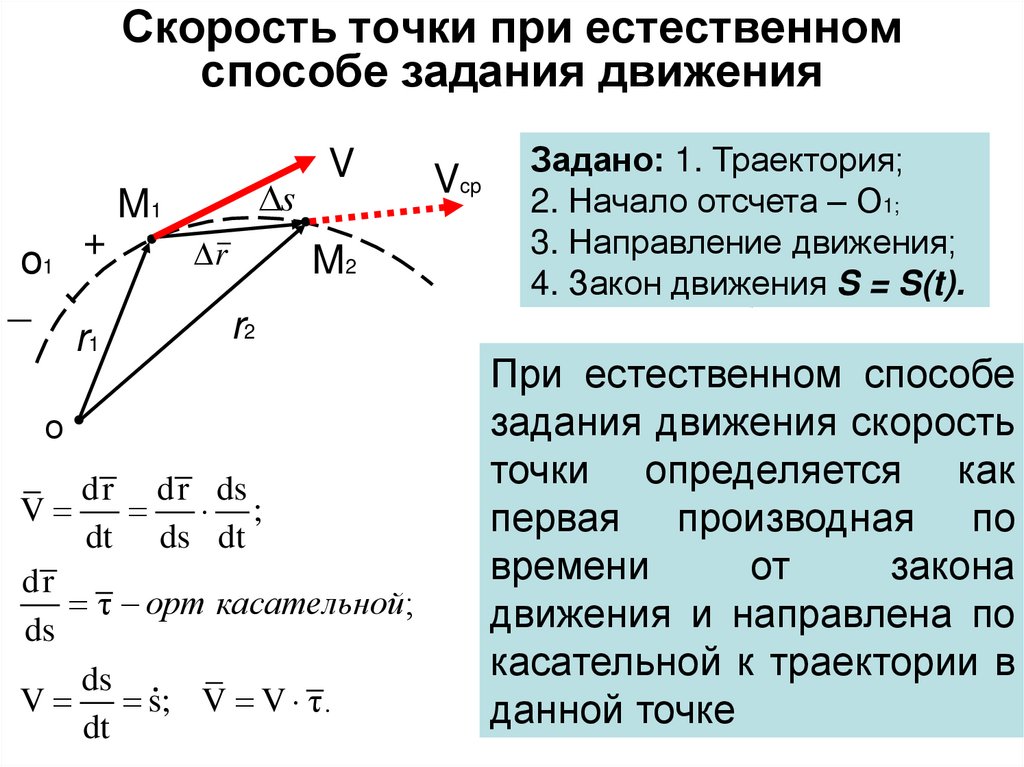
10. Скорость точки при естественном способе задания движения
о1_
+
r1
s
M1
r
V
M2
r2
о
dr dr ds
V
;
dt ds dt
dr
τ орт касательной;
ds
ds
V s; V V τ.
dt
Vcp
Задано: 1. Траектория;
2. Начало отсчета – О1;
3. Направление движения;
4. Закон движения
S = S(t).
s
При естественном способе
задания движения скорость
точки определяется как
первая производная по
времени
от
закона
движения и направлена по
касательной к траектории в
данной точке
11. Ускорение точки
Векторная величина, характеризующая быстротуизменения скорости и по модулю и по направлению, называется ускорением.
ОБОЗНАЧЕНИЕ:
a
РАЗМЕРНОСТЬ в СИ:
[м/c2]
НАПРАВЛЕНИЕ: в сторону вогнутости траектории
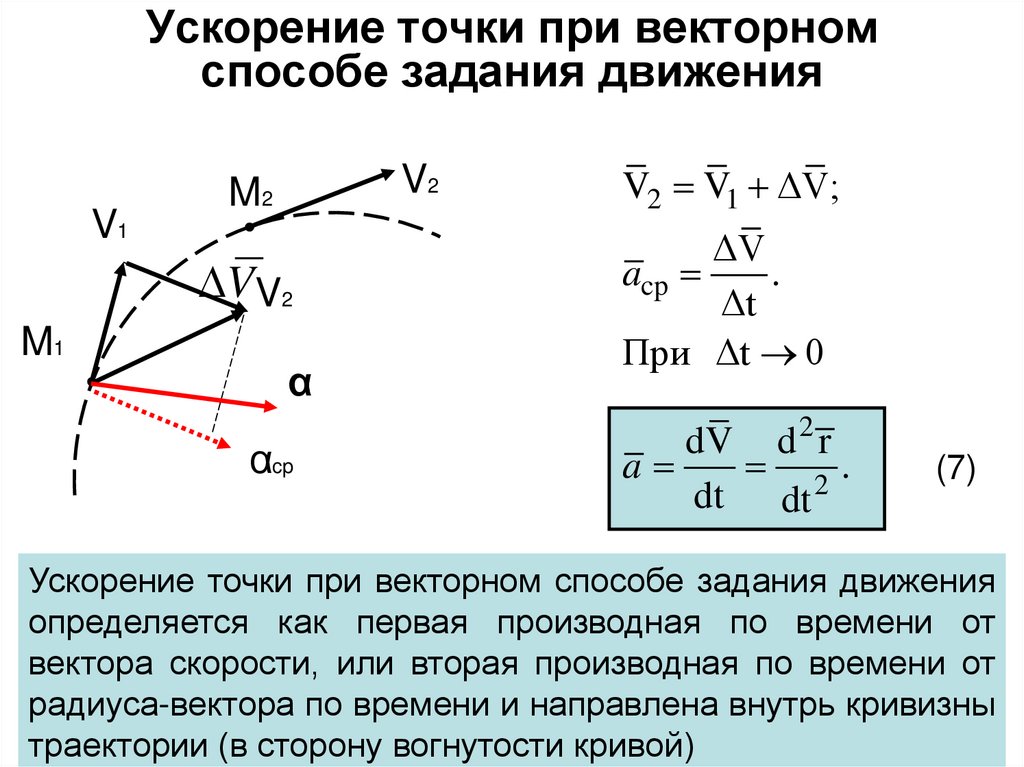
12. Ускорение точки при векторном способе задания движения
V1V2
M2
VV2
M1
α
αcp
V2 V1 ΔV;
ΔV
acp
.
Δt
При Δt 0
dV d 2 r
a
2.
dt dt
(7)
Ускорение точки при векторном способе задания движения
определяется как первая производная по времени от
вектора скорости, или вторая производная по времени от
радиуса-вектора по времени и направлена внутрь кривизны
траектории (в сторону вогнутости кривой)
13. Ускорение точки при координатном способе задания движения
Пусть движение точки задано в декартовых координатахуравнениями: x = x(t); y = y(t); z = z(t).
Векторное уравнение движения точки:
r ix jy kz ix t jy t kz t , тогда
a
d2 r
dt
2
i
d2x
dt
2
j
d2y
dt
2
k
d 2z
dt
2
ix jy kz.
x ax ; y a y ; z az ; a ax2 a 2y az2 .
(8)
При координатном способе задания движения ускорение
точки определяется по своим проекциям на оси координат,
каждая из которых находится как вторая производная
соответствующей координаты по времени
14.
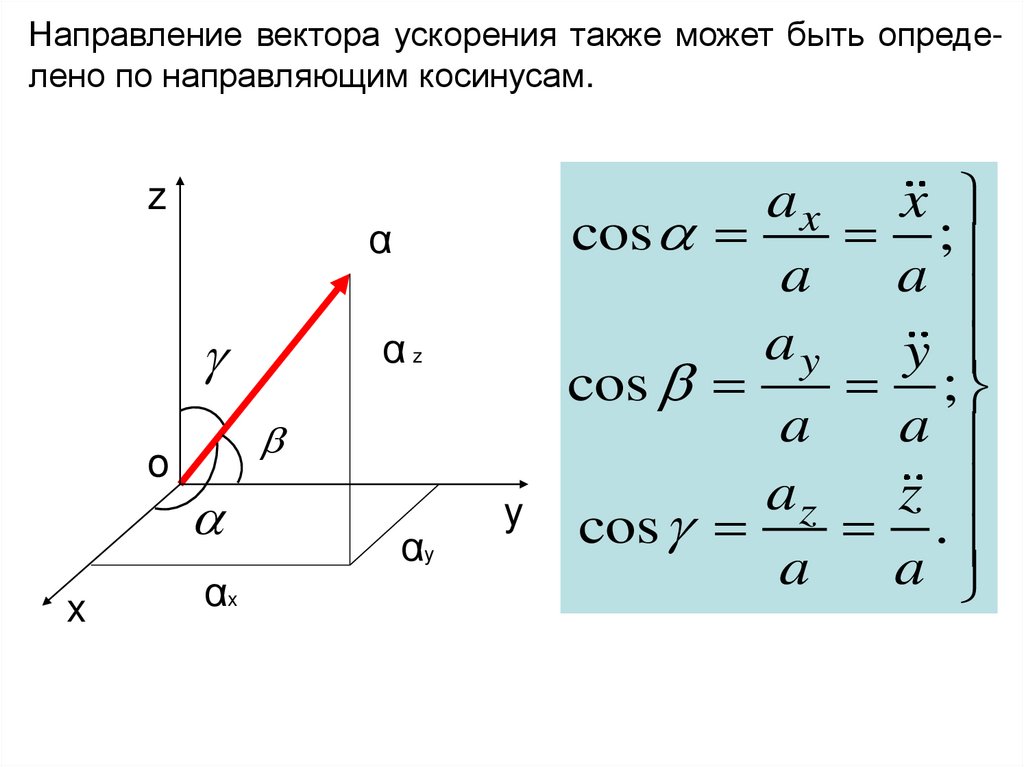
Направление вектора ускорения также может быть определено по направляющим косинусам.z
α
o
x
αz
αx
αy
y
ax
x
cos
;
a
a
ay
y
cos
;
a
a
az
z
cos
.
a
a
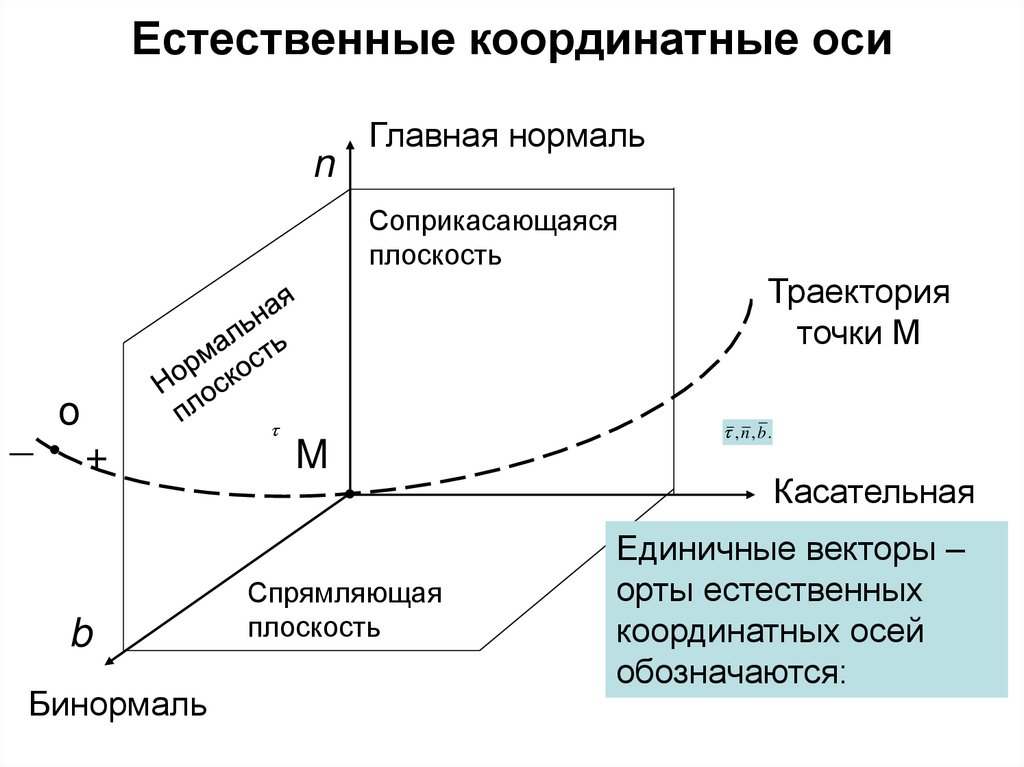
15. Естественные координатные оси
nГлавная нормаль
Соприкасающаяся
плоскость
Траектория
точки М
_
o
+
b
Бинормаль
M
Спрямляющая
плоскость
, n,b.
Касательная
Единичные векторы –
орты естественных
координатных осей
обозначаются:
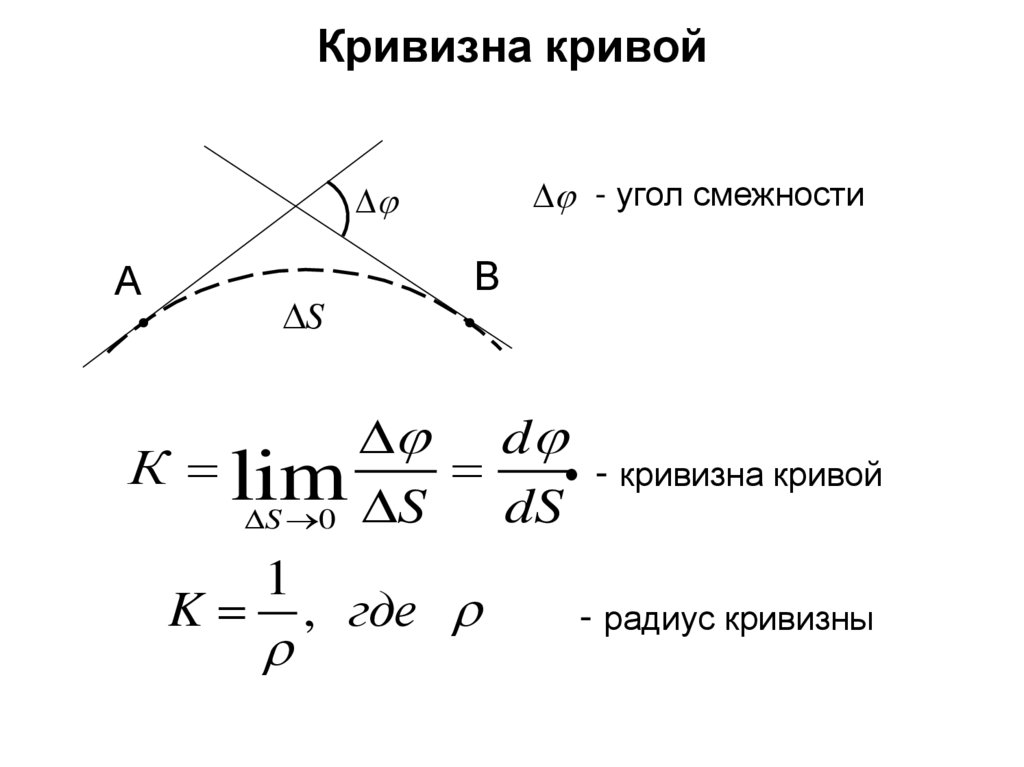
16.
Кривизна кривой- угол смежности
А
S
В
d
К lim
• - кривизна кривой
dS
S 0 S
1
K , где
- радиус кривизны
17. Кривизна кривой
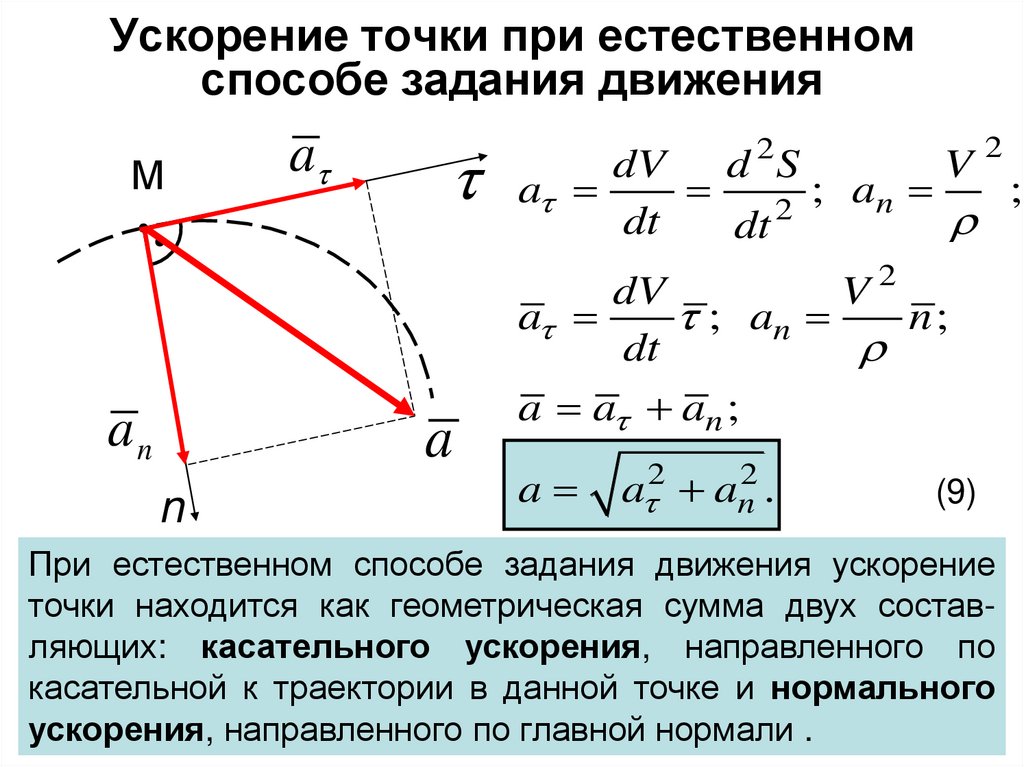
Ускорение точки при естественномспособе задания движения
М
an
a
a
n
2
2
dV
d S
V
a
; an
;
2
dt
dt
dV
V2
a
; an
n;
dt
a a an ;
a
a 2 an2 .
(9)
При естественном способе задания движения ускорение
точки находится как геометрическая сумма двух составляющих: касательного ускорения, направленного по
касательной к траектории в данной точке и нормального
ускорения, направленного по главной нормали .
18. Ускорение точки при естественном способе задания движения
Законы равнопеременного движения точки(a const )









 physics
physics








