Similar presentations:
Уравнение sint = a. Определение синуса
1. Уравнение sint = a
2. Определение синуса
yM(t)
Если точка М числовой окружности
соответствует числу t, то ординату
этой точки называют синусом числа
t и обозначают sin t.
sin t
cos t
0
x
Если M ( t) = M ( x;y), то
y = sin t
3.
Уравнение sin t = ay
Уравнение sin t = a
1
имеет решение
при
0
x
a
-1
Пример: sin t 2
2 1;1
Ответ: решений нет
a 1;1
4. sin t = a, a > 0
sin t = a, a > 0y
P
AM = PC
M
a
AP = AC - PC
C
A
0
0
x
Так как
АМ = arcsin a
AC =
AM:
t1 arcsin a 2 n, n Z
AP:
t2 arcsin a 2 n, n Z
5. sin t = a, a < 0
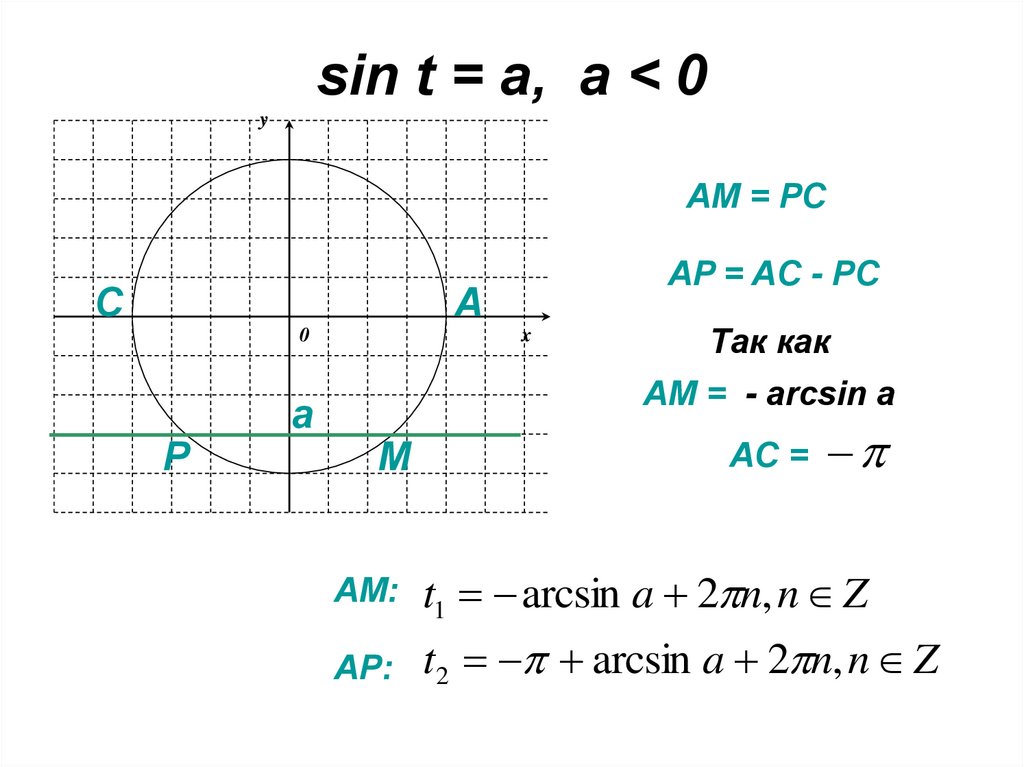
sin t = a, a < 0y
AM = PC
C
AP = AC - PC
A
0
x
АМ = - arcsin a
a
P
Так как
M
AC =
AM:
t1 arcsin a 2 n, n Z
AP:
t2 arcsin a 2 n, n Z
6. Общая формула уравнения sin t = a
t1 arcsin a 2 n, n Zt1 arcsin a 2 n, n Z
t2 arcsin a 2 n, n Z
t2 arcsin a 2 n, n Z
t 1 arcsin a k , k Z
k
при k = 2n
t 1 arcsin a 2n, k Z
2n
t 1 arcsin a 2 n, n Z
при k = 2n +1
t 1
2 n 1
arcsin a (2n 1)
t 1 arcsin a 2 n
t arcsin a 2 n, n Z
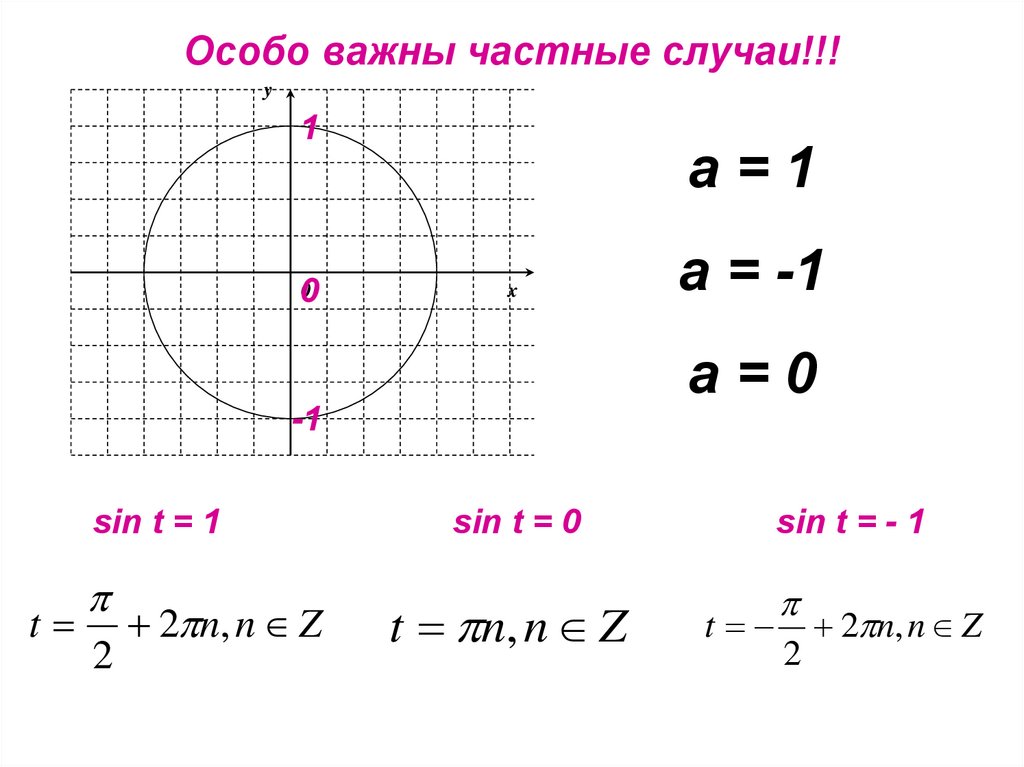
7. Особо важны частные случаи!!!
y1
0
0
а=1
x
а = -1
а=0
-1
sin t = 1
t
2
2 n, n Z
sin t = 0
t n, n Z
sin t = - 1
t
2
2 n, n Z
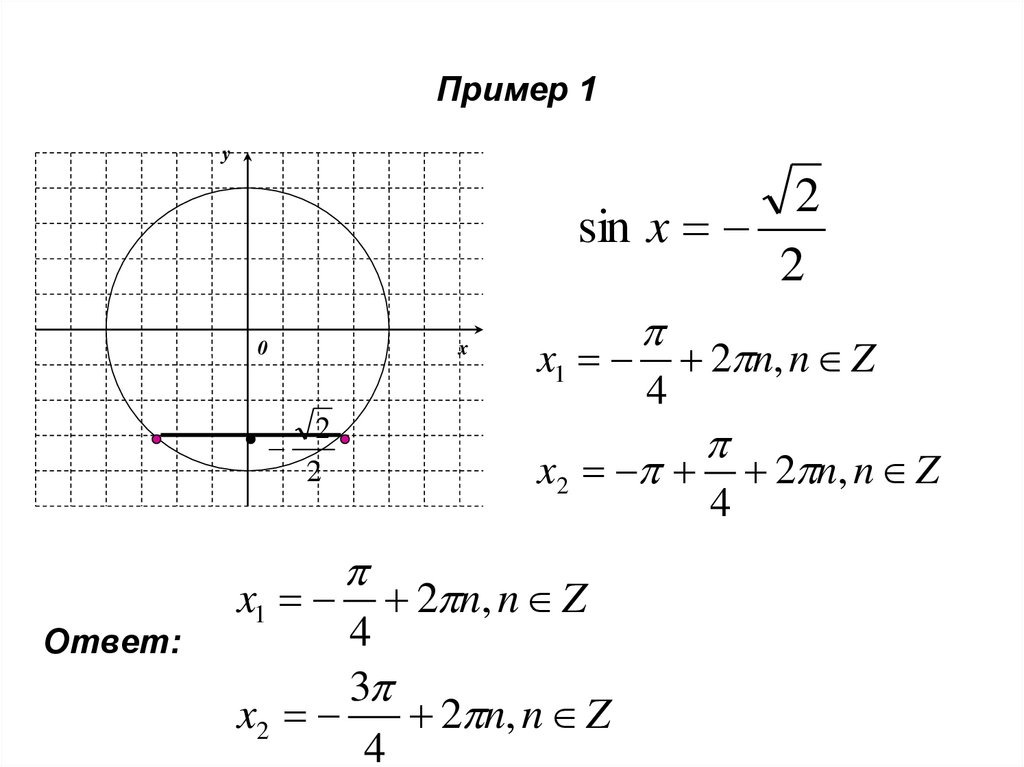
8. Пример 1
y2
sin x
2
0
x
Ответ:
2
2
x1
x1
4
2 n, n Z
x2
2 n, n Z
4
3
x2
2 n, n Z
4
4
2 n, n Z
9. №23.9 в)
4 sin 2 x 3 sin x 0Вынесем общий множитель sin x за скобку
sin x 0
x n, n Z
sin x 4 sin x 3 0
или
4 sin x 3 0
4 sin x 3
3
sin x
4
3
x1 arcsin 2 n, n Z
4
3
x2 arcsin 2 n, n Z
4
10. Домашнее задание
• №23.6 - №23.8• № 23.9 а)б)
• № 23.10







 mathematics
mathematics








