Similar presentations:
Решение простейших тригонометрических уравнений. Решение уравнения cos t = a
1.
Решение простейшихтригонометрических
уравнений
Автор: Лагодич Н.В.
2. Решение уравнения cos t = a
cos t = 0.53. Решение уравнения cos t = a
cos t = 0.5t
3
2 k , k Z
4. Решение уравнения cos t = a
cos t = 0.5t
t
2 k , k Z
3
5
3
2 k , k Z
5. Решение уравнения cos t = a
cos t = 0.5t
t
2 k , k Z
3
5
3
t
2 k , k Z
3
2 k , k Z
6. Решение уравнения cos t = a
cos t = 0.5t
3
2 k , k Z
7. Решение уравнения cos t = a
cos t = 0.48. Решение уравнения cos t = a
cos t = 0.42
t arccos 2 n, n Z
5
9. Решение уравнения cos t = a
cos t = 0.42
t arccos 2 n, n Z
5
2
t arccos 2 n, n Z
5
10. Решение уравнения cos t = a
cos t = 0.42
t arccos 2 n, n Z
5
2
t arccos 2 n, n Z
5
Если cos t = 0.4 то
2
t arccos 2 n, n Z
5
11. Решение уравнения cos t = a
cos t = a12. Решение уравнения cos t = a
Общая формула длярешения уравнений
вида:
cos t = a
t arccos a 2 n, n Z
13. Решение уравнения sin t = a
3sin x
2
14. Решение уравнения sin t = a
3sin x
2
х 2 n, n Z
3
15. Решение уравнения sin t = a
3sin x
2
х 2 n, n Z
3
2
х
2 n, n Z
3
16. Решение уравнения sin t = a
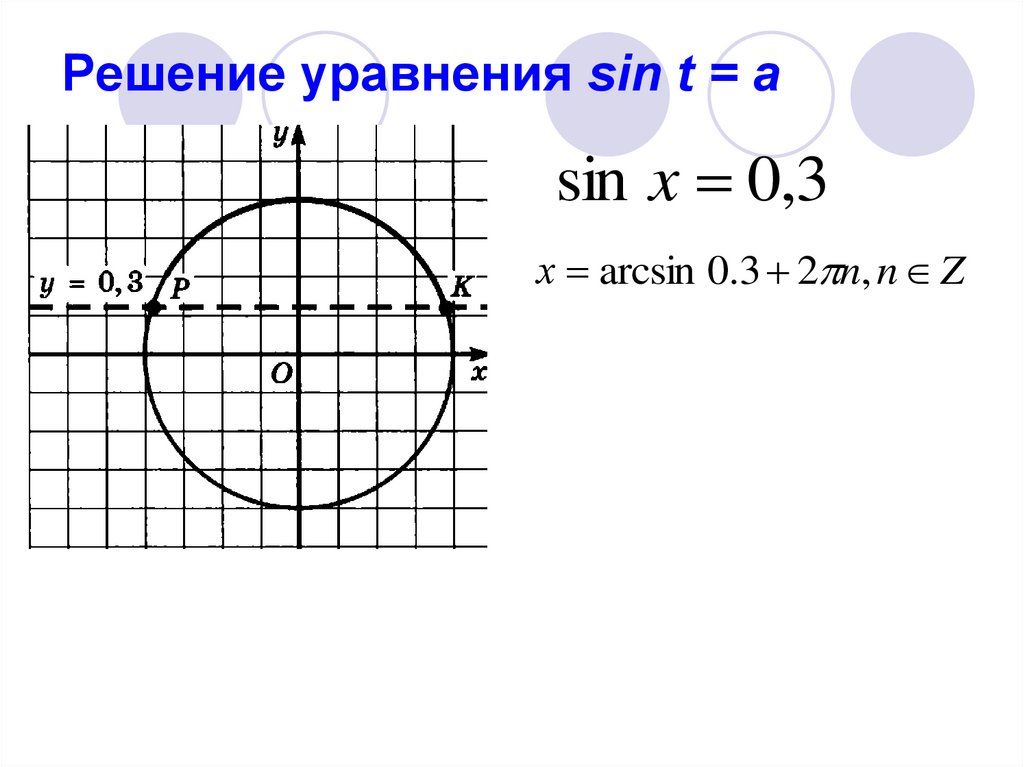
sin x 0,317. Решение уравнения sin t = a
sin x 0,3х arcsin 0.3 2 n, n Z
18. Решение уравнения sin t = a
sin x 0,3х arcsin 0.3 2 n, n Z
х arcsin 0.3 2 n, n Z
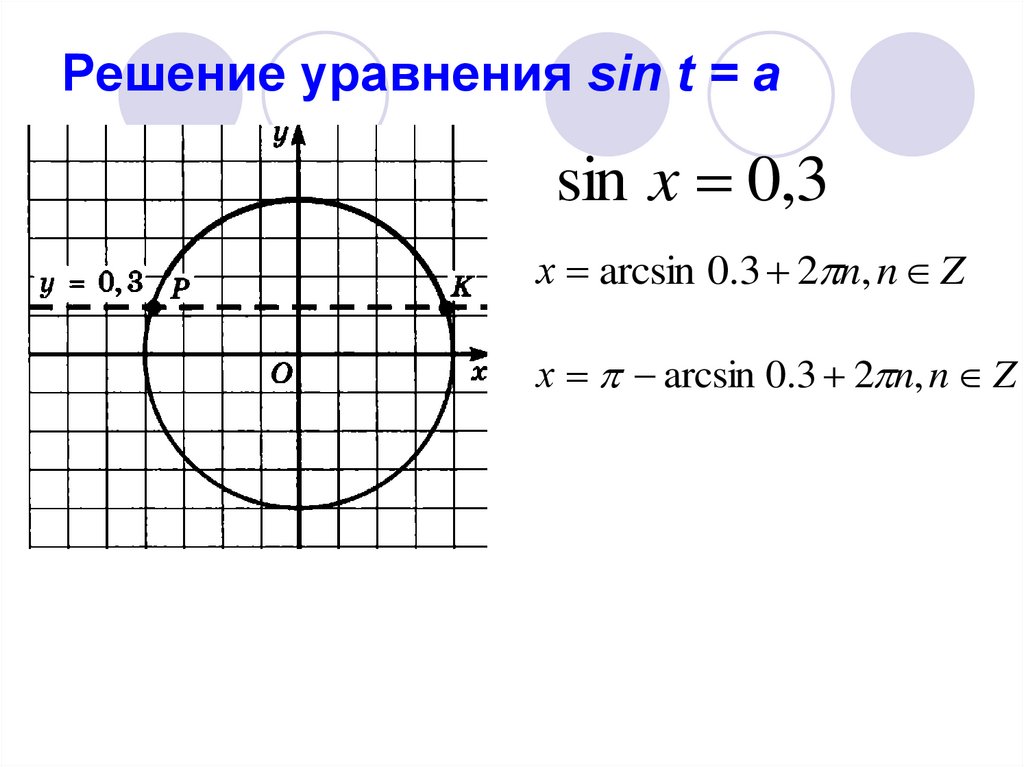
19. Решение уравнения sin t = a
sin x 0,320. Решение уравнения sin t = a
sin x 0,3х arcsin( 0.3) 2 n, n Z
21. Решение уравнения sin t = a
sin x 0,3х arcsin( 0.3) 2 n, n Z
х arcsin 0.3 2 n, n Z
22. Решение уравнения sin t = a
sin x 0,3х arcsin( 0.3) 2 n, n Z
х arcsin 0.3 2 n, n Z
х arcsin 0.3 2 n, n Z
23. Решение уравнения sin t = a
sin x 0,3х arcsin( 0.3) 2 n, n Z
х arcsin 0.3 2 n, n Z
х arcsin 0.3 2n, n Z
х ( arcsin 0.3) 2 n, n Z
24. Решение уравнения sin t = a
sin x 0,3х arcsin 0.3 2 n, n Z
sin x 0,3
х arcsin 0.3 2 n, n Z
х arcsin 0.3 2 n, n Z
х arcsin 0.3 2 n, n Z
25. Решение уравнения sin t = a
а 1Если а 1 , то
уравнение sin t = a
имеет две серии
решений:
26. Решение уравнения sin t = a
а 1Если а 1 , то
уравнение sin t = a
имеет две серии
решений:
х arcsin а 2 n, n Z
27. Решение уравнения sin t = a
а 1Если а 1 , то
уравнение sin t = a
имеет две серии
решений:
х arcsin а 2 n, n Z
х arcsin а 2 n, n Z
28. Решение уравнения sin t = a
- общая формула для решения уравнений вида: sin t = a29. Общие формулы для решения уравнений вида: sin t = a, cos t = a.
sin t = at 1 arcsin a n, n Z
n
cos t = a
t arccos a 2 n, n Z
30. Частные случаи:
cos x 031. Частные случаи:
cos x 0x
2
k , k Z
32. Частные случаи:
cos x 0x
2
k , k Z
sin x 0
33. Частные случаи:
cos x 0x
2
k , k Z
sin x 0
x k , k Z
34. Частные случаи:
cos x 0x
2
k , k Z
cos x 1
sin x 0
x k , k Z
35. Частные случаи:
cos x 0x
2
k , k Z
cos x 1
x 2 k , k Z
sin x 0
x k , k Z
36. Частные случаи:
cos x 0x
2
k , k Z
cos x 1
x 2 k , k Z
sin x 0
x k , k Z
sin x 1
37. Частные случаи:
cos x 0x
2
k , k Z
cos x 1
x 2 k , k Z
sin x 0
x k , k Z
sin x 1
x
2
2 k , k Z
38. Частные случаи:
cos x 0x
2
k , k Z
cos x 1
x 2 k , k Z
cos x 1
sin x 0
x k , k Z
sin x 1
x
2
2 k , k Z
39. Частные случаи:
cos x 0x
2
k , k Z
cos x 1
x 2 k , k Z
cos x 1
x 2 k , k Z
sin x 0
x k , k Z
sin x 1
x
2
2 k , k Z
40. Частные случаи:
cos x 0x
2
k , k Z
cos x 1
x 2 k , k Z
cos x 1
x 2 k , k Z
sin x 0
x k , k Z
sin x 1
x
2
2 k , k Z
sin x 1
41. Частные случаи:
cos x 0x
2
k , k Z
cos x 1
x 2 k , k Z
cos x 1
x 2 k , k Z
sin x 0
x k , k Z
sin x 1
x
2
2 k , k Z
sin x 1
x
2
2 k , k Z
42. Самостоятельная работа
I варианта) cos x 3
2
II
вариант
1
а) sin x
2
cos x 1
б) sin x 1
в) 2 cos x 1
б)
г) sin x 0,7
в) 2 sin x 3
г) cos x 0,3
д) sin x 0,4
д) sin x 0,6








































 mathematics
mathematics








