Решение простейших тригонометрических уравнений

1.

2.

arcsin
sin a
= x
arctg
tg
[-1;1] [- π/2;π/2]
a
(-∞;+∞)
= x
(- π/2;π/2)
2
arccos
cos a
= x
[-1; 1] [0;π]
0
2
arcсtg
сtg a
(-∞;+∞)
= x
(0;π)

3.

Вычислите:
arcsin
3
2
3
arccos (
)
2
arctg
3
3
3
5
6
6
2
arcsin
2
4
arcctg ( 3)
5
6

4.

Найдите ошибку
3
arcsin (-1) =
2
2
arccos (
)=
4
2
arctg
3
arcsin (-1) =
1
5
arcsin ( ) =
2
6
3
arcctg ( ) =
3
3
2
3
2
arccos (
)=
4
2
= 6
arctg
3
= 3
1
arcsin ( ) =
6
2
2
3
arcctg ( ) =
3
3

5.

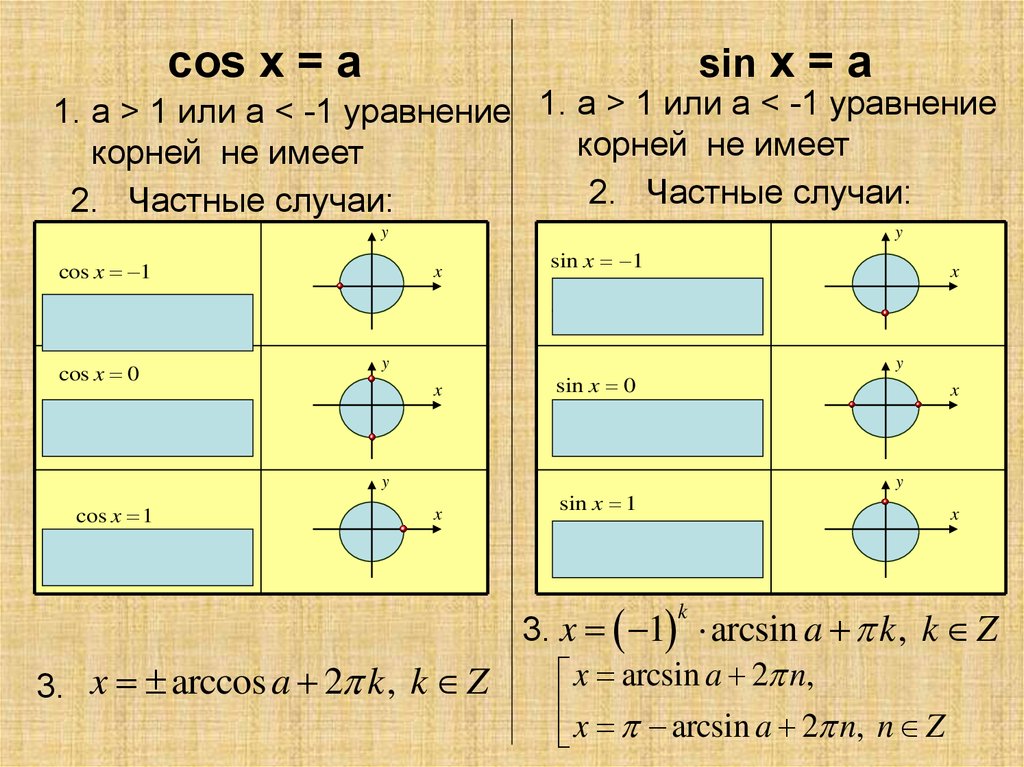
cos x = a
sin x = a
1. a > 1 или a < -1 уравнение 1. a > 1 или a < -1 уравнение
корней не имеет
корней не имеет
2. Частные случаи:
2. Частные случаи:
y
cos x 1
y
x
x 2 n, n Z
cos x 0
x
2
x
y
x
2
x
2 n, n Z
y
sin x 0
x
x n, n Z
n, n Z
y
cos x 1
sin x 1
x
x 2 n, n Z
y
sin x 1
x
2
x
2 n, n Z
3. x 1 arcsin a k , k Z
x arcsin a 2 n,
x arcsin a 2 n, n Z
k
3. x arccos a 2 k , k Z

6.

Решите уравнение:
1). 2 sin x = 1
2).
2 cos x 1
3).
2 sin x 3
4).
cos x 3
5).
sin x 0.1
x ( 1)
k
6
k _ k
3
x
2 n _ n
4
x ( 1)
k 1
3
k _ k
уравнение корней не имеет
x ( 1)
k 1
arcsin 0.1 k _ k

7.

1
6). cos( x )
3
2
6) cos(x+π/3) = ½
x+π/3 = ±arccos1/2 + 2πk, kЄZ
x+π/3 = ±π/3 + 2πk, kЄZ
x = -π/3 ± π/3 + 2πk, kЄZ
Ответ: -π/3 ± π/3 + 2πk, kЄZ

8.

x
7). sin( ) 0
3
3) sin(π – x/3) = 0
упростим по формулам приведения
sin(x/3) = 0
частный случай
x/3 = πk, kЄZ
x = 3πk, kЄZ.
Ответ: 3πk, kЄZ.

9.

Пример.
Решите уравнение 2 cos x 3 0
4
3
Решение. 2 cos x 3, cos x
2
4
4
Учитывая четность косинуса, получим
3
cos x
4
2
Следовательно,
3
5
x arccos
2 k или x
2 k , k Z
4
2
4
6
5
x
2 k , k Z
4
6
5
2 k , k Z
Ответ: x
4
6

10.

1 вариант
2 cos 4x 1 0
1
cos 3x
3
2
2 cos x 0
x
3ctg 3
4
2 вариант
2
cos 2x
2
2
3
sin 4x
0
2
cos( x) 1
x
3tg 1
2