Тригонометрические уравнения

1. Разноуровневый урок по теме «Тригонометрические уравнения»

РАЗНОУРОВНЕВЫЙ УРОК ПО
ТЕМЕ
«ТРИГОНОМЕТРИЧЕСКИЕ
УРАВНЕНИЯ»
Учитель математики
МАОУ СОШ №3
Короткова А. Э.
Г. Курганинск, 2014 г.

2.

Учиться можно только
весело.
Чтобы переваривать
знания, надо поглощать
их с аппетитом.
Анатоль Франс
1844 - 1924

3. Найди ошибку.

НАЙДИ ОШИБКУ.
1
2
arcsin 45
2
2
1 2
arccos
33
2
0
?
3
3
arcsin 3 arcsin 1 3 3
4
4
4
arctg 1 arctg
4 4
5
3
arcctg 3
46

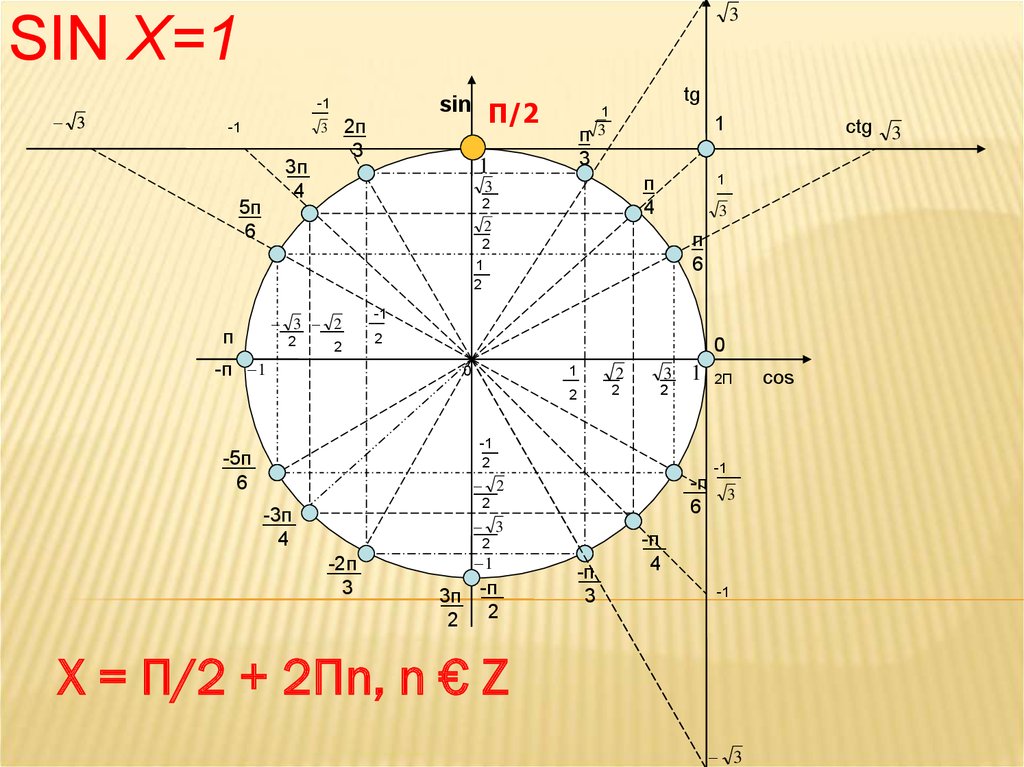
4. Sin x=1

3
SIN X=1
3
sin
-1
__
-1
2п
__
3
3
3п
__
4
5п
__
6
tg
П/2
1
__
1
п3
_
3
1
п
_
4
3
__
2
1
__
3
__2
2
п
_
6
1
__
2
2
___
3 ___
п
2
2
-п 1
-1
__
2
0
0
1
__
2
__2
2
__
3
2
-1
__
2
___
-5п
6
1
__
3п
__ -п
2 2
2П
-1
___
__3
_
2
___
-2п
3
1
-п
__
3
6
__2
_
2
___
-3п
4
ctg 3
-п
__
3
-п
__
4
-1
X = П/2 + 2Пn, n € Z
3
cos

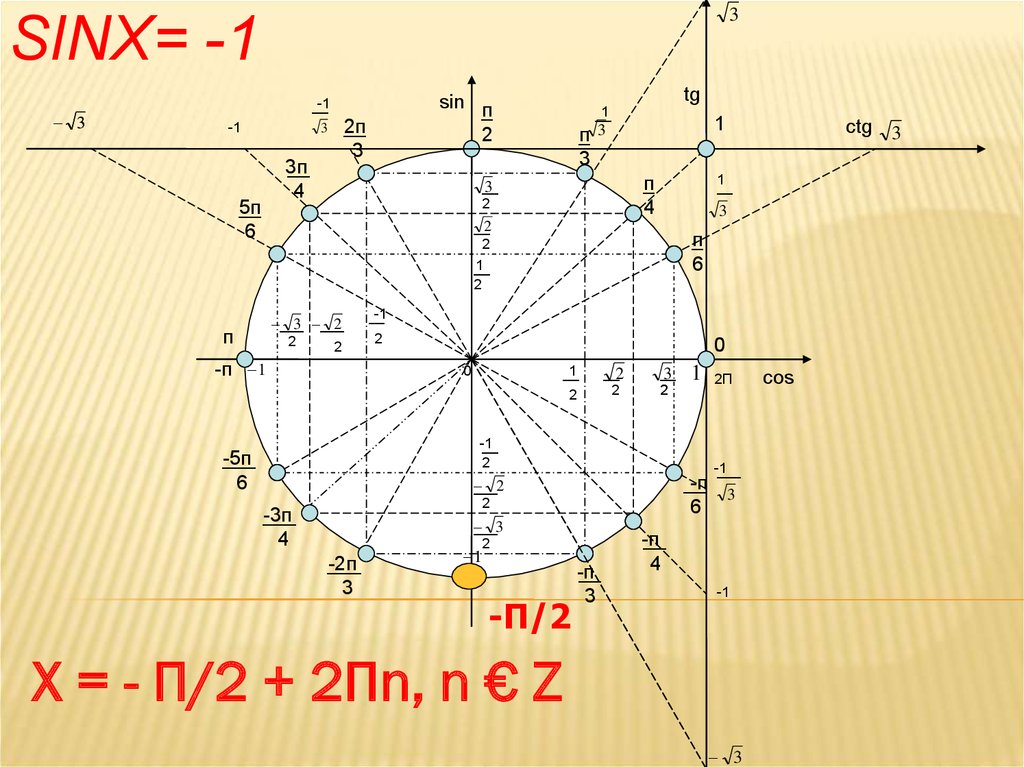
5. Sinx= -1

3
SINX= -1
3
-1
2п
__
3
3
3п
__
4
5п
__
6
tg
sin _
п
2
-1
__
1
__
1
п3
_
3
п
_
4
3
__
2
1
__
3
__2
2
п
_
6
1
__
2
2
___
3 ___
п
2
2
-п 1
-1
__
2
0
0
1
__
2
__2
2
__
3
2
-1
__
2
___
-5п
6
___
-2п
3
-П/2
2П
-1
___
__3
_
2
1
1
-п
__
3
6
__2
_
2
___
-3п
4
ctg 3
-п
__
3
-п
__
4
-1
X = - П/2 + 2Пn, n € Z
3
cos

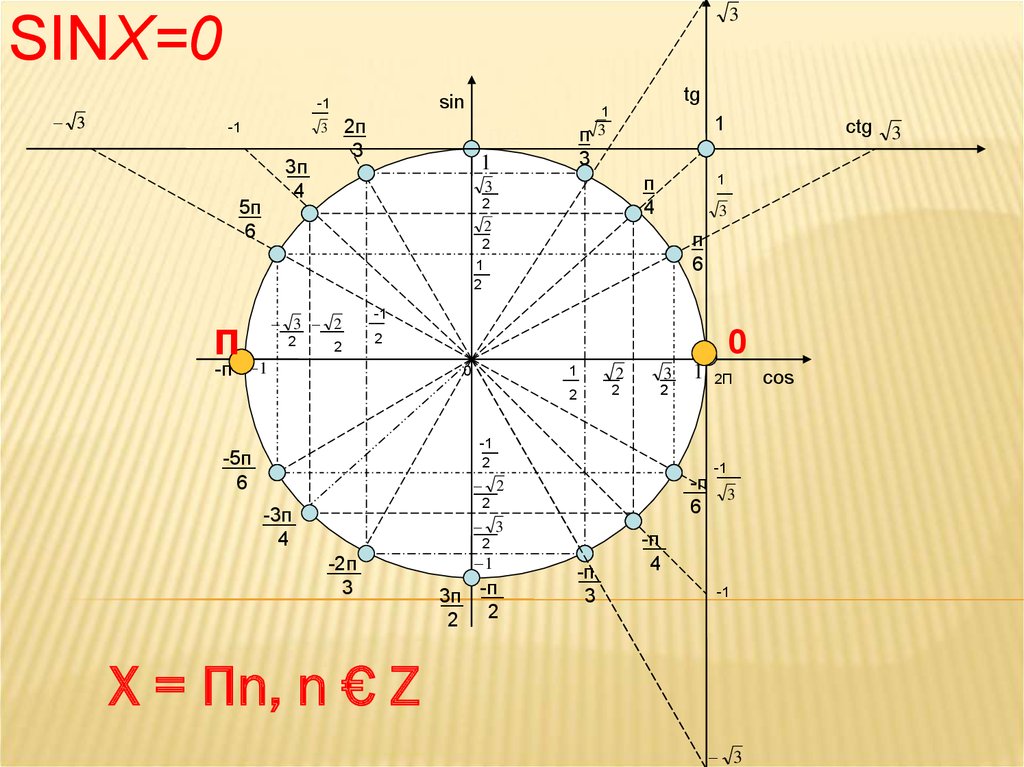
6. Sinx=0

3
SINX=0
3
-1
2п
__
3
3
3п
__
4
5п
__
6
tg
sin
-1
__
1
__
1
п3
_
3
П/2
1
п
_
4
3
__
2
1
__
3
__2
2
п
_
6
1
__
2
П
-п
2
___
3 ___
2
2
ctg 3
-1
__
0
2
1
0
1
__
2
__2
2
__
3
2
-1
__
2
___
-5п
6
-1
___
__3
_
2
___
-2п
3
1
__
3п
__ -п
2 2
2П
-п
__
3
6
__2
_
2
___
-3п
4
1
-п
__
3
-п
__
4
-1
X = Пn, n € Z
3
cos

7. Sinx= a

3
SINX= A
3
-1
tg
sin
-1
__
2п
__
3
3
3п
__
1
__
1
4
fа
5п a
П - aпrcsin
6
3
arcsin
a
_
п
6
1
__
2
2
___
3 ___
П
2
2
-п 1
-1
__
0
2
0
1
__
2
__2
2
__
3
2
-1
__
2
___
-5п
6
1
__
3п
__ -п
2 2
2П
-1
___
__3
_
2
___
-2п
3
1
-п
__
3
6
__2
_
2
___
-3п
4
ctg 3
1
__
3
__
2
2
а __2
__
1
п3
_
3
П/2
-п
__
3
-п
__
4
-1
X =(-1)ⁿarcsin a + Пn, n € Z
3
cos

8. Cos x=1

3
COS X=1
3
-1
2п
__
3
3
3п
__
4
5п
__
6
tg
sin
-1
__
1
__
1
п3
_
3
П/2
1
п
_
4
3
__
2
1
__
3
__2
2
п
_
6
1
__
2
2
___
3 ___
п
2
2
-1
__
0
2
-п 1
0
1
__
2
__2
2
__
3
2
-1
__
2
___
-5п
6
1
__
3п
__ -п
2 2
2П
-1
___
__3
_
2
___
-2п
3
1
-п
__
3
6
__2
_
2
___
-3п
4
ctg 3
-п
__
3
-п
__
4
-1
X = 2Пn, n € Z
3
cos

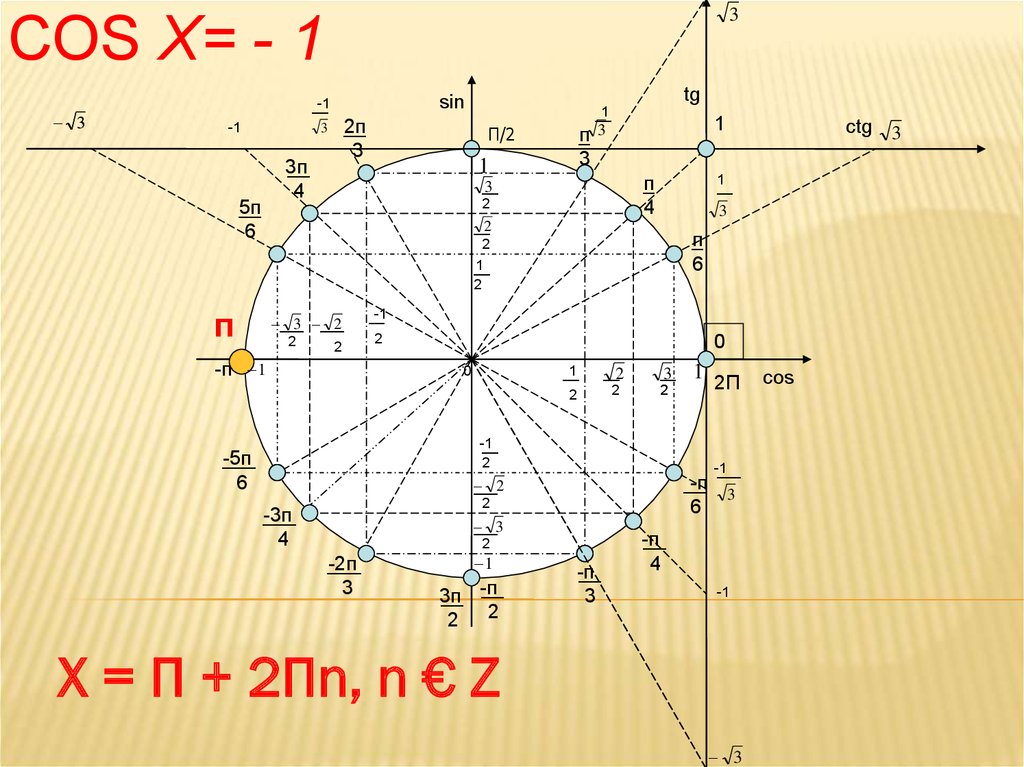
9. Cos x= - 1

3
COS X= - 1
3
-1
2п
__
3
3
3п
__
4
5п
__
6
tg
sin
-1
__
1
__
1
п3
_
3
П/2
1
п
_
4
3
__
2
1
__
3
__2
2
п
_
6
1
__
2
п
2
___
3 ___
2
2
-п 1
-1
__
2
0
0
1
__
2
__2
2
__
3
2
-1
__
2
___
-5п
6
-1
___
__3
_
2
___
-2п
3
1
__
3п
__ -п
2 2
1 2П
-п
__
3
6
__2
_
2
___
-3п
4
ctg 3
-п
__
3
-п
__
4
-1
X = П + 2Пn, n € Z
3
cos

10. Cos x= 0

3
COS X= 0
3
-1
2п
__
3
3
3п
__
4
5п
__
6
tg
П/2
sin
-1
__
1
__
1
п3
_
3
1
п
_
4
3
__
2
1
__
3
__2
2
п
_
6
1
__
2
2
___
3 ___
п
2
2
-1
__
2
0
-п 1
0
1
__
2
__2
2
__
3
2
-1
__
2
___
-5п
6
___
-3п
4
-1
___
__3
_
2
1
3п/2
-
1 2П
-п
__
3
6
__2
_
2
___
-2п
3
ctg 3
-п
__
3
-п
__
4
-1
X = П/2 + Пn, n € Z
3
cos

11. Cos x= a

3
COS X= A
3
-1
2п
__
3
3
3п
__
4
5п
__
6
tg
sin
-1
__
1
__
п3
_
3
П/2
1
3
__
2
1
arccos 1__a
3
__2
2
п
_
6
1
__
2
2
___
3 ___
п
2
2
-1
__
a
2
-п 1
0
1
__
0
__
3
2
__2
2
2
-1
__
2
___
-5п
6
___
-3п
4
__3
_
2
1
-п/2
-
1 2П
-1
___
-п
__
3
6
__2
_
2
___
-2п
3
ctg 3
-п
__
4
- arccos a
-п
__
3
-1
X = ± arccos a + 2 Пn, n € Z
3
cos

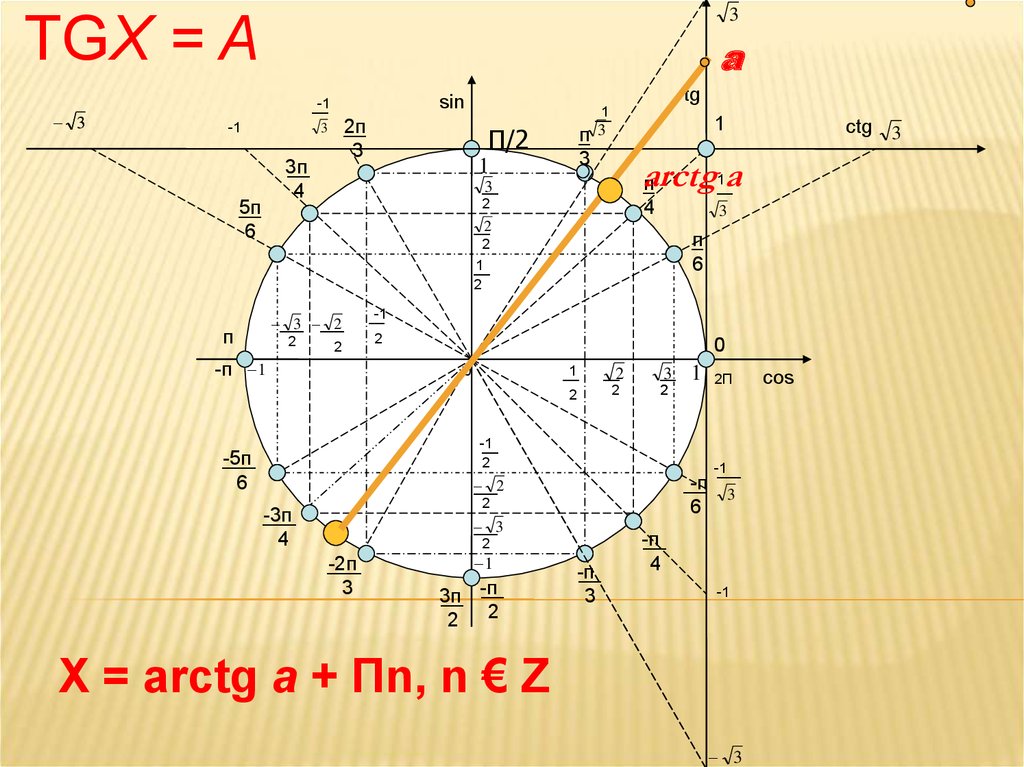
12. tgx = a

3
TGX = A
3
a
-1
2п
__
3
3
3п
__
4
5п
__
6
tg
sin
-1
__
1
__
п3
_
3
П/2
1
1
arctg
a
_
п
1
__
3
__
2
4
3
__2
п
_
6
2
1
__
2
2
___
3 ___
п
2
2
-п 1
-1
__
2
0
0
1
__
2
__2
2
__
3
2
-1
__
2
___
-5п
6
1
__
3п
__ -п
2 2
2П
-1
___
__3
_
2
___
-2п
3
1
-п
__
3
6
__2
_
2
___
-3п
4
ctg 3
-п
__
3
-п
__
4
-1
X = arctg a + Пn, n € Z
3
cos

13. Установите соответствие:

УСТАНОВИТЕ СООТВЕТСТВИЕ:
1
sin x = 0
2
cos x = -1
3
sin x = 1
4
5
6
7
cos x = 1
tg x = 1
sin x = - 1
cos x = 0
2
2 k , k Z
k , k Z
2 k , k Z
2
2
k , k Z
2 k , k Z
2 k , k Z
4
k , k Z

14. Установите соответствие:

УСТАНОВИТЕ СООТВЕТСТВИЕ:
1
sin x = 0
2
cos x = -1
3
sin x = 1
4
5
6
7
cos x = 1
tg x = 1
sin x = - 1
cos x = 0
2
2 k , k Z
k , k Z
2 k , k Z
2
2
k , k Z
2 k , k Z
2 k , k Z
4
k , k Z

15. Уравнения повышенного уровня сложности

УРАВНЕНИЯ ПОВЫШЕННОГО УРОВНЯ
СЛОЖНОСТИ
1. Решить уравнение:
7 sin²x + 4 sinxcosx -3 cos²x = 0.
Указать корни, принадлежащие отрезку
[3П/2; 5П/2 ].
2. Решить уравнение:
(4 sin²x + 16 sinx + 7) lg(cosx) = 0.

16. Решение уравнения №1 повышенный уровень сложности

РЕШЕНИЕ УРАВНЕНИЯ №1
ПОВЫШЕННЫЙ УРОВЕНЬ СЛОЖНОСТИ
3
-1
2п
__
3
3
3п
__
4
5п
__
6
tg
sin п
_5П/2
2
-1
__
1
__
1
п3
_
3
1
п
_
4
3
__
2
3
п
_
6
1
__
2
п
2
2
ctg 3
1
__
__2
2
2
___
3 ___
3
3/7
arctg3/7 +2П
-1
__
2
0
-п 1
0
1
__
2
__2
2
__
2
1
2П cos
3
-1
__
2
___
-5п
6
-1
___
-п
__
3
6
__2
_
2
___
-3п
4
-П/4 + 2П
__3
_
2
___
-2п
3
1
__
3п
2
-п
__
2
-п
__
3
-п
__
4
-1
Х1= arctg 3/7+2П; Х2= -П/4 + 2П=7П/4.
3

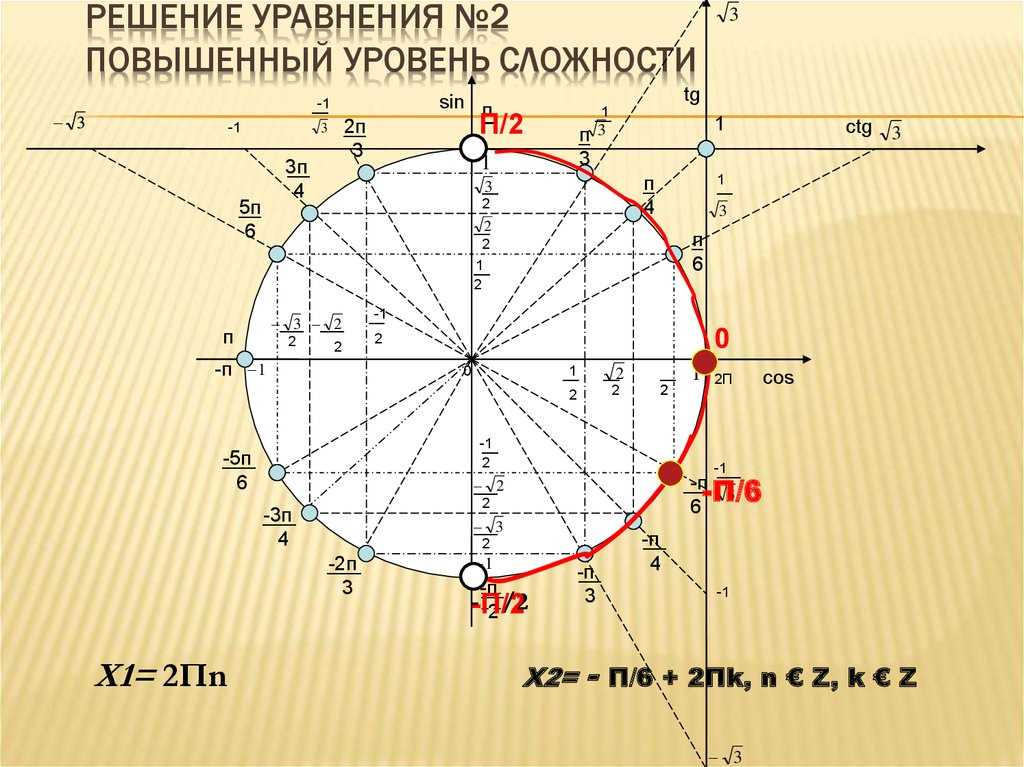
17. Решение уравнения №2 повышенный уровень сложности

РЕШЕНИЕ УРАВНЕНИЯ №2
ПОВЫШЕННЫЙ УРОВЕНЬ СЛОЖНОСТИ
3
-1
3п
__
4
5п
__
6
1
__
П/2
2п
__
3
3
tg
sin п
_
-1
__
1
п3
_
3
1
п
_
4
3
__
2
3
п
_
6
1
__
2
п
2
2
-п 1
ctg 3
1
__
__2
2
2
___
3 ___
3
-1
__
0
2
0
1
__
__2
2
2
__
2
1
2П
cos
3
-1
__
2
___
-5п
6
___
-3п
4
__3
_
2
___
-2п
3
Х1= 2Пn
-1
___
-п
__
3
-П/6
6
__2
_
2
1
-п
__
-П/2
-П/2
2
Х2=
-п
__
3
-
-п
__
4
-1
П/6 + 2Пk, n € Z, k € Z
3

18. Домашнее задание:

ДОМАШНЕЕ ЗАДАНИЕ:
ПРОБНЫЙ ЕГЭ. (обмен вариантами);
повторить п. 9, 11.