Similar presentations:
Методы решения тригонометрических уравнений
1. МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
2. I. СВЕДЕНИЕ К АЛГЕБРАИЧЕСКОМУ.
3.
Пример:3 cos 2 x 3sin x 0
3 (1 sin 2 x) 3sin x 0
3 1 sin 2 x 3sin x 0
Пусть sin x a,| a | 1 .
Уравнение примет вид:
a 2 3a 2 0
D 9 8 1
a1
3 1
2 - не удовлетворяет условию | a | 1
2
a2
3 1
1
2
sin x 1
x
Ответ: 2 n, n .
2
2
2 n, n
4. II. ОДНОРОДНЫЕ И СВОДИМЫЕ К НИМ.
5.
Уравнение видаa sin x b cos x 0
называется однородным
уравнением I степени.
6.
Пример:sin x cos x 0
Множество значений x, удовлетворяющих уравнению
cos x 0 , не является решением данного уравнения.
Поэтому можно обе части уравнения разделить на cos x 0
.
Получим:
tgx 1 0
tgx 1
x
Ответ:
4
n, n
.
4
n, n
7.
Уравнение видаa sin x b sin x cos x c cos x 0
2
2
называется однородным
уравнением II степени.
8.
Пример:2sin 2 x 3sin x cos x cos2 x 0
Решение:
Множество значений x, удовлетворяющих
уравнению cos x ,0не является решением
данного уравнения.
Разделим обе части уравнения на cos2 x 0 .
2
Получим: 2tg x 3tgx 1 0
9.
Пусть a tgx .Уравнение примет вид:
2a 3a 1 0
2
D 9 8 1
3 1
1
a1
4
2
1
tgx
2
1
x arctg n, n
2
3 1
a2
1
4
tgx 1
x
1
Ответ: arctg n, n ; k , k .
2
4
4
k, k
10. III. Если в уравнении содержится произведение функций sin(аx)sin(bx), sin(ax)cos(bx), cos(ax)cos(bx), то такие уравнения
III. ЕСЛИ В УРАВНЕНИИ СОДЕРЖИТСЯПРОИЗВЕДЕНИЕ ФУНКЦИЙ SIN(АX)SIN(BX),
SIN(AX)COS(BX), COS(AX)COS(BX), ТО ТАКИЕ
УРАВНЕНИЯ РЕШАЮТСЯ
ПРЕОБРАЗОВАНИЕМ ПРОИЗВЕДЕНИЯ В
СУММУ (РАЗНОСТЬ) И НАОБОРОТ.
11.
При этом применяют тождества:sin sin 2sin
cos
2
2
sin sin 2sin
cos
2
2
cos cos 2cos
cos
2
2
cos cos 2sin
sin
2
2
1
sin sin (cos( ) cos( ))
2
1
cos cos (cos( ) cos( ))
2
1
sin cos (sin( ) sin( ))
2
12.
Пример 1.cos3x cos x cos5 x cos7 x
1
1
cos 4 x cos 2 x cos 2 x cos12 x
2
2
cos 4 x cos12 x 0
2sin8 x sin 4 x 0
или
sin8 x 0
4x k, k
8 x n, n
x
n
Ответ: x
8
8
x
,n
n
,n
sin 4 x 0
.
k
4
,k
13.
Пример 2.sin x sin 3x sin 5 x sin 7 x 0
2sin 2 x cos x 2sin 6 x cos x 0
2cos x(sin 2 x sin 6 x) 0
2 2cos x sin 4 x cos x 0
2
cos x 0
x
Ответ:
2
2
n, n
sin 4 x 0
cos 2 x 0
4x k, k
2x
x
n, n ;
k
4
k
4
,k
,k ;
x
4
m
2
4
2
m, m
,m
m
2
.
,m
14. IV. Понижение степени.
IV. ПОНИЖЕНИЕСТЕПЕНИ.
15.
Если в уравнении содержатсячётные степени sinx и cosx, то
понижают степень уравнения с
применением понижающих
формул:
1 cos x
sin x
2
1 cos 2 x
2
cos x
2
2
2
16.
Пример.sin 2 x sin 2 5 x cos 2 2 x cos 2 4 x
1 cos 2 x 1 cos10 x 1 cos 4 x 1 cos8 x
2
2
2
2
cos 2 x cos 4 x cos8 x cos10 x 0
2cos3 x cos x 2cos9 x cos x 0
2cos(cos3 x cos9 x) 0
4cos x cos 6 x cos3x 0
cos x 0
x
2
n, n
6x
x
Ответ:
cos3 x 0
cos 6 x 0
2
n, n ;
2
12
12
k, k
k
6
k
6
,k
,k ;
3x
x
6
2
6
m
2
m, m
m
2
,m
,m .
17. V. Разложение на множители.
V. РАЗЛОЖЕНИЕ НАМНОЖИТЕЛИ.
18. Пример.
ПРИМЕР.4cos x sin x 2cos x 2sin x 1 0
2cos x(2sin x 1) (2sin x 1) 0
(2sin x 1)(2cos x 1) 0
1
sin
x
2
cos x 1
2
19. VI. ВВЕДЕНИЕ ВСПОМОГАТЕЛЬНОГО АРГУМЕНТА.
20.
Примерsin x cos x 1
Разделим обе части уравнения на
Получаем:
Решение:
a 2 b2 12 12 2
1
2
sin
sin x
4
1
2
cos x
sin x cos
4
1
2
cos x
1
2
1
cos( x )
4
2
x
x
4
4
x
Ответ:
4
2 n
4
,n
arccos
4
4
1
2
2 n, n
2 n, n
2 n
4
,n
21. VII. Применение универсальной подстановки.
VII. ПРИМЕНЕНИЕУНИВЕРСАЛЬНОЙ
ПОДСТАНОВКИ.
22. Универсальная подстановка:
УНИВЕРСАЛЬНАЯ ПОДСТАНОВКА:x
2tg
2
sin x
2 x
1 tg
2
x
1 tg
2
cos x
2 x
1 tg
2
2
23.
Пример2cos2 x 2tg 2 x 5
Решение:
1 tg 2 x
2
2tg 2 x 5
2
1 tg x
1 a
2
Пусть: tg x a, a 0. Уравнение примет вид 2
2a 5 0 . О.Д.З. a 1.
1 a
2(a 1) 2a (1 a ) 5(1 a ) 0
2 2 a 2 a 2 a 2 5 5a 0
2 a 2 5a 3 0
D 25 24 49
a1
5 7
3
4
Ответ:
a2
5 7
1
4
2
;
не удовлетворяет условию a 0
.
24.
Пример 2:sin x 3 cos x 3 0
Решение:
x
x
1 tg 2
2 3
2 3 0
x
x
1 tg 2
1 tg 2
2
2
x
x
x
2tg 3 3tg 2 3 3tg 2 0
2
2
2
x
tg 3
2
x
n, n
2
3
2
x
2 n, n
3
2tg
2
Ответ:
2 n, n
3
;
2 k , k.
Проверка:
x 2 k
0 3 3 0 - верно
25. VIII. Введение нового переменного.
VIII. ВВЕДЕНИЕНОВОГО ПЕРЕМЕННОГО.
26.
! Если в уравнении содержитсясумма или разность sinx и cosx и
их произведения, то уравнение
решается введением нового
переменного:
sin x cos x t
2
t 1
sin x cos x
2
sin x cos x t
1 t2
sin x cos x
2
27.
Пример:sin 2 x cos x sin x 1 0
2sin x cos x cos x sin x 1 0
Пусть:
sin x cos x t
t2 1
sin x cos x
2
t2 1 t 1 0
t2 t 2 0
t1 1
t 2 2
sin x cos x 1 или sin x cos x 2
(Решите самостоятельно)
28. IX. Использование понятия ограниченности (минимакс).
IX. ИСПОЛЬЗОВАНИЕПОНЯТИЯ ОГРАНИЧЕННОСТИ
(МИНИМАКС).
29.
Пример:5x
cos3 x cos 2
2
cos3 x 1
5
cos
1
2
x
x
2 k
2 k
4 n
3
4 n
3
5
5
k 2n
3 5
k
x
Ответ:
x 4 t , t .
3x 2 k
5
2 x 2 n
6n
5
n 5t
4
5t 4 t , t
5
k –целое


























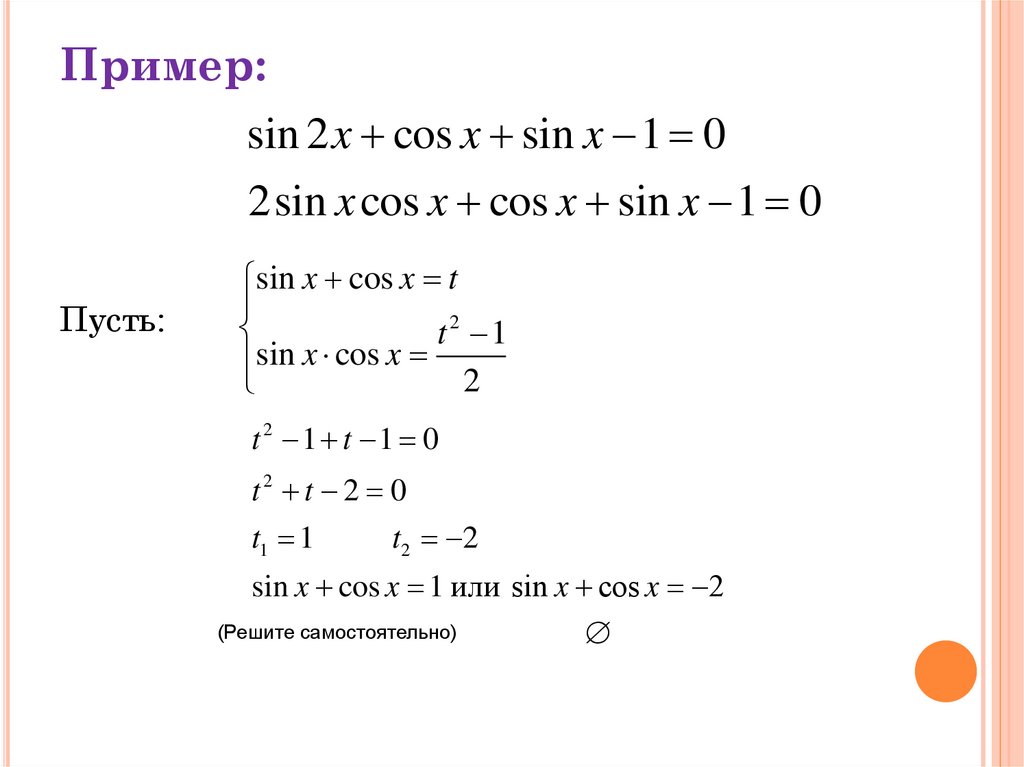


 mathematics
mathematics








