Similar presentations:
Тригонометрические уравнения и неравенства
1.
2.
Тригонометрия – раздел математики,изучающий соотношения между сторонами
и углами треугольника.
3.
4.
1. Решение тригонометрических уравнений, сводящихся куравнениям высших степеней.
3 sin x 2 cos 2 x 0
3 sin x 2(1 sin 2 x ) 0
3 sin x 2 2 sin 2 x 0
2 sin 2 x 3 sin x 2 0
Введём новую переменную t=sinx, -1 t 1. Получим:
2t 2 3t 2 0
D 9 4 2 ( 2) 9 16 25
t1, 2
t1
3 5
4
1
2
или
t 2 2 - не имеет смысла, т.к. -1 sinx 1 при x .
Вернёмся к исходной переменной x. Получим:
sin x
1
2
x ( 1) n arcsin
x ( 1) n
6
1
n , n
2
n , n
Ответ: x ( 1) n 6
n , n .
5.
2. Решение тригонометрических уравнений преобразованиемсуммы или разности тригонометрических функций в их
произведение.
cos 3 x sin 2 x sin 4 x 0
cos 3 x (sin 2 x sin 4 x ) 0
2x 4x
2x 4x
cos
0
2
2
cos 3 x 2 sin( x ) cos 3x 0
cos 3 x 2 sin
cos 3 x 2 sin x cos 3 x 0
cos 3 x (1 2 sin x ) 0
cos 3 x 0
3x
x
2
6
или
,
3
,
1 2 sin x 0
2 sin x 1
sin x
1
2
x ( 1) n arcsin
x ( 1) n
Ответ: x , , x ( 1) n
6
3
6
6
1
2 n, n
2
2 n, n Z
2 n , n Z
6.
3. Решение тригонометрических уравнений преобразованиемпроизведения тригонометрических функций в их сумму или
разность.
sin 5 x cos 3 x sin 6 x cos 2 x
1
1
(sin( 5 x 3 x ) sin( 5 x 3 x )) (sin( 6 x 2 x ) sin( 6 x 2 x ))
2
2
1
1
(sin 8 x sin 2 x ) (sin 8 x sin 4 x )
2
2
sin 8 x sin 2 x sin 8 x sin 4 x 0
sin 2 x sin 4 x 0
2x 4x
2x 4x
cos
0
2
2
sin( x ) cos 3 x 0
2 sin
sin x cos 3 x 0
sin x cos 3 x 0
sin x 0
x n, n
или
cos 3x 0
3x
x
2
6
,
3
,
Ответ: x n , n ,
x
6
3
,
7.
4. Решение тригонометрических уравнений разложением намножители.
sin 4 x 3 cos 2 x
sin 4 x 3 cos 2 x 0
2 sin 2 x cos 2 x 3 cos 2 x 0
cos 2 x ( 2 sin 2 x 3) 0
или
cos 2 x 0
2x
x
4
2
,
2
,
2 sin 2 x 3 0
sin 2 x 1,5 не имеет смысла,
потому что - 1 sin2x 1 при x ,
корней
Ответ: x
4
нет.
2
,
.
8.
5. Решение однородных уравнений.!
Уравнение является однородным, если в его правой части стоит 0.
Если вместо 0 находится любое число, то его следует представить
через основное тригонометрическое тождество.
В однородных уравнениях всегда можно делить на sinx либо
на cosx, т.к. они не могут одновременно равняться 0,
согласно основному тригонометрическому тождеству.
б) уравнение второй
а) уравнение первой
степени:
степени:
2
a sin x b cos x 0
a sin x b sin x cos x c cos 2 x 0
sin x cos x 0
sin 2 x 2 cos 2 x 3 sin x cos x
tgx 1 0
sin 2 x 3 sin x cos x 2 cos 2 x 0
tgx 1
tg 2 x 3tgx 2 0
x arctg1 k , k
x
4
Ответ:
tgx 2
x
4
x arctg1 k , k
x arctg 2 k , k
k , k
tgx 1
или
x
k , k
.
Ответ:
arctg 2 k , k
;
4
4
k , k
k , k .
9.
6. Решение уравнений методом понижения степени.sin 2 x sin 2 2 x sin 2 3x sin 2 4 x 2
1 cos 2 x 1 cos 4 x 1 cos 6 x 1 cos 8 x
2
2
2
2
2
1 cos 2 x 1 cos 4 x 1 cos 6 x 1 cos 8 x 4
4 (cos 2 x cos 4 x ) (cos 6 x cos 8 x ) 4
2x 4x
2x 4x
6x 8x
6x 8x
cos
2 cos
cos
4
2
2
2
2
4 2 cos 3x cos x 2 cos 7 x cos x 4
2 cos 3x cos x cos 7 x cos x 2
4 2 cos
cos 3x cos x cos 7 x cos x 0
cos x (cos 3x cos 7 x ) 0
3x 7 x
3x 7 x
cos
0
2
2
2 cos x cos 5 x cos 2 x 0
или
cos 5 x 0
или
cos x 0
5
x
n, n
x ,
2
2
n
x
,n
10
5
Ответ: , ; n , n
10
5
2
cos x 2 cos
cos 2 x 0
2x
x
;
2
m , m
m
,m
4
2
m
,m .
4
2
10.
7. Решение тригонометрических уравнений, содержащихтригонометрическую функцию под знаком радикала.
1 cos x sin x
1 cos x sin 2 x
sin x 0
1 cos x sin 2 x 0
sin x 0
sin 2 x cos x 1 0]
sin x 0
1 cos 2 x cos x 1 0
sin x 0
cos x cos 2 x 0
sin x 0
cos x (1 cos x ) 0
sin x 0
11.
cos x 01 cos x 0
sin x 0
sin x 0
cos x 1
x
k , k Z
sin x 0
2
sin x 0
y
x 2 т, т Z
sin x 0
2
P(1;0)
0
x
x
2
0
P(1;0)
2
2 k , k Z
Ответ:
x 2 т , т Z
2
2 k , k Z ; 2 т , т Z
.
12.
8. Решение тригонометрических уравнений вида:sin x sin y
x y 2 k , k или
cos x cos y
x y 2 k , k или
x y 2 n , n
x y 2 n , n
tgx tgy x y k , k
а) sin 2 x sin 4 x
2 x 4 x 2 k , k
или
6 x 2 k , k
x
6
Ответ:
6
k
3
,k
k
3
, k ; k , k .
2 x 4 x 2 k , k
2 x 2 k , k
x k , k
13.
б) cos x cos 5 xx 5 x 2 k , k
или
4 x 2 n, n
6 x 2 k , k
x
k
3
x
,k
Ответ:
x
в) tg tg7 x
3
x
7 x k , k
3
x 21x
k , k
3
20 x 3 k , k
x
3 k
,k
20
x 5 x 2 n, n
k
3
, k ;
Ответ: 3 k , k .
20
n
2
n
2
,n
,n .
14.
9. Решение линейных уравнений вида:a sin x b cos x c
1 сп. 3 sin x cos x 2
( 3 ) 2 12
3
1
sin x cos x 1
2
2
cos
sin
6
6
sin x cos cos x sin 1
6
6
sin( x
x
6
) 1
k , k
6
2
3
x
k , k
6
6
x
3
k , k
Ответ:
3
k, k .
15.
2 сп.3 sin x cos x 2
x
2 2
3
x
x
1 tg 2
1 tg 2
2
2
x
x
2 3tg 1 tg 2
2
2 2
x
1 tg 2
2
2tg
x
2
1 tg 2
Введем новую переменную t tg
2 3t 1 t 2
2
2
1 t
2 3t 1 t 2 2 2t 2
1 t2 0
3t 2 2 3t 1 0
t 2 1
- верно при t R
x
, получим :
2
16.
3t 2 2 3t 1 0D 12 4 3 1 0, D 0
2 3
6
3
t
3
Вернемся к исходной переменной x, получим :
t
tg
x
3
2
3
x
3
arctg
,
2
3
x
,
2 3
2
x
,
3
Проверка:
3 sin( 2 ) cos( 2 ) 2
0 1 2- неверно, значит, 2 , , не являются корнями уравнения.
Ответ: 2 , .
3
17.
3 сп.3 sin x cos x 2
x
x
x
x
3 sin( 2 ) cos( 2 ) 2 sin 2 2 cos 2
2
2
2
2
x
x
x
x
x
x
2 3 sin cos cos 2 sin 2 2 sin 2 2 cos 2 0
2
2
2
2
2
2
x
x
x
x
cos 2 2 3 sin cos 3 sin 2 0
2
2
2
2
x
x
(cos 3 sin ) 2 0
2
2
x
x
cos 3 sin 0
2
2
x
1 3tg 0
2
x
1
tg
2
3
x
1
arctg
,
2
3
x
3
2 ,
Ответ:
3
2 ,
.
18.
10. Решениеуравнений вида:
P (sin x cos x ; sin x cos x ) 0
sin x cos x 1 2 sin 2 x
sin x cos x 4 sin x cos x 1 0
Введем новую переменную t sinx cosx
t 2 (sin x cos x ) 2
t 2 sin 2 x 2 sin x cos x cos 2 x
2 sin x cos x t 2 1
4 sin x cos x 2t 2 2
t 1 2t 2 2 0
2t 2 t 3 0
D 1 4 2 ( 3) 25, D 0
1 5
4
t 1
t
или
t 1,5
Вернемся к исходной переменной х. Получим:
, получим :
19.
sin x cos x 1,5sin x cos x 1
1
1
3
sin x
cos x
2
2
2 2
1
1
1
sin x
cos x
2
2
2
cos
4
sin x cos
sin( x
4
4
sin
cos
4
sin
1
2
x
4
n
( 1)
x ( 1) n
n
4
4
4
4
sin( x
2
x ( 1) arcsin
n , n
4
2
sin
n, n
4
4
4
4
)
смысла, т.к.
при
n , n
n
Ответ: ( 1)
1
sin x cos sin cos x
4
4
2
1
2
)
4
cos x
n , n .
3 2
4
- не имеет
1 sin( x
4
) 1,
x , значит, корней нет.
20.
11. Решение тригонометрических уравнений сиспользованием свойств ограниченности функции.
sin x sin 9 x 2
1 sin x 1
1 sin 9 x 1
2 sin x sin 9 x 2
Значит, равенство sinx sin9x 2 возможно,
если
y
sinx 1
2
sin9x 1
x
2
9x
x
x
Ответ:
2 ,
2
2
n, n
2 ,
2 n
,n
18 9
x
2
2 , .
x
2
5
18
P(1;0)
0 18 x
6
n 0 x
18
2 5
n 1 x
18
9
18
2
n 1 x
18
9
6
4
n 2 x
18
9
2
2 ,
21.
ЗАПОМНИТЬ!!!Если система содержит 2
тригонометрических уравнения, то
нельзя решать с помощью проверок,
т.к. может произойти потеря корней.
Нужно решить оба уравнения и по
тригонометрическому кругу найти
общее решение.
22.
12. Решение уравнений, содержащих обратныетригонометрические функции.
2
а) arctg ( x 3 x 3)
tg
x 2 3x 3
4
1 x 2 3x 3
x 2 3x 4 0
x 4 или x -1
Ответ: 4; -1 .
4
23.
5x 15 x 1 5
2 arccos
б) arcsin
3
3
6
arccos a
2
arcsin a при a 1.
5x 1
5x 1
5
2( arcsin
)
3
2
3
6
5x 1
5 x 1 5
arcsin
2 arcsin
3
3
6
5 x 1 5
arcsin
\6
3
6
5x 1
arcsin
3
6
5x 1
sin
3
6
5x 1
1
1
3
arcsin
24.
5x 1 13
2
3 5x 1 3
10 x 2 3
2 5x 4
10 x 5
0,4 x 0,8
x 0,5
0,4 x 0,8
x 0,5
Ответ: 0,5 .
25.
13. Особые приёмы решения тригонометрическихуравнений.
а) (1 sin x )( tg 2 x 3) 0
или
1 sin x 0
x
,
2
sinx 1
x
x
x
2
2
,
2 n, n
,
2
решений нет
Ответ:
3
, .
tg 2 x 3 0
x
l , l
2
tg 2 x 3
x
l , l
2
tgx 3
или tgx 3
l , l
x
,
x
l , l
x
,
x
x
x
x
x
2
3
2
3
2
2
l , l
3
,
l , l
3
,
26.
б) sin 2 x sin x 2 cos x 12 sin x cos x sin x 2 cos x 1 0
( 2 sin x cos x sin x ) ( 2 cos x 1) 0
sin x ( 2 cos x 1) ( 2 cos x 1) 0
( 2 cos x 1)(sin x 1) 0
2 cos x 1 0
или
sin x 1
1
cos x
2
1
x arccos 2 ,
2
x
3
2 , или x -
x
3
2 n, n
Ответ: 2 n, n , 2 m, m .
3
sin x 1 0
2
2
2 m, m
27.
14. Решение тригонометрических уравнений смешанноготипа.
а) 1 - cos(lgx) 2 sin(lg
1 cos(lg x ) 2 sin(
x)
1
lg x ) 0
2
1
Введем новую переменную t lg x, получим :
2
1 - cos(2t) - 2 sin t 0
cos 2 t sin 2 t cos 2 t sin 2 t 2 sin t 0
2 sin 2 t 2 sin t 0
sin t ( 2 sin t 2 ) 0
sin t 0
или
t k , k
2sint - 2 0
sint
2
2
t (-1) n
4
n, n
28.
Вернемся к исходной переменной x, получим:1
lg x k , k
2
lg x 2 k , k z
x 10
2
1
lg x ( 1) n n, n
2
4
или
lg x ( 1) n
,k
2
2 n , n
x 10
( 1) n 2 n
2
,n
Область определения исходного уравнения x>0, т.е. оба корня
являются решением данного уравнения.
Ответ: 10
2
, k , 10
( 1) n 2 n
2
,n .
29.
б) sin( x 3 2 x 2 1) x 2 2 x 31. Оценим левую часть уравнения :
- 1 sin(x 3 2 x 2 1) 1, при x
2. Оценим правую часть уравнения :
x 2 2 x 3 ( x 2 2 x 1) 2 ( x 1) 2 2
( x 1) 2 0 при x
(x 1) 2 2 2
Т.к. - 1 sin(x 3 2 x 2 1) 1 и x 2 2 x 3 2 ,то в уравнении корней
нет.
Ответ: корней нет.
30.
31.
Алгоритм решения неравенств вида:cos x a
sin x a
(для знаков , , )
1.Отметить точку А на оси Ох (Оу) и провести через неё
прямую, перпендикулярную этой оси.
2.Отложить на окружности дугу, состоящую из всех
точек окружности, абсциссы (ординаты) которых
удовлетворяют этому неравенству.
* Эти все точки расположены по одну сторону от
проведённой прямой.
3.Записать промежуток, прибавив к его концам 2 .
* Левое число всегда меньше правого.
32.
Примеры.1)
y
2
cosx
2
4
4
2 x
Ответ:
4
2 ,
0
2
;
2
, .
4
4
2) sin( x ) 2
4
2
2 x 2 2 ,
Ответ: 2 ;2 2 , .
2
P(1;0)
2
2
4
x
y
2
3
9
2 x
2 ,
4
4
4
3
9
2 x
2 ,
4
4
4
4
3
4
2
2
0
9
4
P(1;0)
x
33.
23) tg3 x 3
2
6
3 x
3
x
3
2
,
9
3
,
0
Ответ:
6
3
;
3
y
9
,
3
.
2
3
1
P(1;0)
x










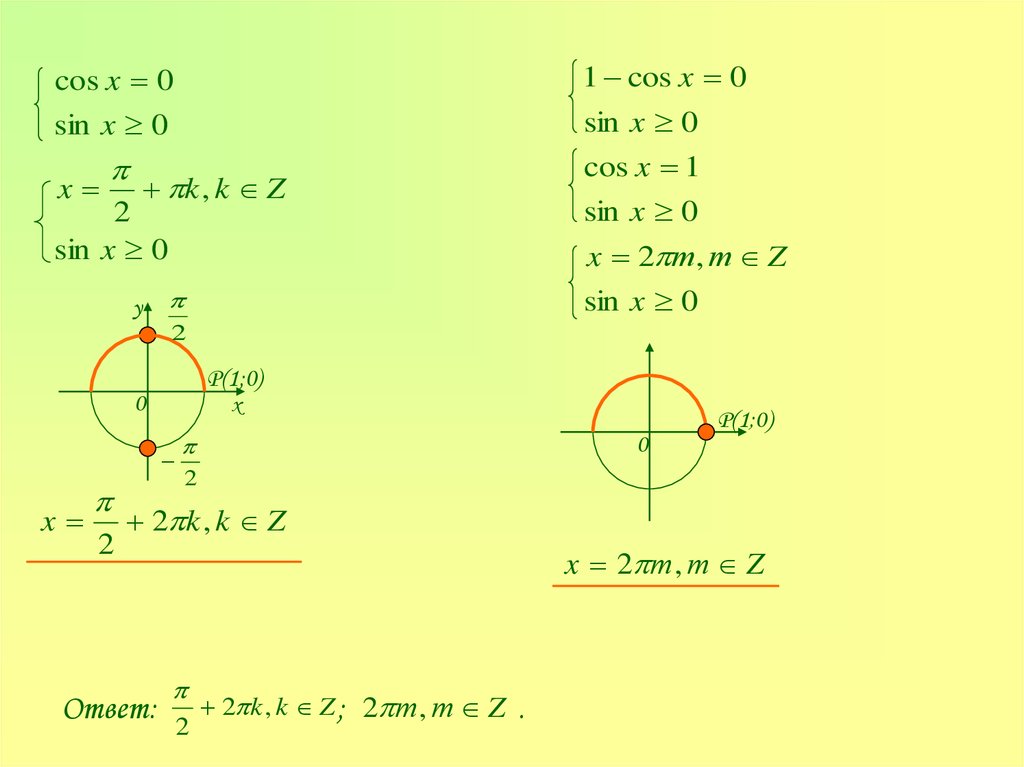

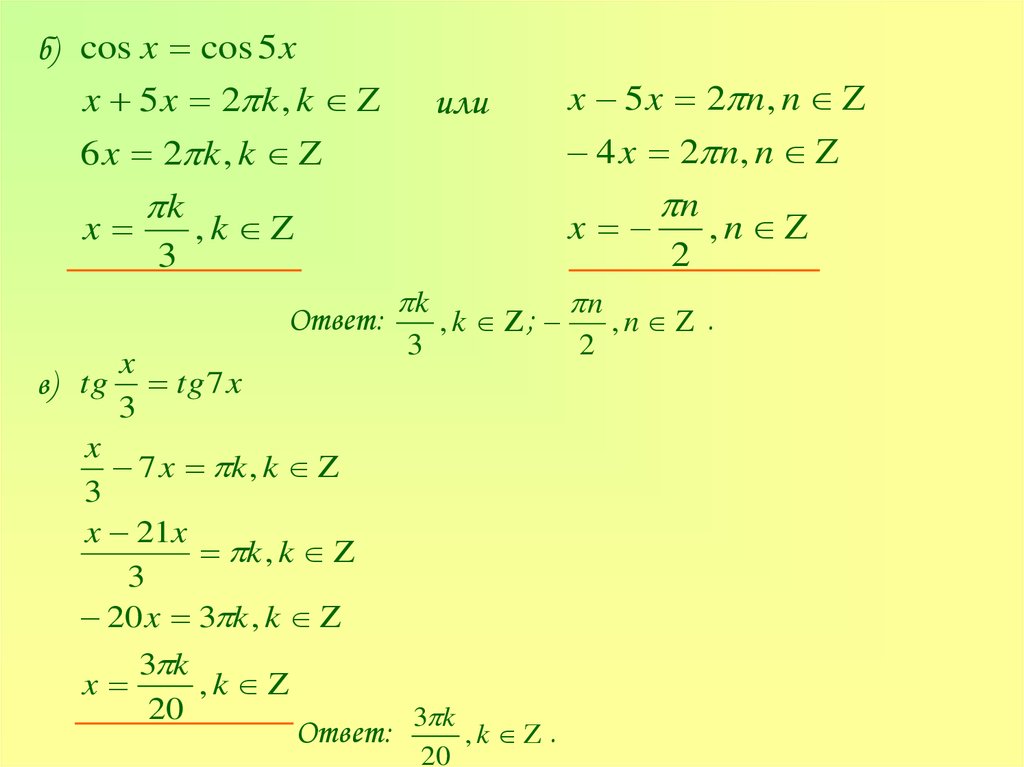

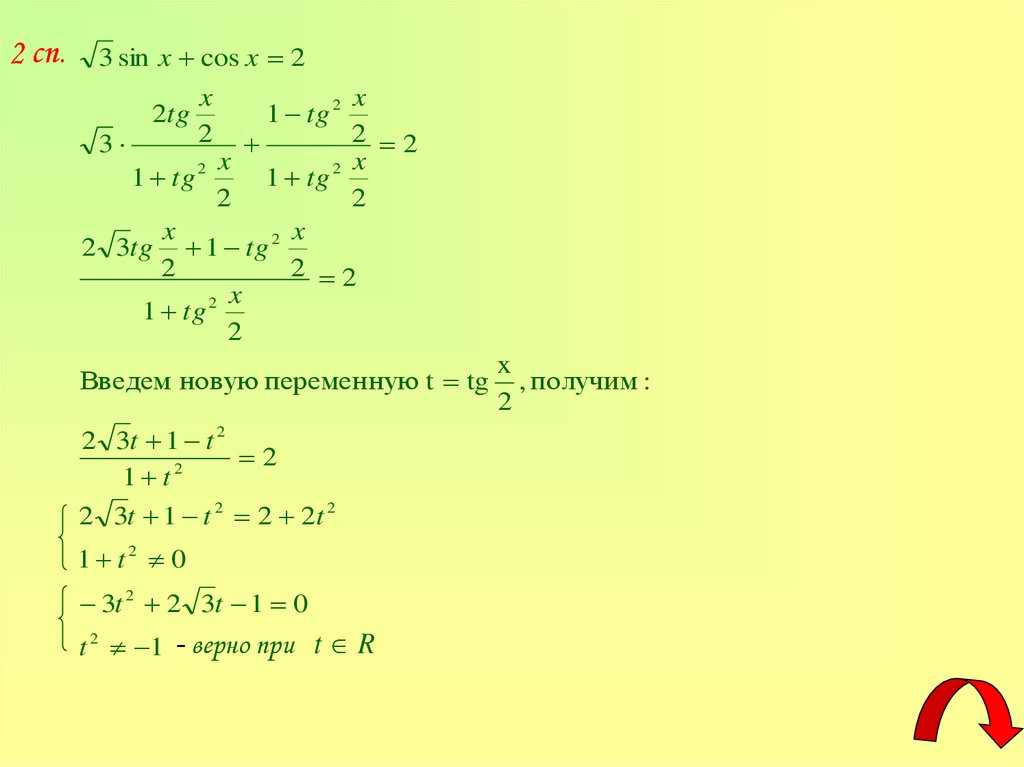

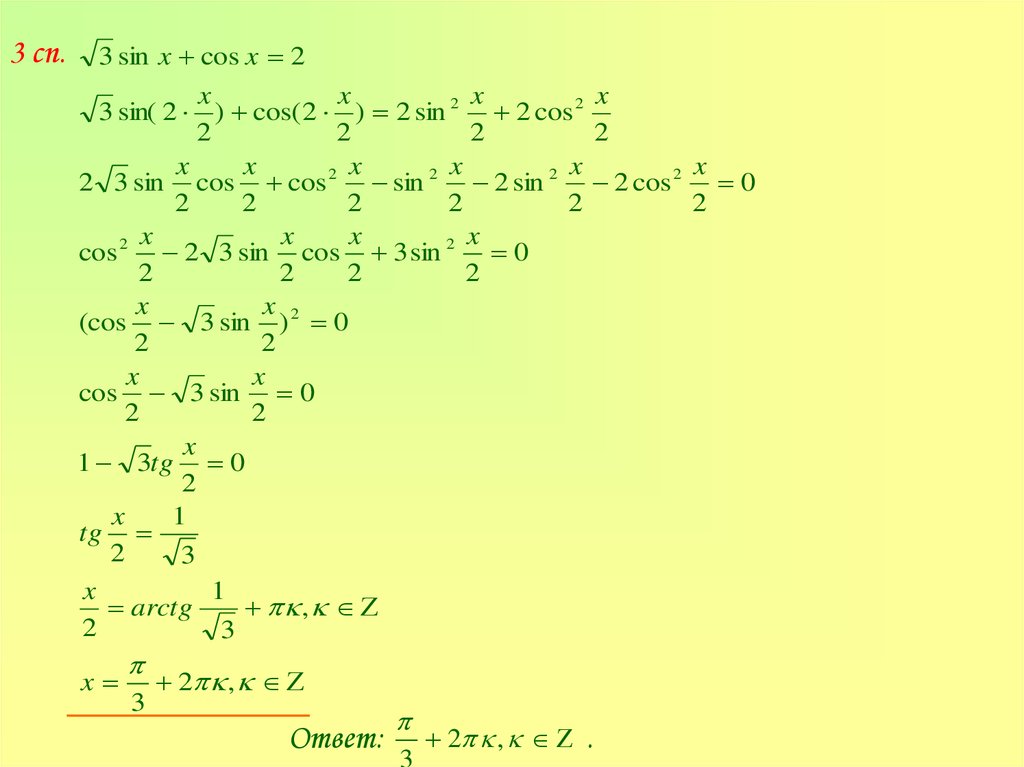

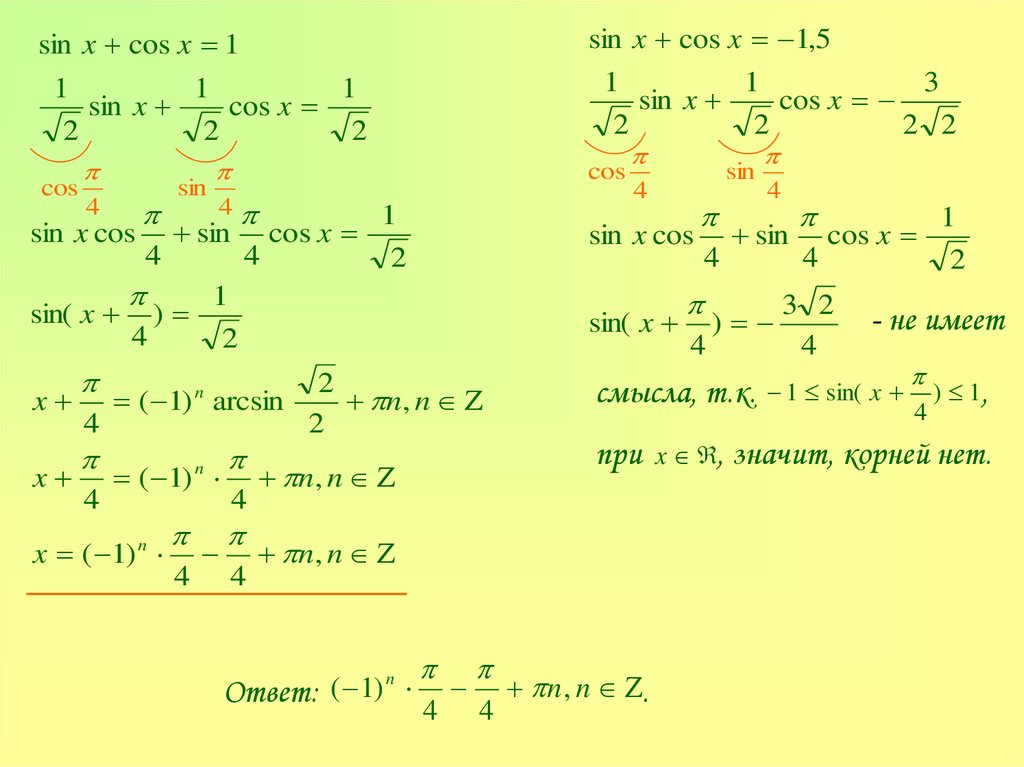






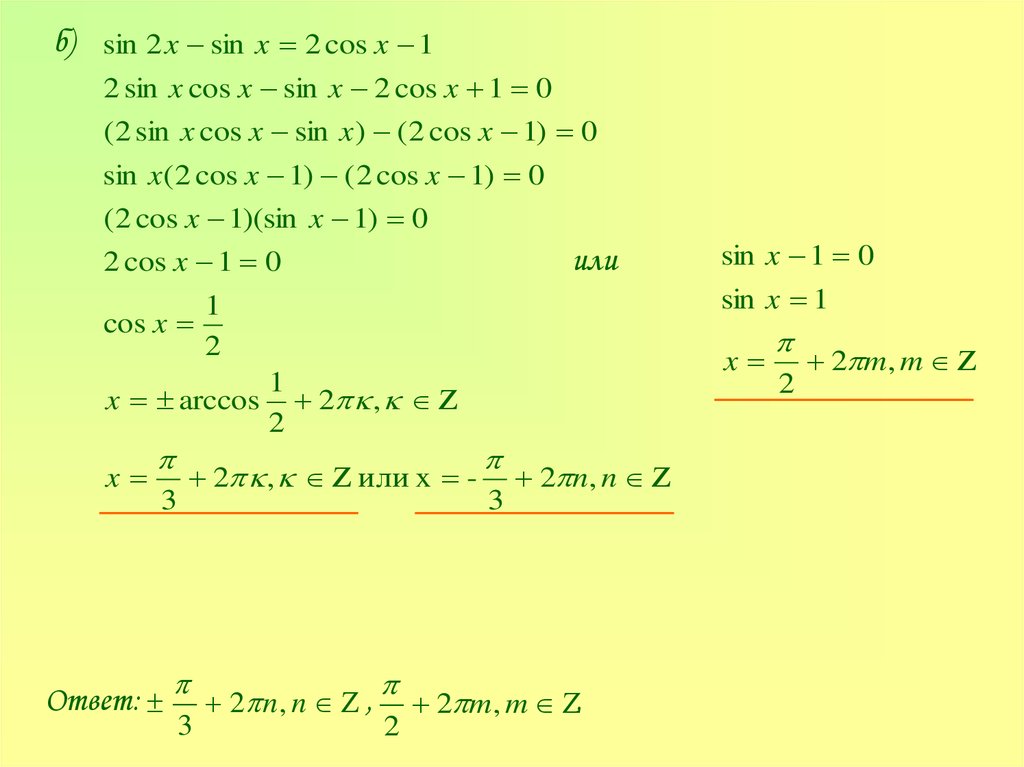





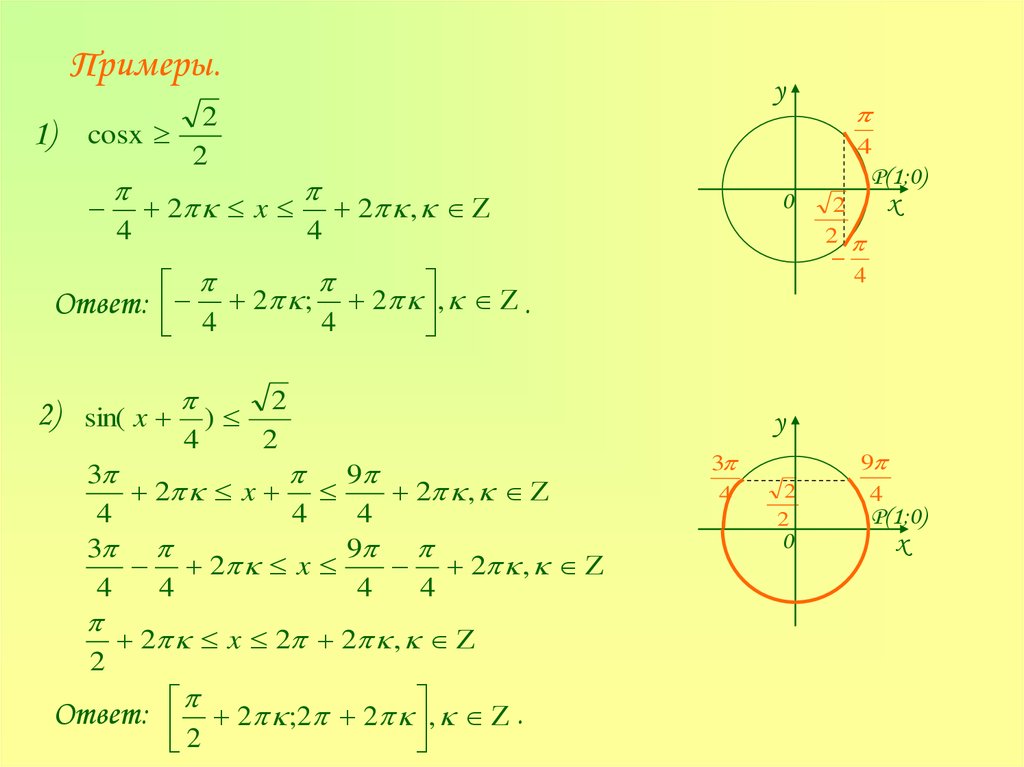
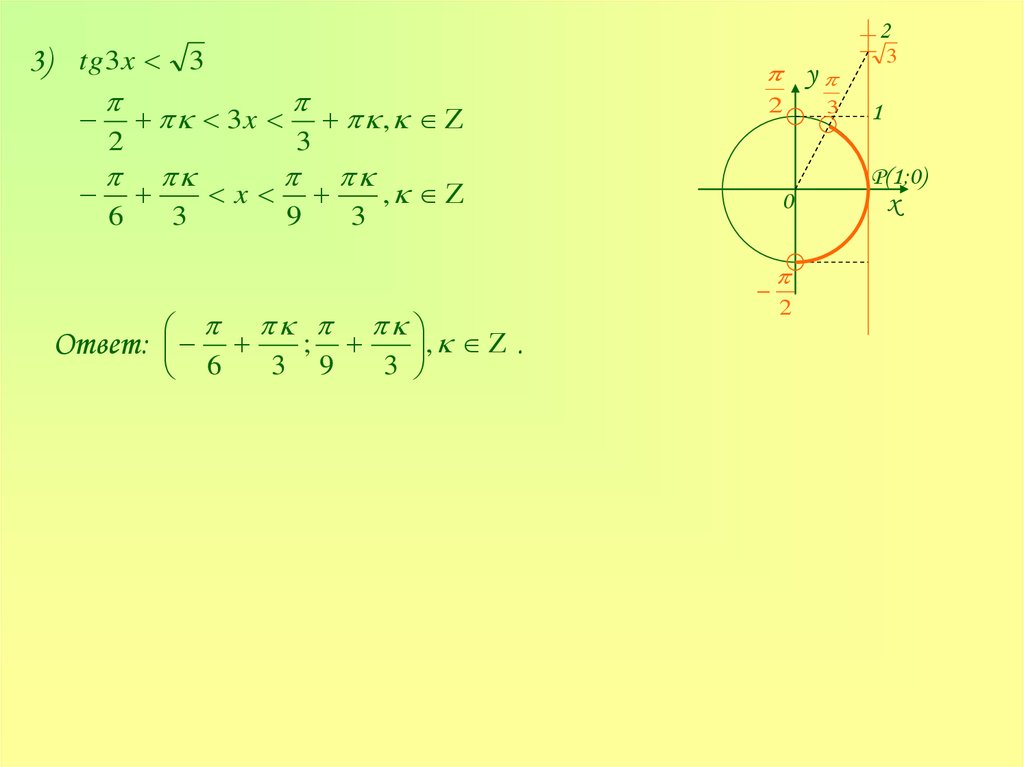
 mathematics
mathematics








