Similar presentations:
Решение простейших тригонометрических уравнений
1. «РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ»
2.
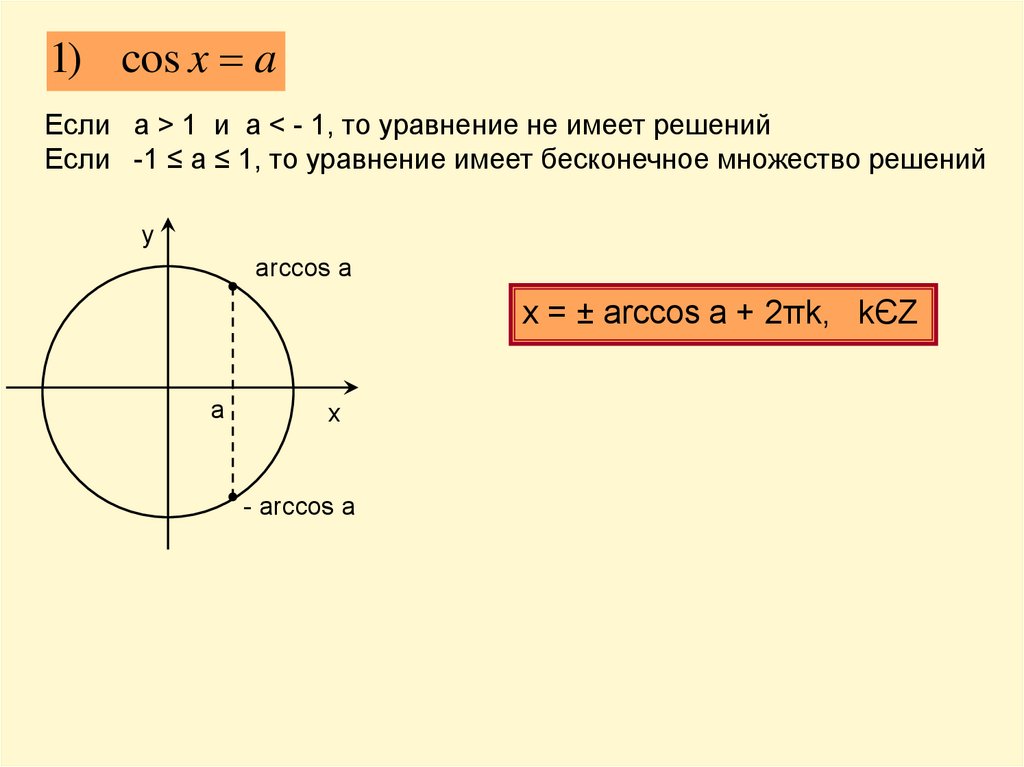
1) cos x aЕсли a > 1 и а < - 1, то уравнение не имеет решений
Если -1 ≤ a ≤ 1, то уравнение имеет бесконечное множество решений
у
arccos a
x = ± arccos a + 2πk, kЄZ
a
х
- arccos a
3.
Особая форма записи решения уравнений вида:cos x = 1
cos x = -1
cos x = 0
у
у
х
x 2 k, k Z
у
х
x π 2 k, k Z
х
π
x πk, k Z
2
4.
Пример 1. Решите уравнение1
x arccos 2 k , k Z ,
2
x 2 k , k Z .
3
2
2
2 k , k Z .
б ) cos x
, x arccos
2
2
1
a ) cos x ,
2
x 2 k , k Z ,
4
3
x
2 k , k Z .
4
2
2
в ) cos x , x arccos 2 k , k Z .
3
3
г ) cos x 3, нет решений, т.к. 3 1
5.
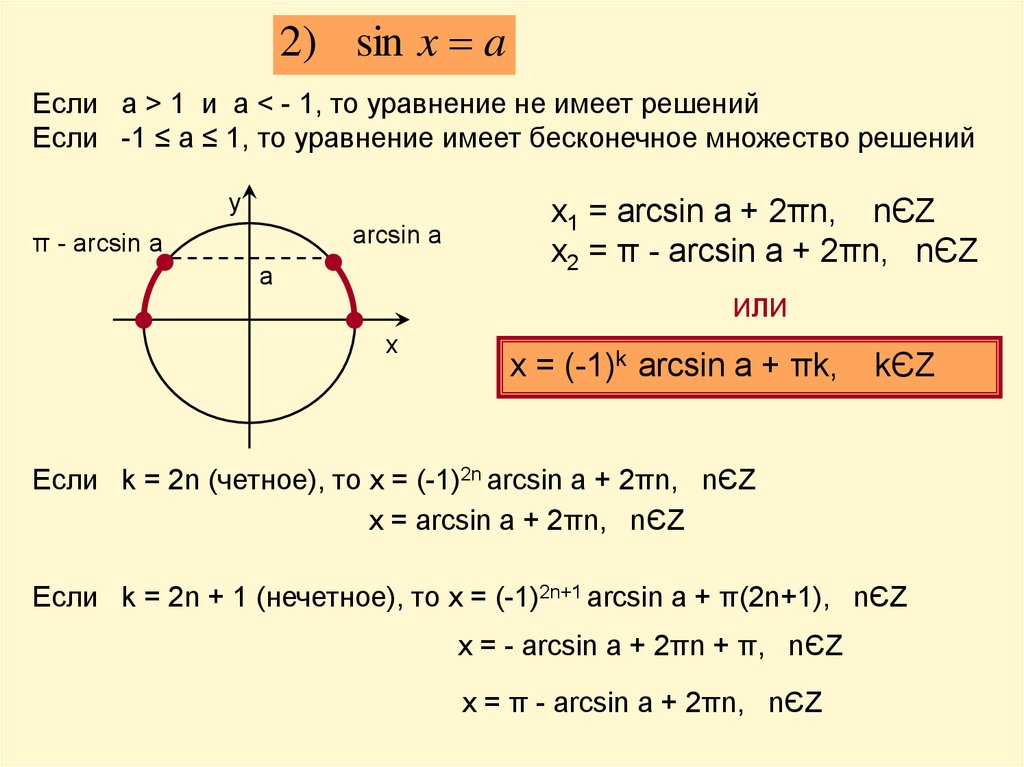
2) sin x aЕсли a > 1 и а < - 1, то уравнение не имеет решений
Если -1 ≤ a ≤ 1, то уравнение имеет бесконечное множество решений
у
arcsin a
π - arcsin a
a
x1 = arcsin a + 2πn, nЄZ
x2 = π - arcsin a + 2πn, nЄZ
ИЛИ
х
x = (-1)k arcsin a + πk,
kЄZ
Если k = 2n (четное), то x = (-1)2n arcsin a + 2πn, nЄZ
x = arcsin a + 2πn, nЄZ
Если k = 2n + 1 (нечетное), то x = (-1)2n+1 arcsin a + π(2n+1), nЄZ
x = - arcsin a + 2πn + π, nЄZ
x = π - arcsin a + 2πn, nЄZ
6.
Особая форма записи решения уравнений вида:sin x = 1
sin x = -1
у
у
x
2
2 k, k Z
у
х
х
sin x = 0
x
2
2 k, k Z
х
x πk, k Z
7.
Пример 2. Решите уравнение3
x 1 arcsin
k , k Z ,
2
k
x 1 k , k Z .
3
2
2
k
k , k Z .
б ) sin x
, x 1 arcsin
2
2
2
k 1
k
k , k Z ,
x 1 arcsin
k , k Z , x 1
4
2
3
a ) sin x
,
2
k
1
1
в ) sin x , x 1 k arcsin k , k Z .
7
7
г ) sin x 2, нет решений, т.к. 2 1
8.
3) tgx aНа ; уравнение tgx a имеет единственный
2 2
корень x arctga
Т.к. функция у = tg x периодическая с основным периодом π, то
значение функции будет повторяться через πk, kЄZ.
Следовательно,
x = arctg a + πk, kЄZ
- все решения
уравнения tg x = a
9.
Пример 3. Решите уравнениеa) tgx 3 ,
x arctg 3 k , k Z ,
x
б ) tgx 1,
x
4
3
k , k Z .
x arctg 1 k , k Z.
k , k Z .
в ) ctgx 3 ,
1
tgx
,
3
1
x arctg
k , k Z ,
3
x
6
k , k Z .







 mathematics
mathematics








