Параллельность прямых в пространстве

1.

D
A
C
B

2.

1.Изучить внимательно тему
2.Решить задачу слайд №10. Образец задачи
на слайде №11,12

3.

Каково может быть взаимное
расположение двух прямых на
плоскости?
(совпадают, пересекаются, параллельны)
1
2
Дайте определение параллельных
прямых на плоскости.
Параллельными называются прямые, лежащие в
одной плоскости и не пересекающие друг друга.
a b
(
)
a , b
a∩b
© Кузьмина Е.А., Колобовская МСОШ, 2010

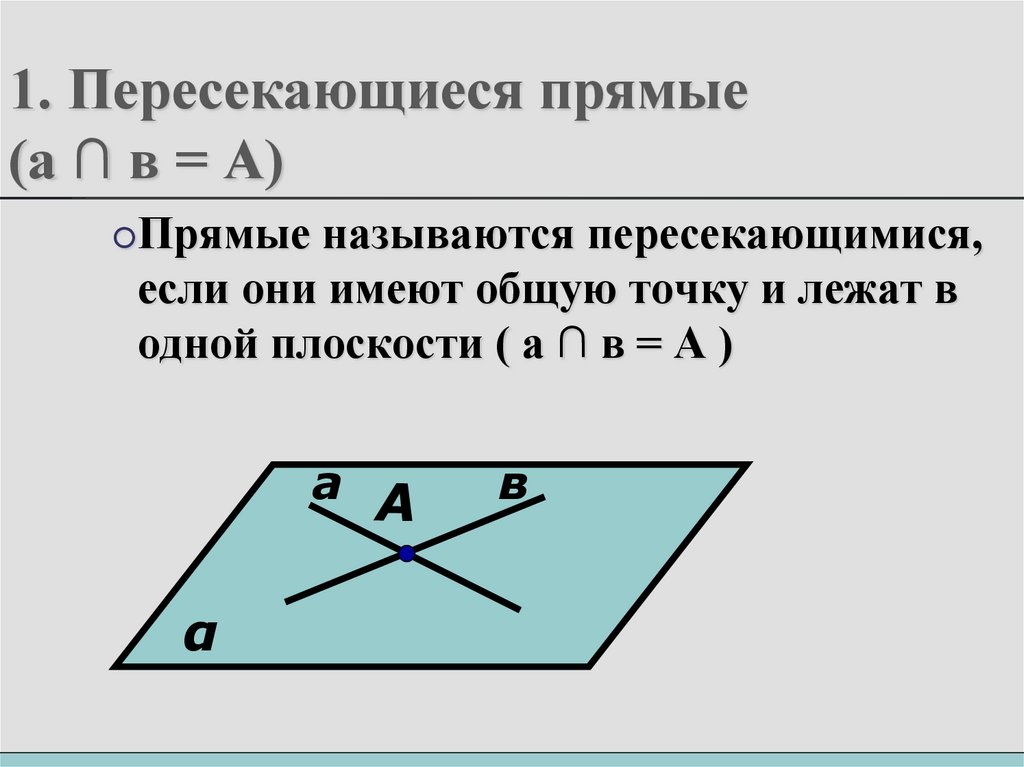
4. 1. Пересекающиеся прямые (а ∩ в = А)

Прямые
называются пересекающимися,
если они имеют общую точку и лежат в
одной плоскости ( а ∩ в = А )
а
α
в

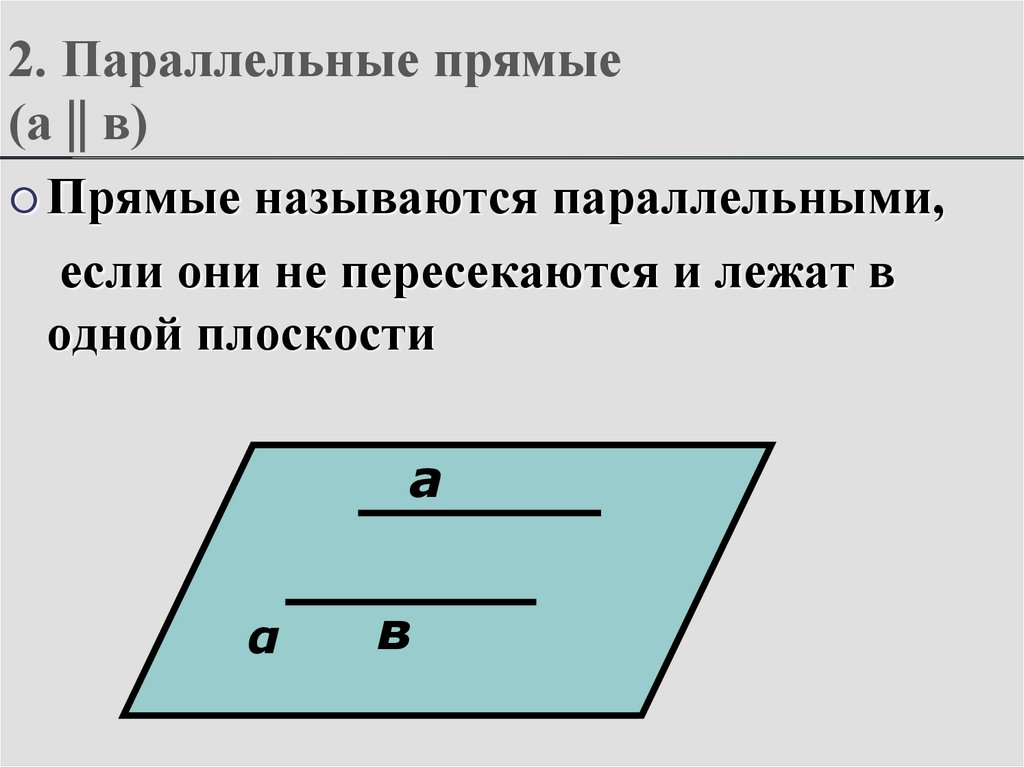
5. 2. Параллельные прямые (а || в)

Прямые называются параллельными,
если они не пересекаются и лежат в
одной плоскости
а
α
в

6.

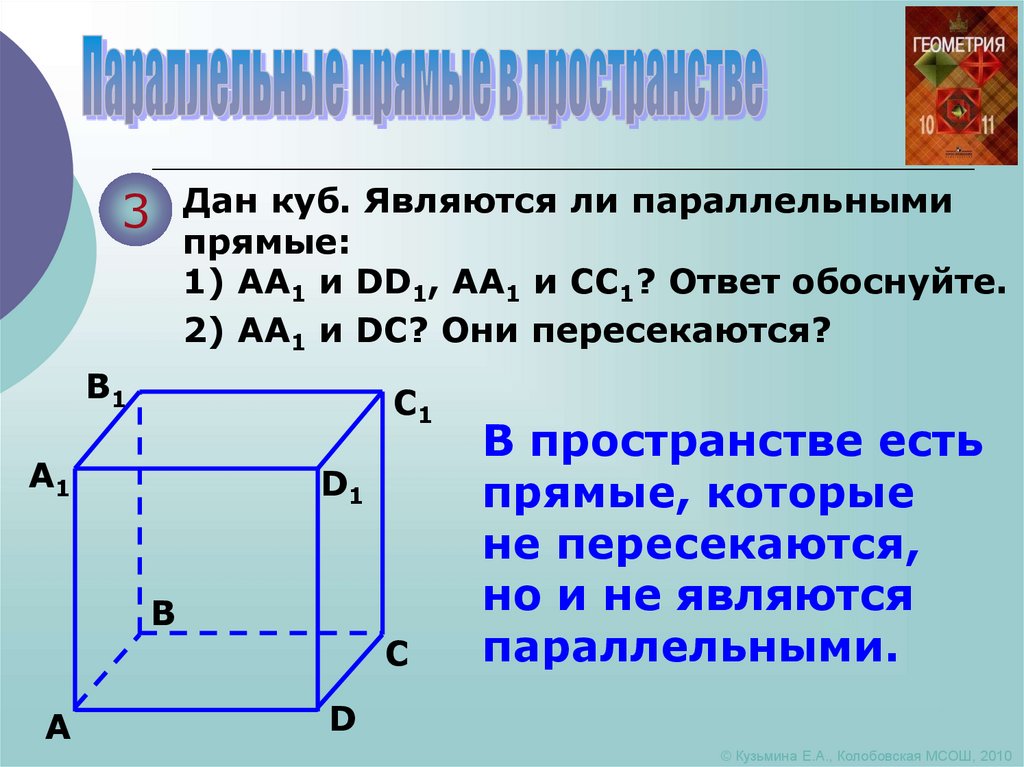
3
Дан куб. Являются ли параллельными
прямые:
1) АА1 и DD1, АА1 и СС1? Ответ обоснуйте.
2) АА1 и DС? Они пересекаются?
B1
C1
A1
D1
B
A
C
В пространстве есть
прямые, которые
не пересекаются,
но и не являются
параллельными.
D
© Кузьмина Е.А., Колобовская МСОШ, 2010

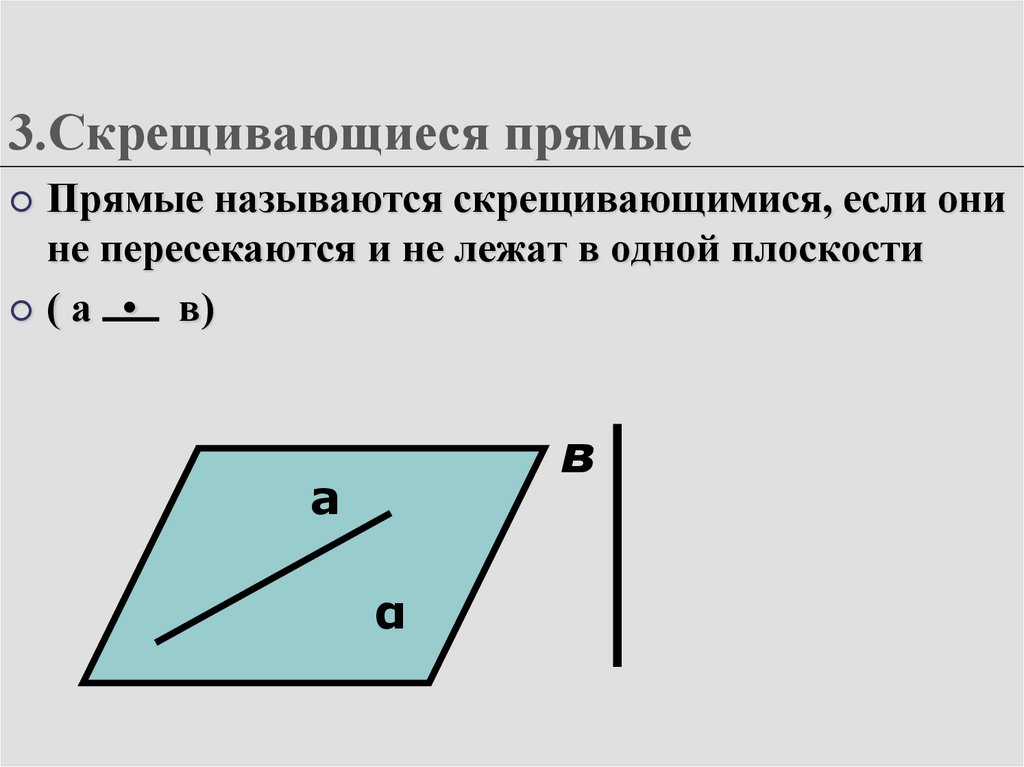
7. 3.Скрещивающиеся прямые

Прямые называются скрещивающимися, если они
не пересекаются и не лежат в одной плоскости
( а • в)
в
а
α
α

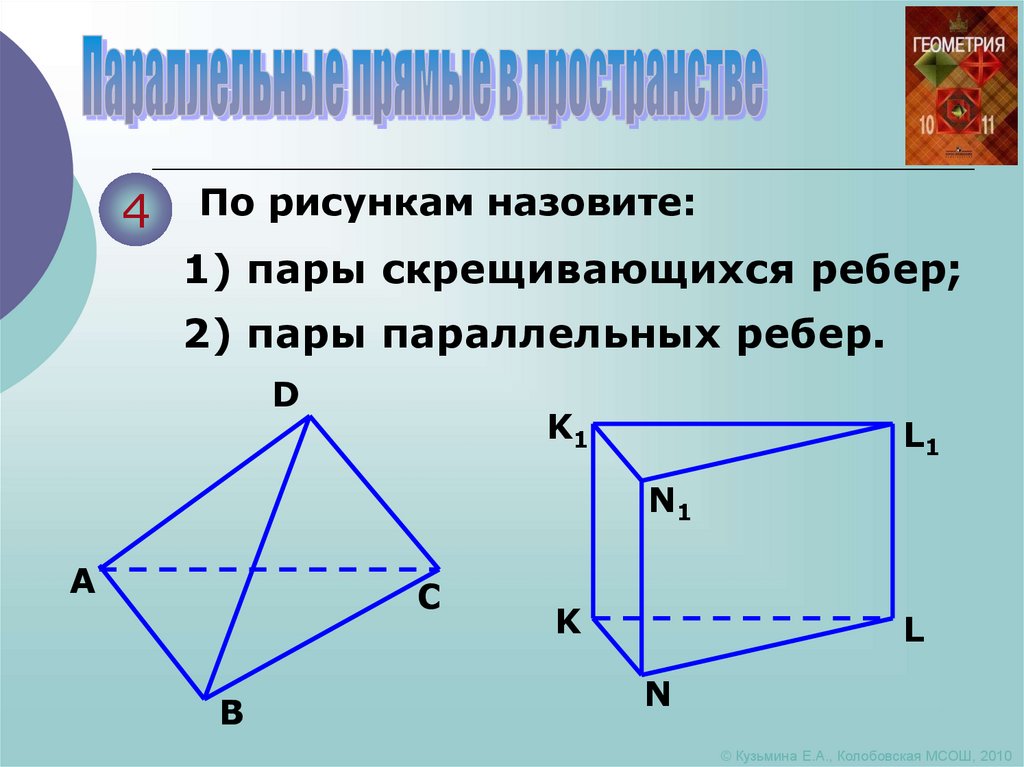
8.

4
По рисункам назовите:
1) пары скрещивающихся ребер;
2) пары параллельных ребер.
D
K1
L1
N1
A
C
B
K
L
N
© Кузьмина Е.А., Колобовская МСОШ, 2010

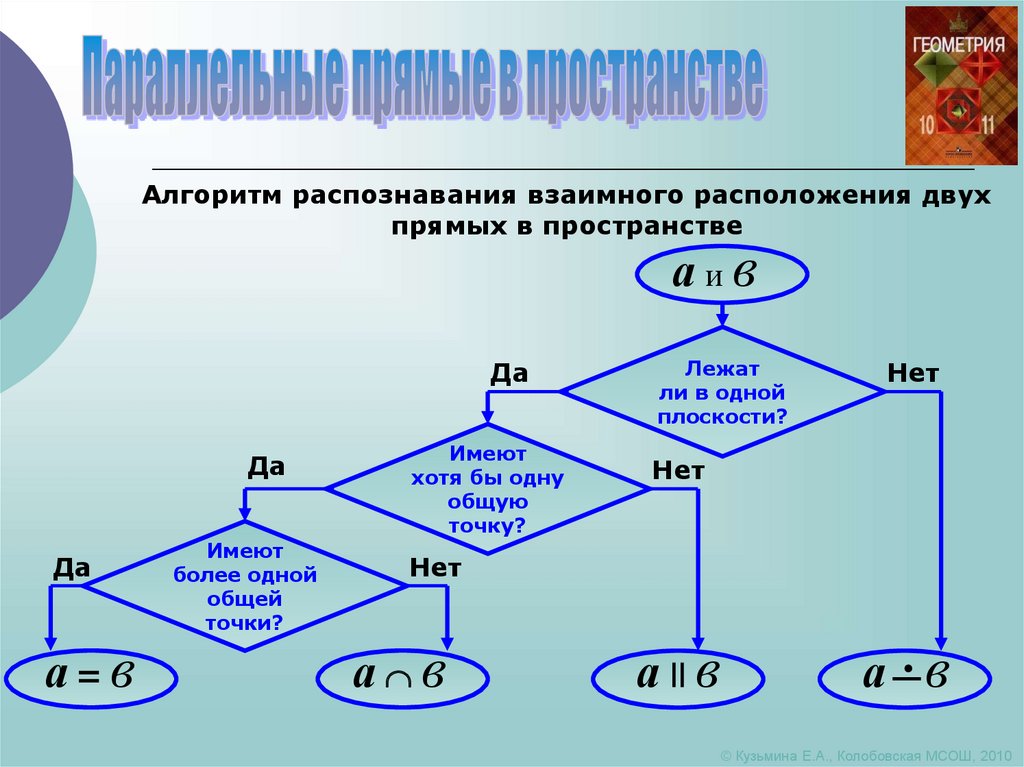
9.

Алгоритм распознавания взаимного расположения двух
прямых в пространстве
аив
Да
Да
Да
а=в
Имеют
более одной
общей
точки?
Имеют
хотя бы одну
общую
точку?
Лежат
ли в одной
плоскости?
Нет
Нет
Нет
а в
а
в
а .в
© Кузьмина Е.А., Колобовская МСОШ, 2010

10.

Решить задачу
Решить задачу
Через конец А отрезка АВ проведена плоскость.
Через
конец
А отрезка
проведена
Через конец
В и точку
С этого АВ
отрезка
проведены
параллельные
прямыеконец
, пересекающие
плоскость
плоскость. Через
В и точку
С
в точках В1 и С1.
этого
параллельные
Найдитеотрезка
длину ВВпроведены
,
если:
1
прямые
, пересекающие
плоскость в
1)СС1 = 15см,
АС:ВС= 2:3
В1 АВ:АС=11:9
и С1.
точках
2)СС1=8,1см
Найдите
длину1=2:5
ВВ1, если:
3)
АВ =6 смАС:СС
1)СС1 = 15см, АС:ВС= 2:3
2)СС1=8,1см АВ:АС=11:9
3)АВ =6 смАС:СС =2:5

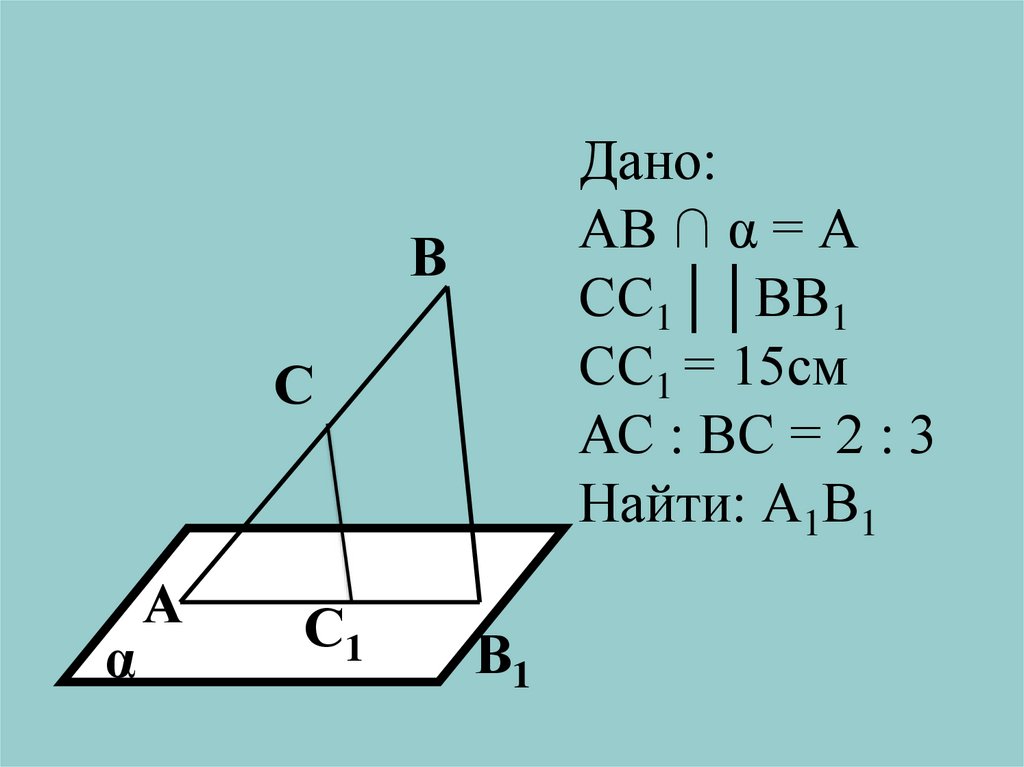
11.

Дано:
АВ ∩ α = А
СС1││ВВ1
СС1 = 15см
АС : ВС = 2 : 3
Найти: А1В1
В
С
α
А
С1
В1

12. Пример решения задачи

ΔАВВ1 подобен ΔА1СС1 , по двум углам:<С = <
В, при параллельных и секущей
<А – общий. В подобных треугольниках
стороны пропорциональны
ВВ1
АВ
АС
СС1
3 2
х
2
15
75 2 х
х 37,5
Ответ: А1В1= 37,5 см

13.

5
Всегда ли две непересекающиеся
прямые в пространстве параллельны?
6
Какие две прямые в пространстве
называются параллельными?
7
Дано: а
. Докажите, что все прямые,
пересекающие данные лежат в одной
плоскости.
8
в
Сколько можно провести в
пространстве прямых, проходящих
через данную точку, параллельных
данной прямой?
© Кузьмина Е.А., Колобовская МСОШ, 2010