Similar presentations:
Параллельные прямые в пространстве. Параллельность трех прямых. Параллельность прямых и плоскостей
1. Тема урока
Параллельные прямые впространстве .Параллельность
трех прямых. Параллельность
прямых и плоскостей.
2. Определение
• Две прямые в пространственазываются параллельными,
если они лежат в одной
плоскости и не
пересекаются.
3. Теорема 1.3
• Через любую точку пространства, нележащую на данной прямой, проходит
прямая, параллельная данной, и притом
только одна.
М
b
a
4. Определение
• Две прямые называютсяскрещивающимися, если
они не лежат в одной
плоскости.
5.
a и bНет
Да
Лежат ли в
одной
плоскости
Да
Имеют хотя
бы одну
общую
точку
Да
Нет
Имеют
более
одной
общей
точки
a ≡ b
Нет
a · b
a || b
a ∩b
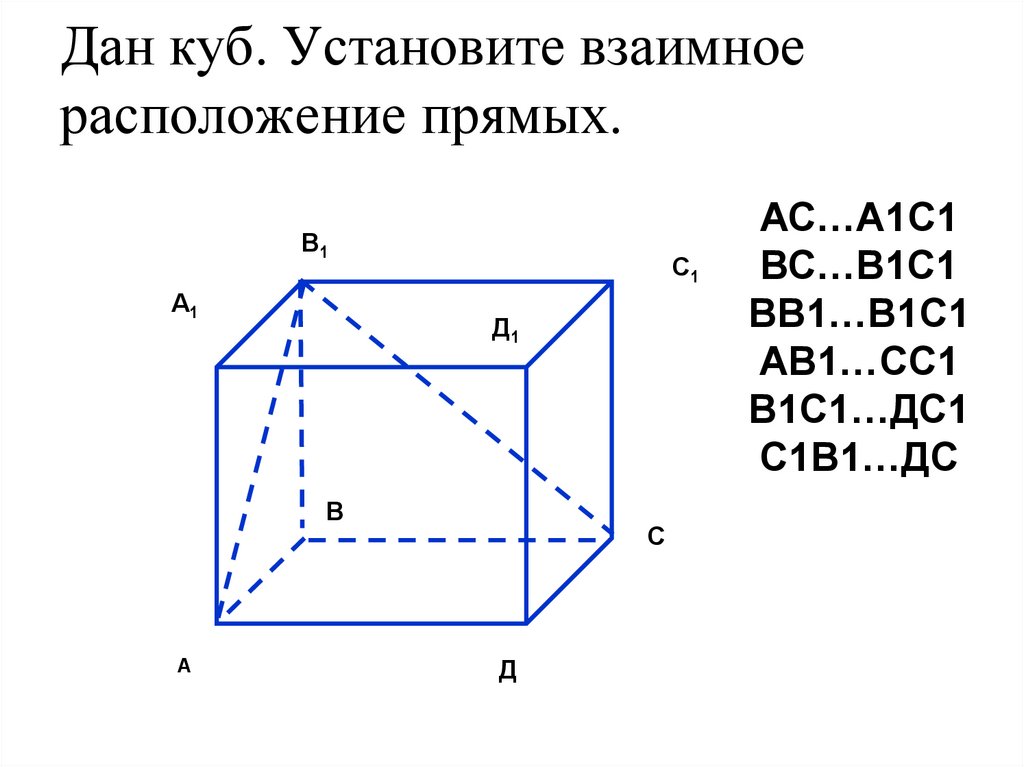
6. Дан куб. Установите взаимное расположение прямых.
В1А1
С1
Д1
В
А
С
Д
АС…А1С1
ВС…В1С1
ВВ1…В1С1
АВ1…СС1
В1С1…ДС1
С1В1…ДС
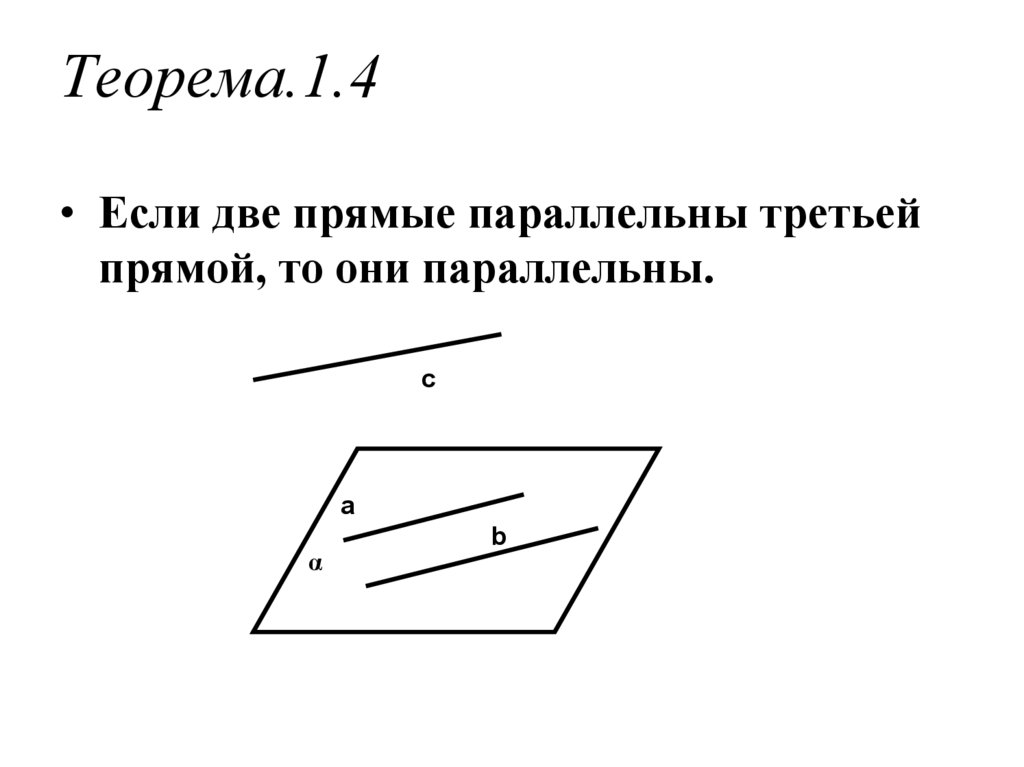
7. Теорема.1.4
• Если две прямые параллельны третьейпрямой, то они параллельны.
c
а
α
b
8. Теорема1.5
• Если прямая, не лежащая в данной плоскостипараллельна какой-нибудь прямой, лежащей
в этой плоскости, то она параллельна данной
плоскости.
а
b
α
9. Утверждение
1. Если плоскость проходит через даннуюпрямую, параллельную другой плоскости, и
пересекает эту плоскость, то линия
пересечения плоскостей параллельна данной
прямой.
2. Если одна из двух параллельных прямых
параллельна данной плоскости, то другая
прямая либо также параллельна данной
плоскости, либо лежит в этой плоскости.
10.
Взаимное расположениепрямой и плоскости
11.
a и bДа
Имеют хотя
бы одну
общую
точку
Да
a є b
Имеют
более
одной
общей
точки
Нет
Нет
a || b
a ∩b
12. Определение
• Прямая и плоскостьназываются
параллельными, если они
не имеют общих точек.
13. Тема урока
Скрещивающиеся прямые.Угол с сонаправленными
сторонами.
Угол между прямыми
14. Теорема 1.6
Если одна из двух прямых лежит внекоторой плоскости, а другая прямая
пересекает эту плоскость в точке, не
лежащей на первой прямой, то эти
прямые скрещивающиеся. D
В
А
α
С
15. Теорема 1.7
Через каждую из двух скрещивающихсяпрямых проходит плоскость,
параллельная другой прямой, и притом
только одна.
С
А
Д
Е
В
α
16. Определение
Два луча ОА и О1А1, нележащие на одной прямой,
называются
сонаправленными, если они
параллельны и лежат в одной
полуплоскости с границей
ОО1.
17. Теорема 1.8
Если стороны двух угловсоответственно сонаправлены, то
такие углы равны.
О
А
ААААААаа
Аа
В
А1
О1
В1
18. угол между прямыми АВ и СD равен γ
АА1
С1
γ
С
D
В
М1
D1
В1
















 mathematics
mathematics








