Динамика твердого тела

1.

Динамика твердого
тела
Задание по физике для групп 711, 712.
На этой неделе тема лекции Динамика твердого
тела. Делаем соответствующие задания из тестов
Ответы и вопросы присылать на почту
[email protected] в течение недели
Вопросы

2.

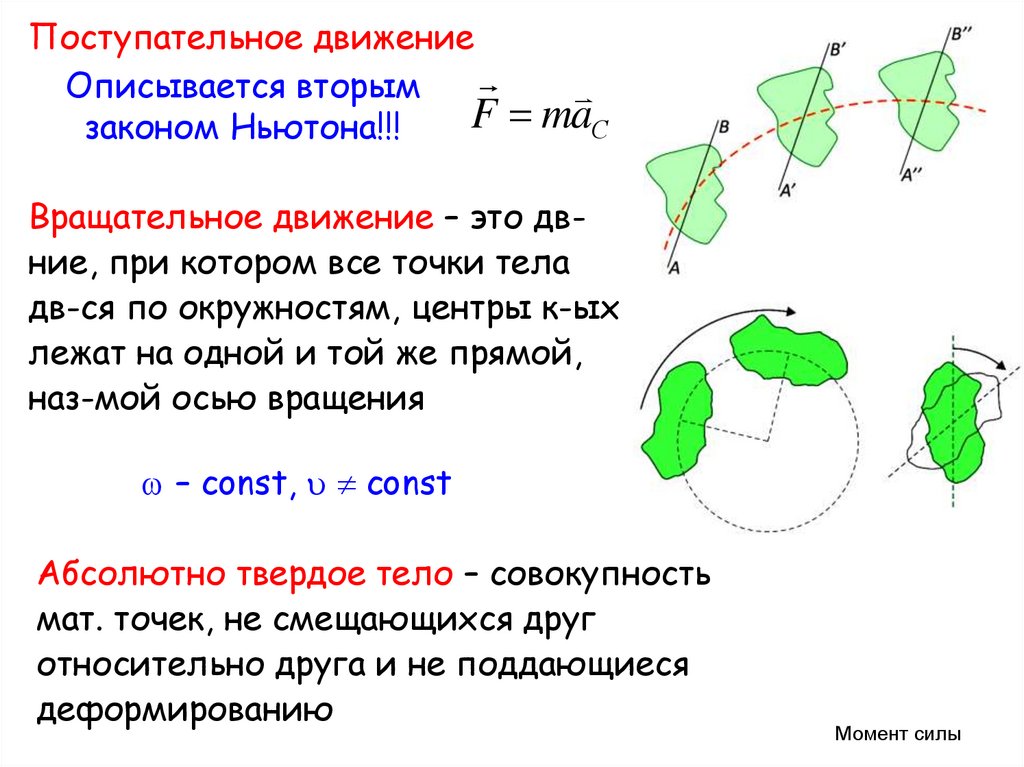
Поступательное движение
Описывается вторым
F
законом Ньютона!!!
maС
Вращательное движение – это двние, при котором все точки тела
дв-ся по окружностям, центры к-ых
лежат на одной и той же прямой,
наз-мой осью вращения
– const, const
Абсолютно твердое тело – совокупность
мат. точек, не смещающихся друг
относительно друга и не поддающиеся
деформированию
Момент силы

3.

F||
O’
r
Fвр
O
F
F Fвр F F||
F
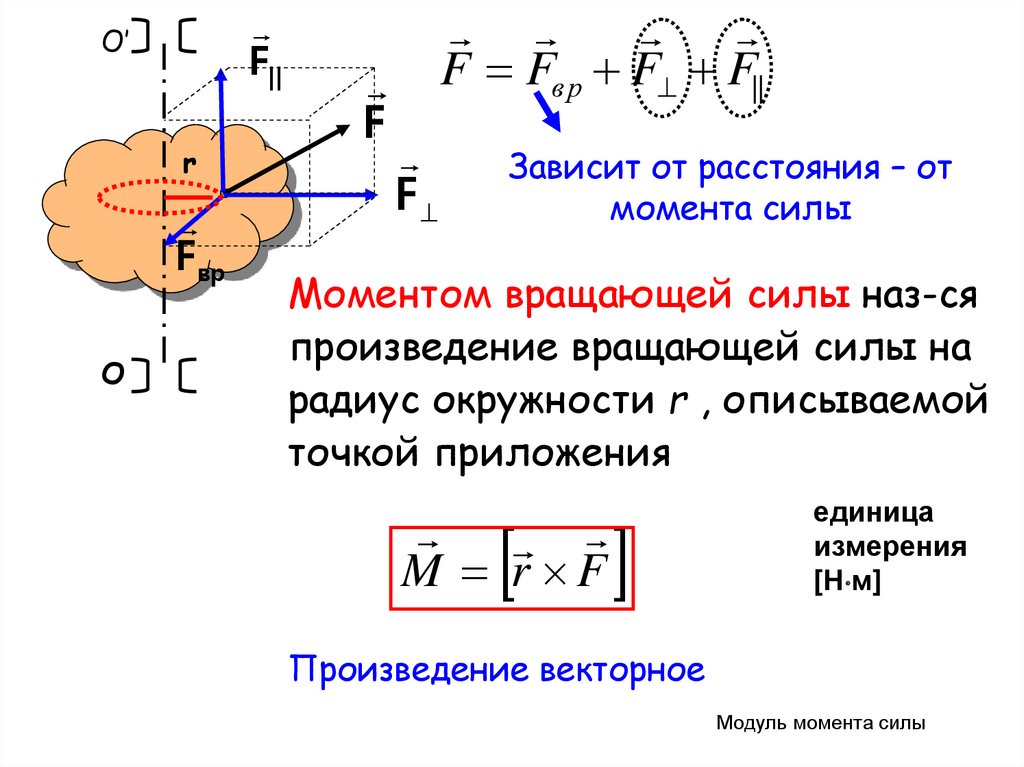
Зависит от расстояния – от
момента силы
Моментом вращающей силы наз-ся
произведение вращающей силы на
радиус окружности r , описываемой
точкой приложения
M r F
единица
измерения
[Н м]
Произведение векторное
Модуль момента силы

4.

F||
O
’
r
Fвр
O
F
M r F
F
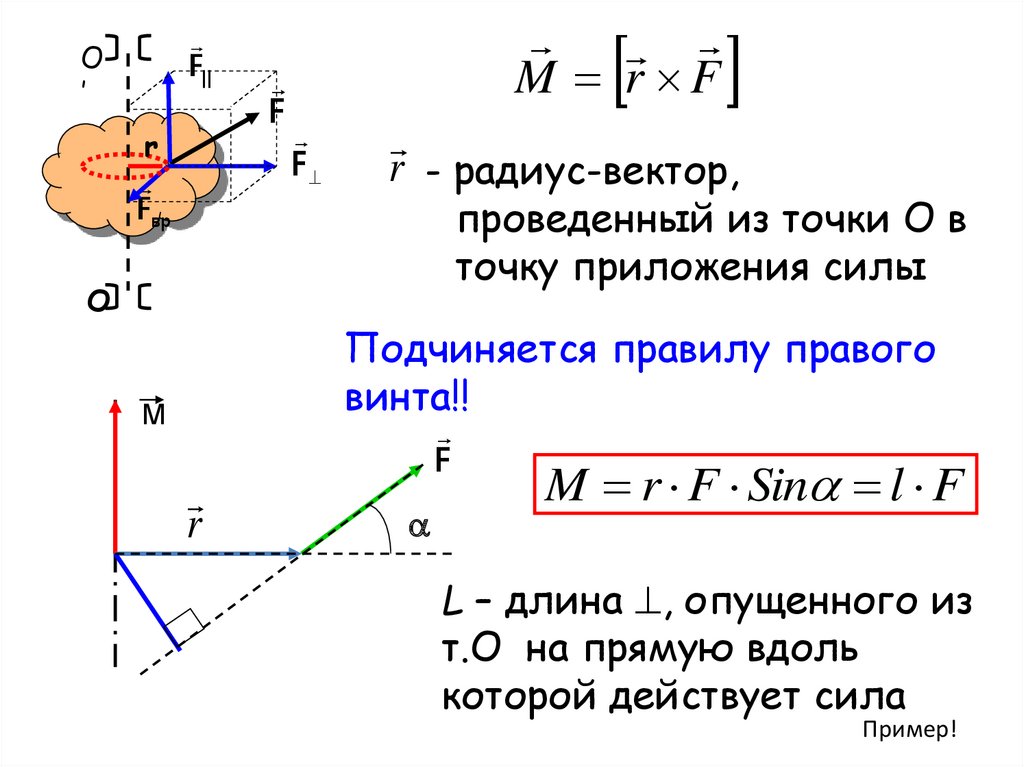
r - радиус-вектор,
проведенный из точки О в
точку приложения силы
Подчиняется правилу правого
винта!!
М
r
F
M r F Sin l F
L – длина , опущенного из
т.О на прямую вдоль
которой действует сила
Пример!

5.

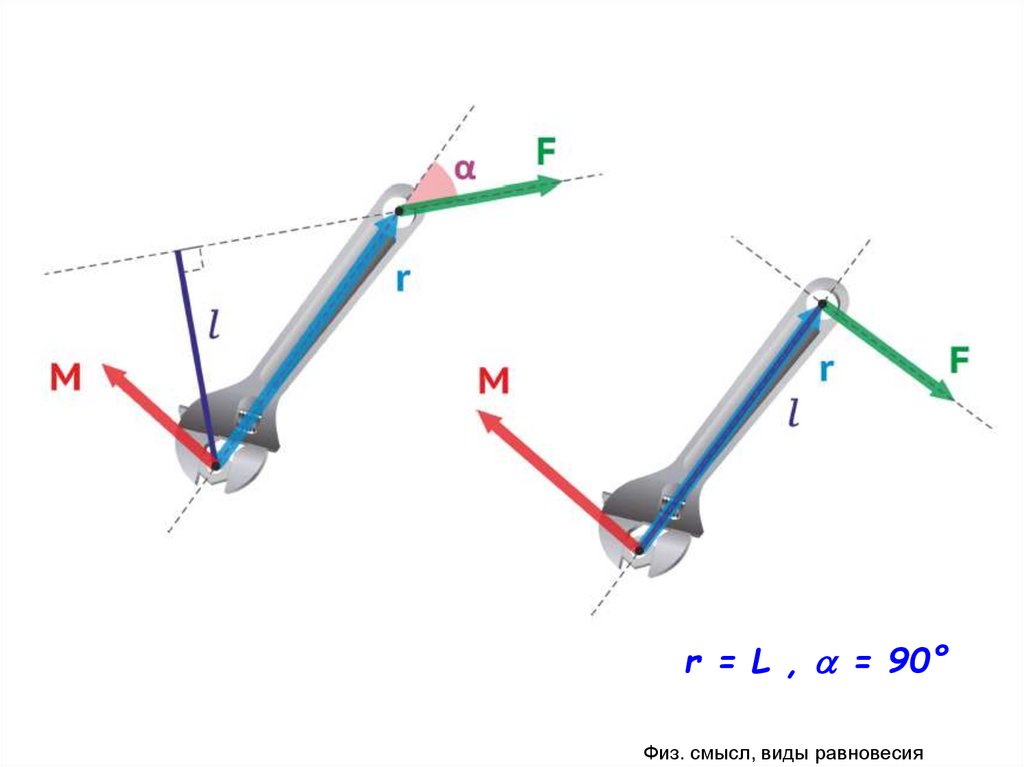
r = L , = 90°
Физ. смысл, виды равновесия

6.

1.
Fi 0 обеспечивает неподвижность
центра масс (если тело покоилось в
начальный момент времени)
i
M
0
i
2.
обеспечивает отсутствие
i
вращательного движения тела
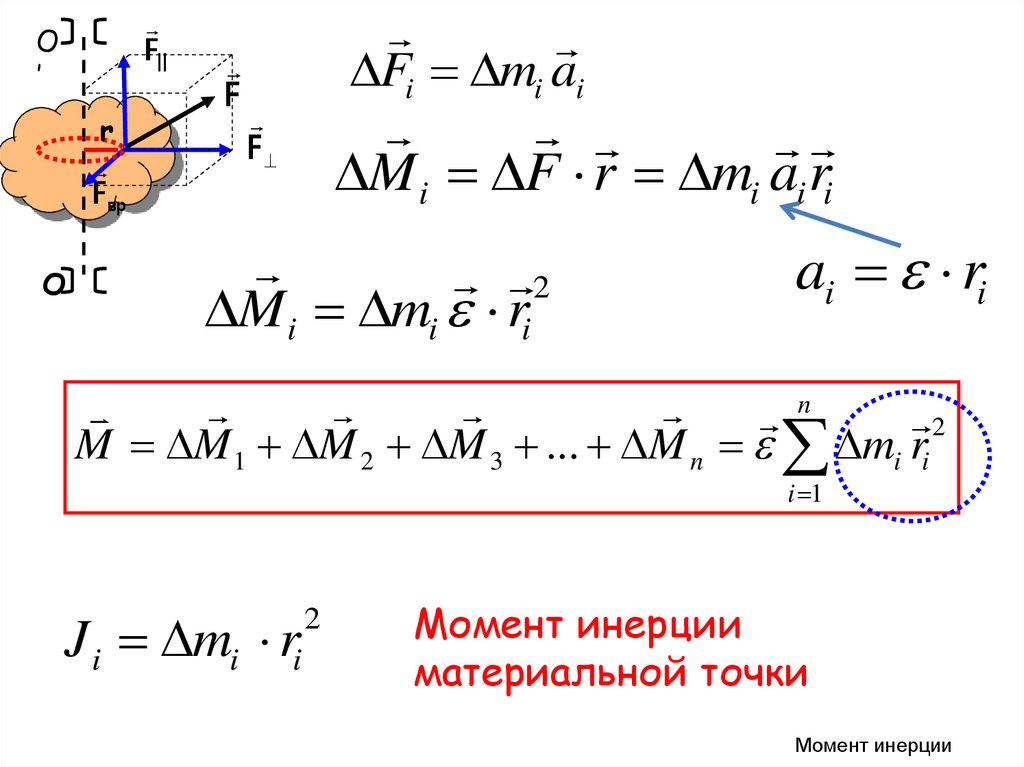
Элементарный момент силы

7.

F||
O
’
r
Fвр
O
F
Fi mi ai
M i F r mi ai ri
F
2
M i mi ri
ai ri
n
2
M M 1 M 2 M 3 ... M n mi ri
i 1
J i mi ri
2
Момент инерции
материальной точки
Момент инерции

8.

Момент инерции тела– величина, равная сумме
произведений элементарных масс тела на
квадрат их расстояний от оси вращения.
n
J mi ri
i 1
2
n
J Ji
J=
[кг м2]
i 1
Момент инерции тела – сумма инерций всех
материальных точек, составляющих данное тело
M J
Момент вращающей силы, приложенной к телу
равен произведению момента инерции данного
тела на угловое ускорение – основной закон
Инерция и масса - сравнение
динамики вращ. дв-ния

9.

M J
По аналогии
F maС
Момент инерции масса тела
Тело обладает моментом инерции независимо
от того, вращается оно или нет.
J1 J 2
1 2
Разница между
массой и моментом
инерции – масса
тела не
изменяется!!!,
Момент инерции можно
изменить перемещением
масс относительно оси
вращения
Момент импульса

10.

M J
Mdt Jd
d
dt
If J = const
d
M J
dt
Mdt d ( J )
Момент импульса хар-ет количество
вращательного движения.
dL
M
dt
по форме напоминает
L
dp
F
dt
Момент силы определяет скорость
изменения момента импульса
Сохранение момента импульса

11.

В замкнутой системе
M 0
L const
dL
0
dt
J const
Если на систему не действуют внешние силы или
сумма этих моментов равна нулю, либо силы
являются центральными, то момент количества
движения системы остается постоянным – закон
сохранения момента импульса замкнутой
системы.
Актуально для решения задач!
Вычисление момента инерции

12.

J r dm ( r )dV
2
Для однородных тел геометрически правильной
формы → интегрированием
Для неоднородных тел и тел неправильной формы →
экспериментально
Тонкий стержень длиной l
l
l
3
l
J r S dr S r dr S
3
0
0
2
ml
J
3
2
2
2
ml
J
12
Зависит от
положения оси
вращения!
От массы Шар, цилиндр

13.

Через центр фигуры
Шар
2
2
J mR
5
Сферическая
оболочка
2
2
J mR
3
Совпадает с осью цилиндра
Полый тонкостенный
Сплошной цилиндр
цилиндр радиуса R
радиуса R
1
2
J mR
2
J mR
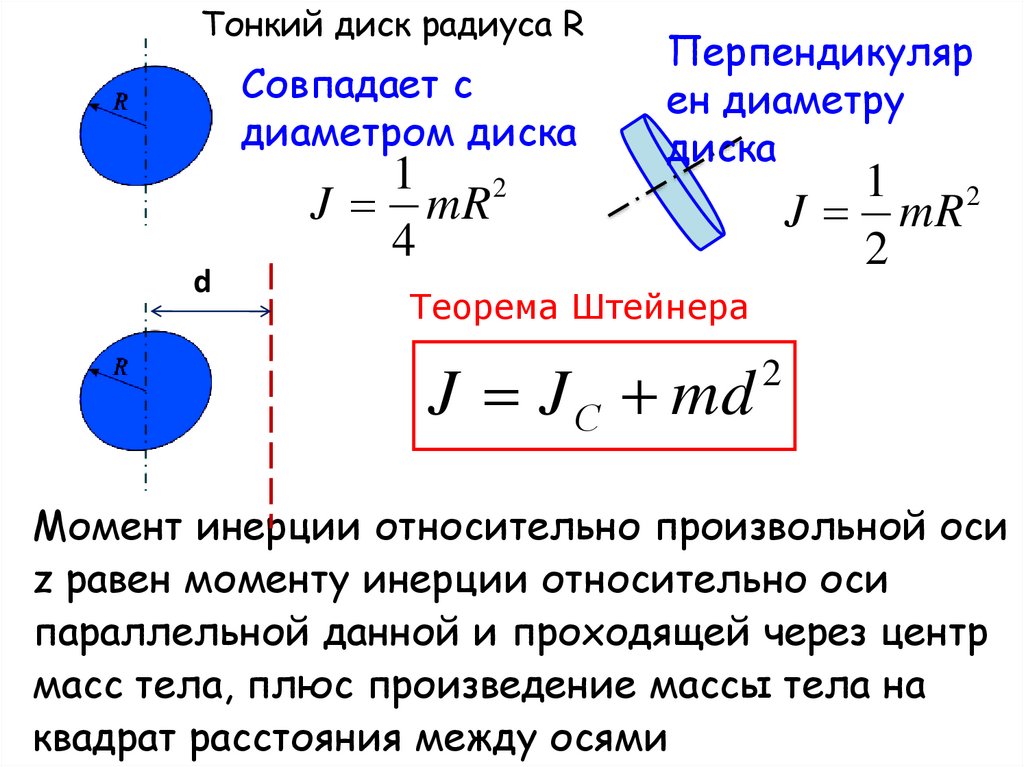
Диск, теорема Штейнера
2

14.

Тонкий диск радиуса R
Совпадает с
диаметром диска
1
2
J mR
4
d
Перпендикуляр
ен диаметру
диска
1
2
J mR
2
Теорема Штейнера
J J С md
2
Момент инерции относительно произвольной оси
z равен моменту инерции относительно оси
параллельной данной и проходящей через центр
масс тела, плюс произведение массы тела нa
квадрат расстояния между осями

15.

Тонкий стержень длиной R
Перпендикулярно стержню и
проходит через его середину
ml 2
J
12
d
Новая ось // и проходит через его
конец
2
2
2
2
ml
ml
ml
4ml
ml
2
J
md
12
12
4
12
3
d l /2
Кинетическая энергия
2

16.

Полная кинетическая энергия тела равна
сумме кинетической энергии его частиц
Eкин
n
1 n
1
2
2
mi i mi ri
2 i 1
2 i 1
r
n
= const
Eкин
1 2
1 2
2
mi ri J
2
2
i 1
Если 2 движения – поступательное и вращательное
Eкин
1 2
1
J C m 2
2
2
Кинетическая энергия представляет собой сумму
кинетических энергий вращения тела относительно оси,
проходящей через центр масс, плюс кинетическая
пример колесо
энергия поступательного движения Формулировка,
центра масс.

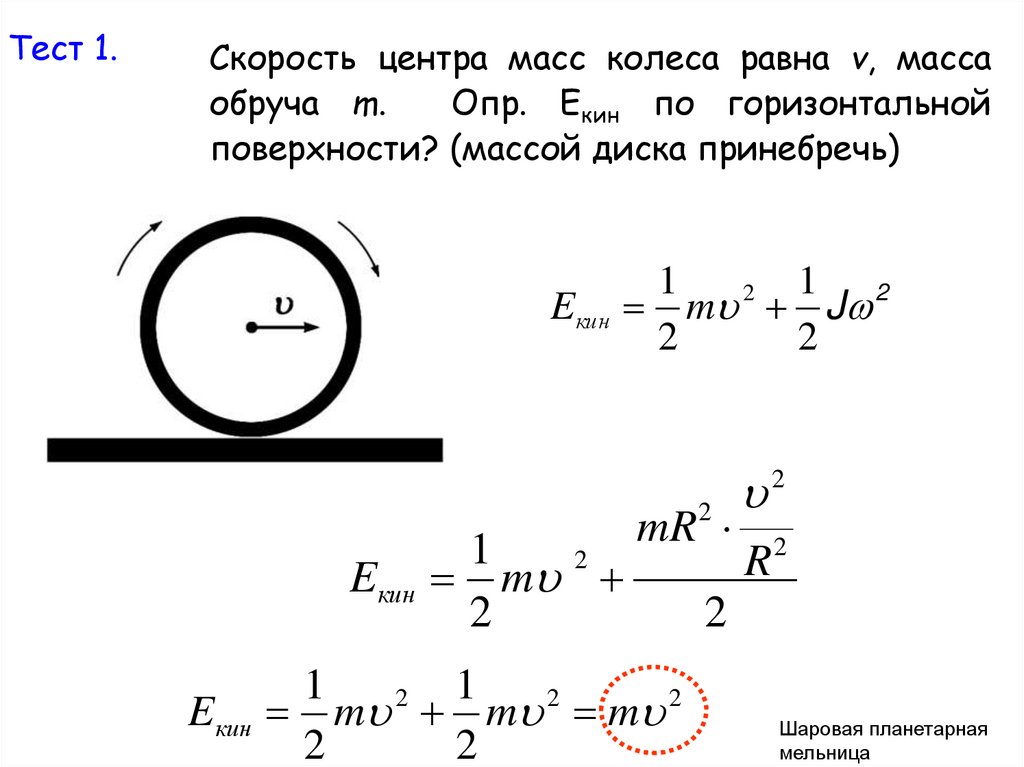
17.

Тест 1.
Скорость центра масс колеса равна v, масса
обруча m.
Опр. Eкин по горизонтальной
поверхности? (массой диска принебречь)
Eкин
1
1 2
2
m J
2
2
mR
2
Eкин
Eкин
1
2
m
2
1
1
2
2
2
m m m
2
2
2
R
2
2
Шаровая планетарная
мельница

18.

Шаровые планетарные мельницы
Частица глюконата
кальция после 30 минут
измельчения.
Скорость растворения
увеличивается в 2000
раз!!
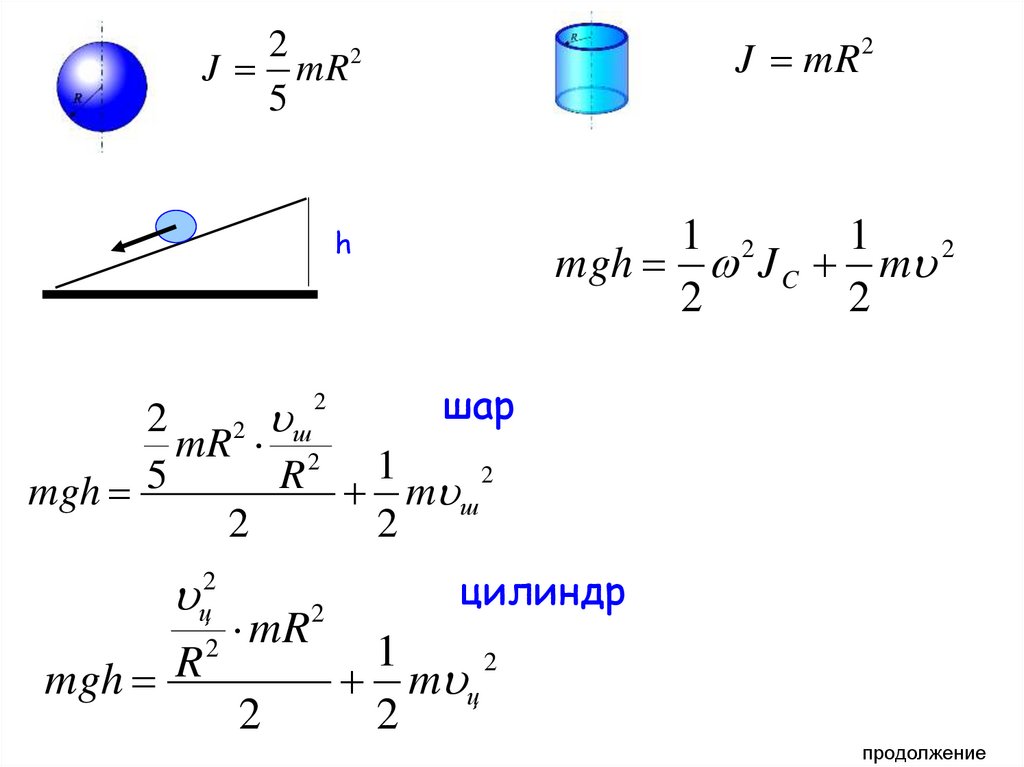
Маховик, задачка на шар
и цилиндр

19.

2
J mR 2
5
h
J mR 2
1 2
1
mgh J C m 2
2
2
2
шар
2
mR2 ш2
1
1
1
7
2
2
2
2
5
R
mgh
m ш m ш m ш m ш
2
2
5
2
10
2
ц
2
mgh R
mR
2
2
цилиндр
1
1
1
2
2
2
2
m ц m ц m ц m ц
2
2
2
продолжение

20.

0,7m ш m ц
2
2
ш
ц
0,7
1,19 ц
ш ц
2
J mR 2
5
Меньше момент инерции → выше
скорость!!!!
J mR
Опр. высоту
2

21.

2
J mR 2
5
J mR
2
ш ц
1 2
1
2
mgh I C m
2
2
h
шар
mghш Eкин
7
m
10
цилиндр
mghц Eкин m
2
2
hш 7
hц 10
hш 0,7hц
Больше момент инерции
больше высота!!!!