Similar presentations:
Динамика вращательного движения твердого тела. Лекция 5
1. Динамика вращательного движения твердого тела
Лекция №52. План лекции
• 1. Движение твердого тела (плоское движение).• 2. Момент силы. Момент импульса. Основной
закон динамики вращательного движения.
• 3. Момент инерции. Теорема Штейнера.
• 4. Кинетическая энергия твердого тела при
плоском движении.
• 5. Закон сохранения момента импульса.
3. 1. Движение твердого тела (плоское движение)
4.
• Любое тело можно представить как систему материальных точек. Еслирасстояние между этими точками остается неизменным, при действии
любых сил, то такое тело называют абсолютно твердым.
• Поступательным называют движение тела, при котором любая прямая,
связанная с телом, перемещается параллельно самой себе.
• Вращательным движением твердого тела называется движение при
котором все его точки движутся по окружностям, центры которых лежат
на одной прямой, называемой осью вращения.
• Плоским движением называется
движение точки, если ее траектория
плоская кривая, т.е. траектория
целиком лежит в одной плоскости.
5.
2. Момент силы. Момент импульса.Основной закон динамики
вращательного движения
6.
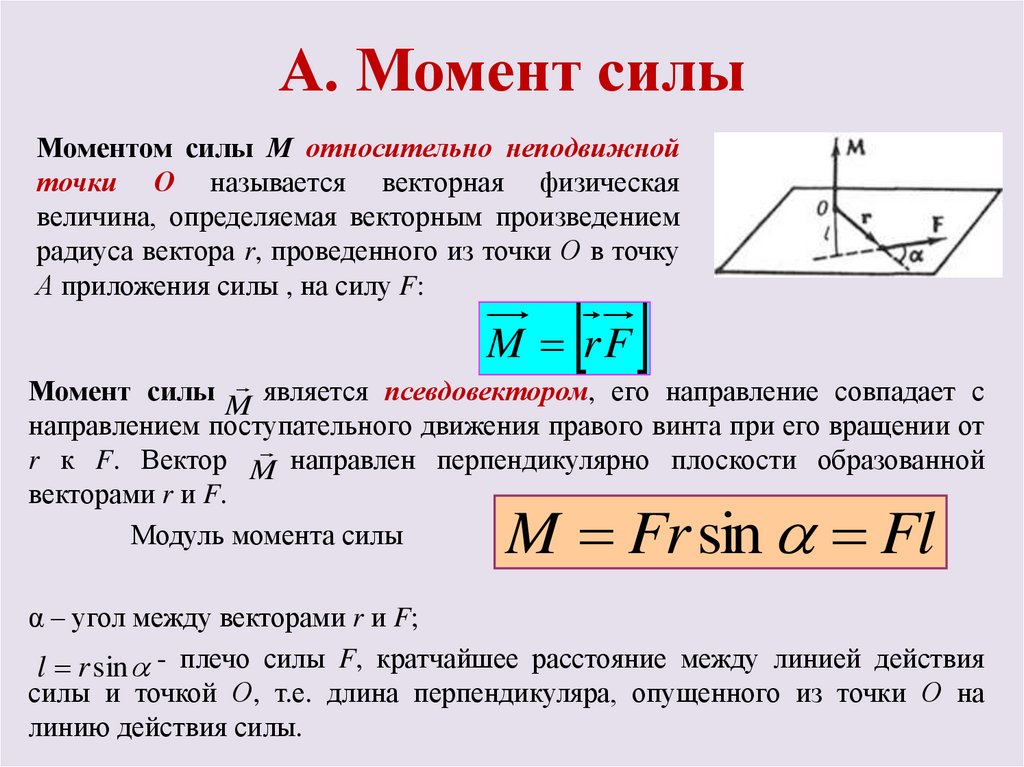
А. Момент силыМоментом силы М относительно неподвижной
точки О называется векторная физическая
величина, определяемая векторным произведением
радиуса вектора r, проведенного из точки О в точку
А приложения силы , на силу F:
M rF
Момент силы является псевдовектором, его направление совпадает с
M
направлением поступательного движения правого винта при его вращении от
направлен перпендикулярно плоскости образованной
r к F. Вектор M
векторами r и F.
Модуль момента силы
M Fr sin Fl
α – угол между векторами r и F;
l r sin - плечо силы F, кратчайшее расстояние между линией действия
силы и точкой О, т.е. длина перпендикуляра, опущенного из точки О на
линию действия силы.
7. 2. Момент силы. Момент импульса. Основной закон динамики вращательного движения
Б. Момент импульсаМоментом импульсаLi
м.т. А относительно
неподвижной точки О называется векторная
физическая величина, определяемая векторным
r
произведением
радиуса-вектора i
м.т.,
проведенного из точки
О, на импульс этой
материальной точки pi :
Li ri pi
ri - радиус-вектор, проведенный из точки О в точку А;
pi mi i - импульс материальной точки.
Момент импульса Li является псевдовектором, его направление совпадает
pi
с направлением правого винта при его вращении от
к . ri
Модуль вектора момента импульса
Li ri pi sin mi i ri sin
p
α – угол между векторами ri и i .
8. А. Момент силы
В. Основной закон динамикивращательного движения
• Вектор, равный геометрической сумме моментов относительно
неподвижной точки О всех внешних сил, действующих на механическую
систему, называется главным моментом внешних сил относительно
неподвижной точки О:
n
внеш
внеш
M
ri Fi
i 1
• Получаем основное уравнение динамики вращательного движения
(ОУДВД) твердого тела:
dL внеш
M
dt
• Скорость изменения момента импульса механической системы
относительно неподвижной точки (оси) равна главному моменту всех
внешних сил, действующую на систему относительно той же точки (оси).
9.
3. Момент инерции. ТеоремаШтейнера
10. Б. Момент импульса
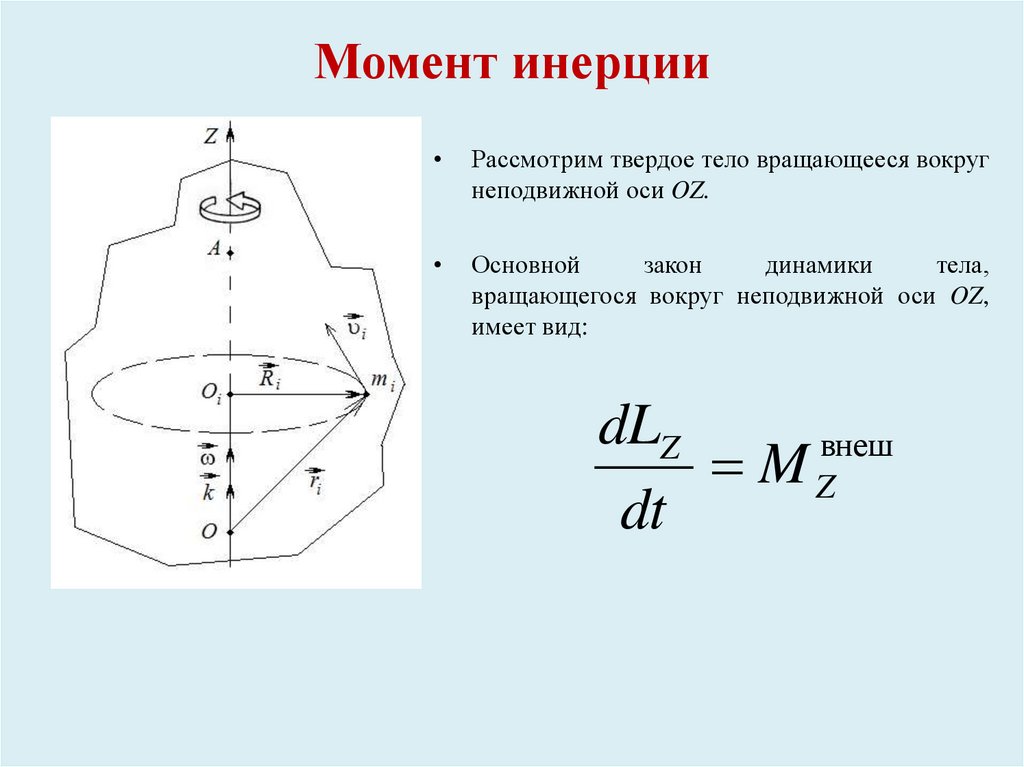
Момент инерцииРассмотрим твердое тело вращающееся вокруг
неподвижной оси OZ.
Основной
закон
динамики
тела,
вращающегося вокруг неподвижной оси OZ,
имеет вид:
dLZ
внеш
MZ
dt
11.
• Величина, равная сумме произведений масс всех материальных точек,образующих механическую систему, на квадраты их расстояний от данной
оси вращения, называется моментом инерции системы относительно этой
оси:
n
I mi Ri2
i 1
• Таким образом, момент импульса тела относительно оси OZ равен
Ι mi ri
2
• где I – момент инерции тела относительно оси вращения OZ.
• Если известен закон распределения массы тела, то момент инерции
твердого тела можно определить по формуле:
LZ I
• Моментом инерции м.т. относительно некоторой оси называют
скалярную физическую величину, равную произведению массы
материальной точки на квадрат расстояния до оси вращения: I r 2 dm
12.
• УравнениеdLZ
M Zвнеш с учетом
dt
LZ I можно записать в виде:
d
I Z M Zвнеш
dt
• В процессе вращения считается, что I=const, т.е. тело не деформируется
или
I
d Z
M Zвнеш
dt
I Z M Zвнеш
• Из уравнения видно, что угловое ускорение обратно пропорционально
моменту инерции. Следовательно, момент инерции тела относительно
оси является мерой инертности тела в его вращении вокруг этой оси.
внеш
M
I
- основное уравнение динамики вращательного
движения
13.
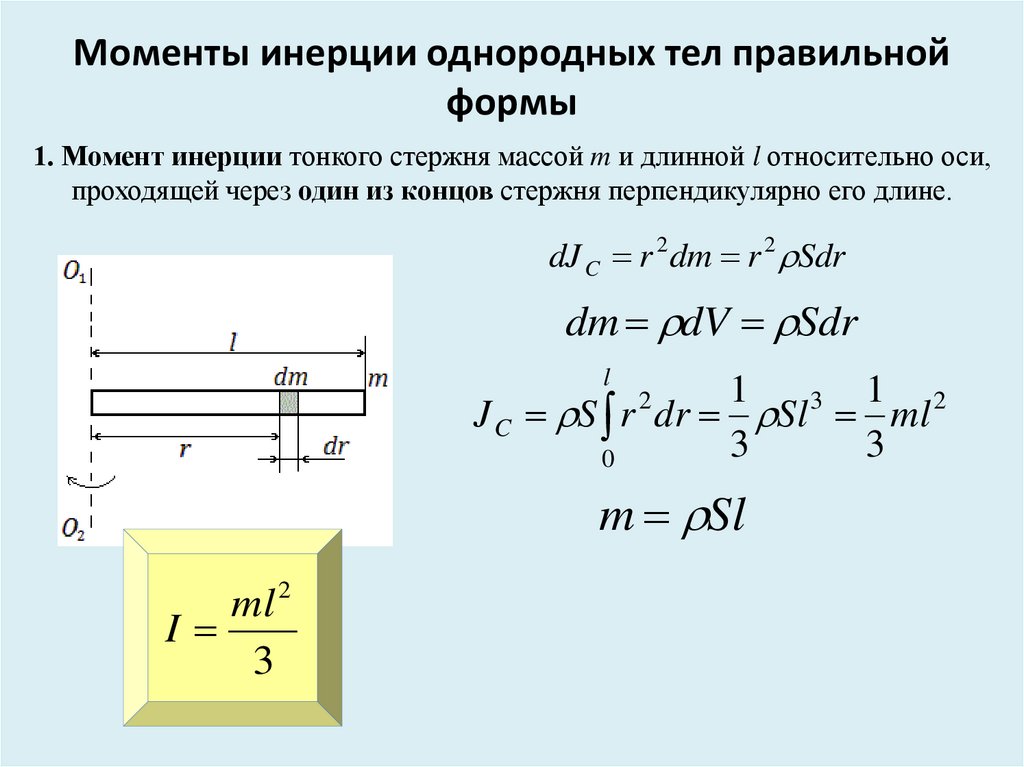
Моменты инерции однородных тел правильнойформы
1. Момент инерции тонкого стержня массой m и длинной l относительно оси,
проходящей через один из концов стержня перпендикулярно его длине.
dJ C r 2 dm r 2 Sdr
dm dV Sdr
l
1
1 2
3
J C S r dr Sl ml
3
3
0
2
m Sl
ml
I
3
2
14. 3. Момент инерции. Теорема Штейнера
Значения моментов инерции для некоторых тел(тела считаются однородными, m – масса тела)
Тонкое кольцо, материальная точка, полый
тонкостенный цилиндр (ось симметрии)
Сплошной цилиндр, диск (ось симметрии)
Диск (ось вращения проходит через диагональ)
J mR 2
1
J mR2
2
1
J mR2
4
Шар
2
J mR 2
5
Полая тонкостенная сфера
2
J mR 2
3
Прямой тонкий стержень длиной l,
перпендикулярна стержню и проходит через
середину
Прямой тонкий стержень длиной l,
перпендикулярна стержню и проходит через
конец
ось
его
ось
его
J
1 2
ml
12
1
J ml 2
3
15. Момент инерции
Моменты инерции однородных тел относительнопроизвольной оси
Теорема Штейнера:
Момент инерции тела относительно любой оси равен сумме момента
инерции относительно оси, параллельной данной и проходящей через
центр масс и произведение массы тела на квадрат расстояния между
осями.
I O I C md
2
16.
Покажем справедливость теоремы Штейнера на примере со стержнем:Применение теоремы Штейнера к расчету
момента инерции тонкого стержня массой m и
длинной l относительно оси, проходящей через
один из концов стержня перпендикулярно его
длине.
I IC
IC
l2
m
4
ml 2
12
ml 2 ml 2 ml 2
I
12
4
3
17.
4. Кинетическая энергиятвердого тела
при плоском движении
18. Моменты инерции однородных тел правильной формы
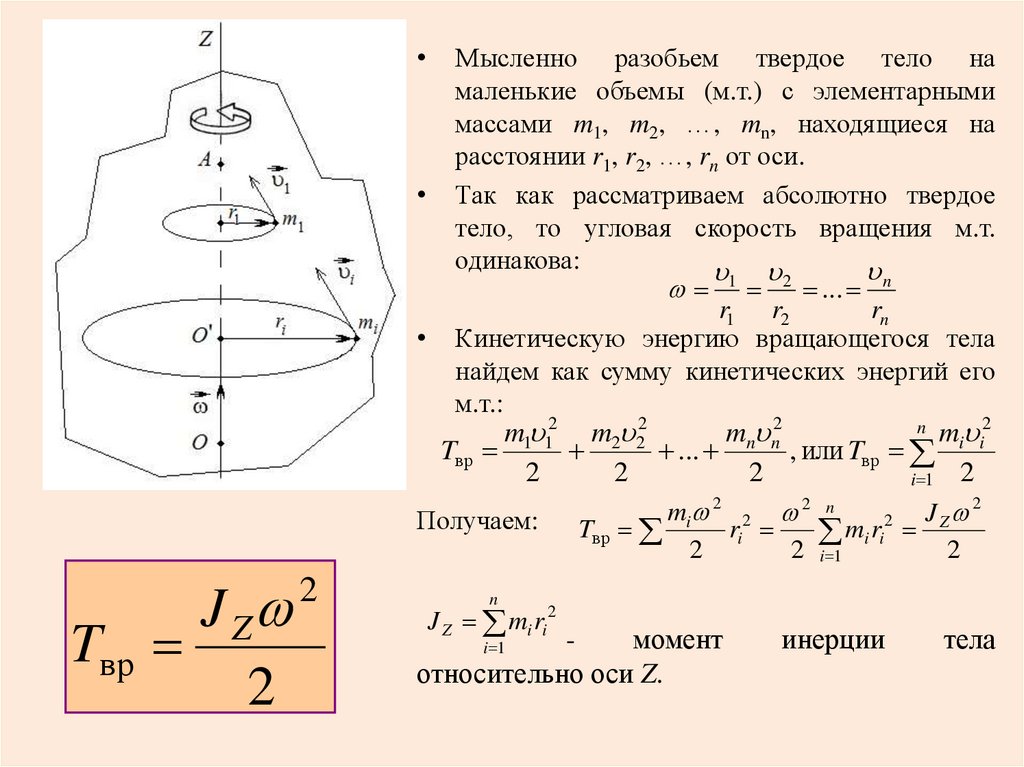
Мысленно разобьем твердое тело на
маленькие объемы (м.т.) с элементарными
массами m1, m2, …, mn, находящиеся на
расстоянии r1, r2, …, rn от оси.
• Так как рассматриваем абсолютно твердое
тело, то угловая скорость вращения м.т.
одинакова:
1 2 ... n
r1 r2
rn
• Кинетическую энергию вращающегося тела
найдем как сумму кинетических энергий его
м.т.:
n m 2
mn n2
m1 12 m2 22
Tвр
...
, или Tвр i i
2
2
2
i 1 2
2
2
2 n
m
J
2
2
i
Z
Получаем: T
ri
mi ri 2
вр
2
2 i 1
J Z
Tвр
2
2
n
J Z mi ri2
момент
относительно оси Z.
i 1
-
инерции
тела
19.
J Z 2
Tвр
2 - формула справедлива для тела, вращающегося вокруг
неподвижной оси.
• В случае плоского движения тела, например цилиндра, скатывающего с
наклонной плоскости без скольжения, энергия движущегося тела
складывается из энергии поступательного движения со скоростью, равной
скорости центра масс υС, и энергии вращения тела вокруг оси,
проходящей через центр тела:
m C2 J C 2
T
2
2
• где m – масса катящегося тела; υС – скорость центра масс тела; JС –
момент инерции тела относительно оси, проходящей через его центр
масс; ω – угловая скорость тела.
20.
Найдем работу при вращательномдвижении твердого тела
A = F dr = Fl = FR·d = M·d
A M d
Элементарная работа при
вращательном движении
A A M d
Работа при вращательном
движении
N
A Md
M
dt
dt
N M
- мощность при вращательном
движении
21.
5. Закон сохранения моментаимпульса
22. Значения моментов инерции для некоторых тел (тела считаются однородными, m – масса тела)
• Для замкнутой системы момент внешних сил Мвнеш всегдаравен нулю, так как на нее внешние силы не действуют.
• Из основного закона динамики вращательного движения
твердого тела
внеш
dL
M
dt
• вытекает закон сохранения момента импульса: момент
импульса
замкнутой
системы
относительно
неподвижной точки (оси) не изменяется с течением
времени.
dL
dt
внеш
dLC
MC
dt
0, L const
• Из уравнения
следует:
• момент импульса замкнутой системы относительно ее центра
масс не изменяется с течением времени
LC const
23.
• Момент импульса замкнутой системы относительно любойнеподвижной оси а также остается постоянным:
La const
• Закон сохранения момента импульса является фундаментальным
законом природы, который далеко выходит за рамки классической
механики.
• Закон сохранения момента импульса связан со свойством симметрии
пространства – его изотропностью, т. е. с инвариантностью физических
законов относительно выбора направления осей координат системы
отсчета.
• Моментом импульса обладают не только движущиеся макроскопические
тела и системы, но также и отдельные атомы, атомные ядра и
элементарные частицы.
• Атомные ядра имеют моменты импульса, не связанные с их движением в
пространстве.
24.
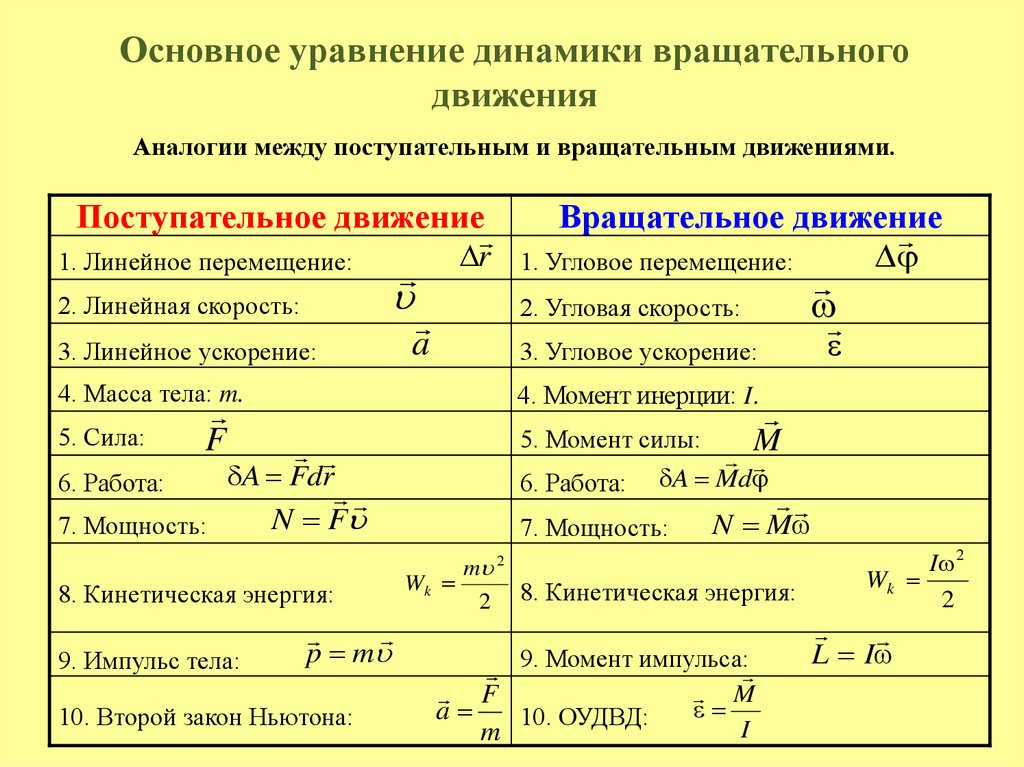
Основное уравнение динамики вращательногодвижения
Аналогии между поступательным и вращательным движениями.
Поступательное движение
1. Линейное перемещение:
2. Линейная скорость:
3. Линейное ускорение:
a
Вращательное движение
r 1. Угловое перемещение:
2. Угловая скорость:
3. Угловое ускорение:
4. Масса тела: m.
4. Момент инерции: I.
5. Сила:
5. Момент силы:
F
6. Работа:
A Fdr
7. Мощность:
N F
8. Кинетическая энергия:
9. Импульс тела:
p m
10. Второй закон Ньютона:
6. Работа:
M
A Md
7. Мощность:
N M
m 2
Wk
2 8. Кинетическая энергия:
9. Момент импульса:
M
F
a
10. ОУДВД:
I
m
I 2
Wk
2
L I



















 physics
physics








