Similar presentations:
Динамика движения твердого тела
1. Лекция № 6 ДИНАМИКА ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
1. Динамика вращательного движения относительноточки.
2. Динамика вращательного движения относительно
неподвижной оси.
3. Расчет моментов инерции некоторых простых тел.
Теорема Гюйгенса-Штейнера.
4. Закон сохранения момента импульса.
5. Кинетическая энергия твердого тела
6. Произвольное движение твердого тела.
7. Скатывание цилиндра с наклонной плоскости.
8. Сходство и различие линейных и угловых
характеристик движения.
.
2. 1. Динамика вращательного движения твердого тела относительно точки
Абсолютно твердое тело – это системаматериальных
точек,
расстояния
между
которыми сохраняются независимо от внешних
воздействий. Иными словами в твердом теле
отсутствует относительное движение этих
точек.
Рассмотрим твердое тело, как некую систему, состоящую
из n точек (m1 m2 … mn); ri – радиус-вектор i-ой точки,
проведенный из точки О –
неподвижного центра вращения.
обозначения:
действующая на
F - внешняя сила, действующая
на i-ю точку,
F - сила, действующая со
i
ik
стороны k-ой точки на i-ую
точку
3.
Запишем основное уравнение динамики для точки:d
m F F .
dt
n
i
i
ik
k 1
k i
i
Умножим обе части векторно на
r
i
d
r
,
m
dt
r , F r , F .
i
i
i
i
ik
k
i
i
Знак производной в данном случае можно вынести за
знак векторного произведения (и знак суммы тоже), тогда:
d
r , m r , F r , F .
dt
i
i
i
k
i
ik
i
i
4.
5.
6.
Векторное произведение вект.r, проведенного в точку
i
приложения силы, на эту силу называется моментом силы :
M i [ ri , Fi ]
По определению, модуль векторного произведения равен:
M i Fi ri sin
Обозначим ri sin li
li – плечо силы (перпендикуляр,
опущенный из неподвижной точки О на
линию действия силы). Тогда:
M i Fi ri sin Fi li
(произведение силы на плечо)
7.
C учетом новых обозначений наше уравнение:d
r , m r , F r , F .
dt
i
примет вид
i
i
i
k
ik
i
dL
M M
dt
i
n
i
ik
k 1
i
Запишем систему n уравнений для всех точек
системы и сложим, левые и правые части
уравнений:
dL
M M .
dt
n
n
n
i 1
k 1
n
i
i 1
Так как
F F
ik
ki
, то
ik
i
i 1
M 0.
n
n
i 1
k 1
ik
8.
Вынесем знак производнойза знак суммы
dL i d Li dL
dt
dt
i 1 dt
здесь L
- суммарный момент импульса
L
i
n
твердого тела.
Mi M
n
Обозначим
- результирующий
момент всех внешних
i 1
сил относительно неподвижной точки О.
Окончательно получим:
dL внеш
M
dt
9.
dLM
dt
Уравнение моментов
внеш
относительно неподвижной
точки
Это основной закон динамики движения твердого
тела, вращающегося вокруг неподвижной точки.
Имеет внешнее сходство с уравнением
динамики для поступательного движения:
внеш
dp
F
dt
Векторное уравнение можно представить
в
скалярном виде , если спроецировать L и M на
оси координат x, y, z:
dL x
внеш
Mx
dt
dL y
dt
My
внеш
dL z
внеш
Mz
dt
Написанные уравнения – уравнения моментов
относительно неподвижных осей.
10.
2. Динамика вращательного движения твердого телаотносительно неподвижной оси
При вращении твёрдого тела относительно
неподвижной оси, все точки тела движутся
по плоским круговым траекториям. Выделим
частицу mi тела, вращающегося вокруг оси z.
Положение
частицы
зададим
радиусвектором относительно произвольного
центра О, лежащего на оси вращения. Ri радиус окружности, по которой движется
рассматриваемая точка.
Будем рассматривать
угол поворота φ нашей
точки как вектор , имеющий модуль
направленный
вдоль
оси
вращения.
Направление вектора связано с направлением
вращения правилом буравчика. Аналогично
введем вектор угловой скорости и углового
ускорения
11.
Тогда вектор угловой скорости и вектор угловогоускорения будут выражаться
d
dt
2
d d
2
dt dt
Будем рассматривать проекцию момента импульса Liz
на ось вращения z и проекцию момента силы M iz на
ось вращения z. Назовем их моментом импульса
относительно оси z и моментом силы относительно
оси z.
12.
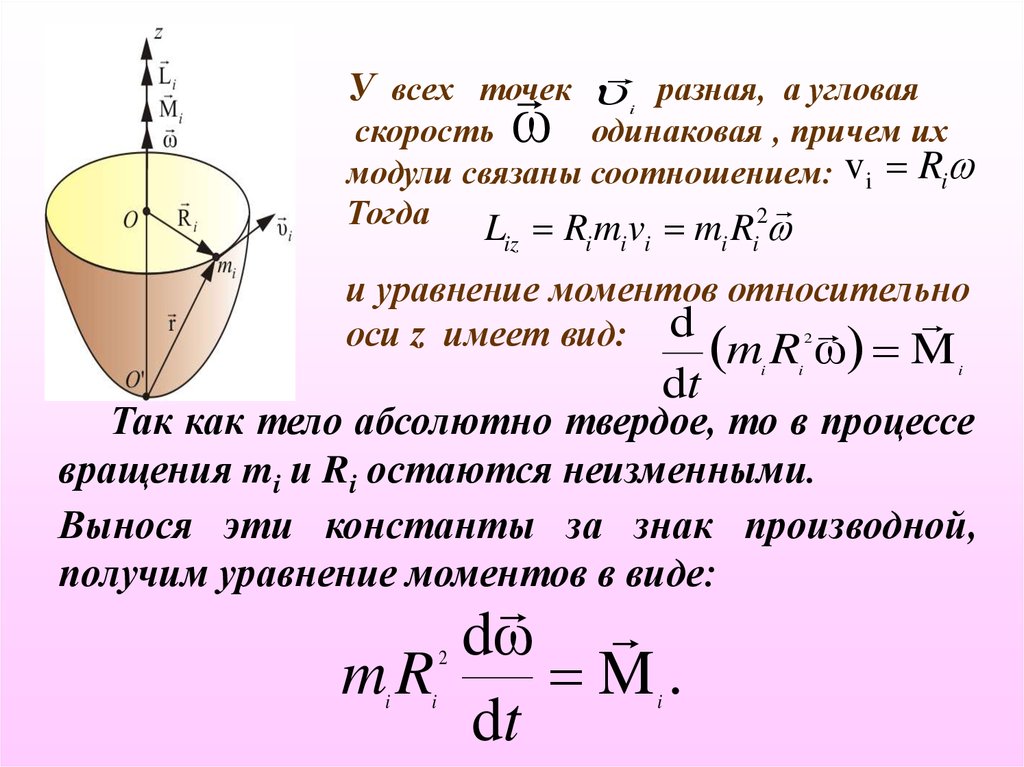
У всех точек разная, а угловаяскорость ω
i
одинаковая , причем их
модули связаны соотношением: v i Ri
2
Тогда
L Rmv m R
iz
i
i i
i
i
и уравнение моментов относительно
оси z имеет вид: d m R ω
M
2
dt
i
i
i
Так как тело абсолютно твердое, то в процессе
вращения mi и Ri остаются неизменными.
Вынося эти константы за знак производной,
получим уравнение моментов в виде:
dω
mR
M.
dt
2
i
i
i
13.
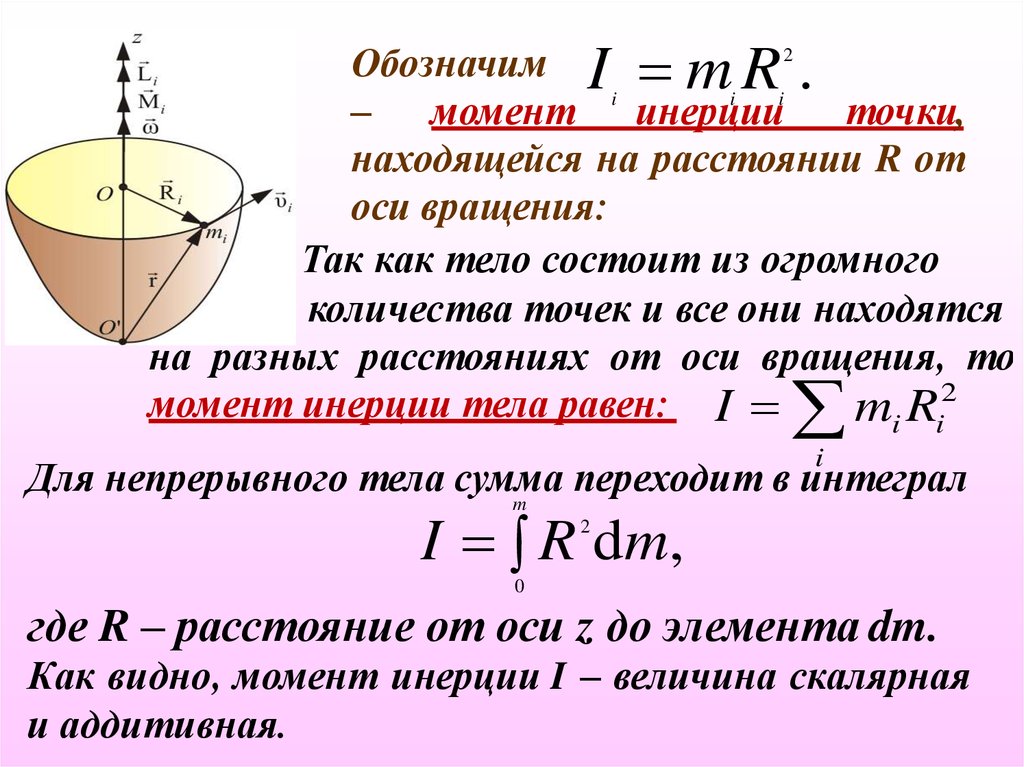
Обозначим I m R 2 .i
i
i
–
момент
инерции
точки,
находящейся на расстоянии R от
оси вращения:
Так как тело состоит из огромного
количества точек и все они находятся
на разных расстояниях от оси вращения, то
2
момент инерции тела равен: I
mi Ri
i
Для непрерывного тела сумма
переходит в интеграл
m
I R dm ,
2
0
где R – расстояние от оси z до элемента dm.
Как видно, момент инерции I – величина скалярная
и аддитивная.
14.
Просуммируем полученные для всех i-тых2 dω
точек уравнения моментов mi Ri
Mi
dt
Учтем, что I mi Ri2
i
dω
M
получим I
dt
или
Iε M
Это основное уравнение динамики тела
вращающегося вокруг
неподвижной оси.
(Сравним: ma F – основное уравнение
динамики поступательного движения
тела). Из сопоставления видно, что I
отображает инерционные свойства тела (по
отношению к данной оси вращения)
15.
.Момент импульса Li любой точки равен
Li = mirivi = miri ri = miri2
Момент импульса L твердого тела – это сумма
моментов импульсов всех его материальных точек
L Li mi ri 2 mi ri 2
i
Ранее мы получили, что
i
m r
i
i i
i
2
= I, поэтому окончательно
Для сравнения, в случае поступательного движения
16.
3.Расчет моментов инерции некоторыхпростых тел.
В качестве примера вычислим момент инерции тонкого
однородного стержня относительно оси z, проходящей через
его центр масс — точку С. Длина стержня — l, его масса —
M.
На расстоянии x от оси вращения выделим элемент dx,
масса которого dm M dx
l
Момент инерции этой
Z’
Z
частицы стержня равен:
X
C
x
0’
dx
X’
M
2
dI z
dx x
l
17.
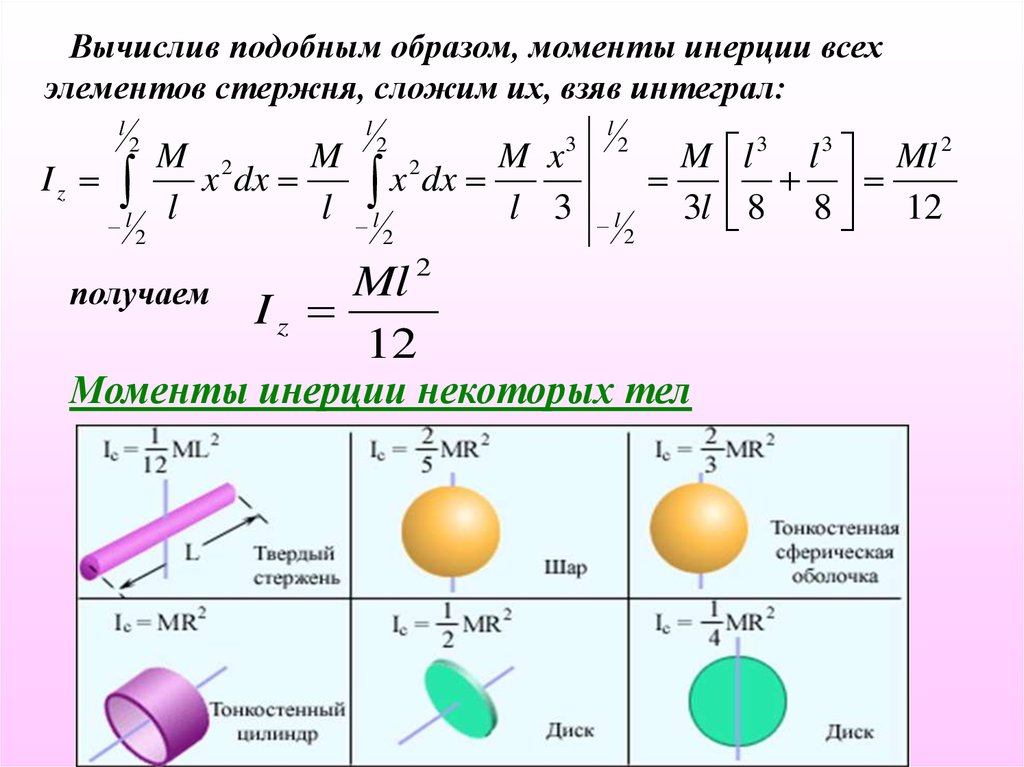
Вычислив подобным образом, моменты инерции всехэлементов стержня, сложим их, взяв интеграл:
l
Iz
2
l
l
M 2
M
x dx
l
l
2
получаем
3
2
M x
2
l x dx l 3
2
l
2
l
M
3l
2
2
Ml
Iz
12
Моменты инерции некоторых тел
l 3 l 3 Ml 2
8 8 12
18.
Теорема Гюйгенса-ШтейнераПри вычислении момента инерции тела,
вращающегося вокруг оси, не проходящей через
центр инерции, следует пользоваться теоремой о
параллельном переносе осей или теоремой Гюйгенса
- Штейнера :
Момент инерции тела
а
относительно произвольной оси (I)
равен сумме момента инерции Ic
относительно оси, параллельной
данной и проходящей через центр
масс тела, и произведения массы
тела М на квадрат расстояния
между осями:
I = Ic + Ma2
19.
Пример: стержень массой m,длиной l, вращается вокруг оси,
проходящей через конец стержня
(рис).
1
2
I c ml
12
2
1
1 2 1 2
l
I z I c m ml ml ml .
4
3
2 12
20.
4.Закон сохранения момента импульсаВернемся ещё раз к уравнению моментов в виде:
d
dLZ
M z I z z
dt
dt
Оно в равной степени справедливо как для твердого
тела, так и для системы тел. Если момент внешних
сил относительно оси z равен нулю, то момент
импульса системы относительно этой же оси будет
оставаться постоянным.
M z 0 dLz 0 Lz I z z const
dt
Это закон сохранения момента импульса — аналог
закона сохранения импульса.
21.
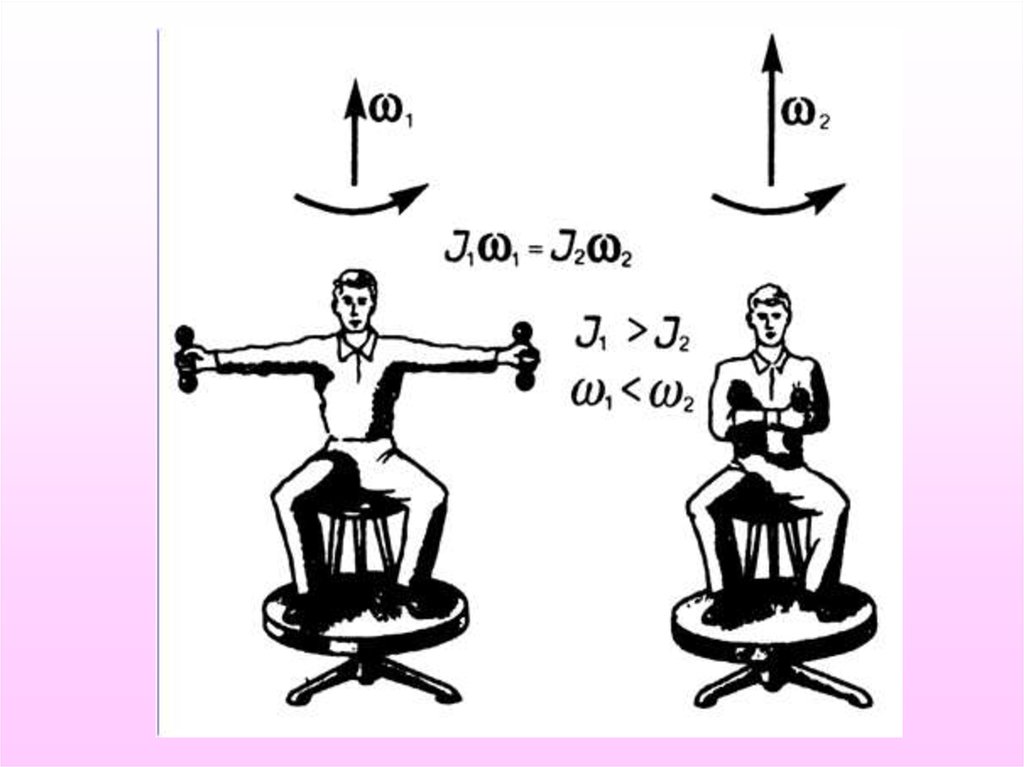
Lz I z z constЕсли не меняется момент импульса тела (Lz), то
это не означает постоянства угловой скорости:
если момент инерции вращающегося тела меняется,
то будет меняться его угловая скорость даже в
случае отсутствия внешних вращающих моментов.
При этом сохранится неизменным произведение
Iz = сonst, то есть угловая скорость
окажется обратно пропорциональной моменту
const
инерции тела (системы):
Iz
Известно много примеров, иллюстрирующих эту
особенность закона сохранения момента импульса:
вращение фигуристов и балерин, опыты на скамье
Жуковского и т.п.
22.
23.
5.Кинетическая энергия твердого телаВычислим кинетическую энергию К тела,
вращающегося вокруг неподвижной оси z с угловой
скоростью , суммируя кинетические энергии
бесконечно малых элементов тела
1
1
J
2
2 2
2
КК
T mi vi mi ri
mi ri
2 i
2 i
2 i
2
где J – момент инерции тела относительно оси
вращения тела, vi = riωi - линейная скорость
элемента тела с массой mi .
2
2
Сравним с формулой для кинетической энергии поступательного движения
K = mv2/2
24.
Произвольное движение твердого тела.Рассмотрим одно из простых движений абсолютно
твердого тела – плоское движение. Это движение ,
при котором все точки тела остаются в
параллельных плоскостях. Примером такого
движения является качение цилиндра по
горизонтальной или наклонной плоскостям.
Пусть тело движется под действием некоторой
системы внешних сил. Эту систему внешних сил
можно всегда привести к центру масс
тела О и
в неш
заменить результирующей силой F
, приложенной в точке О, и суммарным моментом внешних сил
внеш
относительно этой же точки M
o
25.
В результате полная система уравнений, описывающая произвольное движение абсолютно твердоготела, принимает вид:
где
m
- масса тела
0 - скорость движения центра масс тела и
L0 - момент импульса тела относительно его
центра масс.
26.
Кинетическаяэнергия
твердого
тела,
совершающего
поступательное движение
со
скоростью движения центра масс v0 и вращательное
движение с угловой скоростью
описывается
выражением:
m o I 0
K полн.
2
2
2
2
Здесь I0 – момент инерции относительно
мгновенной оси вращения, проходящей через
центр инерции.
27.
Условия равновесия абсолютно твердого телавключают два динамических условия
которые вытекают из уравнений движения, и два
кинематических условия
28.
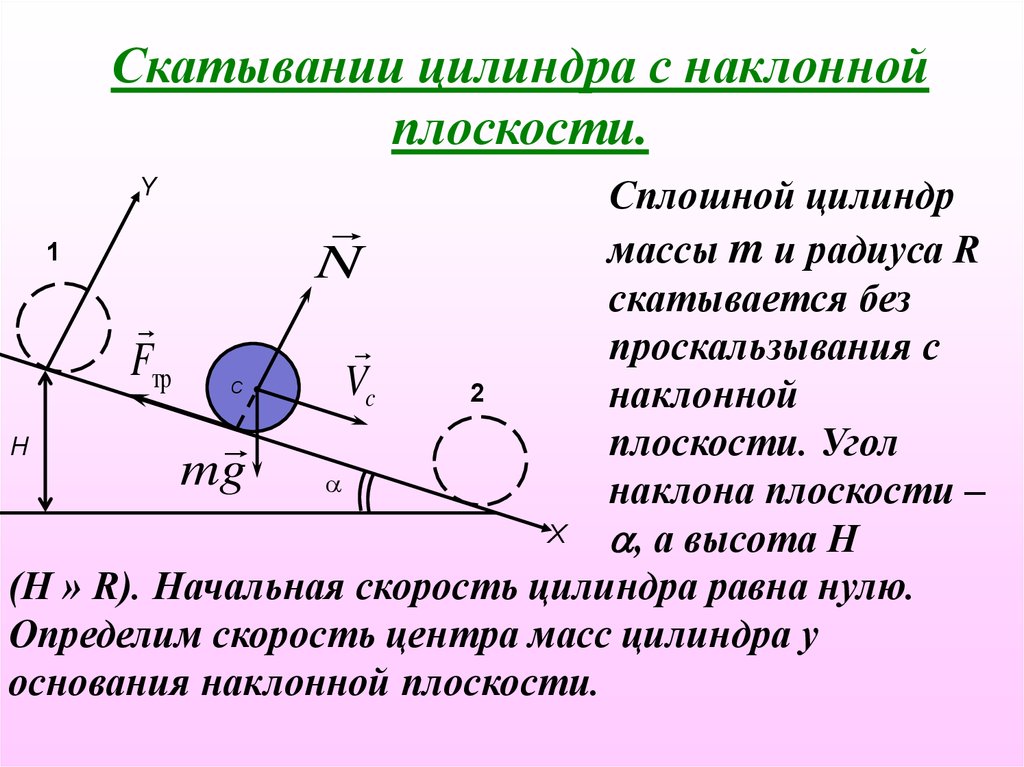
Скатывании цилиндра с наклоннойплоскости.
Сплошной цилиндр
1
массы m и радиуса R
N
скатывается без
проскальзывания с
Fтр C
Vc
2
наклонной
H
плоскости. Угол
mg
наклона плоскости –
X
, а высота Н
(Н » R). Начальная скорость цилиндра равна нулю.
Определим скорость центра масс цилиндра у
основания наклонной плоскости.
Y
29.
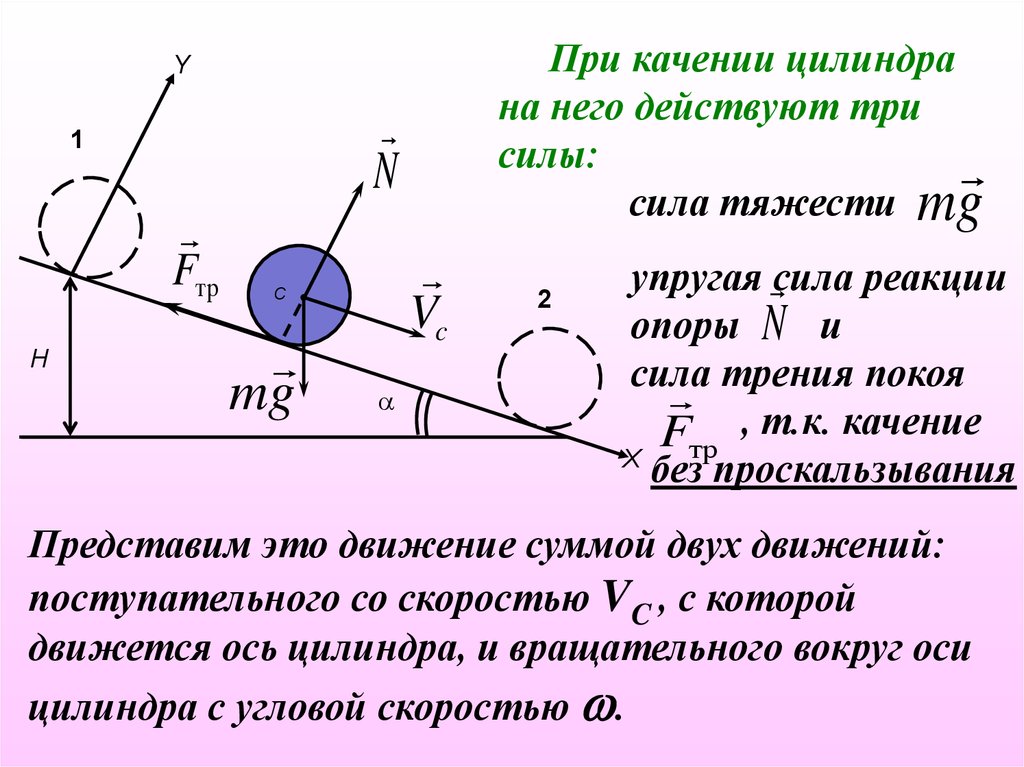
При качении цилиндрана него действуют три
силы:
сила тяжести mg
Y
N
1
Fтр
H
Vc
C
mg
2
упругая сила реакции
опоры N и
сила трения покоя
, т.к. качение
F
тр
X
без проскальзывания
Представим это движение суммой двух движений:
поступательного со скоростью VC , с которой
движется ось цилиндра, и вращательного вокруг оси
цилиндра с угловой скоростью .
30.
Эту задачу можно решить, воспользовавшисьзаконом сохранения механической энергии.
В системе, правда, присутствует сила трения, но
её работа равна нулю, поскольку точка приложения
этой силы в процессе спуска остаётся неподвижной:
ведь движение происходит без проскальзывания. Раз
нет работы силы трения, механическая энергия
системы не меняется.
31.
Рассмотрим энергию цилиндра в начальный момент — навысоте H и в конце спуска. Полная энергия цилиндра в этих
положениях одинакова:
Так как
1
1
2
2
mgh mVC I C
2
2
1
VC
2
I C mR , а
, получаем:
2
2
R
2
1
1 mR VC 3
2
2
mgh mVC
mVC
2
2
2 2 R
4
Отсюда легко найдем конечную скорость цилиндра
.
gh
VC 2
3
32.
Если стоит задача нахождения времени скатывания цилиндра,то для решения нужно воспользоваться уравнением моментов
Из условия «движение без проскальзывания» имеем
связь между угловой скорость и скоростью центра
масс:
V
c
R
Продифференцировав это уравнение по времени,
получим соотношение для ускорений:
ac
V c
или
R
R
Воспользовавшись теоремой о движении центра
масс, опишем поступательное движение
внешн
цилиндра:
F
mg N Fтр maC
33.
Спроецировав уравнение на направления осей x и y,получим два скалярных уравнения:
x:
y:
mgSin – Fтр = maC (1)
N – mgсos = 0
(2)
Для описания вращения воспользуемся основным
уравнением динамики вращательного движения:
1
MC = IC
( I C mR 2 )
2
Из трёх названных сил момент относительно оси
цилиндра создаёт только сила трения:
M C M Fтр Fтр R
34.
Учитывая всё это, уравнение моментов перепишемтак:
1
1
1
2
2 aC
Fтр R mR mR
mR aC (3)
2
2
R 2
Решая совместно уравнения движения(1), (2), и (3)
получим следующие значения неизвестных величин:
1
Fтр mg Sin
3
2
a g Sin
3
Из выражения для Fтр следует, что с увеличением
угла наклона должна возрастать и сила трения
покоя Fтр.
35.
Но, как известно, её рост ограничен предельнымзначением:
Fтр ск N mg Cos
Следовательно, должно выполняться неравенство:
⅓mgSin ≤ mgCos .
Отсюда следует, что скатывание будет
происходить без проскальзывания до тех пор, пока
угол не превзойдёт значения пред:
пред = arctg3 .
Здесь — коэффициент трения цилиндра по
плоскости.
36.
Линейное ускорение цилиндра величина неизменная,следовательно, поступательное движение цилиндра
равноускоренное. При таком движении без начальной
скорости цилиндр достигнет основания наклонной
плоскости за время:
длина наклонной
h
2l , где l
плоскости
t
a
Sin
2
Так как a g Sin , то время скатывания:
3
2 h 3
1
3h
t
Sin 2 g Sin Sin g
37.
Вычислим конечную скорость поступательногодвижения оси цилиндра:
2
1
VC aCt g Sin
3
Sin
3h
gh
2
g
3
Она совпадает с результатом, полученным выше
более простым путем, исходя из закона сохранения
энергии.
38. Сходство и различие линейных и угловых характеристик движения
Формулыкинематики
и
динамики
вращательного
движения
легко
запоминаются, если сопоставить их с
формулами поступательного движения.
Отмечу, что в приведенной ниже таблице
рассмотрены
случаи
движения
с
постоянными ускорениями:
a const
const
39.
Поступательное движениеdφ
ω
dt
dω
ε
dt
ω ω 0 εt
dS
υ
dt
dυ
a
dt
υ υ0 at
2
at
S υ 0t
2
t
S υ dt
0
Вращательное движение
εt
φ ω 0t
2
2
t
φ ωd t
0
40.
dpF
dt
ma F
p m
m const
A FS
N Fv
m
mgh const
2
2
dL
M
dt
Iε M
L Iω
Iω const
A M
N Mw
Iω
mgh const
2
2

































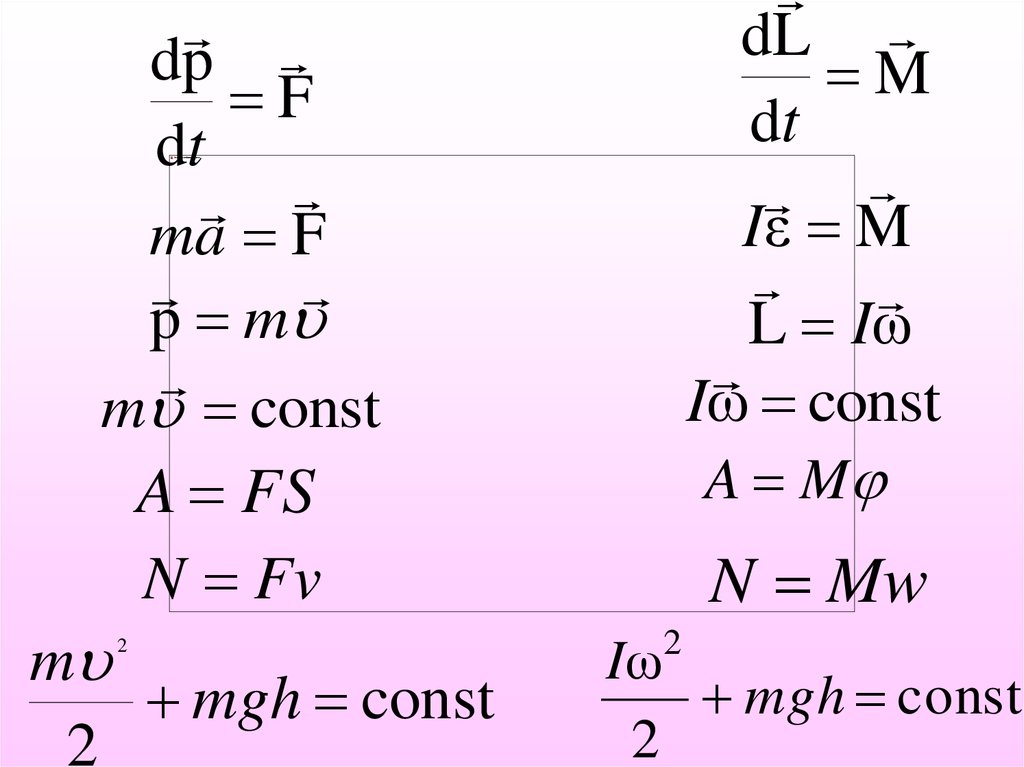


 physics
physics








