Динамика твердого тела

1. Динамика твердого тела

Момент инерции тела.
Момент силы.
Основной закон динамики вращательного
движения.
Момент импульса.
Закон сохранения момента импульса.
Кинетическая энергия вращающегося тела.
Работа силы при вращательном движении.

2. Вращение твердого тела вокруг неподвижной оси

Твердым телом называется тело, которое не
деформируется, т.е. расстояние между двумя
точками этого тела остается постоянным.
Поступательным движением твердого тела
называется такое движение, при котором все
точки тела движутся одинаково ( описывают
одинаковые траектории, имеют одинаковые
перемещения, скорости, ускорения).
Движение твердого тела, при котором две его
точки остаются неподвижными, а остальные
описывают окружности с центрами на прямой,
проходящей через неподвижные точки, называется
вращением вокруг неподвижной оси.

3. Момент инерции

Момент инерции – это мера инертности тела
при вращательном движении.
Момент инерции материальной точки
относительно оси Z
Момент инерции твердого тела
относительно неподвижной оси Z
I z mr
N
N
i 1
i 1
I z I z i mi ri
2
2
I z dI r dm
2
m

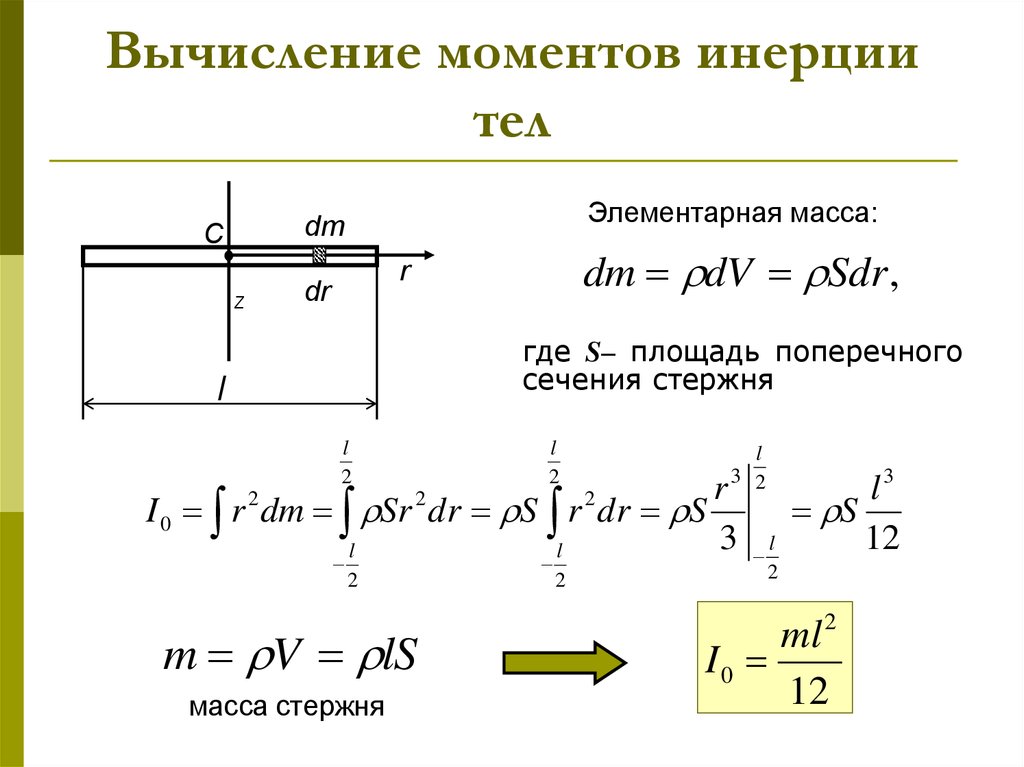
4. Вычисление моментов инерции тел

Элементарная масса:
dm
C
Z
dm dV Sdr ,
r
dr
где S– площадь поперечного
сечения стержня
l
l
2
l
2
l
3 2
r
2
2
2
I 0 r dm Sr d r S r d r S
3
l
l
2
m V lS
масса стержня
2
l
2
l3
S
12
ml 2
I0
12

5. Теорема Штейнера

Момент инерции тела относительно
произвольной оси АА равен сумме момента
инерции этого тела относительно оси СС,
проходящей через центр масс параллельно
рассматриваемой, и произведения массы
тела на квадрат расстояния между осями.
A
C
J AA J CC
l/2
A
C
l
m
2
2

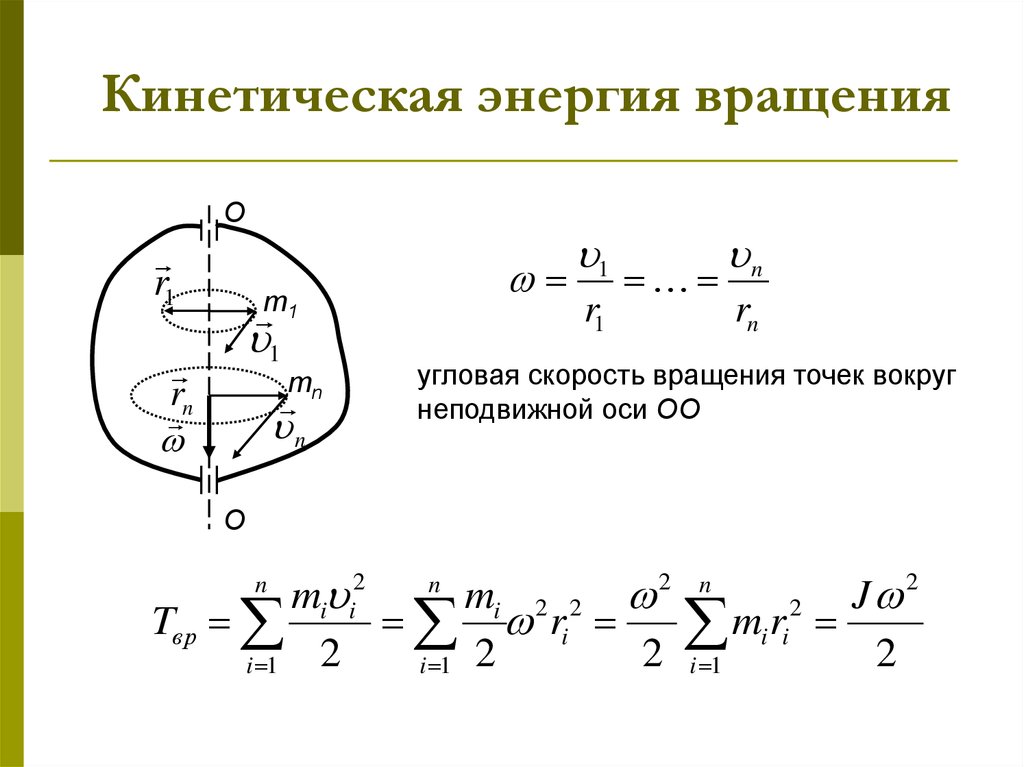
6. Кинетическая энергия вращения

О
r1
m1
1
rn
mn
n
1
r1
n
rn
угловая скорость вращения точек вокруг
неподвижной оси ОО
О
2
n
mi i2
mi 2 2 2 n
J
2
Tвр
ri
m
r
i i
2
2 i 1
2
i 1
i 1 2
n

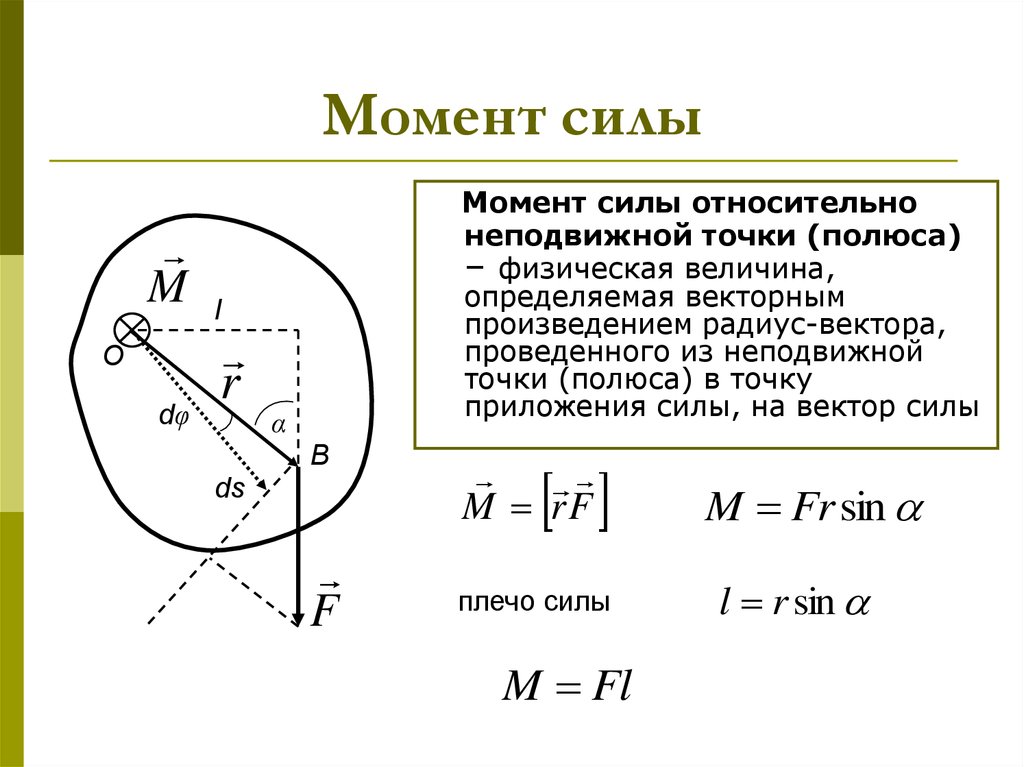
7. Момент силы

M
О
dφ
Момент силы относительно
неподвижной точки (полюса)
– физическая величина,
определяемая векторным
произведением радиус-вектора,
проведенного из неподвижной
точки (полюса) в точку
приложения силы, на вектор силы
l
r
α
В
ds
F
M rF
плечо силы
M Fl
M Fr sin
l r sin

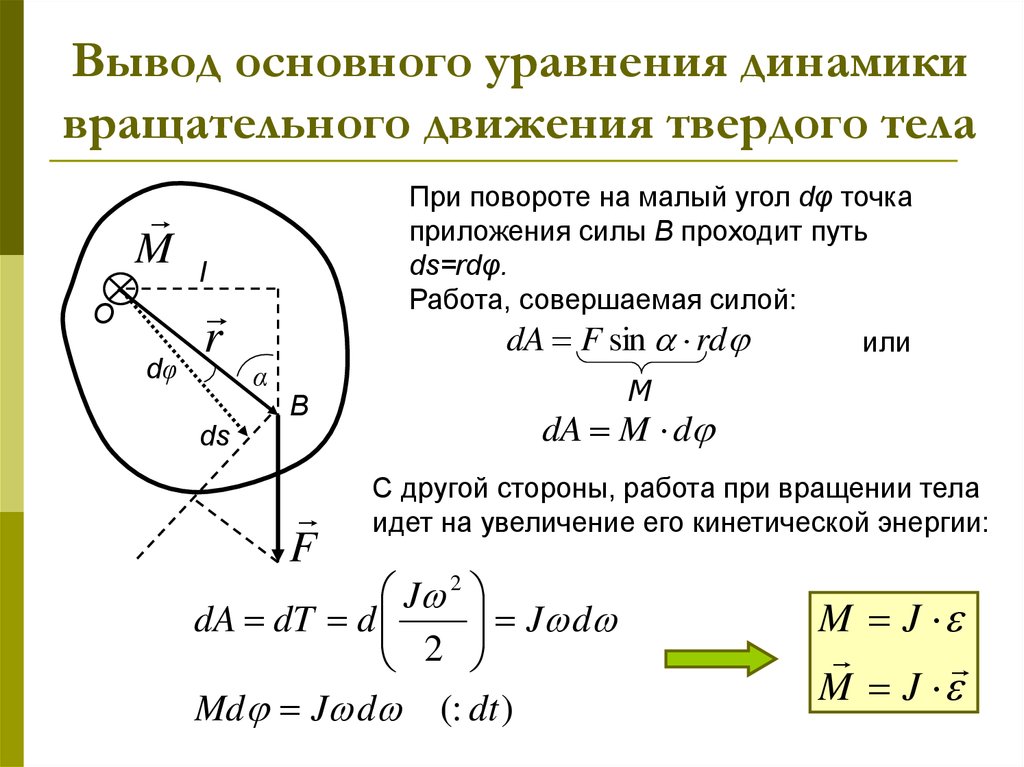
8. Вывод основного уравнения динамики вращательного движения твердого тела

M
О
dφ
При повороте на малый угол dφ точка
приложения силы В проходит путь
ds=rdφ.
Работа, совершаемая силой:
dA F sin rd
или
l
r
α
В
ds
F
М
dA M d
С другой стороны, работа при вращении тела
идет на увеличение его кинетической энергии:
J 2
J d
dA dT d
2
Md J d (: dt )
M J
M J

9. Момент импульса

Момент импульса точки относительно неподвижной
точки (полюса) – физическая величина, определяемая
векторным
произведением
радиус-вектора,
проведенного из неподвижной точки (полюса) в данную
точку, на вектор импульса точки
L r p
L m r sin pl
Момент импульса твердого тела относительно оси:
n
n
n
L mi i ri mi ri mi ri J
2
i 1
i 1
2
i 1

10. Уравнение динамики вращательного движения твердого тела

M J
dL
M
dt
Момент силы, действующей на
тело, равен произведению
момента инерции тела на угловое
ускорение
Скорость изменения момента
импульса
твердого
тела
относительно неподвижной оси
вращения равна моменту всех
внешних сил, действующих на
тело относительно данной оси

11. Закон сохранения момента импульса

Момент импульса твердого тела относительно
неподвижной
оси
остается
величиной
постоянной, если момент всех сил, действующих
на тело, равен нулю
Если
M 0
J const
Закон сохранения момента импульса – фундаментальный
закон природы. Он связан со свойством симметрии
пространства – его изотропностью, т.е. инвариантностью
фундаментальных
законов
природы
относительно
поворота системы в пространстве на любой угол

12.

Поступательное
движение
Вращательное движение
вокруг неподвижной оси
Масса m
Момент инерции J
Перемещение dr
Угловое перемещение d
Скорость
Угловая скорость
Ускорение
Сила
Импульс
dp
F
dt
a d dt
d dt
Угловое ускорение d
dt
p m
Момент импульса
dr dt
F
ma F
Момент силы M
dL
M
dt
L J
J M