Similar presentations:
Механика твердого тела
1. Механика твердого тела
2. Момент инерции
Моментом инерции системы (тела) относительнооси вращения- называется физическая величина,
равная сумме произведений масс n материальных точек системы на квадраты расстояний до
рассматриваемой оси вращения.
J
n
2
m
r
ii
i 1
В случае непрерывного распределения масс:
J r dm
Где интегрирование происходит по всему объему
тела
2
3.
Найдем момент инерции сплошного цилин- hдра высотой h и радиусом R относительно его
R
геометрической оси. Разобьём цилиндр на отdr
дельные полые концентрические цилиндры с
r
внутренним радиусом r и внешним r + dr. Момент инерции каждого концентрического цилиндра
dJ = r2dm (так как считаем, что расстояния от оси до всех
точек на цилиндре r , dr<<r). Где dm масса всего элементарного цилиндра. А его объём dV = 2πr∙h∙dr . Если ρ
плотность материала, то dm = ρ∙2πr∙h∙dr и dJ=ρ∙2πr3∙h∙dr.
Тогда момент инерции сплошного цилиндра:
R
1
J dJ 2 h r dr 2 h R 4
4
0
3
4.
Так как:V R 2 h - объём цилиндра
m V R 2 h- масса цилиндра
Момент инерции:
1
2
J mR
2
5. Теорема Штейнера
Если известен момент инерции тела относительно осипроходящей через его центр масс , то момент инерции относительно любой другой параллельной оси
определяется с помощью теоремы Штейнера .
Момент инерции тела J относительно люa
бой оси вращения, равен моменту его
J
инерции J c относительно параллельной
оси проходящей через центр масс С тела сложенному с произведением массы
тела m на квадрат расстояния a между
осями.
J J c ma 2
Jc
m
C
6. Значение моментов инерций для некоторых однородных тел массой m.
• Полый тонкостенный цилиндр радиусом RR
J mR 2
• Сплошной тонкостенный цилиндр радиусом R
R
1
J mR 2
2
• Шар радиусом R (ось проходит через центр )
R
2
J mR 2
5
• Прямой тонкий стержень длинной L (ось
перпендикулярна стержню, проходит через его
1
J
ml 2
середину
12
L
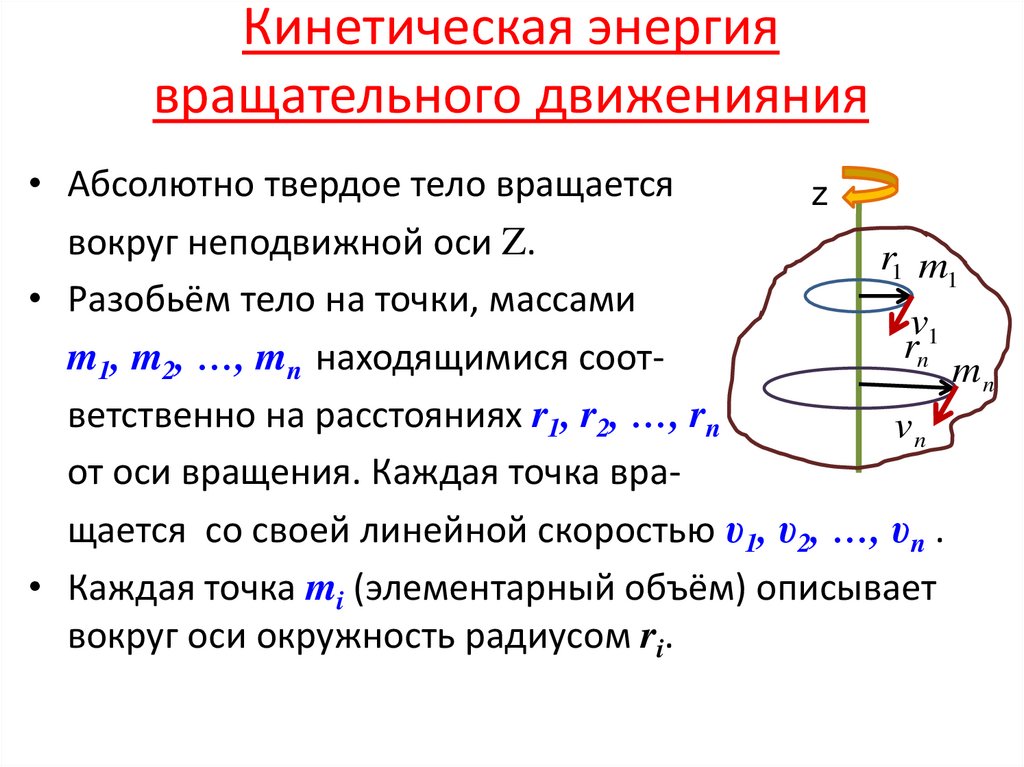
7. Кинетическая энергия вращательного движенияния
• Абсолютно твердое тело вращаетсяz
вокруг неподвижной оси Z.
r1 m1
• Разобьём тело на точки, массами
v1
rn
m1, m2, …, mn находящимися соотmn
ветственно на расстояниях r1, r2, …, rn
vn
от оси вращения. Каждая точка вращается со своей линейной скоростью υ1, υ2, …, υn .
• Каждая точка mi (элементарный объём) описывает
вокруг оси окружность радиусом ri.
8.
• Так как мы рассматриваем абсолютно твердое тело, тоугловая скорость вращения всех элементарных
объёмов будет одинакова
vn
v1 v2
...
r1
r2
rn
• Кинетическую энергию вращающегося тела, найдем
как сумму кинетических энергий элементарных объn
mn vn2
mi vi2
m1v12 m2 v22
ёмов:
Еквр
2
2
...
2
vi
• Так как i
то
ri
n
n
mi vi2
mi i2 ri 2 2
Еквр
2
2
2
i 1
i 1
i 1
n
2
2
m
r
ii
i 1
2
2
Jz
где J z - момент инерции тела относительно оси z
9.
Е кв р2
2
Jz
Формула справедлива для тела вращающегося вокруг
оси. Если, кроме вращательного, тело совершает и
поступательное движение, то энергия движения
складывается из кинетических энергий поступательного и вращательного движений.
Å ê Å êï Å êâð
m c2 J c 2
2
2
где: m - масса тела
c - скорость центра масс тела
J c - момент инерции тела относительно оси проходящей через центр масс.
10. Момент силы. Уравнение динамики вращательного движения твердого тела
11.
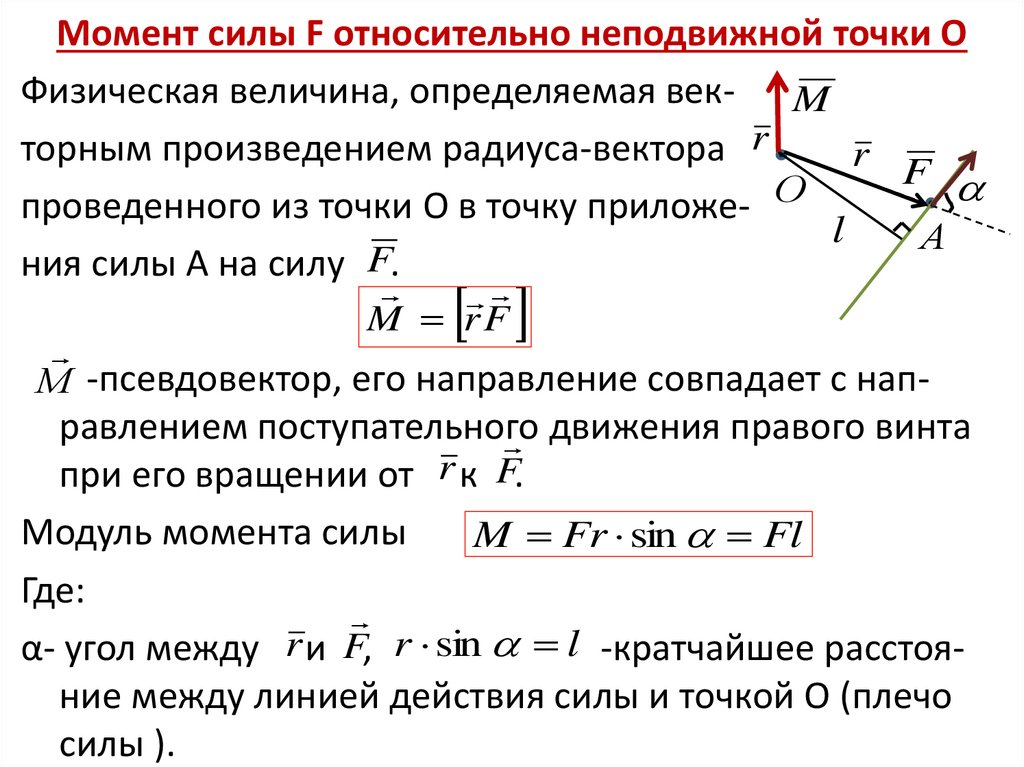
Момент силы F относительно неподвижной точки ОФизическая величина, определяемая век- M
торным произведением радиуса-вектора r
r F
проведенного из точки О в точку приложе- О
l
А
ния силы А на силу F.
M rF
М -псевдовектор, его направление совпадает с нап-
равлением поступательного
движения правого винта
при его вращении от r к F.
Модуль момента силы
M Fr sin Fl
Где:
α- угол между r и F, r sin l -кратчайшее расстояние между линией действия силы и точкой О (плечо
силы ).
12.
• Момент сил относительно неподвижной осиz
-скалярная величина M z , равная проек
Mz F
ции на ось Z вектора M момента силы,
определённого относительно произволь- M
А
r
О
ной точки О данной оси.
Если ось Z совпадает с направлением вектора M , то
момент силы представляется в виде совпадающего с
осью вектора
M z rF
z
13.
•При вращении тела работа определяется следующимобразом:
В
dS
Пусть сила F приложена в точке В находяd
щейся от оси вращения на расстоянии r,
r
О
F
α-угол между направлением силы и радиус
вектором r . Так как тело абсолютно твёрдое, то работа
этой силы равна работе, затраченной на поворот всего
тела.
При повороте тела на бесконечно малый угол d ,
точка приложения В проходит путь dS rd , и работа
равна произведению проекции силы на направление
смещения на величину смещения.
dA F sin r d M z d
14.
Fr sin M zM z -момент силы относительно оси Z . Работа при
вращении тела равна произведению момента
действующей силы на угол поворота.
Работа при вращении тела идёт на увеличение его
кинетической энергии dA dE k
J z 2
dE k d
2
J z d M z d J z d
d
d
Mz
J z
dt
dt
d
d
d d
d
Mz
Jz
Mz Jz
J z
dt
dt
dt dt
dt
15.
Уравнение динамики вращательного движениятвердого тела относительно неподвижной оси
M z J z
16. Момент импульса и закон его сохранения
17.
• Момент импульса (количество движения) материальной точки А относительно неподвижной точки ОФизическая величина, определяемая век- L
p
торным произведением:
r
О
L r p r mv
l
А
Где:
• r -радиус-вектор проведенный из точки О в точку А
• p mv - импульс материальной точки
• L -псевдовектор, его направление совпадает с направлением поступательного движения
правого винта
при его движении от к . r p
Модуль вектора момента импульса:
L rp sin mvr sin pl
18.
• Момент импульса относительно неподвижной оси Zскалярная величина L z равная проекции на эту осьвектора момента импульса относительно точки О
данной оси. Значение L z не зависит от положения
точки О на оси Z.
• При вращении абсолютно твердого тела, каждая отдельная
по окружности радиу точка тела движется
r
сом i со скоростью v i . Момент импульса отдельной
точки Lz mi vi ri . Скорость и импульс перпендикулярны радиусу,
то есть радиус является плечём век
тора mi vi . Момент импульса направлен в сторону
определяемую правилом правого винта.
19.
• Момент импульса тела-сумма моментов импульсовотдельных частиц.
Lz J z
n
n
n
L z mi vi ri mi ri mi ri 2 J z
2
i 1
i 1
i 1
• Продифференцируем данное выражение:
dLz
d
Jz
J z M z
dt
dt
• Уравнение динамики вращательного движения
твердого тела относительно неподвижной осипроизводная момента импульса относительно оси
равна моменту сил относительно той же оси.
dL
dLz
Mz
M
dt
dt
20.
Закон сохранения момента импульса:Момент импульса замкнутой системы сохраняется,
то есть не изменяется с течением времени.
(фундаментальный закон природы)
L const
В замкнутой системе момент внешних сил
dL
M 0
0 L const
dt
21. Элементы механики жидкостей
22.
• В механике жидкости и газы рассматриваются каксплошные, непрерывно распределяемые в занимаемой ими части пространства вещества. Поэтому,
при решении многих задач, используют понятие несжимаемой жидкости -жидкости, плотность которой
всюду одинакова, и не изменяется со временем.
• Давление –физическая величина, определяемая
нормальной силой, действующей со стороны жидкости на единицу площади.
F
p
S
Единица давления-Паскаль (Па) 1Па=1 Н/м²
• Давление при равновесии жидкостей подчиняется
закону Паскаля.
23. Закон Паскаля
Давление в любом месте покоящейся жидкости одинакого по всем направлениям, причем, давление передается одинаково по всему объёму занятому покоящейсяжидкостью.
При равновесии жидкости давление по горизонтам везде одинаково, иначе не было бы равновесия. Значит,
свободная поверхность покоящейся жидкости всегда
горизонтальна (вдали от стенок сосуда). Если жидкость
несжимаемая , то её плотность не зависит от давления.
Тогда, при поперечном сечении S столба жидкости, его
высоте h и его плотности ρ вес столба жидкости и давление на нижнее основание столба
P ghS
P
ghS
p
gh
S
S
24.
p ghДанное давление назывется: гидростатическим.
Гидростатическое давление линейно изменяh
ется с высотой, и давление на нижние слои
жидкости будет больше чем на верхние, поэтому на тело погруженное в жидкость действует выталкивающая сила определяемая ЗАКОНОМ
АРХИМЕДА.
S
ρ
g
25. Закон Архимеда
На тело погруженное в жидкость (газ) действуетсо стороны этой жидкости направленная вверх
выталкивающая сила, равная весу вытесненной
телом жидкости (газа).
FA gV
где:
ρ´-плотность жидкости
V –объём погруженного в жидкость тела
26. Уравнение неразрывности. Уравнение Бернулли.
27.
Движение жидкостей называется течением , совокупность частиц движущейся жидкости потоком .Пусть поток проходит через сечения
S1 v1
S2 v
2
S1 и S2 различного размера, перпендикулярных направлению скорости.
За время Δt через сечение S1 пройдет объём жидкости
V=S1v1Δt, значит за 1 секунду через S1 пройдет
объём жидкости S1v1 где v1-скорость течения
жидкости в месте сечения S1. Через сечение S2 за
1 секунду аналогично пройдет объём S2v2. Скорость течения жидкости в сечении постоянна.
Если жидкость несжимаемая, то через сечение S2
пройдет тот же объём жидкости что и через S1.
28.
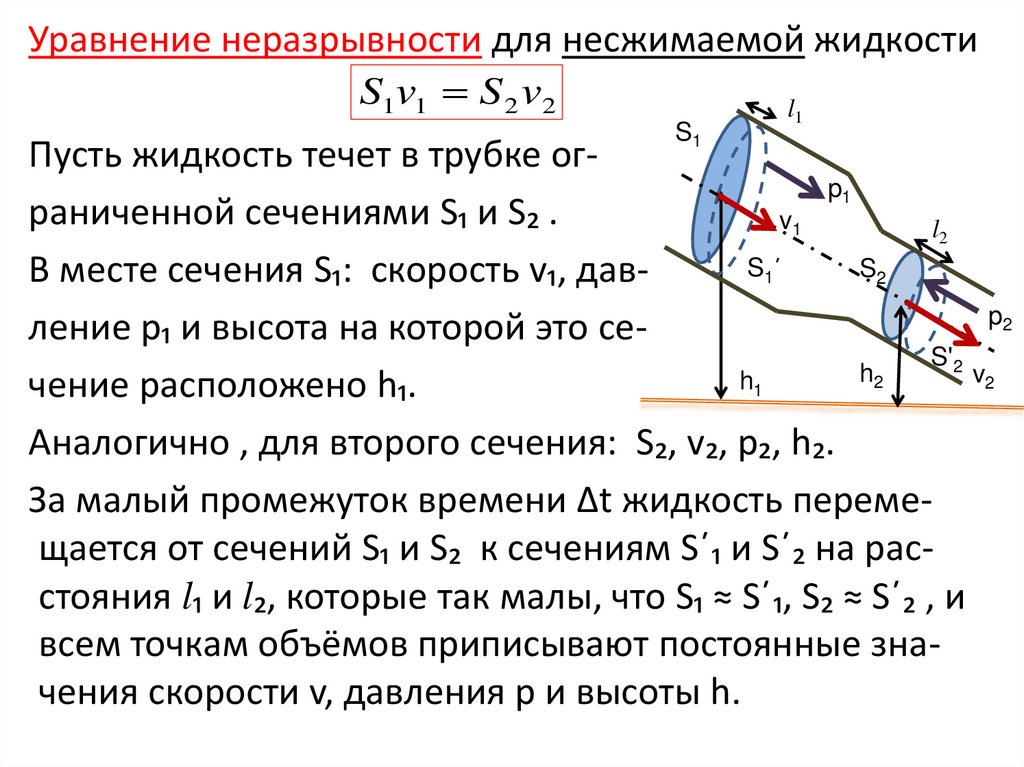
Уравнение неразрывности для несжимаемой жидкостиS1v1 S 2 v2
l1
S1
Пусть жидкость течет в трубке огp1
раниченной сечениями S₁ и S₂ .
v1
l2
S1´
S2
В месте сечения S₁: скорость v₁, давp2
ление p₁ и высота на которой это сеS'2
h
v2
2
h1
чение расположено h₁.
Аналогично , для второго сечения: S₂, v₂, p₂, h₂.
За малый промежуток времени Δt жидкость перемещается от сечений S₁ и S₂ к сечениям S´₁ и S´₂ на расстояния l₁ и l₂, которые так малы, что S₁ ≈ S´₁, S₂ ≈ S´₂ , и
всем точкам объёмов приписывают постоянные значения скорости v, давления p и высоты h.
29.
Согласно закону сохранения энергии, изменение полной энергии несжимаемой жидкости должно бытьравно работе А внешних сил по перемещению массы m жидкости.
A E2 E1
Где:
•E2 , E1 -полные энергии жидкости массой m в местах
сечений S₁ и S₂.
• A -работа совершаемая при перемещении всей
жидкости, заключенной между сечениями S₁ и S₂ за
рассматриваемый малый промежуток времени Δt .
Для перемещения массы m от S₁ до S´₁ жидкость
должна переместиться на расстояние l1 v1 t ,
l 2 v2 t следовательно:
30.
A F1l1 F2 l 2Где: F1 p1 S1
F2 p2 S 2 (отрицательна так как направлена
в сторону противоположную течению жидкости)
Полные энергии E2 , E1 будут складываться из кинетической и потенциальной энергий массы m жидкости:
2
1
mv
E1
mgh1
2
Так как
mv22
E2
mgh2
2
E2 E1 p1 S1l1 p2 S 2 l 2
То можно представить:
31.
mv12mv22
mgh1 p1 S1v1 t
mgh2 p 2 S 2 v 2 t
2
2
Согласно уравнению неразрывности для несжижаемой жидкости, объём занимаемый жидкостью
постоянен
V S1v1 t S 2 v2 t
m
Так как
(плотность жидкости) разделив обе
V
части уравнения
на Vполучим:
v12
2
gh1 p1
v 22
2
gh2 p 2
Так как площадь сечений выбирались произвольно
то:
32.
Уравнение Бернуллиv 2
gh p const
2
Уравнение Бернулли-выражение закона сохранения
энергии применительно к установившемуся течению идеальной жидкости.
• p -статическое давление (давление жидкости на
поверхность обтекаемого ею тела)
2
v
-динамическое давление
2
• gh - гидростатическое давление
Для горизонтальной трубки h1 h2 :
v 2
-полное давление
p const
2





























 physics
physics








