Similar presentations:
Динамика твердого тела
1. 4. Динамика твердого тела Любое сложное движение твердого тела (т.т.) - результат сложения поступательного и вращательного
движений.В случае поступательного движения достаточно описать движение одной
точки твердого тела – центра масс или центра инерции.
Это точка равновесия, в ней помещают опору. В однородном поле силы
тяжести это точка приложения веса тела, обозначим ее С.
Обозначим радиус – вектор центра масс
, массу тела m ,
силу, действующую на тело и приложенную к центру масс
.
Тогда 2-- й закон Ньютона можно
записать только для одной точки –
центра масс тела:
Для системы материальных точек
радиус – вектор центра масс
системы
2. Динамика вращательного движения твердого тела
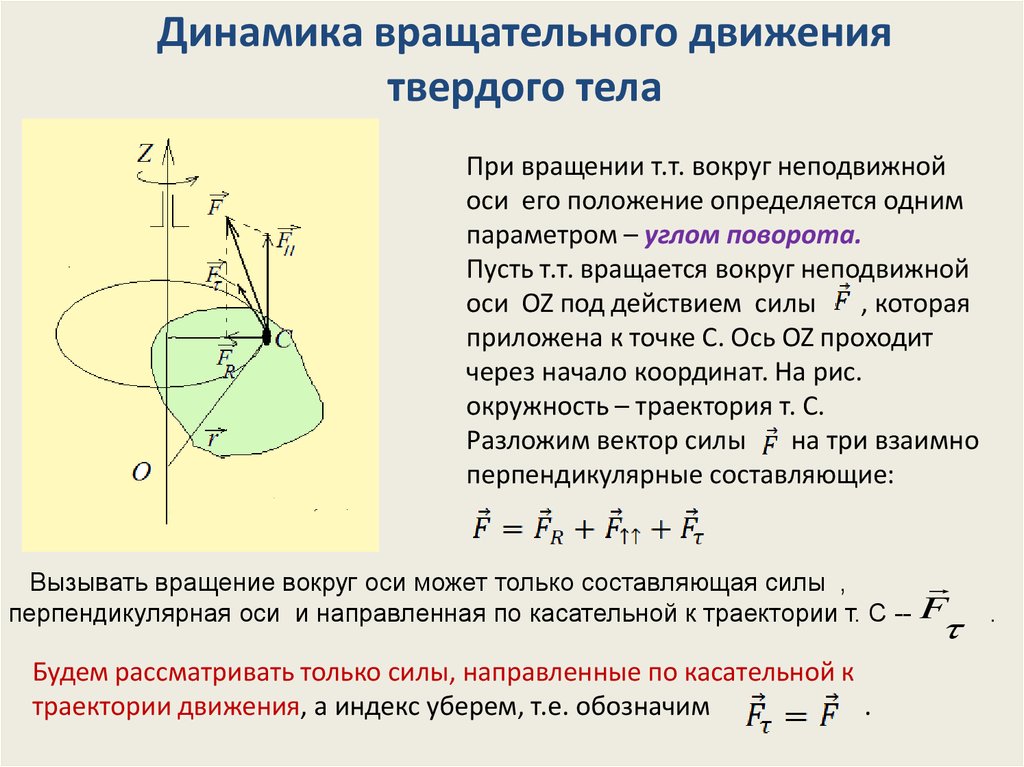
При вращении т.т. вокруг неподвижнойоси его положение определяется одним
параметром – углом поворота.
Пусть т.т. вращается вокруг неподвижной
оси OZ под действием силы
, которая
приложена к точке С. Ось OZ проходит
через начало координат. На рис.
окружность – траектория т. С.
Разложим вектор силы
на три взаимно
перпендикулярные составляющие:
Вызывать вращение вокруг оси может только составляющая силы ,
перпендикулярная оси и направленная по касательной к траектории т. С --
Будем рассматривать только силы, направленные по касательной к
траектории движения, а индекс уберем, т.е. обозначим
.
F
.
3.
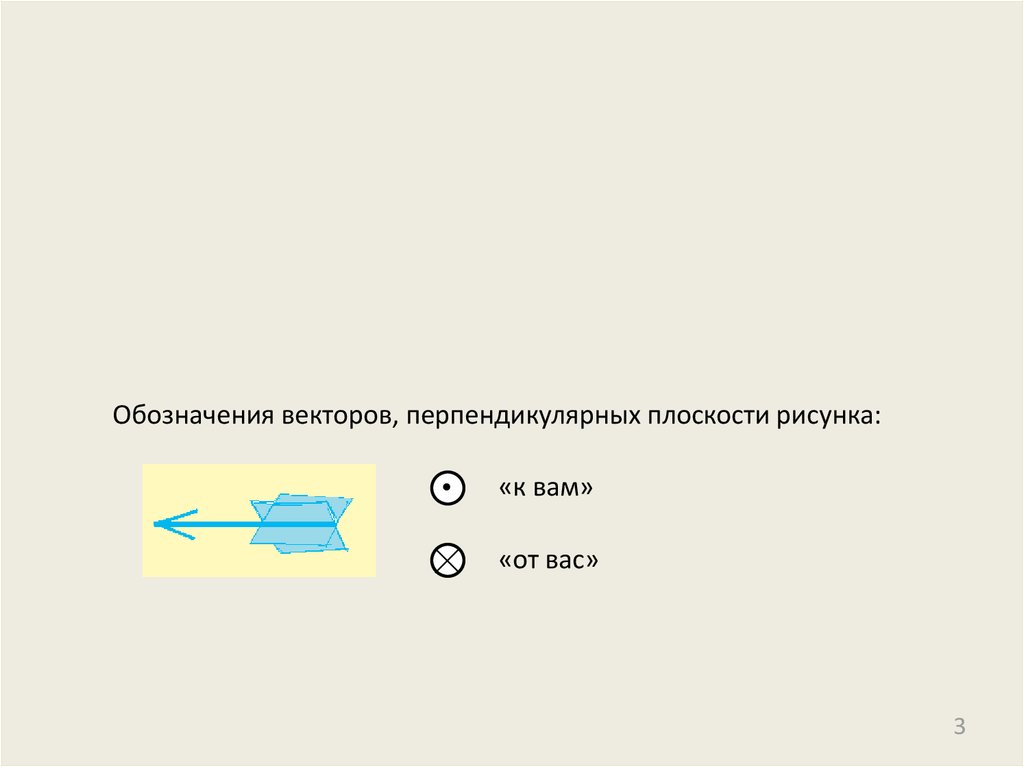
Обозначения векторов, перпендикулярных плоскости рисунка:«к вам»
«от вас»
3
4. 4.1 Момент силы материальной точки относительно точки и оси. Момент импульса материальной точки относительно точки и оси.
Запишем для т. С 2-й закон Ньютона) и умножим его слева векторно на
(под
:
понимается только
(*)
Рассмотрим производную по времени от векторного произведения:
(1)
Т.к. 1-е слагаемое в (1) равно нулю, то выражение (*) запишется так:
Обозначим
Тогда (*) выглядит так:
,
(2)
5. Справка из векторной алгебры:
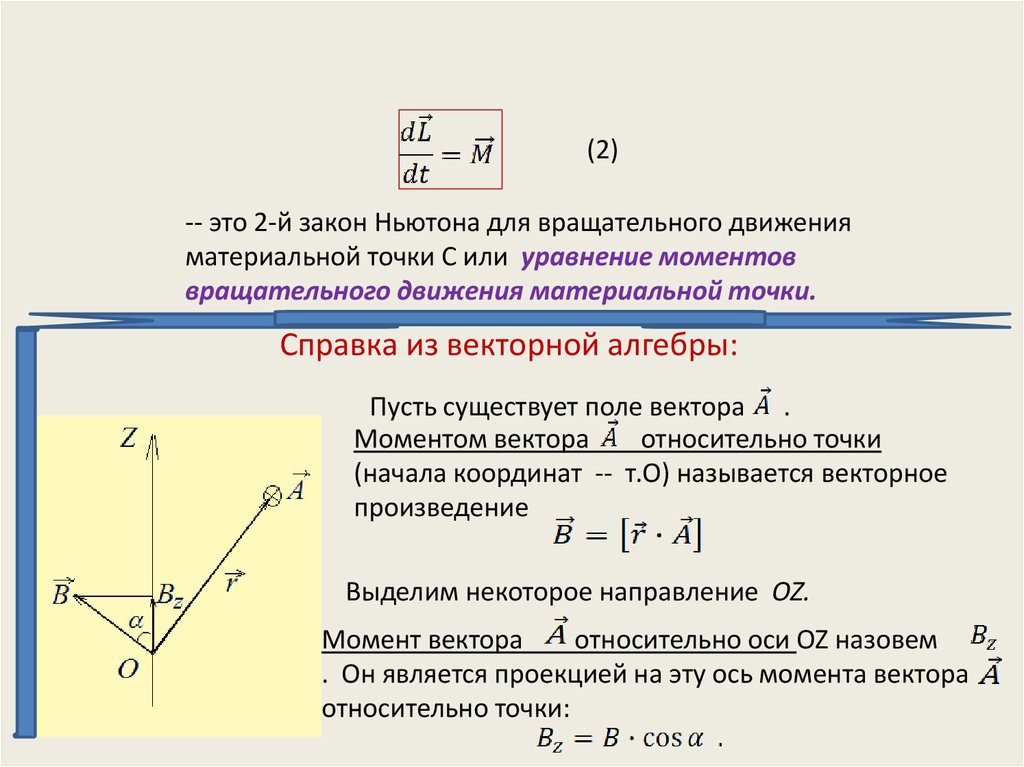
(2)-- это 2-й закон Ньютона для вращательного движения
материальной точки С или уравнение моментов
вращательного движения материальной точки.
Справка из векторной алгебры:
Пусть существует поле вектора .
Моментом вектора
относительно точки
(начала координат -- т.О) называется векторное
произведение
Выделим некоторое направление OZ.
Момент вектора
относительно оси OZ назовем
. Он является проекцией на эту ось момента вектора
относительно точки:
6. Моментом силы материальной точки С относительно точки (начала координат) называется векторное произведение
Направление вектора момента силыM
определяется по правилу правого винта; вектор
M
rи F
направлен перпендикулярно плоскости, в
которой лежат векторы
, и совпадает с направлением поступательного
движения правого винта при его вращении от
r
к
F
кратчайшим путем.
M
В силу условности выбора направления вектора
момент силы является псевдовектором. Его модуль M=rF.
Вектор
┴ плоскости, образованной векторами
Спроецируем
на ось OZ :
и
.
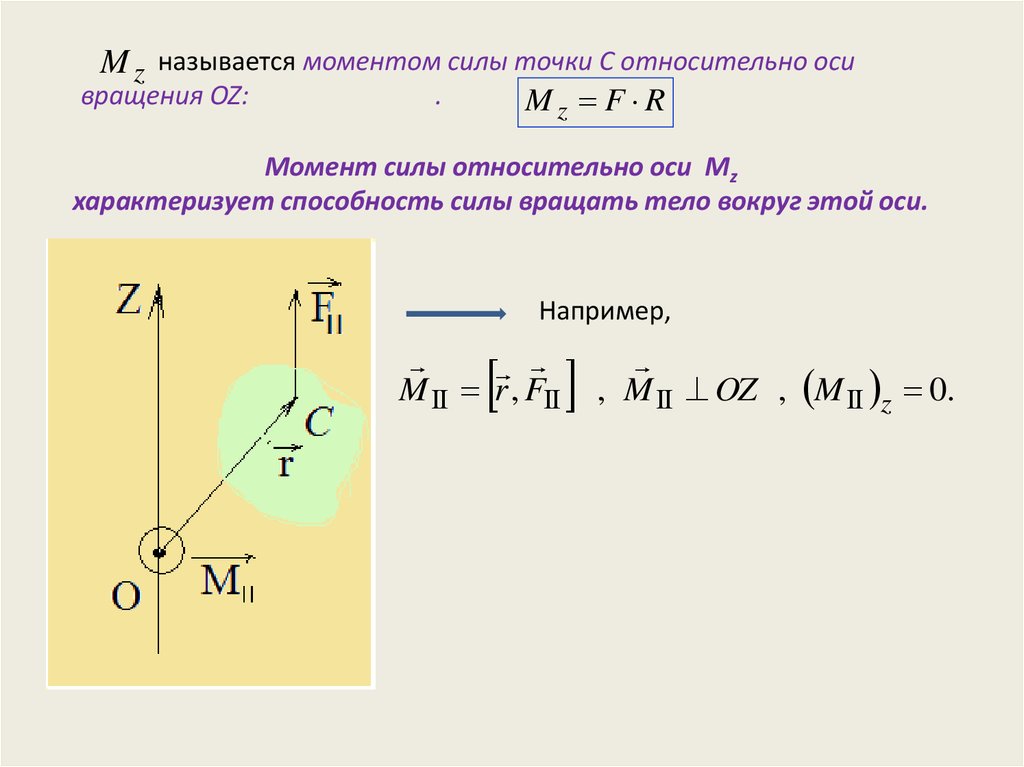
7. Момент силы относительно оси Mz характеризует способность силы вращать тело вокруг этой оси.
M z называется моментом силы точки С относительно осивращения OZ:
Mz F R
.
Момент силы относительно оси Mz
характеризует способность силы вращать тело вокруг этой оси.
Например,
M r , F
, M OZ , M z 0.
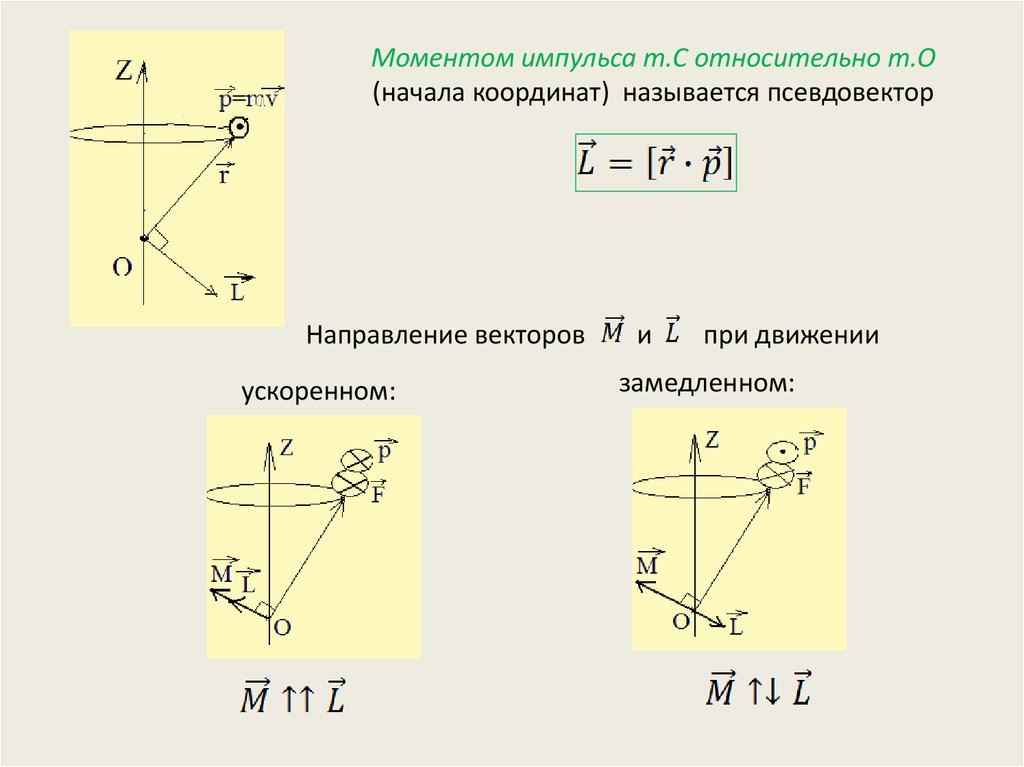
8. Моментом импульса т.С относительно т.О (начала координат) называется псевдовектор
Направление векторовускоренном:
и
при движении
замедленном:
9. Спроецируем момент импульса на ось вращения:
(**)Эта величина ( ) называется моментом
импульса м.т. С относительно оси вращения.
Модуль момента импульса точки, вращающейся по окружности,
относительно центра окружности:
L m R.
Моменты сил и моменты импульсов обладают свойством аддитивности,
т.е. их можно складывать. Например, для системы, состоящей из N
материальных точек
момент импульса системы:
момент силы , действующий на систему:
10. 4.2 Основное уравнение вращательного движения твердого тела (2-й закон Ньютона для вращательного движения т.т.)
Пусть твердое тело вращается вокруг некоторой оси, закрепленнойнеподвижно относительно выбранной системы отсчета.
В этом случае все точки твердого тела вращаются по окружностям,
центры которых лежат на оси ОZ. Т.т. можно рассматривать как систему
частиц (или м.т.) с неизменными расстояниями между ними.
Пусть тело состоит из n частиц; запишем для i – й частицы уравнение
моментов (2) :
Сложим почленно все уравнения
моментов, записанные для всех м.т.
системы (т.е. для всего тела) :
.
(3)
11. Посмотрим на тело сверху. Пусть начало координат, м.т. и лежат в плоскости рис. Внутренние для данного тела силы взаимодействия
частиц действуют вдоль одной прямой .12. Моменты внутренних сил попарно уравновешивают друг друга и выражение (3) можно записать так:
(4)Момент импульса тела относительно точки:
Результирующий момент внешних сил, действующих на тело:
Запись (4) упрощается:
(5)
Это основное уравнение вращательного движения твердого тела
в общем виде:
скорость изменения момента импульса тела относительно начала
координат равна моменту внешних сил, действующих на тело.
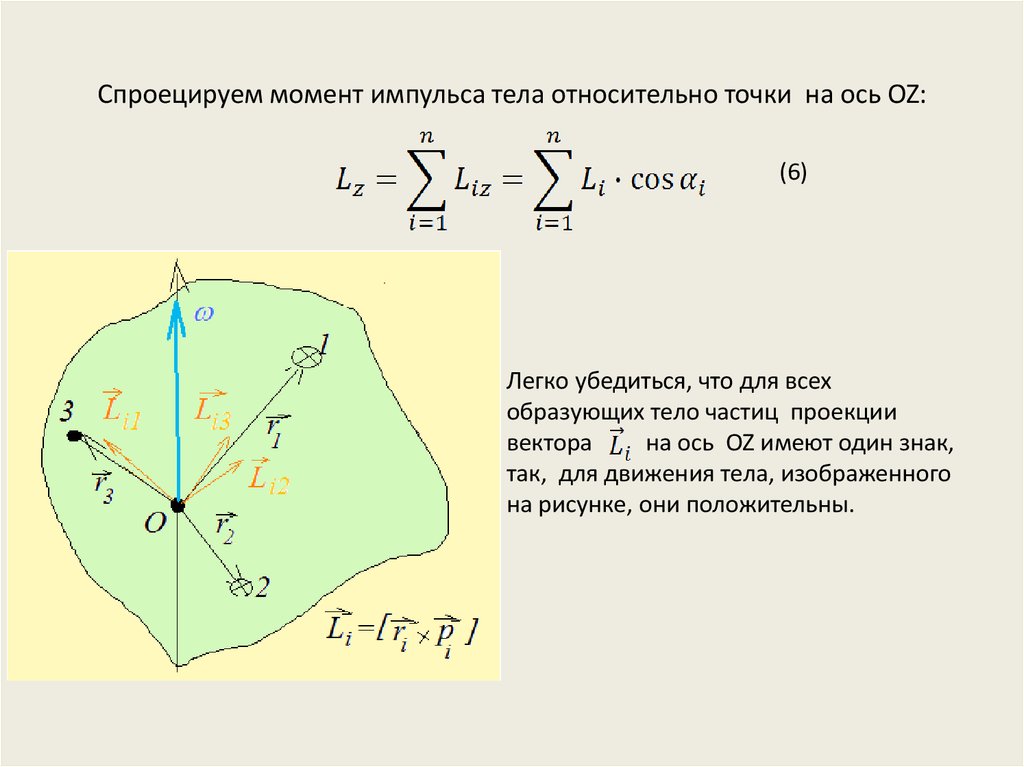
13. Спроецируем момент импульса тела относительно точки на ось OZ:
(6)Легко убедиться, что для всех
образующих тело частиц проекции
вектора
на ось OZ имеют один знак,
так, для движения тела, изображенного
на рисунке, они положительны.
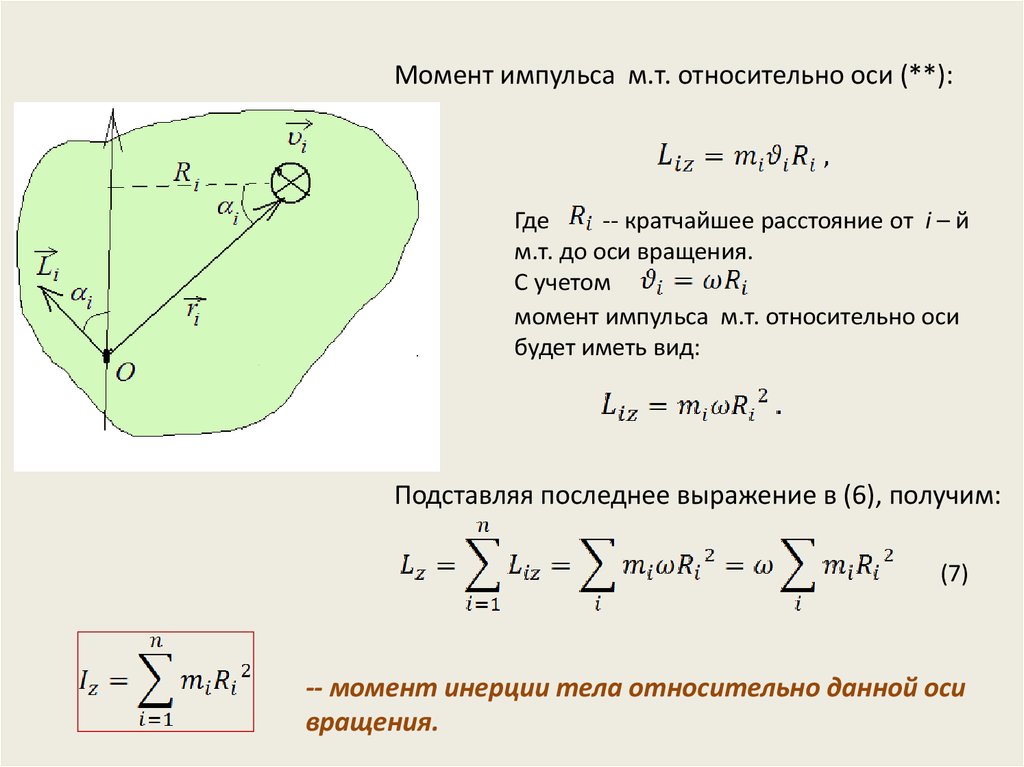
14. Момент импульса м.т. относительно оси (**):
Где-- кратчайшее расстояние от i – й
м.т. до оси вращения.
С учетом
момент импульса м.т. относительно оси
будет иметь вид:
Подставляя последнее выражение в (6), получим:
(7)
-- момент инерции тела относительно данной оси
вращения.
15. Момент инерции тела относительно данной оси вращения равен сумме произведений элементарных масс на квадрат их кратчайшего
расстояния до этой оси .Тогда (7) можно записать так:
(8)
Момент импульса тела относительно оси вращения равен
произведению момента инерции тела относительно этой оси на его
угловую скорость.
В общем случае направления векторов L и не совпадают. Положение
упрощается для однородных тел, симметричных относительно оси вращения.
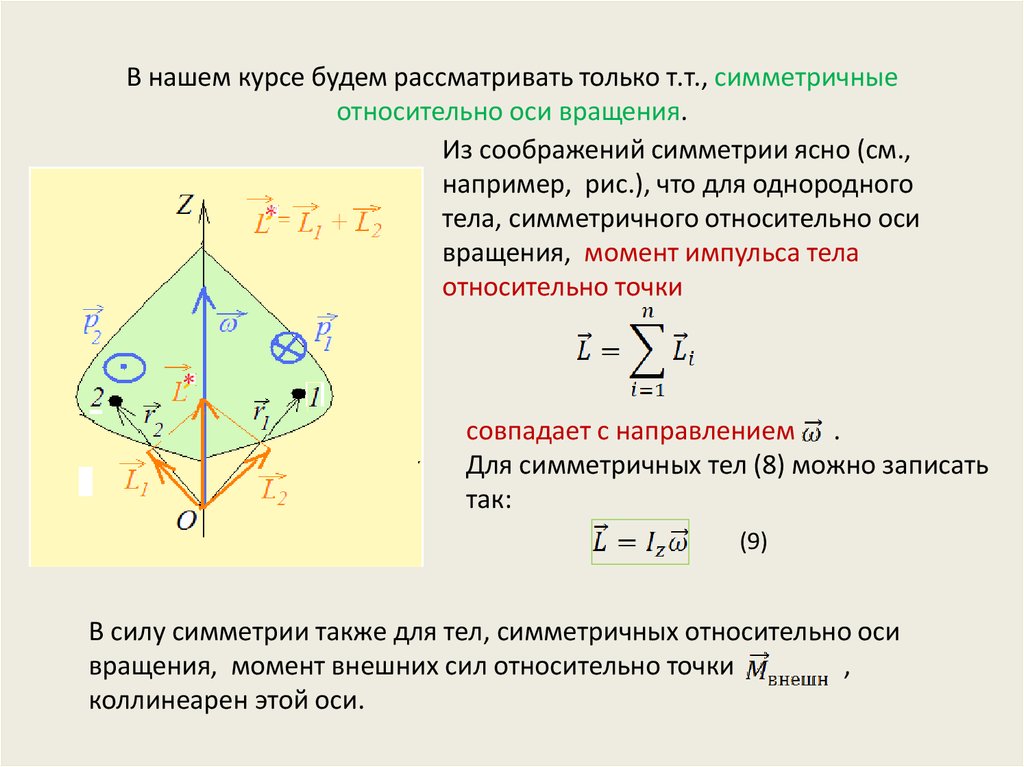
16. В нашем курсе будем рассматривать только т.т., симметричные относительно оси вращения.
Из соображений симметрии ясно (см.,например, рис.), что для однородного
тела, симметричного относительно оси
вращения, момент импульса тела
относительно точки
совпадает с направлением .
Для симметричных тел (8) можно записать
так:
(9)
В силу симметрии также для тел, симметричных относительно оси
вращения, момент внешних сил относительно точки
,
коллинеарен этой оси.
17. С учетом (9 ) и того, что момент инерции т.т. от времени не зависит, основное уравнение вращательного движения для т.т.,
симметричных относительно оси вращения, имеет вид:или:
В скалярном виде:
Момент силы, вращающий тело вокруг данной оси, равен
произведению момента инерции тела относительно этой оси
вращения на угловое ускорение тела.
По аналогии с записью
2 –го закона Ньютона в поступательном
движении( ma F , где -- мера инертности тела ) можно заключить,
что:
момент инерции тела относительно данной оси – мера его инертности
при вращении относительно этой оси.
18.
момент инерции тела относительно данной оси – мера его инертности привращении относительно этой оси.
Пример 1: пластилиновые фигуры.
Пример 2: карусель.
19. 4.3 Закон сохранения момента импульса. Запишем основное уравнение вращательного движения для тела или системы тел:
Если система изолирована или моменты внешних сил скомпенсированы,то
,
следовательно
.
Или:
Если сумма моментов внешних сил, действующих на систему, равна
нулю, то момент импульса системы остается постоянным.
Последнее утверждение называется законом сохранения момента
импульса системы.
20.
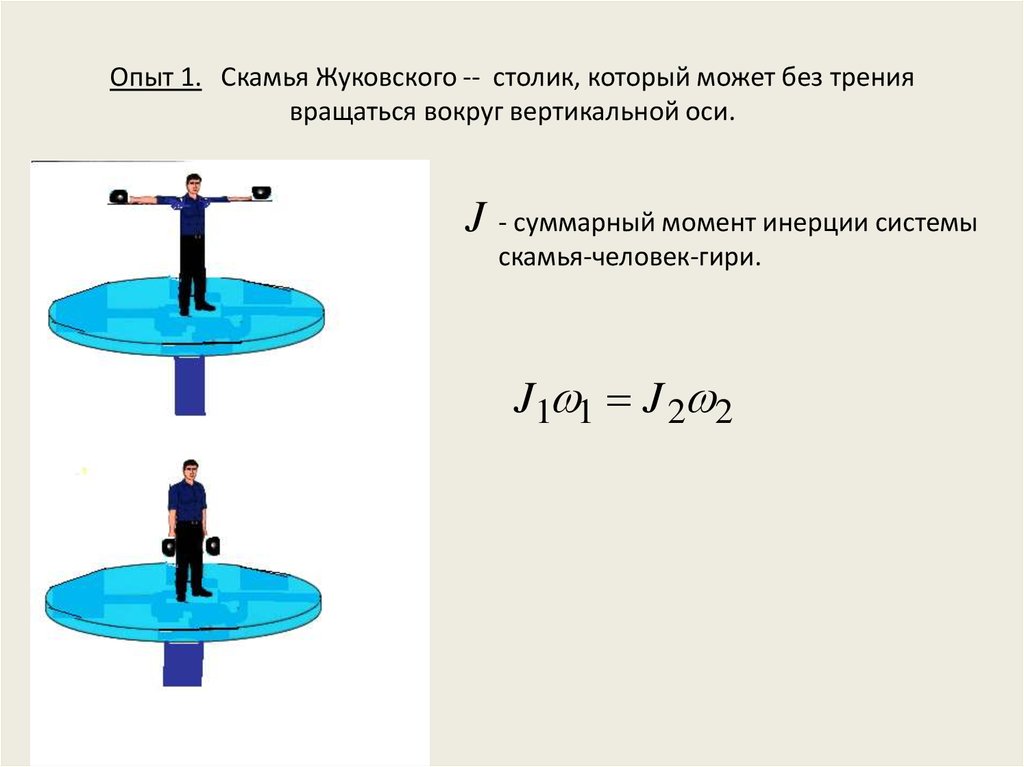
J1 1 J 2 221. Опыт 1. Скамья Жуковского -- столик, который может без трения вращаться вокруг вертикальной оси.
J - суммарный момент инерции системыскамья-человек-гири.
J1 1 J 2 2
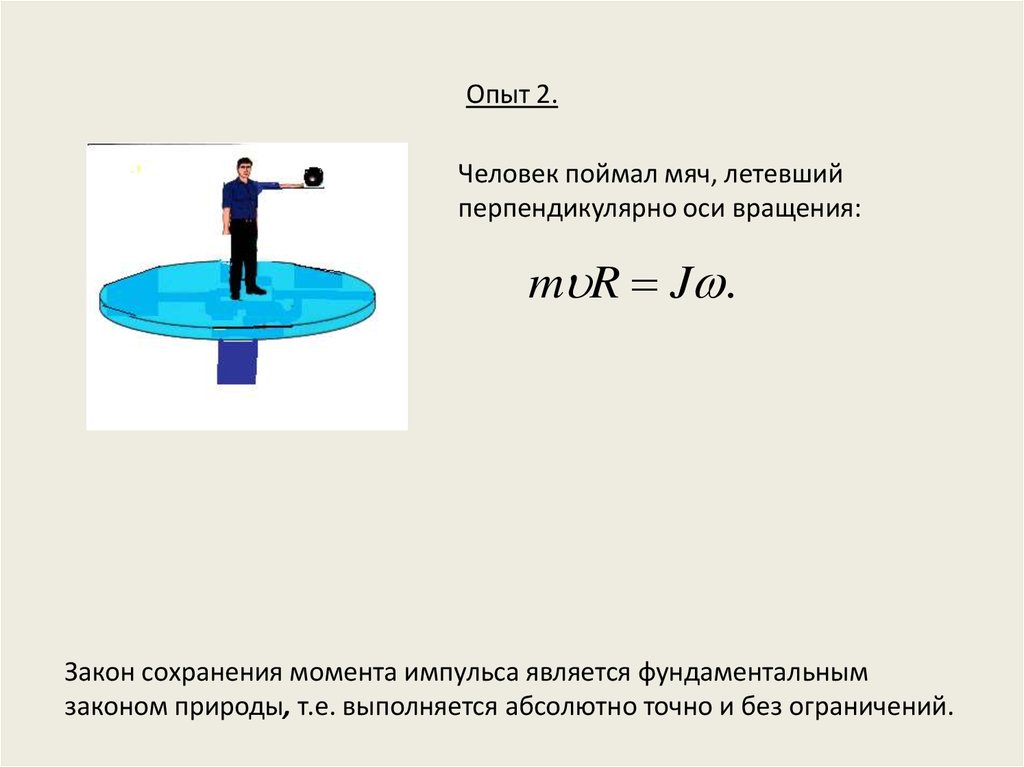
22. Опыт 2.
Человек поймал мяч, летевшийперпендикулярно оси вращения:
m R J .
Закон сохранения момента импульса является фундаментальным
законом природы, т.е. выполняется абсолютно точно и без ограничений.
23.
ОПЫТ 3Человек сидит на неподвижной скамье, ось колеса расположена вертикально.
Колесо приобретает импульс,
вектор момента импульса направлен при этом вверх. Так как система замкнутая, то
человек со скамьей
начинает вращаться в противоположном направлении, при этом вектор момента
импульса направлен по оси
вращения вниз.
Следует обратить внимание на то, что угловая скорость вращения скамьи
значительно меньше, чем угловая
скорость колеса. Это объясняется тем, что колесо имеет меньший момент инерции,
чем скамья с человеком
24. 4.4 Момент инерции. Примеры его вычисления.
Итак, момент инерции твердого тела относительно данной оси можнотрактовать как количественную меру инертности тела относительно
этой оси.
Момент инерции тела относительно данной оси существует
независимо от того, вращается ли данное тело или нет.
Момент инерции - аддитивная, скалярная величина.
Если считать, что в объеме твердого тела вещество
распределено непрерывно, для вычисления момента инерции
N
тела необходимо от суммирования : m R 2 J
i i
z
i 1
перейти к интегрированию.
Выразив элементарную массу dm :
dm dV
,
определение момента инерции запишем в виде
J R(m) 2dm R(V ) 2 dV ,
z
V
где суммирование по всем материальным точкам
заменено интегрированием по объему твердого тела.
25. Величина R(V) определяет расстояние от элементарного объема dV до оси, относительно которой вычисляется момент инерции тела.
Для однородного тела const и поэтому вычисление моментаинерции тела упрощается:
J R(V ) dV
z
V
2
Приведем примеры вычисления моментов инерции относительно оси,
проходящей через центр масс, для некоторых однородных тел правильной
геометрической формы.
Пример 1. Момент инерции тонкого однородного стержня массой m и длиной
, имеющего сечение S произвольной формы, относительно оси, проходящей
через его середину перпендикулярно стержню.
Т.к.
26. Пример 2. Момент инерции однородного сплошного диска массой m, толщиной h и радиусом R относительно его оси симметрии.
.Пример 2. Момент инерции однородного сплошного диска массой m,
толщиной h и радиусом R относительно его оси симметрии.
.
Разобьем диск на концентрические
слои радиуса x и бесконечно малой
толщины dx. Масса такого слоя dm
легко вычисляется:
dm dV 2 xdx h, R x;
подставим
интеграл
эти
выражения
J dm R 2
z
V
и проведем интегрирование:
R
R4
2
J 2 xdx h x 2 h
4
0
Учитывая, что R 2 h m, получим
J
2
mR
2
в
27. Приведем соотношения, определяющие моменты инерции некоторых однородных симметричных тел: - момент инерции материальной точки
Приведем соотношения, определяющие моменты инерции некоторыходнородных симметричных тел:
;
- момент
инерции материальной точки относительно произвольной оси:
,
J mR 2 ;
- момент инерции тонкого стержня относительно оси, проходящей через его
середину перпендикулярно стержню:
m 2
J
12
- момент инерции сплошного цилиндра (диска) относительно оси симметрии:
1
J mR 2
2
-тонкостенного цилиндра относительно его геометрической оси:
J mR 2
- момент инерции сплошного шара относительно любой оси, проходящей
через его центр:
2
J m R 2.
5
28. 4.5 Теорема Штейнера Момент инерции тела в том случае, когда ось вращения не проходит через центр масс, определяется по теореме
Штейнера:Момент инерции тела J относительно произвольной оси равен
сумме момента инерции тела J0 относительно оси, проходящей через центр
инерции тела параллельно данной, и произведения массы тела m на квадрат
кратчайшего расстояния между этими осями:
J 0 OZ
J O Z
29. Пример 1. Момент инерции тонкого стержня относительно оси, проходящей перпендикулярно стержню через его конец :
Пример 2. Момент инерциисплошного диска (цилиндра)
относительно оси,
совпадающей с его образующей:
30. 4.6 Кинетическая энергия и работа при вращении твердого тела. Кинетическая энергия тела при вращении вокруг неподвижной оси ОZ
будет равна сумме кинетических энергий всех его материальных точек:N
N m 2
T T i i .
i
i 1 i 1 2
Все материальные точки m
i
твердого тела вращаются
угловыми скоростями
i
с одинаковыми
Линейная скорость каждой материальной точки твердого тела равна
R
i
i
.
Кинетическая энергия вращательного движения твердого тела примет вид:
1 2N
T m R 2.
2 i 1 i i
Или:
(1)
31. В общем случае кинетическая энергия при произвольном, но плоском движении твердого тела может быть представлена в виде суммы
двух слагаемых:m 2 J 2
T 0 0
2
2
,
где первое слагаемое представляет собой кинетическую энергию материальной
точки с массой, равной массе тела и движущейся со скоростью, которую имеет
центр масс тела;
второе слагаемое представляет собой кинетическую энергию тела,
вращающегося вокруг оси, проходящей через его центр инерции.
32. Механическую работу при вращении твердого тела вокруг неподвижной оси можно вычислить, воспользовавшись тем фактом, что она
идет наприращение кинетической энергии материальных точек этого тела, то есть
A dT .
(2)
Продифференцируем выражение для кинетической энергии вращающегося
тела (1):
2
.
J z
dT d
2
d
Учтя теперь, что
J
z dt
d
J d J dt
z
z dt
M
z
dt d
,а
- элементарный угол поворота тела вокруг оси Z, придем к выражению для
механической работы:
A M d .
z
При повороте тела на конечный угол вокруг неподвижной оси для
вычисления работы необходимо проинтегрировать последнее выражение:
A A M d .
z
0
Справедливо также (см.(2)):
.
33. Физические законы, описывающие поступательное и вращательное движения т.т., аналогичны. Поэтому законы вращательного движения
т.т. можно получить иззаконов поступательного движения простой заменой одних физических величин на
другие.
Таблица аналогий поступательного и вращательного движений т.т.
F
m
p m
- сила
- масса
- момент силы
-момент
Jz
инерции
относительно данной оси
L J
- импульс
-момент импульса
dp
dL
F - основное уравнение динамики
M - основное уравнение динамики
dt
dt
n
n
N
n
,
если
закон
,
если
L
const
p i const
Fi 0
M i 0 - закон
i
i 1
i 1
i 1
i 1
сохранения
импульса
сохранения
момента импульса
m 2
T
2
A F dr
- кинетическая энергия
-механическая работа
J z 2
Tвр
2
A M d
- кинетическая энергия
- механическая работа























 physics
physics








