Similar presentations:
Механика твердого тела
1. 2.6 Механика твердого тела
Абсолютно твердое тело - тело, которое ни прикаких условиях не может деформироваться (т.е.
изменять свою форму и размеры - расстояние между
двумя соседними частицами этого тела остается
постоянным).
2. 2.6.1 Момент инерции
Моментом инерции материальной точки относительнооси
вращения
называется
скалярная
величина,
равная
J i mi ri
Моментом
инерции
2
тела
относительно данной оси
величина
(системы
n-тел)
называется скалярная
i=n
J= m i ri2
i=1
где ri - расстояние i-точки массы mi до оси,
3.
Значения J:для полого тонкостенного цилиндра радиуса
R, ось является осью симметрии цилиндра
J = mR2
для сплошного цилиндра (диска) радиуса R,
ось является осью симметрии цилиндра
mR
J=
2
2
4.
для прямого тонкого стержня длины L:
1.
ось перпендикулярна стержню и проходит через
его середину
2.
2
mL
J=
12
ось перпендикулярна стержню и проходит через
один из его концов
2
mL
J=
3
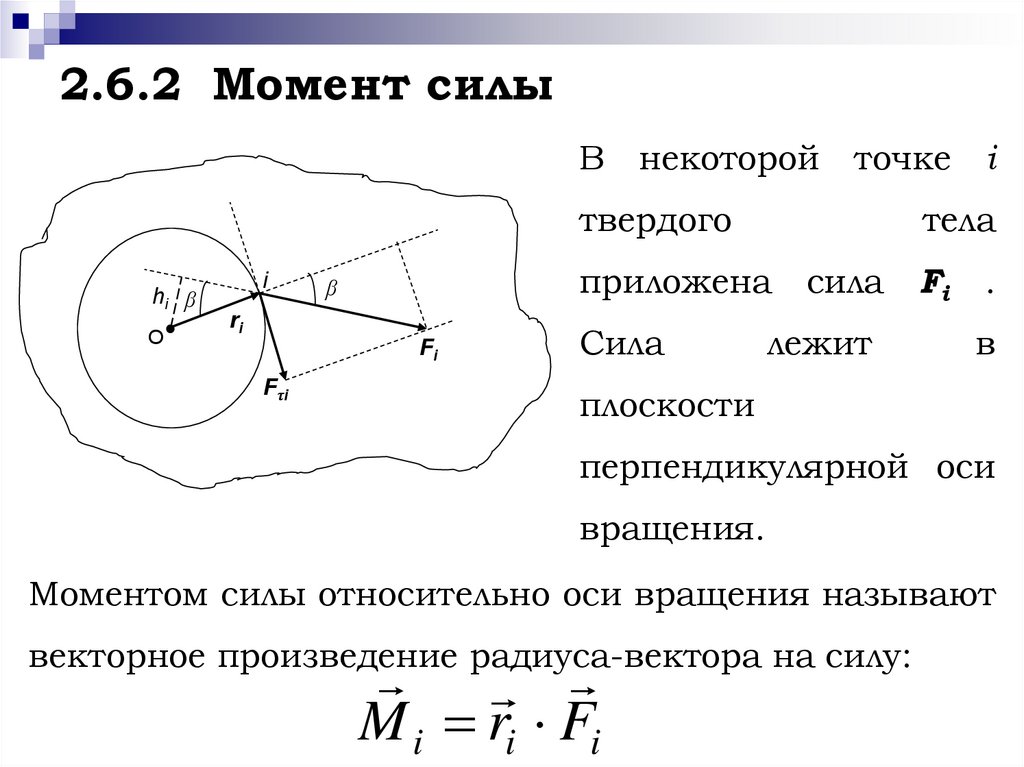
5. 2.6.2 Момент силы
Внекоторой
точке
твердого
hi β
O
i
ri
Fi
Fτi
тела
приложена
β
Сила
i
сила
лежит
Fi
.
в
плоскости
перпендикулярной оси
вращения.
Моментом силы относительно оси вращения называют
векторное произведение радиуса-вектора на силу:
M i ri Fi
6.
Раскрывая векторное произведениеM i ri Fi sin
где β – угол между векторами ri и Fi
Величина
hi ri sin
называется плечом силы.
Поэтому:
M i Fi hi
7. 2.6.3 Кинетическая энергия вращения абсолютно твердого тела
Кинетическая энергия вращения абсолютно твердоготела
вращающегося около неподвижной оси z с
угловой скоростью ω
J z
Wвр
2
2
где Jz - момент инерции тела относительно оси z.
8.
Если цилиндр скатывается с наклонной плоскостибез
скольжения,
складывается
из
то
кинетическая
энергии
энергия
поступательного
движения и энергии вращения
mv J c
Wk
2
2
2
c
2
где m - масса тела, vc - скорость центра массы
тела, Jc - момент инерции тела относительно оси,
проходящей через его центр массы, ω - угловая
скорость тела.
9. 2.6.4 Уравнение динамики вращательного движения
Уравнение динамики вращательного движения твердоготела относительно неподвижной оси z выглядит так:
d
Mz Jz
J z
dt
Если ось z совпадает с главной осью инерции, проходящей
через центр масс, то
M J
здесь J - главный момент инерции тела (момент инерции
относительно главной оси), -угловое ускорение, ω - угловая
скорость тела.








 physics
physics








