Динамика твердого тела

1. Общая физика Механика Динамика твердого тела.

2.

Лекция 7
Динамика твердого тела
Моментом инерции тела относительно оси называется
произведение массы тела на квадраты расстояния до оси:
J i mi ri2
Моментом инерции системы (тела) относительно
данной оси называется физическая величина, равная сумме
произведений масс материальных точек системы на квадраты их
расстояний до рассматриваемой оси:
n
J mi ri2
i 1
В случае непрерывного распределения масс эта сумма сводится к
интегралу по объему тела:
m
J r 2dm
0
2

3.

Тело
Положение оси
вращения
Полый
тонкостенный
цилиндр радиуса R
Ось симметрии
Сплошной цилиндр
или диск радиуса R
Ось симметрии
Стержень длиной l
Ось перпендикулярна
стержню и проходит
через его середину
Шар радиуса R
Ось проходит через
центр шара
Момент инерции
J mR 2
J
1
mR 2
2
1
ml 2
12
2
J mR 2
5
J

4.

Теорема Штейнера:
J относительно произвольной оси равен
моменту его инерции Jc относительно параллельной оси,
«момент инерции тела
проходящей через центр масс С тела, сложенному с
произведением массы т тела на квадрат расстояния а между
осями»
J JC ma 2 .
Пример.
Момент инерции длинного стержня, у которого ось симметрии
проходит через конец стержня:
2
1
1 2 1 2
l
2
J JC m
ml ml ml
12
4
3
2
4

5.

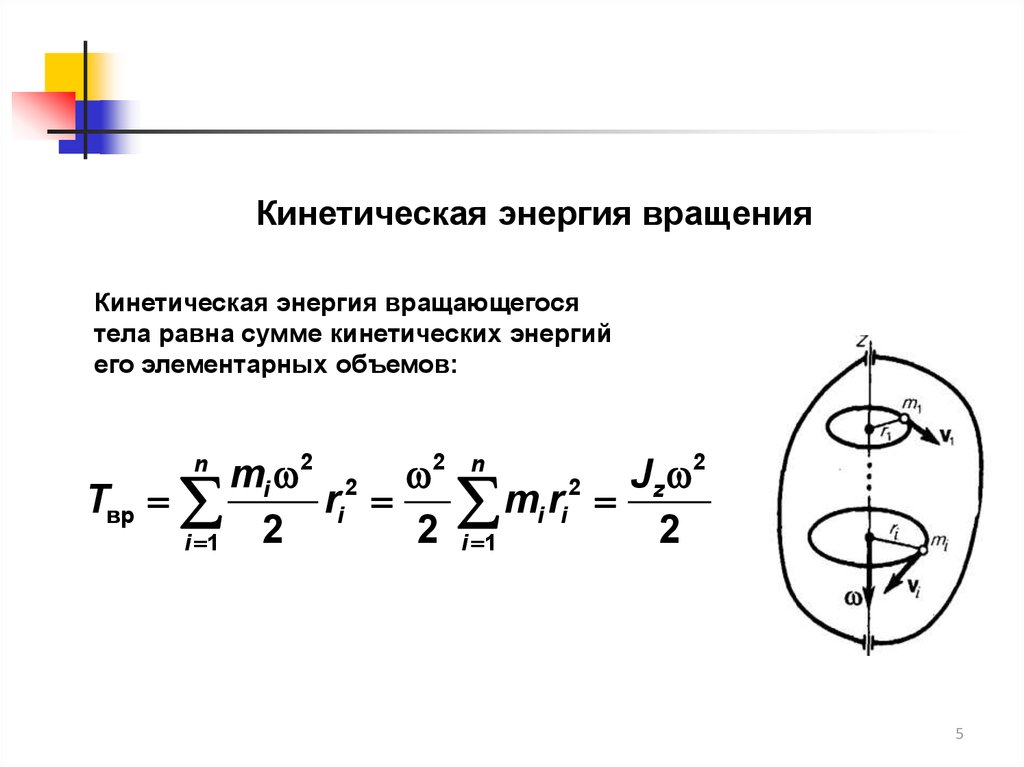
Кинетическая энергия вращения
Кинетическая энергия вращающегося
тела равна сумме кинетических энергий
его элементарных объемов:
2
mi 2 2 2 n
J
2
z
Tвр
ri
m
r
i i
2
2 i 1
2
i 1
n
5

6.

Момент инерции — мера инертности тела при вращательном
движении.
В случае плоского движения тела, например цилиндра,
скатывающегося с наклонной плоскости без скольжения, энергия
движения складывается из энергии поступательного движения и
энергии вращения:
mvC2 JC 2
T
2
2
6

7.

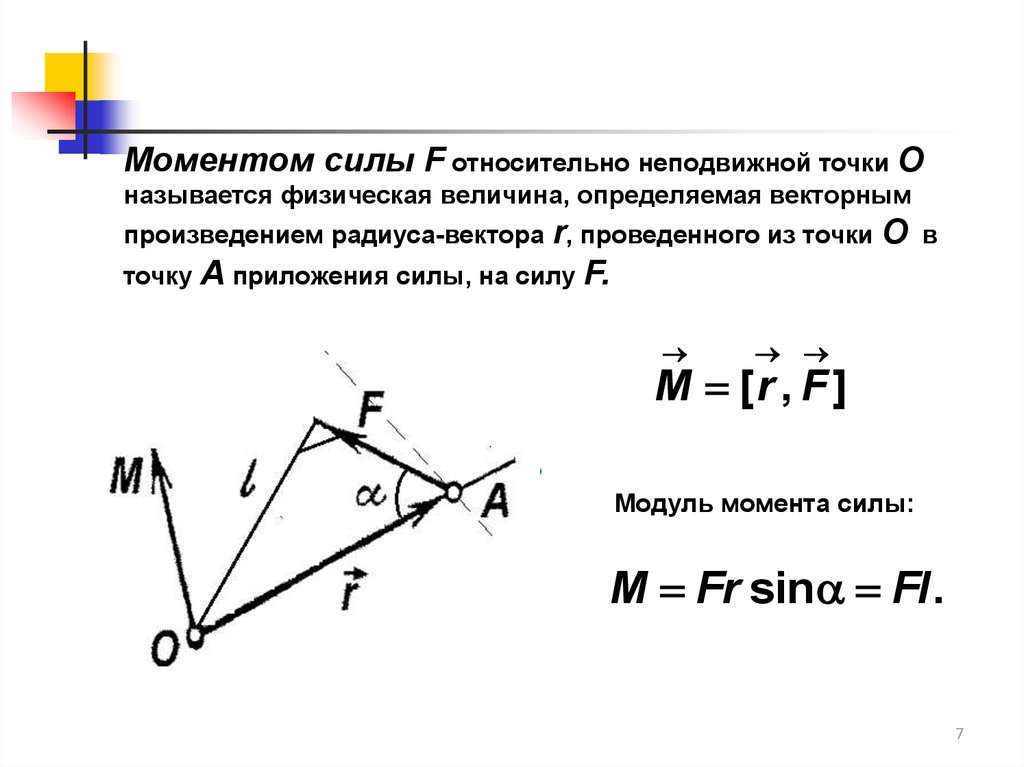
Моментом силы F относительно неподвижной точки О
называется физическая величина, определяемая векторным
произведением радиуса-вектора r, проведенного из точки
О
в
точку А приложения силы, на силу F.
M [r , F ]
Модуль момента силы:
M Fr sin Fl .
7

8.

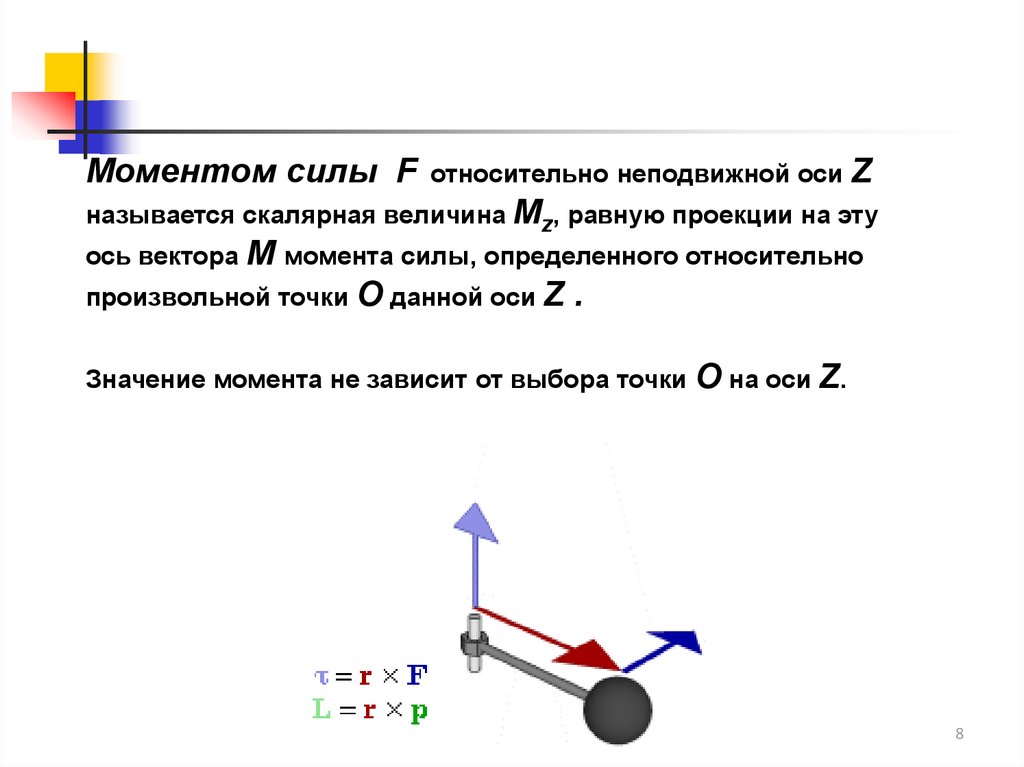
Моментом силы F
относительно неподвижной оси Z
называется скалярная величина Mz, равную проекции на эту
ось вектора M момента силы, определенного относительно
произвольной точки O данной оси Z
.
Значение момента не зависит от выбора точки
O на оси Z.
8

9.

Работа при вращении тела:
dA Mz d .
Работа при вращении тела идет на увеличение его кинетической
энергии:
J z 2
dK d
Jz d
2
Отсюда:
Mz d J z d ,
d
d
Mz
Jz
dt
dt
- уравнение динамики вращательного
движения твердого тела относительно
неподвижной оси.
9

10.

Если ось z совпадает с главной осью инерции, проходящей
через центр масс, то имеет место векторное равенство:
M J ,
– основной закон динамики вращательного движения.
J — главный момент инерции тела.
Главный момент инерции – момент инерции
относительно главной оси, проходящий через центр масс.
10

11.

Моментом импульса
материальной точки A относительно
неподвижной оси O называется
физическая величина, определяемая
векторным произведением:
L [ r , p ] [ r , mv ]
11

12.

Моментом импульса относительно неподвижной оси z
называется скалярная величина Lz, равная проекции на эту ось
вектора момента импульса, определенного относительно
произвольной точки О данной оси.
Скорость vi и импульс mivi каждой отдельной точки A тела
перпендикулярны этому радиусу, т. е. радиус является плечом
вектора mivi .
Li z mi v i ri .
12

13.

Момент импульса твердого тела относительно оси
есть сумма моментов импульса отдельных частиц (точек):
n
n
i 1
i 1
Lz mi ri2 mi ri2 J z , Lz J z .
Продифференцируем записанное уравнение по времени:
dLz
d
Jz
J z Mz ,
dt
dt
dLz
Mz .
dt
Это еще одна форма уравнения динамики вращательного
движения твердого тела относительно неподвижной оси:
«производная момента импульса твердого тела относительно
оси равна моменту сил относительно той же оси».
13

14.

Закон сохранения момента импульса:
«момент импульса замкнутой системы сохраняется, т. е. не
изменяется с течением времени».
L const
Закон сохранения момента импульса — фундаментальный закон
природы.
Он связан со свойством симметрии пространства — его
изотропностью, т. е. с инвариантностью физических законов
относительно выбора направления осей координат системы
отсчета.
Пространство называется изотропным, если
поворот системы отсчета на произвольный угол не приведет к
изменению результатов измерений.
14

15.

Соотношение основных параметров
Поступательное
движение
Масса
Вращательное
движение
m
Скорость
v
dr
dt
Ускорение
a
dv
dt
Сила
Импульс
Основное
уравнение
динамики
F
p
F ma
Момент
инерции
Угловая
скорость
Угловое
ускорение
Момент силы
Момент
импульса
Основное
уравнение
динамики
J
d
dt
d
dt
M
L
M J
15