Динамика твердого тела

1.

Кафедра физики
Динамика твердого тела
Подготовила: Тенчурина А.Р.

2. План лекции:

ПЛАН ЛЕКЦИИ:
Центр масс
Момент силы
Момент импульса
Момент инерции
Теорема Штейнера
Второй закон динамики для
вращательного движения
Закон сохранения момента импульса

3.

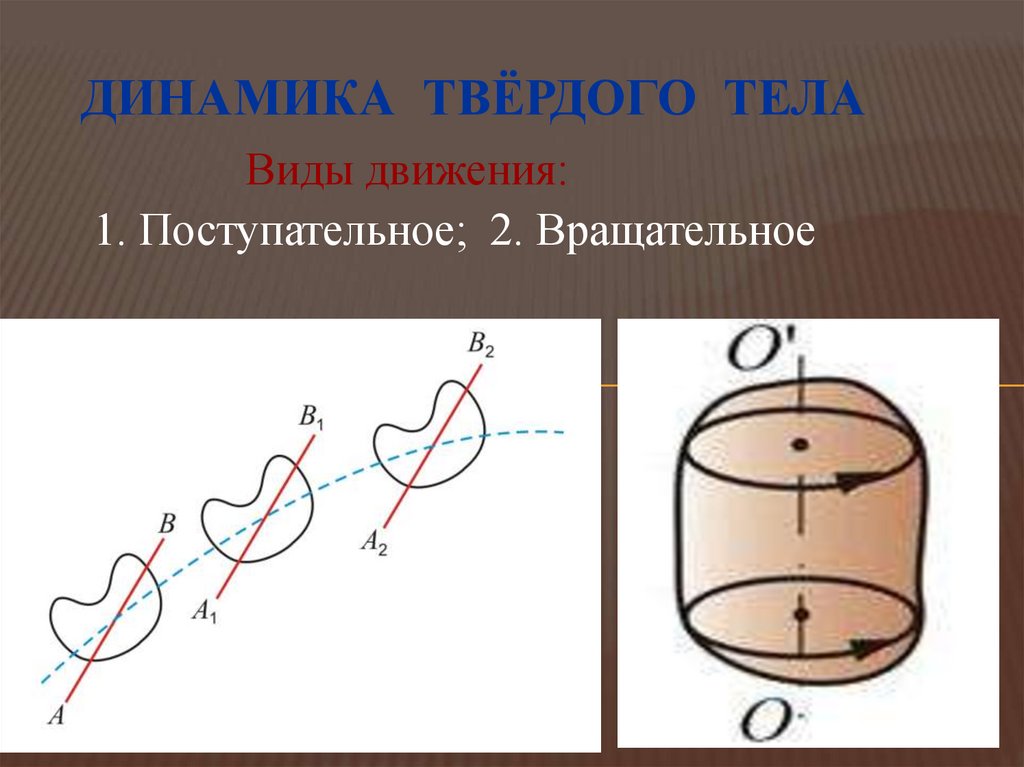
ДИНАМИКА ТВЁРДОГО ТЕЛА
Виды движения:
1. Поступательное; 2. Вращательное

4.

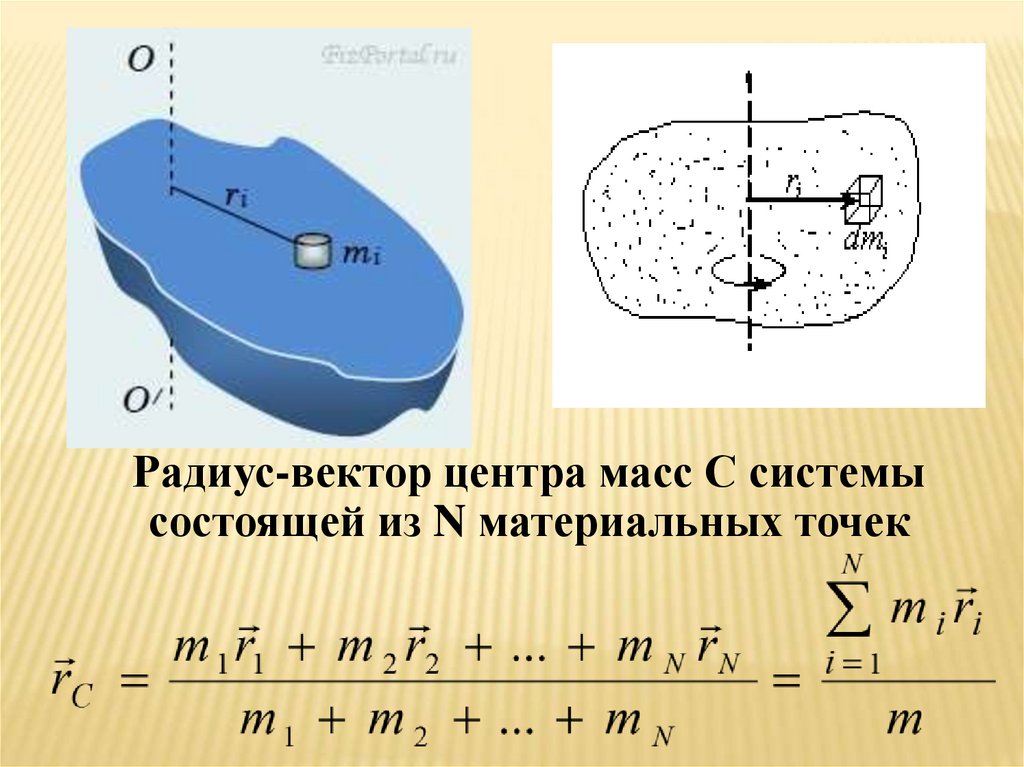
Радиус-вектор центра масс С системы
состоящей из N материальных точек

5.

N
1
rc ri mi
m i 1
mi элементарная масса
ri радиус-вектор
При
mi 0
1
rc im ri mi
mi 0 m i 1
N

6.

1
rc rdm
m
m
V
dm dV
m dm
im
dV
V 0 V
1
rc r dV
m

7. Кинетическая энергия вращающегося тела

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
ВРАЩАЮЩЕГОСЯ ТЕЛА
Кинетическая энергия – величина
аддитивная, поэтому кинетическая энергия
тела, движущегося произвольным образом,
равна сумме кинетических энергий всех n
материальных точек, на которое это тело
можно мысленно разбить:
m
K
.
2
2
n
i
i 1
i
(4.1)

8.

Если
тело
вращается
вокруг
неподвижной оси z с угловой скоростью
то линейная скорость i-й точки i ωRi
Следовательно,
ω
Iω
m R
.
2
2
2
K
2
n
2
вращ.
i 1
i
i
(4.2)
Сопоставив (4.1) и (4.2) можно
увидеть, что момент инерции тела
I–
является
мерой
инертности
при
вращательном движении. Так же как масса
m – мера инерции при поступательном
движении.

9.

В общем случае движение твердого
тела можно представить в виде суммы двух
движений – поступательного со скоростью c
и вращательного с угловой скоростью
вокруг мгновенной оси, проходящей через
центр
инерции.
Тогда
полная
кинетическая энергия этого тела:
m I
2
2
2
K
c
полн.
c
2
.
(4.3)
Здесь Ic – момент инерции относительно
мгновенной оси вращения, проходящей через
центр инерции.

10.

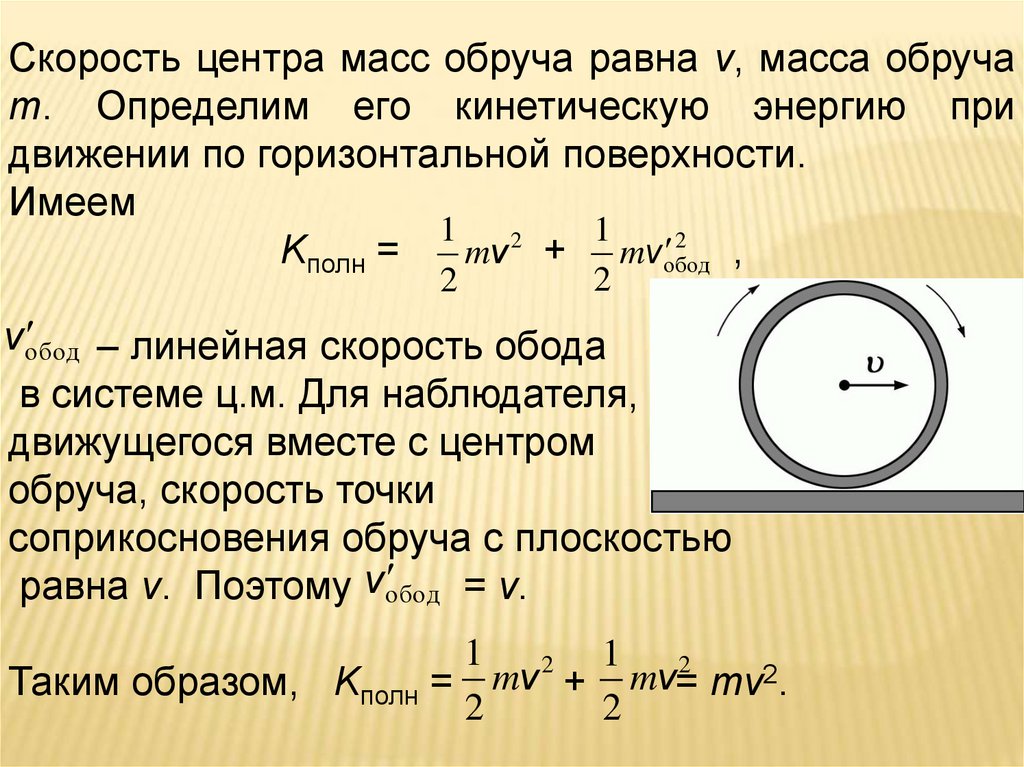
Скорость центра масс обруча равна v, масса обруча
m. Определим его кинетическую энергию при
движении по горизонтальной поверхности.
Имеем
1
1
2
2 ,
Kполн =
mv + mvобод
2
2
v обод
– линейная скорость обода
в системе ц.м. Для наблюдателя,
движущегося вместе с центром
обруча, скорость точки
соприкосновения обруча с плоскостью
равна v. Поэтому v обод
= v.
1
1
2
2
m
v
m
v
Таким образом, Kполн =
+
= mv2.
2
2

11.

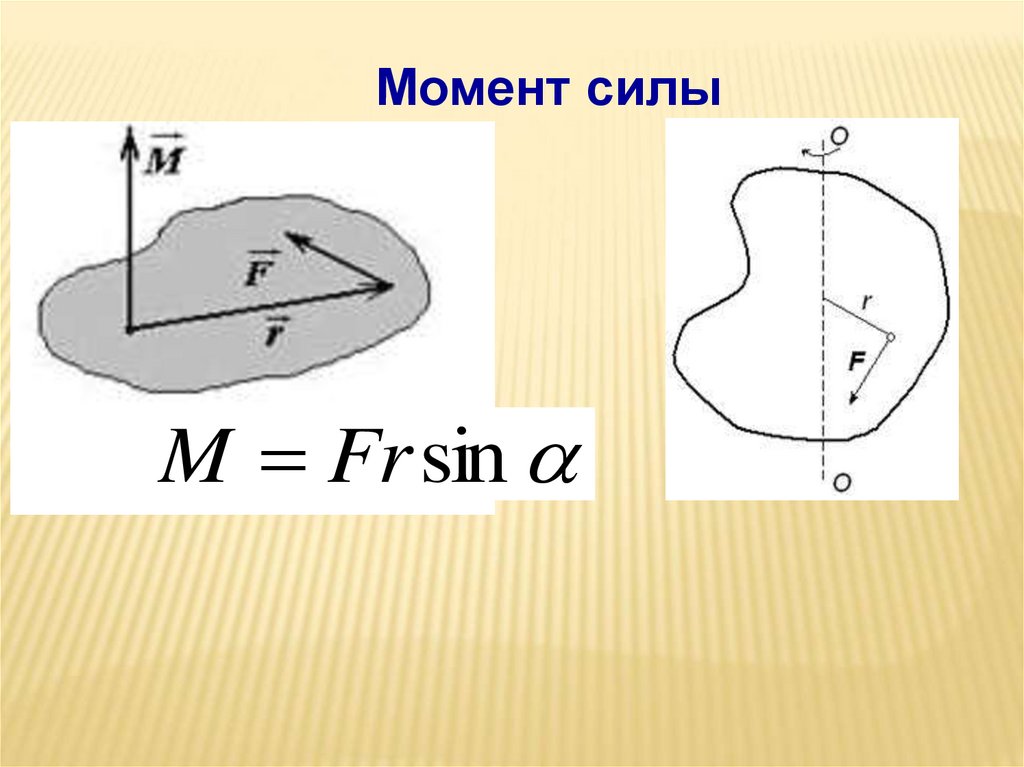
M rF
M
О
r
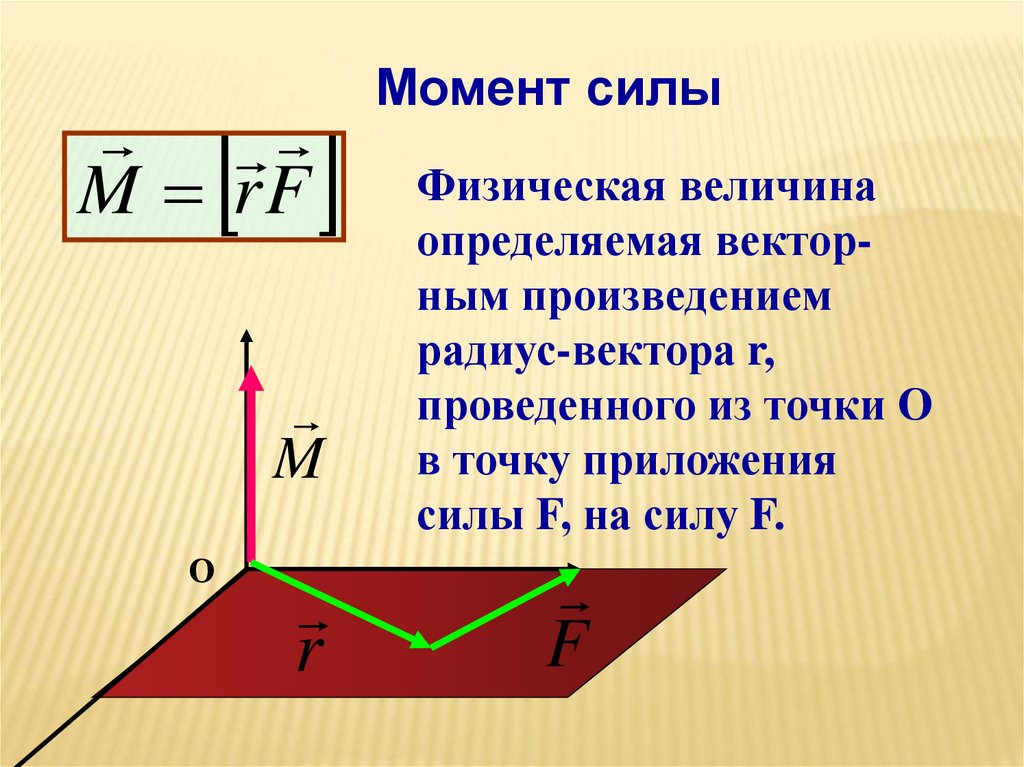
Момент силы
Физическая величина
определяемая векторным произведением
радиус-вектора r,
проведенного из точки О
в точку приложения
силы F, на силу F.
F

12.

Момент силы
M Fr sin

13.

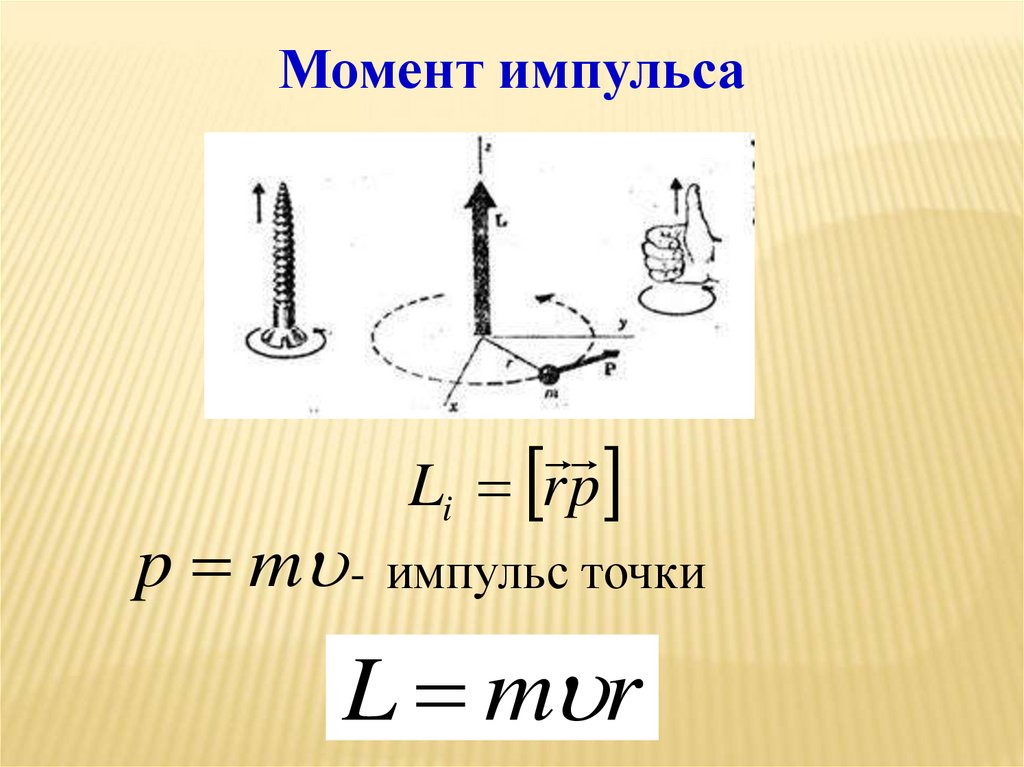
Момент импульса
Li r p
p m - импульс точки
L m r

14.

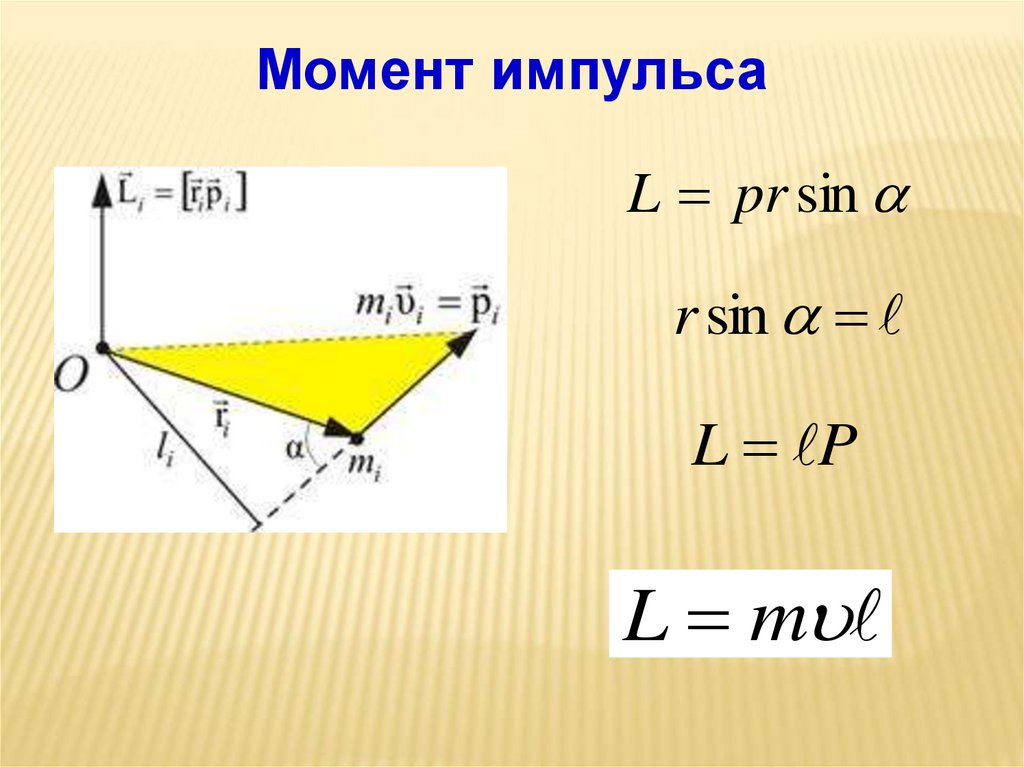
Момент импульса
L pr sin
r sin
L P
L m

15.

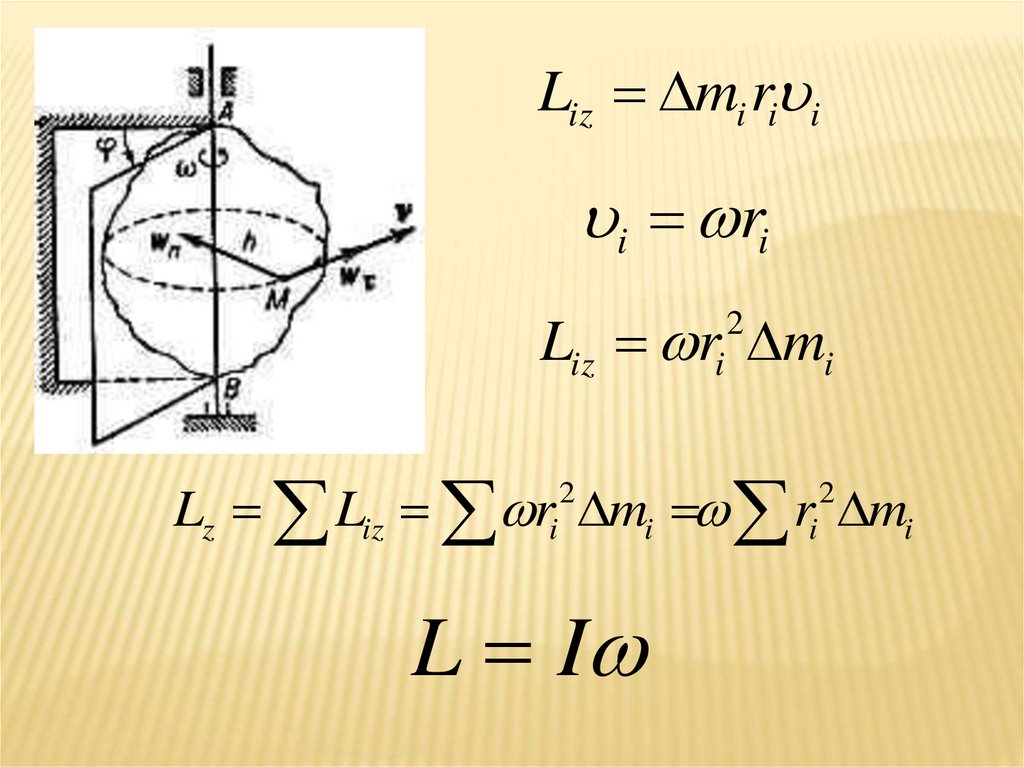
Liz mi ri i
i ri
Liz ri mi
2
Lz Liz ri mi ri mi
2
L I
2

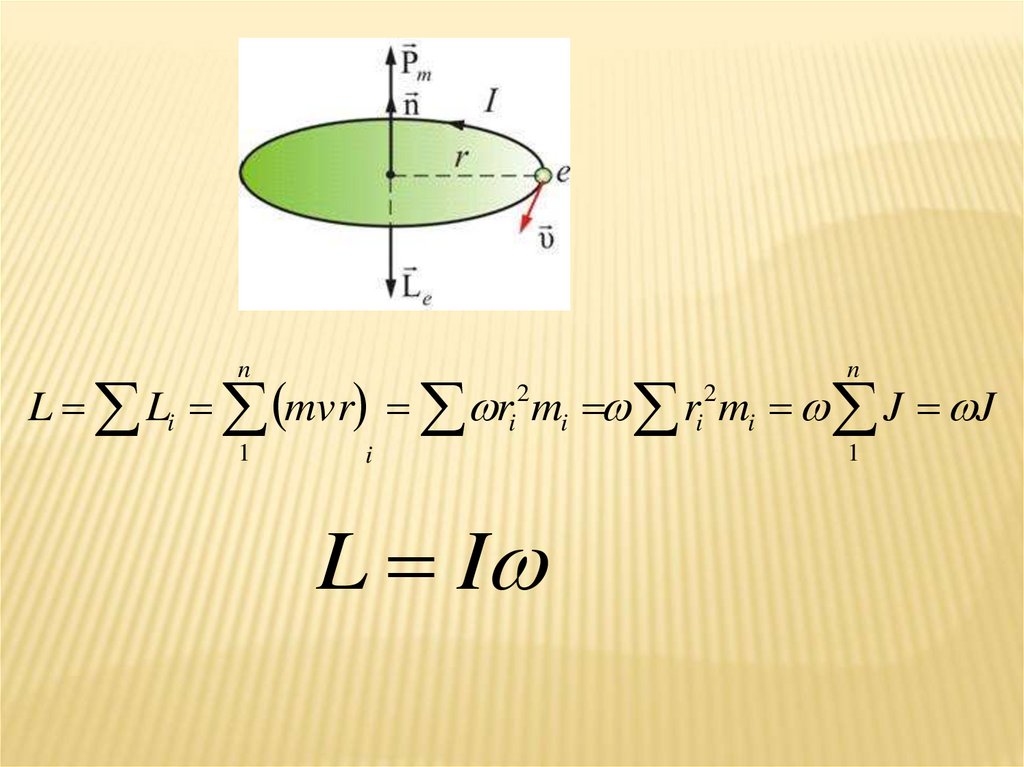
16.

n
n
L Li mvr ri 2 mi ri 2 mi J J
1
i
L I
1

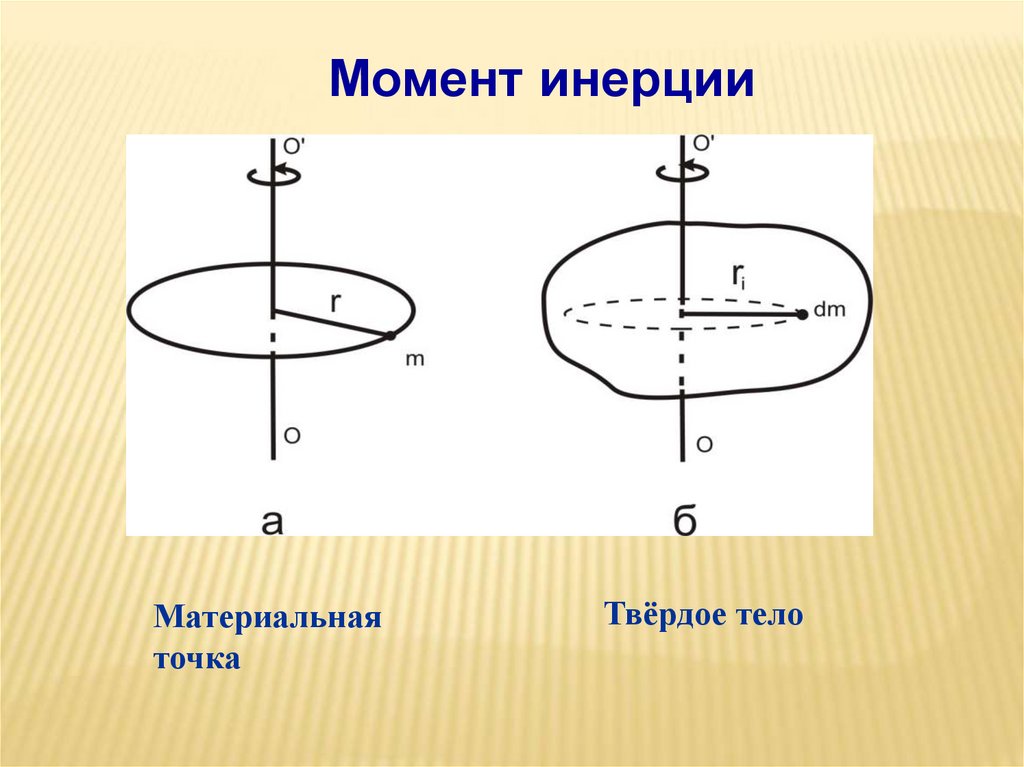
17.

Момент инерции
Материальная
точка
Твёрдое тело

18.

Момент инерции
Мера инертности тела при вращательном
движении, аналог массы при поступательном
J mr
2
J mi ri
- Материальная точка
2
- Система точек
i
J – кг м2

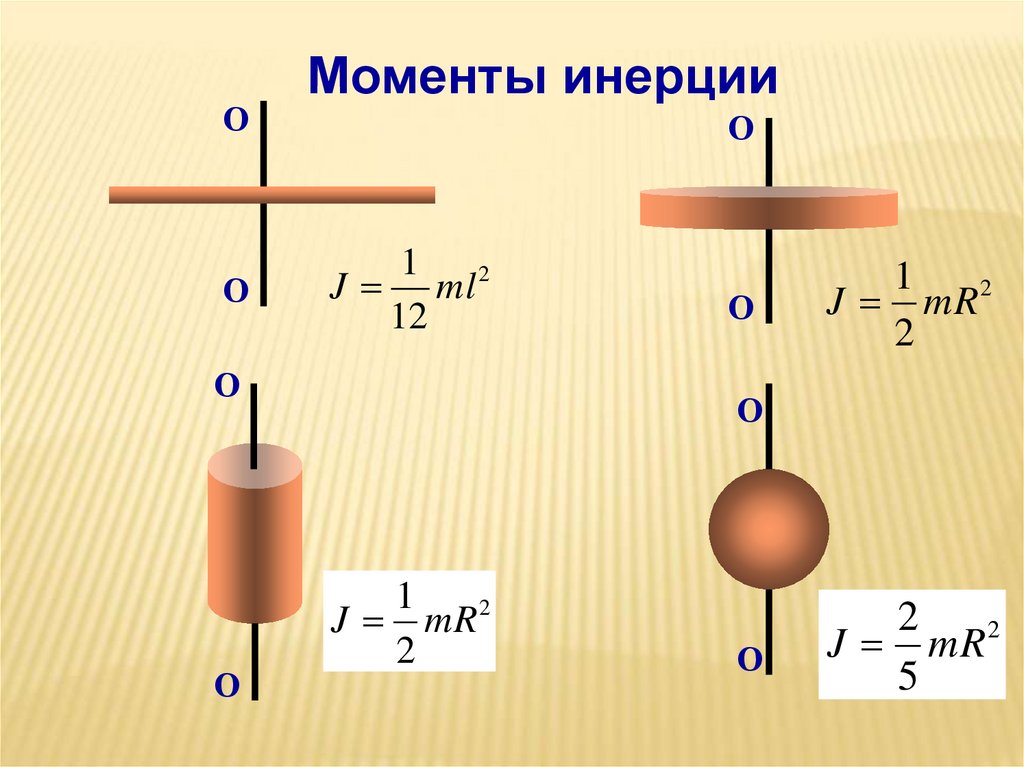
19.

О
О
Моменты инерции
О
1
J ml 2
12
О
О
О
1
J mR 2
2
О
1
2
J mR
2
О
2
2
J mR
5

20.

При вычислении момента инерции
тела, вращающегося вокруг оси, не
проходящей через центр инерции следует
пользоваться теоремой о параллельном
переносе осей или теоремой Штейнера
(Якоб Штейнер, швейцарский геометр
1796 – 1863 гг.).
I I md
c
2
(3.1)

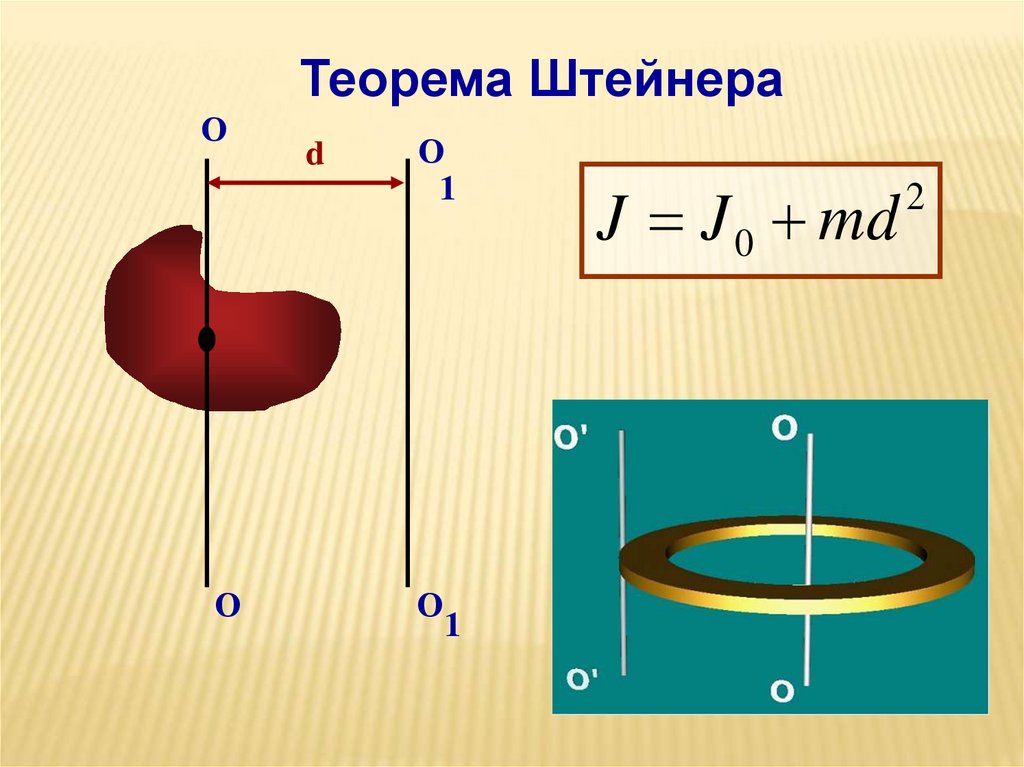
21.

Теорема Штейнера
О
О
d
О
1
О
1
J J 0 md
2

22.

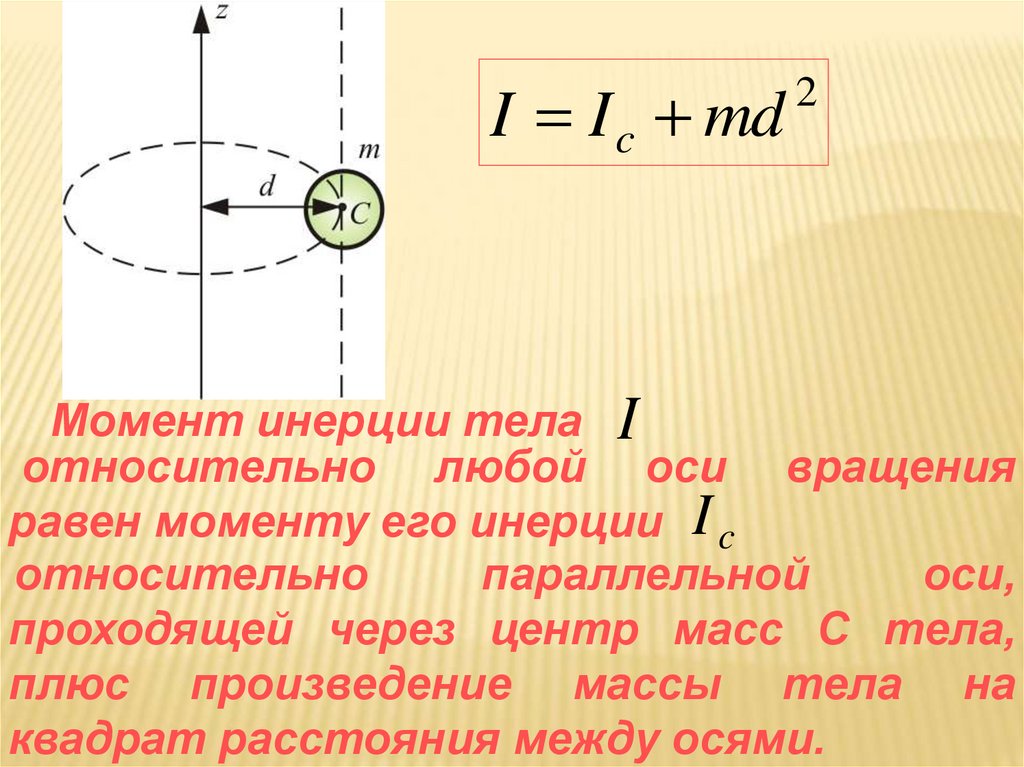
I I c md
2
Момент инерции тела I
относительно любой оси вращения
равен моменту его инерции I c
относительно
параллельной
оси,
проходящей через центр масс С тела,
плюс произведение массы тела на
квадрат расстояния между осями.

23.

Теорема Штейнера для стержня
О1
О
J J 0 md
2
1
2
J 0 ml
12
l
d
2
О1
О
1
1 2 1 2
2
J ml ml ml
12
4
3

24.

Спасибо за внимание!